DOCSLIB.ORG

Types of Waves Periodic Motion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Types of Waves Periodic Motion Lecture 19 Waves Types of waves Transverse waves Longitudinal waves Periodic Motion Superposition Standing waves Beats Waves Waves: •Transmit energy and information •Originate from: source oscillating Mechanical waves Require a medium for their transmission Involve mechanical displacement •Sound waves •Water waves (tsunami) •Earthquakes •Wave on a stretched string Non-mechanical waves Can propagate in a vacuum Electromagnetic waves Involve electric & magnetic fields •Light, • X-rays •Gamma waves, • radio waves •microwaves, etc Waves Mechanical waves •Need a source of disturbance •Medium •Mechanism with which adjacent sections of medium can influence each other Consider a stone dropped into water. Produces water waves which move away from the point of impact An object on the surface of the water nearby moves up and down and back and forth about its original position Object does not undergo any net displacement “Water wave” will move but the water itself will not be carried along. Mexican wave Waves Transverse and Longitudinal waves Transverse Waves Particles of the disturbed medium through which the wave passes move in a direction perpendicular to the direction of wave propagation Wave on a stretched string Electromagnetic waves •Light, • X-rays etc Longitudinal Waves Particles of the disturbed medium move back and forth in a direction along the direction of wave propagation. Mechanical waves •Sound waves Waves Transverse waves Pulse (wave) moves left to right Particles of rope move in a direction perpendicular to the direction of the wave Rope never moves in the direction of the wave Energy and not matter is transported by the wave Waves Transverse and Longitudinal waves Transverse Waves Motion of disturbed medium is in a direction perpendicular to the direction of wave propagation Longitudinal Waves Particles of the disturbed medium move in a direction along the direction of wave propagation. Waves Vibrational motion Object attached to spring. Spring compressed or stretched a small distance (x) and then released ; a force (Fr) is exerted on the object by the spring Motion of mass as a function of time traces out a sine wave Displacement m Fr x m time x Fr m Net restoring force F r Fxr proportional to x: object undergoes simple harmonic motion Fr kx Waves Hooke’s law Not only applies to springs Fr kx Waves Object vibrating with single frequency Single frequency wave characteristics Displacement versus time (or distance) crest l amplitude Time or distance Displacement Trough l Wavelength : Distance between two successive identical points on the wave (λ) Amplitude : Max height of a crest or depth of a trough relative to the normal level Wave Velocity : Velocity at which the wave s crests move. v s vt t l vT 1 l v vf l f Waves Sound A plucked string will vibrate at its natural frequency and alternately compresses and rarefies the air alongside it. rarefaction compression Density of Air of Density Compressed air [increased pressure] Rarefied air [reduced pressure] Air molecules move away from high pressure region >>>>>> setting up longitudinal wave organised vibrations of air molecules>> sound Waves Sound waves-(variation in air pressure) can cause objects to oscillate Example: ear drum is forced to vibrate in response to the air pressure variation Waves Wave characteristics Frequency of waves • Frequency (f) of a wave is independent of the medium through which the wave travels. –it is determined by the frequency of the oscillator that is the source of the waves. Speed of waves •The speed of the wave is dependent on the characteristics of the medium through which the wave is traveling. Wavelength •The wavelength (l) is a function of both the oscillator frequency and the speed (v) of the wave such that vf l Waves Superposition Two or more waves travelling through same part of medium at the same time What happens? Adding waves sum of the disturbances of the combined waves If amplitude increases: constructive interference If amplitude decreases: destructive interference Vocal sounds .combination of waves of different frequencies Voice individually recognisable Waves Superposition Simple case: Addition of two waves with same wavelength and amplitude In step: Added, crest to crest (trough to trough) wave 1 wave 2 time displacement resultant Out of step: Added, crest to trough wave 1 wave 2 resultant Waves Standing waves Two waves (same frequency) travelling in opposite directions Waves reflected back from a fixed position Fundamental 1st Overtone 2nd Overtone 3rd Overtone Nodes; positions of no displacement Antinodes; positions of maximum displacement Distance between successive nodes (antinodes) = l Applications 2 Microwave ovens Musical instruments Waves Standing waves Fundamental 1st Overtone 2nd Overtone 3rd Overtone String held tightly at both ends Only certain modes of vibration allowed Only certain wavelengths allowed Standing wave must have node at either end Length of string may be changed to get other wavelengths Example: guitar fingering Changing the vibrating length Standing waves: organ pipes Waves Waves on a stretched string Consider a vibrating string; Wave speed is a function of •tension of the string •Mass per unit length T Wave speed v mL/ T is the tension m is the mass of the string L is the length of the string Waves Example What is the frequency of the fundamental mode of vibration of a wire of length 400mm and mass 3.00 g with a tension of 300N. T Wave speed vfl mL/ 300Nm (400 103 ) v 3 103 kg v(4 104 ) m 2 s 2 200 ms 1 l= 2L v200 ms1 f 250 Hz 2Lm 2 0.4 vf l Waves Superposition Simple case: Addition of two waves with same frequency and amplitude Beats If the two waves interfering have slightly different frequencies (wavelengths), beats occur. In step (in phase) In step (in phase) Out of step (out of phase) Waves Beats If the two waves interfering have slightly different frequencies (wavelengths), beats occur. Wave 1 Wave 2 resultant Waves get in and out of step as time progresses Result- • constructive and destructive interference occurs alternately •Amplitude changes periodically at the beat frequency Beat frequency = fb = f1-f2 Absolute value: beat frequency always positive Waves Beats fb = f1-f2 If frequency difference = zero No beats occur Wave 1 Wave 2 resultant Waves Beats Beats can happen with any type of waves Sound waves Beats perceived as a modulated sound: loudness varies periodically at the beat frequency Application Accurate determination of frequency Example Piano tuning Adjust tension in wire and listen for beats between it and a tuning fork of known frequency The two frequencies are equal when the beats cease. Easier to determine than when listening to individual sounds of nearly equal frequencies f1 = 264Hz f2 = 266 Hz Beat frequency 2Hz Waves Multiple frequencies of different amplitudes added together •complex resultant Sound waves Resultant tone •Particular musical instrument •Person’s voice Waves Question Tuning a guitar by comparing sound of the string with that of a standard tuning fork. A beat frequency of 5 Hz is heard when both sounds are present. The guitar string is tighten the and the beat frequency rises to 8Hz. To tune the string exactly to the frequency of the tuning fork what should be done? • a) continue to tighten the string • b) loosen the string • c) it is impossible to determine Resonance Most objects have a natural frequency: Determined by • size • shape •composition System is in resonance if the frequency of the driving force equals the natural frequency of the system Resonance: examples child being pushed on a swing. Opera singer -breaking glass Voice Air passages of the mouth, larynx and nasal cavity together form an acoustic resonator. Voiced sound depend on •resonant frequencies of the total system ------depends on system’s volume and shape Resonance: examples Tacoma narrows Bridge, WashingtonElectrical State, Resonance: US, 1940Example: Tuning in radio station Adjust resonant frequency of the electrical circuit to the broadcast frequency of the radio station To “pick up” signal Waves Question Frequency is constant. Its is determined by the source of the wave. 1 Since f Period in constant period Propagation speed depends on properties of string T vfl mL/.
Load more

Recommended publications
  • Computational Characterization of the Wave Propagation Behaviour of Multi-Stable Periodic Cellular Materials∗
    Computational Characterization of the Wave Propagation Behaviour of Multi-Stable Periodic Cellular Materials∗ Camilo Valencia1, David Restrepo2,4, Nilesh D. Mankame3, Pablo D. Zavattieri 2y , and Juan Gomez 1z 1Civil Engineering Department, Universidad EAFIT, Medell´ın,050022, Colombia 2Lyles School of Civil Engineering, Purdue University, West Lafayette, IN 47907, USA 3Vehicle Systems Research Laboratory, General Motors Global Research & Development, Warren, MI 48092, USA. 4Department of Mechanical Engineering, The University of Texas at San Antonio, San Antonio, TX 78249, USA Abstract In this work, we present a computational analysis of the planar wave propagation behavior of a one-dimensional periodic multi-stable cellular material. Wave propagation in these ma- terials is interesting because they combine the ability of periodic cellular materials to exhibit stop and pass bands with the ability to dissipate energy through cell-level elastic instabilities. Here, we use Bloch periodic boundary conditions to compute the dispersion curves and in- troduce a new approach for computing wide band directionality plots. Also, we deconstruct the wave propagation behavior of this material to identify the contributions from its various structural elements by progressively building the unit cell, structural element by element, from a simple, homogeneous, isotropic primitive. Direct integration time domain analyses of a representative volume element at a few salient frequencies in the stop and pass bands are used to confirm the existence of partial band gaps in the response of the cellular material. Insights gained from the above analyses are then used to explore modifications of the unit cell that allow the user to tune the band gaps in the response of the material.
    [Show full text]
  • Vector Wave Propagation Method Ein Beitrag Zum Elektromagnetischen Optikrechnen
    Vector Wave Propagation Method Ein Beitrag zum elektromagnetischen Optikrechnen Inauguraldissertation zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften der Universitat¨ Mannheim vorgelegt von Dipl.-Inf. Matthias Wilhelm Fertig aus Mannheim Mannheim, 2011 Dekan: Prof. Dr.-Ing. Wolfgang Effelsberg Universitat¨ Mannheim Referent: Prof. Dr. rer. nat. Karl-Heinz Brenner Universitat¨ Heidelberg Korreferent: Prof. Dr.-Ing. Elmar Griese Universitat¨ Siegen Tag der mundlichen¨ Prufung:¨ 18. Marz¨ 2011 Abstract Based on the Rayleigh-Sommerfeld diffraction integral and the scalar Wave Propagation Method (WPM), the Vector Wave Propagation Method (VWPM) is introduced in the thesis. It provides a full vectorial and three-dimensional treatment of electromagnetic fields over the full range of spatial frequen- cies. A model for evanescent modes from [1] is utilized and eligible config- urations of the complex propagation vector are identified to calculate total internal reflection, evanescent coupling and to maintain the conservation law. The unidirectional VWPM is extended to bidirectional propagation of vectorial three-dimensional electromagnetic fields. Totally internal re- flected waves and evanescent waves are derived from complex Fresnel coefficients and the complex propagation vector. Due to the superposition of locally deformed plane waves, the runtime of the WPM is higher than the runtime of the BPM and therefore an efficient parallel algorithm is de- sirable. A parallel algorithm with a time-complexity that scales linear with the number of threads is presented. The parallel algorithm contains a mini- mum sequence of non-parallel code which possesses a time complexity of the one- or two-dimensional Fast Fourier Transformation. The VWPM and the multithreaded VWPM utilize the vectorial version of the Plane Wave Decomposition (PWD) in homogeneous medium without loss of accuracy to further increase the simulation speed.
    [Show full text]
  • The Science of String Instruments
    The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D.
    [Show full text]
  • Standing Waves and Sound
    Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go.
    [Show full text]
  • Superconducting Metamaterials for Waveguide Quantum Electrodynamics
    ARTICLE DOI: 10.1038/s41467-018-06142-z OPEN Superconducting metamaterials for waveguide quantum electrodynamics Mohammad Mirhosseini1,2,3, Eunjong Kim1,2,3, Vinicius S. Ferreira1,2,3, Mahmoud Kalaee1,2,3, Alp Sipahigil 1,2,3, Andrew J. Keller1,2,3 & Oskar Painter1,2,3 Embedding tunable quantum emitters in a photonic bandgap structure enables control of dissipative and dispersive interactions between emitters and their photonic bath. Operation in 1234567890():,; the transmission band, outside the gap, allows for studying waveguide quantum electro- dynamics in the slow-light regime. Alternatively, tuning the emitter into the bandgap results in finite-range emitter–emitter interactions via bound photonic states. Here, we couple a transmon qubit to a superconducting metamaterial with a deep sub-wavelength lattice constant (λ/60). The metamaterial is formed by periodically loading a transmission line with compact, low-loss, low-disorder lumped-element microwave resonators. Tuning the qubit frequency in the vicinity of a band-edge with a group index of ng = 450, we observe an anomalous Lamb shift of −28 MHz accompanied by a 24-fold enhancement in the qubit lifetime. In addition, we demonstrate selective enhancement and inhibition of spontaneous emission of different transmon transitions, which provide simultaneous access to short-lived radiatively damped and long-lived metastable qubit states. 1 Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA 91125, USA. 2 Thomas J. Watson, Sr., Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA 91125, USA. 3 Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA 91125, USA. Correspondence and requests for materials should be addressed to O.P.
    [Show full text]
  • Electromagnetism As Quantum Physics
    Electromagnetism as Quantum Physics Charles T. Sebens California Institute of Technology May 29, 2019 arXiv v.3 The published version of this paper appears in Foundations of Physics, 49(4) (2019), 365-389. https://doi.org/10.1007/s10701-019-00253-3 Abstract One can interpret the Dirac equation either as giving the dynamics for a classical field or a quantum wave function. Here I examine whether Maxwell's equations, which are standardly interpreted as giving the dynamics for the classical electromagnetic field, can alternatively be interpreted as giving the dynamics for the photon's quantum wave function. I explain why this quantum interpretation would only be viable if the electromagnetic field were sufficiently weak, then motivate a particular approach to introducing a wave function for the photon (following Good, 1957). This wave function ultimately turns out to be unsatisfactory because the probabilities derived from it do not always transform properly under Lorentz transformations. The fact that such a quantum interpretation of Maxwell's equations is unsatisfactory suggests that the electromagnetic field is more fundamental than the photon. Contents 1 Introduction2 arXiv:1902.01930v3 [quant-ph] 29 May 2019 2 The Weber Vector5 3 The Electromagnetic Field of a Single Photon7 4 The Photon Wave Function 11 5 Lorentz Transformations 14 6 Conclusion 22 1 1 Introduction Electromagnetism was a theory ahead of its time. It held within it the seeds of special relativity. Einstein discovered the special theory of relativity by studying the laws of electromagnetism, laws which were already relativistic.1 There are hints that electromagnetism may also have held within it the seeds of quantum mechanics, though quantum mechanics was not discovered by cultivating those seeds.
    [Show full text]
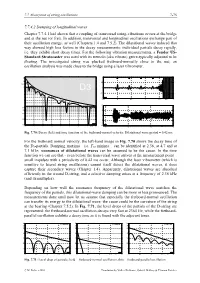
  • 7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
    7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples).
    [Show full text]
  • Giant Slinky: Quantitative Exhibit Activity
    Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position.
    [Show full text]
  • Matter Wave Speckle Observed in an Out-Of-Equilibrium Quantum Fluid
    Matter wave speckle observed in an out-of-equilibrium quantum fluid Pedro E. S. Tavaresa, Amilson R. Fritscha, Gustavo D. Tellesa, Mahir S. Husseinb, Franc¸ois Impensc, Robin Kaiserd, and Vanderlei S. Bagnatoa,1 aInstituto de F´ısica de Sao˜ Carlos, Universidade de Sao˜ Paulo, 13560-970 Sao˜ Carlos, SP, Brazil; bDepartamento de F´ısica, Instituto Tecnologico´ de Aeronautica,´ 12.228-900 Sao˜ Jose´ dos Campos, SP, Brazil; cInstituto de F´ısica, Universidade Federal do Rio de Janeiro, 21941-972 Rio de Janeiro, RJ, Brazil; and dUniversite´ Nice Sophia Antipolis, Institut Non-Lineaire´ de Nice, CNRS UMR 7335, F-06560 Valbonne, France Contributed by Vanderlei Bagnato, October 16, 2017 (sent for review August 14, 2017; reviewed by Alexander Fetter, Nikolaos P. Proukakis, and Marlan O. Scully) We report the results of the direct comparison of a freely expanding turbulent Bose–Einstein condensate and a propagating optical speckle pattern. We found remarkably similar statistical properties underlying the spatial propagation of both phenomena. The cal- culated second-order correlation together with the typical correlation length of each system is used to compare and substantiate our observations. We believe that the close analogy existing between an expanding turbulent quantum gas and a traveling optical speckle might burgeon into an exciting research field investigating disordered quantum matter. matter–wave j speckle j quantum gas j turbulence oherent matter–wave systems such as a Bose–Einstein condensate (BEC) or atom lasers and atom optics are reality and relevant Cresearch fields. The spatial propagation of coherent matter waves has been an interesting topic for many theoretical (1–3) and experimental studies (4–7).
    [Show full text]
  • Woods for Wooden Musical Instruments S
    ISMA 2014, Le Mans, France Woods for Wooden Musical Instruments S. Yoshikawaa and C. Walthamb aKyushu University, Graduate School of Design, 4-9-1 Shiobaru, Minami-ku, 815-8540 Fukuoka, Japan bUniversity of British Columbia, Dept of Physics & Astronomy, 6224 Agricultural Road, Vancouver, BC, Canada V6T 1Z1 [email protected] 281 ISMA 2014, Le Mans, France In spite of recent advances in materials science, wood remains the preferred construction material for musical instruments worldwide. Some distinguishing features of woods (light weight, intermediate quality factor, etc.) are easily noticed if we compare material properties between woods, a plastic (acrylic), and a metal (aluminum). Woods common in musical instruments (strings, woodwinds, and percussions) are typically (with notable exceptions) softwoods (e.g. Sitka spruce) as tone woods for soundboards, hardwoods (e.g. amboyna) as frame woods for backboards, and monocots (e.g. bamboo) as bore woods for woodwind bodies. Moreover, if we consider the radiation characteristics of tap tones from sample plates of Sitka spruce, maple, and aluminum, a large difference is observed above around 2 kHz that is attributed to the relative strength of shear and bending deformations in flexural vibrations. This shear effect causes an appreciable increase in the loss factor at higher frequencies. The stronger shear effect in Sitka spruce than in maple and aluminum seems to be relevant to soundboards because its low-pass filter effect with a cutoff frequency of about 2 kHz tends to lend the radiated sound a desired softness. A classification diagram of traditional woods based on an anti-vibration parameter (density ρ/sound speed c) and transmission parameter cQ is proposed.
    [Show full text]
  • A Photomechanics Study of Wave Propagation John Barclay Ligon Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1971 A photomechanics study of wave propagation John Barclay Ligon Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Applied Mechanics Commons Recommended Citation Ligon, John Barclay, "A photomechanics study of wave propagation " (1971). Retrospective Theses and Dissertations. 4556. https://lib.dr.iastate.edu/rtd/4556 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. 72-12,567 LIGON, John Barclay, 1940- A PHOTOMECHANICS STUDY OF WAVE PROPAGATION. Iowa State University, Ph.D., 1971 Engineering Mechanics University Microfilms. A XEROX Company, Ann Arbor. Michigan THIS DISSERTATION HAS BEEN MICROFILMED EXACTLY AS RECEIVED A photomechanics study of wave propagation John Barclay Ligon A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject; Engineering Mechanics Approved Signature was redacted for privacy. Signature was redacted for privacy. Signature was redacted for privacy. For the Graduate College Iowa State University Ames, Iowa 1971 PLEASE NOTE; Some pages have indistinct print.
    [Show full text]
  • 1 the Principle of Wave–Particle Duality: an Overview
    3 1 The Principle of Wave–Particle Duality: An Overview 1.1 Introduction In the year 1900, physics entered a period of deep crisis as a number of peculiar phenomena, for which no classical explanation was possible, began to appear one after the other, starting with the famous problem of blackbody radiation. By 1923, when the “dust had settled,” it became apparent that these peculiarities had a common explanation. They revealed a novel fundamental principle of nature that wascompletelyatoddswiththeframeworkofclassicalphysics:thecelebrated principle of wave–particle duality, which can be phrased as follows. The principle of wave–particle duality: All physical entities have a dual character; they are waves and particles at the same time. Everything we used to regard as being exclusively a wave has, at the same time, a corpuscular character, while everything we thought of as strictly a particle behaves also as a wave. The relations between these two classically irreconcilable points of view—particle versus wave—are , h, E = hf p = (1.1) or, equivalently, E h f = ,= . (1.2) h p In expressions (1.1) we start off with what we traditionally considered to be solely a wave—an electromagnetic (EM) wave, for example—and we associate its wave characteristics f and (frequency and wavelength) with the corpuscular charac- teristics E and p (energy and momentum) of the corresponding particle. Conversely, in expressions (1.2), we begin with what we once regarded as purely a particle—say, an electron—and we associate its corpuscular characteristics E and p with the wave characteristics f and of the corresponding wave.
    [Show full text]