DOCSLIB.ORG

Chapter 16 Wave Motion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 16 Wave Motion Chapter 16 Wave Motion CHAPTER OUTLINE 16.1 Propagation of a Disturbance 16.2 Sinusoidal Waves 16.3 The Speed of Waves on Strings 16.4 Reflection and Transmission 16.5 Rate of Energy Transfer by Sinusoidal Waves on Strings 16.6 The Linear Wave Equation L The rich sound of a piano is due to waves on strings that are under tension. Many such strings can be seen in this photograph. Waves also travel on the soundboard, which is visible below the strings. In this chapter, we study the fundamental principles of wave phenomena. (Kathy Ferguson Johnson/PhotoEdit/PictureQuest) 486 Most of us experienced waves as children when we dropped a pebble into a pond. At the point where the pebble hits the water’s surface, waves are created. These waves move outward from the creation point in expanding circles until they reach the shore. If you were to examine carefully the motion of a beach ball floating on the disturbed water, you would see that the ball moves vertically and horizontally about its original position but does not undergo any net displacement away from or toward the point where the pebble hit the water. The small elements of water in contact with the beach ball, as well as all the other water elements on the pond’s surface, behave in the same way. That is, the water wave moves from the point of origin to the shore, but the water is not carried with it. The world is full of waves, the two main types being mechanical waves and electromag- netic waves. In the case of mechanical waves, some physical medium is being dis- turbed—in our pebble and beach ball example, elements of water are disturbed. Elec- tromagnetic waves do not require a medium to propagate; some examples of electromagnetic waves are visible light, radio waves, television signals, and x-rays. Here, in this part of the book, we study only mechanical waves. The wave concept is abstract. When we observe what we call a water wave, what we see is a rearrangement of the water’s surface. Without the water, there would be no wave. A wave traveling on a string would not exist without the string. Sound waves could not travel from one point to another if there were no air molecules between the two points. With mechanical waves, what we interpret as a wave corresponds to the propagation of a disturbance through a medium. Considering further the beach ball floating on the water, note that we have caused the ball to move at one point in the water by dropping a pebble at another location. The ball has gained kinetic energy from our action, so energy must have transferred from the point at which we drop the pebble to the position of the ball. This is a central feature of wave motion—energy is transferred over a distance, but matter is not. All waves carry energy, but the amount of energy transmitted through a medium and the mechanism responsible for that transport of energy differ from case to case. For instance, the power of ocean waves during a storm is much greater than the power of sound waves generated by a single human voice. 16.1 Propagation of a Disturbance In the introduction, we alluded to the essence of wave motion—the transfer of energy through space without the accompanying transfer of matter. In the list of energy transfer mechanisms in Chapter 7, two mechanisms depend on waves—mechanical waves and electromagnetic radiation. By contrast, in another mechanism—matter transfer—the energy transfer is accompanied by a movement of matter through space. All mechanical waves require (1) some source of disturbance, (2) a medium that can be disturbed, and (3) some physical mechanism through which elements of the medium can influence each other. One way to demonstrate wave 487 488 CHAPTER 16 • Wave Motion motion is to flick one end of a long rope that is under tension and has its opposite end fixed, as shown in Figure 16.1. In this manner, a single bump (called a pulse) is formed and travels along the rope with a definite speed. Figure 16.1 represents four consecu- tive “snapshots” of the creation and propagation of the traveling pulse. The rope is the medium through which the pulse travels. The pulse has a definite height and a definite speed of propagation along the medium (the rope). As we shall see later, the proper- ties of this particular medium that determine the speed of the disturbance are the ten- sion in the rope and its mass per unit length. The shape of the pulse changes very little as it travels along the rope.1 We shall first focus our attention on a pulse traveling through a medium. Once we have explored the behavior of a pulse, we will then turn our attention to a wave, which is a periodic disturbance traveling through a medium. We created a pulse on our rope by flicking the end of the rope once, as in Figure 16.1. If we were to move the end of the rope up and down repeatedly, we would create a traveling wave, which has characteris- tics that a pulse does not have. We shall explore these characteristics in Section 16.2. As the pulse in Figure 16.1 travels, each disturbed element of the rope moves in a Figure 16.1 A pulse traveling direction perpendicular to the direction of propagation. Figure 16.2 illustrates this point down a stretched rope. The shape for one particular element, labeled P. Note that no part of the rope ever moves in the of the pulse is approximately un- direction of the propagation. changed as it travels along the rope. A traveling wave or pulse that causes the elements of the disturbed medium to move perpendicular to the direction of propagation is called a transverse wave. P Compare this with another type of pulse—one moving down a long, stretched spring, as shown in Figure 16.3. The left end of the spring is pushed briefly to the right and then pulled briefly to the left. This movement creates a sudden compression of a P region of the coils. The compressed region travels along the spring (to the right in Fig- ure 16.3). The compressed region is followed by a region where the coils are extended. Notice that the direction of the displacement of the coils is parallel to the direction of propagation of the compressed region. P A traveling wave or pulse that causes the elements of the medium to move parallel to the direction of propagation is called a longitudinal wave. P Sound waves, which we shall discuss in Chapter 17, are another example of longitu- dinal waves. The disturbance in a sound wave is a series of high-pressure and low- pressure regions that travel through air. Figure 16.2 A transverse pulse Some waves in nature exhibit a combination of transverse and longitudinal dis- traveling on a stretched rope. The direction of motion of any element placements. Surface water waves are a good example. When a water wave travels on the P of the rope (blue arrows) is per- surface of deep water, elements of water at the surface move in nearly circular paths, as pendicular to the direction of shown in Figure 16.4. Note that the disturbance has both transverse and longitudinal propagation (red arrows). Compressed Compressed Stretched Stretched Figure 16.3 A longitudinal pulse along a stretched spring. The displacement of the coils is parallel to the direction of the propagation. 1 In reality, the pulse changes shape and gradually spreads out during the motion. This effect is called dispersion and is common to many mechanical waves as well as to electromagnetic waves. We do not consider dispersion in this chapter. SECTION 16.1 • Propagation of a Disturbance 489 Velocity of propagation Active Figure 16.4 The motion of water elements on the surface of deep water in which a wave is propagating is a combination of transverse and longitudinal displace- ments, with the result that elements at the surface move in nearly circular paths. Each element is displaced both horizontally and vertically from its equilibrium position. At the Active Figures link at http://www.pse6.com, you can observe the displacement of water elements at the surface of the moving waves. components. The transverse displacements seen in Figure 16.4 represent the variations in vertical position of the water elements. The longitudinal displacement can be ex- plained as follows: as the wave passes over the water’s surface, water elements at the highest points move in the direction of propagation of the wave, whereas elements at the lowest points move in the direction opposite the propagation. The three-dimensional waves that travel out from points under the Earth’s surface along a fault at which an earthquake occurs are of both types—transverse and longitu- dinal. The longitudinal waves are the faster of the two, traveling at speeds in the range of 7 to 8 km/s near the surface. These are called P waves (with “P” standing for pri- mary) because they travel faster than the transverse waves and arrive at a seismograph (a device used to detect waves due to earthquakes) first. The slower transverse waves, called S waves (with “S” standing for secondary), travel through the Earth at 4 to 5 km/s near the surface. By recording the time interval between the arrivals of these two types of waves at a seismograph, the distance from the seismograph to the point of ori- gin of the waves can be determined.
Load more

Recommended publications
  • Rotational and Translational Waves in a Bowed String Eric Bavu, Manfred Yew, Pierre-Yves Pla•Ais, John Smith and Joe Wolfe
    Proceedings of the International Symposium on Musical Acoustics, March 31st to April 3rd 2004 (ISMA2004), Nara, Japan Rotational and translational waves in a bowed string Eric Bavu, Manfred Yew, Pierre-Yves Pla•ais, John Smith and Joe Wolfe School of Physics, University of New South Wales, Sydney Australia [email protected] relative motion of the bow and string, and therefore the Abstract times of commencement of stick and slip phases, We measure and compare the rotational and transverse depends on both the transverse and torsional velocity velocity of a bowed string. When bowed by an (Fig 2). Consequently, torsional waves can introduce experienced player, the torsional motion is phase-locked aperiodicity or jitter to the motion of the string. Human to the transverse waves, producing highly periodic hearing is very sensitive to jitter [9]. Small amounts of motion. The spectrum of the torsional motion includes jitter contribute to a sound's being identified as 'natural' the fundamental and harmonics of the transverse wave, rather than 'mechanical'. Large amounts of jitter, on the with strong formants at the natural frequencies of the other hand, sound unmusical. Here we measure and torsional standing waves in the whole string. Volunteers compare translational and torsional velocities of a with no experience on bowed string instruments, bowed bass string and examine the periodicity of the however, often produced non-periodic motion. We standing waves. present sound files of both the transverse and torsional velocity signals of well-bowed strings. The torsional y string signal has not only the pitch of the transverse signal, but kink it sounds recognisably like a bowed string, probably because of its rich harmonic structure and the transients and amplitude envelope produced by bowing.
    [Show full text]
  • The Science of String Instruments
    The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D.
    [Show full text]
  • Acoustic Phonon Scattering from Particles Embedded in an Anisotropic Medium: a Molecular Dynamics Study
    University of Pennsylvania ScholarlyCommons Department of Mechanical Engineering & Departmental Papers (MEAM) Applied Mechanics March 2008 Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study Neil Zuckerman University of Pennsylvania Jennifer R. Lukes University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/meam_papers Recommended Citation Zuckerman, Neil and Lukes, Jennifer R., "Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study" (2008). Departmental Papers (MEAM). 145. https://repository.upenn.edu/meam_papers/145 Reprinted from Physical Review B, Volume 77, Article 094302, March 2008, 20 pages. Publisher URL: http://dx.doi.org/10.1103/PhysRevB.77.094302 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/meam_papers/145 For more information, please contact [email protected]. Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study Abstract Acoustic phonon scattering from isolated nanometer-scale impurity particles embedded in anisotropic media is investigated using molecular dynamics simulation. The spectral-directional dependence of the scattering, for both longitudinal and transverse modes, is found through calculation of scattering cross sections and three dimensional scattering phase functions for inclusions of varying sizes, shapes, and stiffnesses and for waves of different wave numbers. The
    [Show full text]
  • Standing Waves and Sound
    Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go.
    [Show full text]
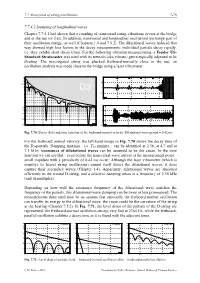
  • 7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
    7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples).
    [Show full text]
  • Giant Slinky: Quantitative Exhibit Activity
    Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position.
    [Show full text]
  • Curriculum Overview Physics/Pre-AP 2018-2019 1St Nine Weeks
    Curriculum Overview Physics/Pre-AP 2018-2019 1st Nine Weeks RESOURCES: Essential Physics (Ergopedia – online book) Physics Classroom http://www.physicsclassroom.com/ PHET Simulations https://phet.colorado.edu/ ONGOING TEKS: 1A, 1B, 2A, 2B, 2C, 2D, 2F, 2G, 2H, 2I, 2J,3E 1) SAFETY TEKS 1A, 1B Vocabulary Fume hood, fire blanket, fire extinguisher, goggle sanitizer, eye wash, safety shower, impact goggles, chemical safety goggles, fire exit, electrical safety cut off, apron, broken glass container, disposal alert, biological hazard, open flame alert, thermal safety, sharp object safety, fume safety, electrical safety, plant safety, animal safety, radioactive safety, clothing protection safety, fire safety, explosion safety, eye safety, poison safety, chemical safety Key Concepts The student will be able to determine if a situation in the physics lab is a safe practice and what appropriate safety equipment and safety warning signs may be needed in a physics lab. The student will be able to determine the proper disposal or recycling of materials in the physics lab. Essential Questions 1. How are safe practices in school, home or job applied? 2. What are the consequences for not using safety equipment or following safe practices? 2) SCIENCE OF PHYSICS: Glossary, Pages 35, 39 TEKS 2B, 2C Vocabulary Matter, energy, hypothesis, theory, objectivity, reproducibility, experiment, qualitative, quantitative, engineering, technology, science, pseudo-science, non-science Key Concepts The student will know that scientific hypotheses are tentative and testable statements that must be capable of being supported or not supported by observational evidence. The student will know that scientific theories are based on natural and physical phenomena and are capable of being tested by multiple independent researchers.
    [Show full text]
  • Woods for Wooden Musical Instruments S
    ISMA 2014, Le Mans, France Woods for Wooden Musical Instruments S. Yoshikawaa and C. Walthamb aKyushu University, Graduate School of Design, 4-9-1 Shiobaru, Minami-ku, 815-8540 Fukuoka, Japan bUniversity of British Columbia, Dept of Physics & Astronomy, 6224 Agricultural Road, Vancouver, BC, Canada V6T 1Z1 [email protected] 281 ISMA 2014, Le Mans, France In spite of recent advances in materials science, wood remains the preferred construction material for musical instruments worldwide. Some distinguishing features of woods (light weight, intermediate quality factor, etc.) are easily noticed if we compare material properties between woods, a plastic (acrylic), and a metal (aluminum). Woods common in musical instruments (strings, woodwinds, and percussions) are typically (with notable exceptions) softwoods (e.g. Sitka spruce) as tone woods for soundboards, hardwoods (e.g. amboyna) as frame woods for backboards, and monocots (e.g. bamboo) as bore woods for woodwind bodies. Moreover, if we consider the radiation characteristics of tap tones from sample plates of Sitka spruce, maple, and aluminum, a large difference is observed above around 2 kHz that is attributed to the relative strength of shear and bending deformations in flexural vibrations. This shear effect causes an appreciable increase in the loss factor at higher frequencies. The stronger shear effect in Sitka spruce than in maple and aluminum seems to be relevant to soundboards because its low-pass filter effect with a cutoff frequency of about 2 kHz tends to lend the radiated sound a desired softness. A classification diagram of traditional woods based on an anti-vibration parameter (density ρ/sound speed c) and transmission parameter cQ is proposed.
    [Show full text]
  • University of California Santa Cruz the Vietnamese Đàn
    UNIVERSITY OF CALIFORNIA SANTA CRUZ THE VIETNAMESE ĐÀN BẦU: A CULTURAL HISTORY OF AN INSTRUMENT IN DIASPORA A dissertation submitted in partial satisfaction of the requirements for the degree of DOCTOR OF PHILOSOPHY in MUSIC by LISA BEEBE June 2017 The dissertation of Lisa Beebe is approved: _________________________________________________ Professor Tanya Merchant, Chair _________________________________________________ Professor Dard Neuman _________________________________________________ Jason Gibbs, PhD _____________________________________________________ Tyrus Miller Vice Provost and Dean of Graduate Studies Table of Contents List of Figures .............................................................................................................................................. v Chapter One. Introduction ..................................................................................................................... 1 Geography: Vietnam ............................................................................................................................. 6 Historical and Political Context .................................................................................................... 10 Literature Review .............................................................................................................................. 17 Vietnamese Scholarship .............................................................................................................. 17 English Language Literature on Vietnamese Music
    [Show full text]
  • Chapter 5 Waves I: Generalities, Superposition & Standing Waves
    Chapter 5 Waves I: Generalities, Superposition & Standing Waves 5.1 The Important Stuff 5.1.1 Wave Motion Wave motion occurs when the mass elements of a medium such as a taut string or the surface of a liquid make relatively small oscillatory motions but collectively give a pattern which travels for long distances. This kind of motion also includes the phenomenon of sound, where the molecules in the air around us make small oscillations but collectively give a disturbance which can travel the length of a college classroom, all the way to the students dozing in the back. We can even view the up–and–down motion of inebriated spectators of sports events as wave motion, since their small individual motions give rise to a disturbance which travels around a stadium. The mathematics of wave motion also has application to electromagnetic waves (including visible light), though the physical origin of those traveling disturbances is quite different from the mechanical waves we study in this chapter; so we will hold off on studying electromagnetic waves until we study electricity and magnetism in the second semester of our physics course. Obviously, wave motion is of great importance in physics and engineering. 5.1.2 Types of Waves In some types of wave motion the motion of the elements of the medium is (for the most part) perpendicular to the motion of the traveling disturbance. This is true for waves on a string and for the people–wave which travels around a stadium. Such a wave is called a transverse wave. This type of wave is the easiest to visualize.
    [Show full text]
  • 1S-13 Slinky on Stand
    Sound light waves... waves... water waves... 1S-13 Slinky on Stand Creating longitudinal compression waves in a slinky What happens when you pull back and release one end of the slinky ? Physics 214 Fall 2010 11/18/2019 3 Moving one end of the Slinky back and forth created a local compression where the rings of the spring are closer together than in the rest of the Slinky. The slinky tries to return to equilibrium. But inertia cause the links to pass beyond. This create a compression. Then the links comes back to the equilibrium point due to the restoration force, i.e. the elastic force. The speed of the pulse may depend on factors such as tension in the Slinky and the mass of the Slinky. Energy is transferred through the Slinky as the pulse travels. The work done in moving one end of the Slinky increases both the potential energy of the spring and the kinetic energy of individual loops. This region of higher energy then moves along the Slinky and reaches the opposite end. There, the energy could be used to ring a bell or perform other types of work. Energy carried by water waves does substantial work over time in eroding and shaping a shoreline. If instead of moving your hand back and forth just once, you continue to produce pulses, you will send a series of longitudinal pulses down the Slinky. If equal time intervals separate the pulses, you produce a periodic wave. The time between pulses is the period T of the wave. The number of pulses or cycles per unit of time is the frequency f = 1/T.
    [Show full text]
  • Class Summer Vacation, 2021-22 Subject
    HOLIDAY HOMEWORK: Class 10 IG Summer Vacation, 2021-22 Subject : English Literature Time to be Spent One hour for fifteen days (Hours per day for ___ Days) : Work Read the text of Shakespeare’s Othello. Specification : Materials Hard copy or soft copy of the text of the drama Othello Required : Read the original text and the paraphrase. Make a presentation in about 15 slides . Some online resources are shared below: https://www.youtube.com/watch?v=2aRr6-XXAD8 Instructions / https://www.youtube.com/watch?v=95Vfcb7VvCA Guidelines : https://www.youtube.com/watch?v=Bp6LqSgukOU https://www.youtube.com/watch?v=lN4Kpj1PFKM https://www.youtube.com/watch?v=5z19M1A8MtY Any other Information: 1. List of the characters. 2. Theme of the drama 3. Act wise summary Date of Submission: 30th June 2021 ( you have to present your research in classroom) Head of the Department HOLIDAY HOMEWORK: Class 10 IG Summer Vacation, 2021-22 Subject : BUSINESS STUDIES (0450) Time to be Spent 6 Hours (1 ½ Hours per day for 4 Days) : Past papers for both components. Work Specification : Materials BUSINESS STUDIES (0450) TEXT BOOK Required : Students are expected to take printout of papers using the link: https://drive.google.com/file/d/1RJO1dBuq2eceLwKZ3ptolKL5JZP76rKW/view?usp=sharing Student should strictly avoid copying the answers from the books/ marking Instructions / scheme for their own benefit and well- being. Guidelines: Students are expected to take a print of all the papers given, get them spiral-bind and solve them in the space provided in the question paper itself and avoid taking extra sheet. Any other Information: Answers must fulfill all the criteria of assessment objectives.
    [Show full text]