DOCSLIB.ORG

6Th Grade Math At-Home Learning Packet

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
6Th Grade Math At-Home Learning Packet At-HomeLearning Instructions for 5.11-5.22 6th grade Math At-Home Learning Packet Notes & Assignments for 5.11-5.22 Lesson: 10.4 Interquartile Range and Box Plots ○ p. 561-566 ○ Work through the lesson: complete Learn- Examples- Check- Apply Assignment: Practice 10.4 F riday 5.15 ● P.567-568 ● You will need to submit this assignment to your teacher Lesson 10.6 Outliers ○ p. 575-580 ○ Work through the lesson: complete Learn- Examples- Check- Apply Assignment: Practice 10.6 Due Friday 5.22 ● P.581-582 ● You will need to submit this assignment to your teacher Lesson 10-4 Interquartile Range and Box Plots I Can... understand how a measure of variation describes the What Vocabulary variability of a data set with a single value, display a numerical data Will You Learn? set in a box plot, and summarize the data. box plot first quartile interquartile range Learn Measures of Variation measures of variation Measures of variation are values that describe the variability, or quartiles spread, of a data set. They describe how the values of a data set range vary with a single number. second quartile third quartile One measure of variation is the range, which is the difference between the greatest and least data values in a data set. Consider the data set shown. The data values range from 0 to 8. 0, 0, 1, 1, 2, 2, 2, 3, 4, 5, 6, 6, 7, 7, 7, 8 The range is 8–0, or 8. Another measure of variation is the interquartile range. Before you can find this measure, you first need to understand and find quartiles. Quartiles divide the data into four equal parts. The first quartile, Q1, is the median of the data values less than the median. The third quartile, Q3, is the median of the data values greater than the Talk About It! median. The median is also known as the second quartile, Q2. How does knowing Median (Q2) = 3.5 that the data is divided The median divides the data into four equal parts Q1 = 1.5 Q3 = 6.5 into two halves. The quartiles help you remember divide the data into fourths. the vocabulary term 25% 25% 25% 25% Each fourth represents 25% quartile? of the data. 0, 0, 1, 1, 2, 2, 2, 3, 4, 5, 6, 6, 7, 7, 7, 8 See students’ responses. Lower Half Upper Half Talk About It! The interquartile range (IQR) is the distance between the first and third quartiles of the data set. To find the IQR, subtract the first If the median describes the center Copyright © McGraw-Hill Education Copyright © McGraw-Hill quartile from the third quartile. IQR = 6.5 - 1.5, or 5 of a data set, what The interquartile range does the interquartile represents the middle half, or Q1 = 1.5 Q3 = 6.5 range describe? middle 50%, of the data. The Sample answer: The lower the IQR is for a data set, 25% 25% 25% 25% the closer the middle half of the interquartile range 0, 0, 1, 1, 2, 2, 2, 3, 4, 5, 6, 6, 7, 7, 7, 8 data is to the median. describes how spread 50% out the middle 50% of the values are around In the given data set, the IQR is 6.5 - 1.5, or 5. the median. Lesson 10-4 • Interquartile Range and Box Plots 561 THIS MATERIAL IS PROVIDED FOR INDIVIDUAL EDUCATIONAL PURPOSES ONLY AND MAY NOT BE DOWNLOADED, REPRODUCED, OR FURTHER DISTRIBUTED. Your Notes Example 1 Find the Range and Interquartile Range The table shows the approximate Animal Speed (mph) maximum speeds, in miles per hour, of different animals. Housecat 30 Think About It! Cheetah 70 Use the range and interquartile range Do the data values to describe how the data vary. Elephant 25 need to be in numerical order? Why? Lion 50 Part A Describe the variation of the Mouse 8 yes; You need to find data using the range. Spider 1 the middle number. The greatest speed in the data set is 70 miles per hour. The least speed in the data set is 1 mile per hour. The range is 70 - 1, or 69 miles per hour. The speeds of animals vary by 69 miles per hour. Talk About It! Which value, the interquartile range, the Part B Describe the variation of the data using the interquartile first quartile, or the range. third quartile tells you more about the spread Step 1 Find the median. of the data values? Write the speeds in order from least to greatest. Explain your reasoning. Sample answer: The 1 8 25 30 50 70 interquartile range tells you more about least greatest Find the mean of the two middle numbers, the spread of the The median is 27.5 . data, specifically the 25 and 30. spread of the middle Education Copyright © McGraw-Hill Step 2 Find the first and third quartiles. half of the data. The first quartile is 8 . Find the median of the lower half of the data. The third quartile is 50 . Find the median of the upper half of the data. Step 3 Find the interquartile range. Interquartile range = Q 3 - Q 1 = 50 - 8 Q 3 = 50; Q 1 = 8 = 42 Subtract. So, the spread of the middle 50% of the data is 42 . This means that the middle half of the data values vary by 42 miles per hour. 562 Module 10 • Statistical Measures and Displays THIS MATERIAL IS PROVIDED FOR INDIVIDUAL EDUCATIONAL PURPOSES ONLY AND MAY NOT BE DOWNLOADED, REPRODUCED, OR FURTHER DISTRIBUTED. 561-568_MSM_SE_C1M10_L4_899714.indd 09/11/18 03:39PM 561-568_MSM_SE_C1M10_L4_899714.indd Program: MSM Component: Lesson PDF Pass Vendor: LDL Grade: 6-8 Check The average wind speeds for several Wind Speed cities in Pennsylvania are given in the City Speed (mph) table. Use the range and interquartile range to describe how the data vary. Allentown 8.9 Erie 11.0 Part A Harrisburg 7.5 Describe the variation of the data Middletown 7.7 using the range. Philadelphia 9.5 Show The data vary by a range of your work Pittsburgh 9.0 here 3.5 miles per hour. Williamsport 7.6 Part B Math History Minute Describe the variation of the data using the interquartile range. Florence Nightingale Show The middle half of the data values vary by 1.9 (1820–1910) used your work here miles per hour. statistics to help improve the survival rates of hospital patients. She Go Online You can complete an Extra Example online. discovered that by improving sanitation, survival rates improved. Learn Construct Box Plots She designed charts to A box plot, or box-and-whisker plot, uses a number line to show the display the data, as distribution of a data set by plotting the median, quartiles, and statistics had rarely been presented with extreme values. The extreme values, or extremes, are the greatest charts before. She is and least values in the data set. The extremes, quartiles, and median known for inventing the are referred to as the five-number summary. coxcomb graph, which A box is drawn around the two quartile values. The whiskers extend is a variation of the from each quartile to the extreme data values, unless the extremes circle graph. are very far apart from the rest of the data set. The median is marked with a vertical line, and separates the box into two boxes. lower upper extreme Q1 median Q2 extreme Copyright © McGraw-Hill Education Copyright © McGraw-Hill Box plots separate data into four sections. These sections are visual representations of quartiles. Even though the parts may differ in length, each contain 25% of the data. The two boxes represent the middle 50% of the data. A longer box or whisker indicates the data are more spread out in that section. A longer box or whisker does not mean there are more data values in that section. Each section contains the same number of values, 25% of the data. Lesson 10-4 • Interquartile Range and Box Plots 563 THIS MATERIAL IS PROVIDED FOR INDIVIDUAL EDUCATIONAL PURPOSES ONLY AND MAY NOT BE DOWNLOADED, REPRODUCED, OR FURTHER DISTRIBUTED. 30/11/18 05:14PM 561-568_MSM_SE_C1M10_L4_899714.indd 30/11/18 05:14PM Program: MSM Component: Lesson PDF Pass Vendor: LDL Grade: 6-8 Example 2 Think About It! Interpret Box Plots What does the length The box plot shows the annual snowfall totals, in inches, for a certain of the box and city over a period of 20 years. whiskers tell you about the spread of the data Annual Snowfall (in.) in the box plot? See students’ responses. 100 120 140 160 180 200 220 240 260 Describe the distribution of the data. What does it tell you about the snowfall in this city? The annual snowfall ranges from about 110 inches to about 250 Talk About It! inches. The middle half of the data range from about 140 inches to What does the about 195 inches. Because the boxes are shorter than the whiskers, interquartile range there is less variation among the middle half of the data. Having less describe in the context variation means there is a greater consistency among the middle of the problem? 50% of the data than in either whisker. Sample answer: The middle 50% of the data Check is clustered between The average gas mileage, in miles per gallon, for various sedans is about 140 inches and shown in the box plot. Describe the distribution of the data. What 195 inches. So, in half does it tell you about the average gas mileage for those sedans? of the years, the city received between 140 Average Gas Mileage (mpg) inches and 195 inches of snow.
Load more

Recommended publications
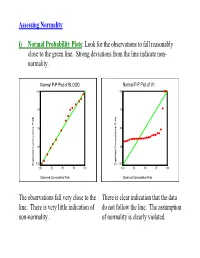
  • Assessing Normality I) Normal Probability Plots : Look for The
    Assessing Normality i) Normal Probability Plots: Look for the observations to fall reasonably close to the green line. Strong deviations from the line indicate non- normality. Normal P-P Plot of BLOOD Normal P-P Plot of V1 1.00 1.00 .75 .75 .50 .50 .25 .25 0.00 0.00 Expected Cummulative Prob Expected Cummulative Expected Cummulative Prob Expected Cummulative 0.00 .25 .50 .75 1.00 0.00 .25 .50 .75 1.00 Observed Cummulative Prob Observed Cummulative Prob The observations fall very close to the There is clear indication that the data line. There is very little indication of do not follow the line. The assumption non-normality. of normality is clearly violated. ii) Histogram: Look for a “bell-shape”. Severe skewness and/or outliers are indications of non-normality. 5 16 14 4 12 10 3 8 2 6 4 1 Std. Dev = 60.29 Std. Dev = 992.11 2 Mean = 274.3 Mean = 573.1 0 N = 20.00 0 N = 25.00 150.0 200.0 250.0 300.0 350.0 0.0 1000.0 2000.0 3000.0 4000.0 175.0 225.0 275.0 325.0 375.0 500.0 1500.0 2500.0 3500.0 4500.0 BLOOD V1 Although the histogram is not perfectly There is a clear indication that the data symmetric and bell-shaped, there is no are right-skewed with some strong clear violation of normality. outliers. The assumption of normality is clearly violated. Caution: Histograms are not useful for small sample sizes as it is difficult to get a clear picture of the distribution.
    [Show full text]
  • Lesson 7: Measuring Variability for Skewed Distributions (Interquartile Range)
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 7 M2 ALGEBRA I Lesson 7: Measuring Variability for Skewed Distributions (Interquartile Range) Student Outcomes . Students explain why a median is a better description of a typical value for a skewed distribution. Students calculate the 5-number summary of a data set. Students construct a box plot based on the 5-number summary and calculate the interquartile range (IQR). Students interpret the IQR as a description of variability in the data. Students identify outliers in a data distribution. Lesson Notes Distributions that are not symmetrical pose some challenges in students’ thinking about center and variability. The observation that the distribution is not symmetrical is straightforward. The difficult part is to select a measure of center and a measure of variability around that center. In Lesson 3, students learned that, because the mean can be affected by unusual values in the data set, the median is a better description of a typical data value for a skewed distribution. This lesson addresses what measure of variability is appropriate for a skewed data distribution. Students construct a box plot of the data using the 5-number summary and describe variability using the interquartile range. Classwork Exploratory Challenge 1/Exercises 1–3 (10 minutes): Skewed Data and Their Measure of Center Verbally introduce the data set as described in the introductory paragraph and dot plot shown below. Exploratory Challenge 1/Exercises 1–3: Skewed Data and Their Measure of Center Consider the following scenario. A television game show, Fact or Fiction, was cancelled after nine shows. Many people watched the nine shows and were rather upset when it was taken off the air.
    [Show full text]
  • Fan Chart: Methodology and Its Application to Inflation Forecasting in India
    W P S (DEPR) : 5 / 2011 RBI WORKING PAPER SERIES Fan Chart: Methodology and its Application to Inflation Forecasting in India Nivedita Banerjee and Abhiman Das DEPARTMENT OF ECONOMIC AND POLICY RESEARCH MAY 2011 The Reserve Bank of India (RBI) introduced the RBI Working Papers series in May 2011. These papers present research in progress of the staff members of RBI and are disseminated to elicit comments and further debate. The views expressed in these papers are those of authors and not that of RBI. Comments and observations may please be forwarded to authors. Citation and use of such papers should take into account its provisional character. Copyright: Reserve Bank of India 2011 Fan Chart: Methodology and its Application to Inflation Forecasting in India Nivedita Banerjee 1 (Email) and Abhiman Das (Email) Abstract Ever since Bank of England first published its inflation forecasts in February 1996, the Fan Chart has been an integral part of inflation reports of central banks around the world. The Fan Chart is basically used to improve presentation: to focus attention on the whole of the forecast distribution, rather than on small changes to the central projection. However, forecast distribution is a technical concept originated from the statistical sampling distribution. In this paper, we have presented the technical details underlying the derivation of Fan Chart used in representing the uncertainty in inflation forecasts. The uncertainty occurs because of the inter-play of the macro-economic variables affecting inflation. The uncertainty in the macro-economic variables is based on their historical standard deviation of the forecast errors, but we also allow these to be subjectively adjusted.
    [Show full text]
  • Finding Basic Statistics Using Minitab 1. Put Your Data Values in One of the Columns of the Minitab Worksheet
    Finding Basic Statistics Using Minitab 1. Put your data values in one of the columns of the Minitab worksheet. 2. Add a variable name in the gray box just above the data values. 3. Click on “Stat”, then click on “Basic Statistics”, and then click on "Display Descriptive Statistics". 4. Choose the variable you want the basic statistics for click on “Select”. 5. Click on the “Statistics” box and then check the box next to each statistic you want to see, and uncheck the boxes next to those you do not what to see. 6. Click on “OK” in that window and click on “OK” in the next window. 7. The values of all the statistics you selected will appear in the Session window. Example (Navidi & Monk, Elementary Statistics, 2nd edition, #31 p. 143, 1st 4 columns): This data gives the number of tribal casinos in a sample of 16 states. 3 7 14 114 2 3 7 8 26 4 3 14 70 3 21 1 Open Minitab and enter the data under C1. The table below shows a portion of the entered data. ↓ C1 C2 Casinos 1 3 2 7 3 14 4 114 5 2 6 3 7 7 8 8 9 26 10 4 Now click on “Stat” and then choose “Basic Statistics” and “Display Descriptive Statistics”. Click in the box under “Variables:”, choose C1 from the window at left, and then click on the “Select” button. Next click on the “Statistics” button and choose which statistics you want to find. We will usually be interested in the following statistics: mean, standard error of the mean, standard deviation, minimum, maximum, range, first quartile, median, third quartile, interquartile range, mode, and skewness.
    [Show full text]
  • Continuous Random Variables
    ST 380 Probability and Statistics for the Physical Sciences Continuous Random Variables Recall: A continuous random variable X satisfies: 1 its range is the union of one or more real number intervals; 2 P(X = c) = 0 for every c in the range of X . Examples: The depth of a lake at a randomly chosen location. The pH of a random sample of effluent. The precipitation on a randomly chosen day is not a continuous random variable: its range is [0; 1), and P(X = c) = 0 for any c > 0, but P(X = 0) > 0. 1 / 12 Continuous Random Variables Probability Density Function ST 380 Probability and Statistics for the Physical Sciences Discretized Data Suppose that we measure the depth of the lake, but round the depth off to some unit. The rounded value Y is a discrete random variable; we can display its probability mass function as a bar graph, because each mass actually represents an interval of values of X . In R source("discretize.R") discretize(0.5) 2 / 12 Continuous Random Variables Probability Density Function ST 380 Probability and Statistics for the Physical Sciences As the rounding unit becomes smaller, the bar graph more accurately represents the continuous distribution: discretize(0.25) discretize(0.1) When the rounding unit is very small, the bar graph approximates a smooth function: discretize(0.01) plot(f, from = 1, to = 5) 3 / 12 Continuous Random Variables Probability Density Function ST 380 Probability and Statistics for the Physical Sciences The probability that X is between two values a and b, P(a ≤ X ≤ b), can be approximated by P(a ≤ Y ≤ b).
    [Show full text]
  • Normal Probability Distribution
    MATH2114 Week 8, Thursday The Normal Distribution Slides Adopted & modified from “Business Statistics: A First Course” 7th Ed, by Levine, Szabat and Stephan, 2016 Pearson Education Inc. Objective/Goals To compute probabilities from the normal distribution How to use the normal distribution to solve practical problems To use the normal probability plot to determine whether a set of data is approximately normally distributed Continuous Probability Distributions A continuous variable is a variable that can assume any value on a continuum (can assume an uncountable number of values) thickness of an item time required to complete a task temperature of a solution height, in inches These can potentially take on any value depending only on the ability to precisely and accurately measure The Normal Distribution Bell Shaped f(X) Symmetrical Mean=Median=Mode σ Location is determined by X the mean, μ μ Spread is determined by the standard deviation, σ Mean The random variable has an = Median infinite theoretical range: = Mode + to The Normal Distribution Density Function The formula for the normal probability density function is 2 1 (X μ) 1 f(X) e 2 2π Where e = the mathematical constant approximated by 2.71828 π = the mathematical constant approximated by 3.14159 μ = the population mean σ = the population standard deviation X = any value of the continuous variable The Normal Distribution Density Function By varying 휇 and 휎, we obtain different normal distributions Image taken from Wikipedia, released under public domain The
    [Show full text]
  • 2018 Statistics Final Exam Academic Success Programme Columbia University Instructor: Mark England
    2018 Statistics Final Exam Academic Success Programme Columbia University Instructor: Mark England Name: UNI: You have two hours to finish this exam. § Calculators are necessary for this exam. § Always show your working and thought process throughout so that even if you don’t get the answer totally correct I can give you as many marks as possible. § It has been a pleasure teaching you all. Try your best and good luck! Page 1 Question 1 True or False for the following statements? Warning, in this question (and only this question) you will get minus points for wrong answers, so it is not worth guessing randomly. For this question you do not need to explain your answer. a) Correlation values can only be between 0 and 1. False. Correlation values are between -1 and 1. b) The Student’s t distribution gives a lower percentage of extreme events occurring compared to a normal distribution. False. The student’s t distribution gives a higher percentage of extreme events. c) The units of the standard deviation of � are the same as the units of �. True. d) For a normal distribution, roughly 95% of the data is contained within one standard deviation of the mean. False. It is within two standard deviations of the mean e) For a left skewed distribution, the mean is larger than the median. False. This is a right skewed distribution. f) If an event � is independent of �, then � (�) = �(�|�) is always true. True. g) For a given confidence level, increasing the sample size of a survey should increase the margin of error.
    [Show full text]
  • Binomial and Normal Distributions
    Probability distributions Introduction What is a probability? If I perform n experiments and a particular event occurs on r occasions, the “relative frequency” of r this event is simply . This is an experimental observation that gives us an estimate of the n probability – there will be some random variation above and below the actual probability. If I do a large number of experiments, the relative frequency gets closer to the probability. We define the probability as meaning the limit of the relative frequency as the number of experiments tends to infinity. Usually we can calculate the probability from theoretical considerations (number of beads in a bag, number of faces of a dice, tree diagram, any other kind of statistical model). What is a random variable? A random variable (r.v.) is the value that might be obtained from some kind of experiment or measurement process in which there is some random uncertainty. A discrete r.v. takes a finite number of possible values with distinct steps between them. A continuous r.v. takes an infinite number of values which vary smoothly. We talk not of the probability of getting a particular value but of the probability that a value lies between certain limits. Random variables are given names which start with a capital letter. An r.v. is a numerical value (eg. a head is not a value but the number of heads in 10 throws is an r.v.) Eg the score when throwing a dice (discrete); the air temperature at a random time and date (continuous); the age of a cat chosen at random.
    [Show full text]
  • L-Moments Based Assessment of a Mixture Model for Frequency Analysis of Rainfall Extremes
    Advances in Geosciences, 2, 331–334, 2006 SRef-ID: 1680-7359/adgeo/2006-2-331 Advances in European Geosciences Union Geosciences © 2006 Author(s). This work is licensed under a Creative Commons License. L-moments based assessment of a mixture model for frequency analysis of rainfall extremes V. Tartaglia, E. Caporali, E. Cavigli, and A. Moro Dipartimento di Ingegneria Civile, Universita` degli Studi di Firenze, Italy Received: 2 December 2004 – Revised: 2 October 2005 – Accepted: 3 October 2005 – Published: 23 January 2006 Abstract. In the framework of the regional analysis of hy- events in Tuscany (central Italy), a statistical methodology drological extreme events, a probabilistic mixture model, for parameter estimation of a probabilistic mixture model is given by a convex combination of two Gumbel distributions, here developed. The use of a probabilistic mixture model in is proposed for rainfall extremes modelling. The papers con- the regional analysis of rainfall extreme events, comes from cerns with statistical methodology for parameter estimation. the hypothesis that rainfall phenomenon arises from two in- With this aim, theoretical expressions of the L-moments of dependent populations (Becchi et al., 2000; Caporali et al., the mixture model are here defined. The expressions have 2002). The first population describes the basic components been tested on the time series of the annual maximum height corresponding to the more frequent events of low magnitude, of daily rainfall recorded in Tuscany (central Italy). controlled by the local morpho-climatic conditions. The sec- ond population characterizes the outlier component of more intense and rare events, which is here considered due to the aggregation at the large scale of meteorological phenomena.
    [Show full text]
  • Estimation of Quantiles and the Interquartile Range in Complex Surveys Carol Ann Francisco Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1987 Estimation of quantiles and the interquartile range in complex surveys Carol Ann Francisco Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Statistics and Probability Commons Recommended Citation Francisco, Carol Ann, "Estimation of quantiles and the interquartile range in complex surveys " (1987). Retrospective Theses and Dissertations. 11680. https://lib.dr.iastate.edu/rtd/11680 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS While the most advanced technology has been used to photograph and reproduce this manuscript, the quality of the reproduction is heavily dependent upon the quality of the material submitted. For example: • Manuscript pages may have indistinct print. In such cases, the best available copy has been filmed. • Manuscripts may not always be complete. In such cases, a note will indicate that it is not possible to obtain missing pages. • Copyrighted material may have been removed from the manuscript. In such cases, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, and charts) are photographed by sectioning the original, beginning at the upper left-hand corner and continuing from left to right in equal sections with small overlaps. Each oversize page is also filmed as one exposure and is available, for an additional charge, as a standard 35mm slide or as a 17"x 23" black and white photographic print.
    [Show full text]
  • On Median and Quartile Sets of Ordered Random Variables*
    ISSN 2590-9770 The Art of Discrete and Applied Mathematics 3 (2020) #P2.08 https://doi.org/10.26493/2590-9770.1326.9fd (Also available at http://adam-journal.eu) On median and quartile sets of ordered random variables* Iztok Banicˇ Faculty of Natural Sciences and Mathematics, University of Maribor, Koroskaˇ 160, SI-2000 Maribor, Slovenia, and Institute of Mathematics, Physics and Mechanics, Jadranska 19, SI-1000 Ljubljana, Slovenia, and Andrej Marusiˇ cˇ Institute, University of Primorska, Muzejski trg 2, SI-6000 Koper, Slovenia Janez Zerovnikˇ Faculty of Mechanical Engineering, University of Ljubljana, Askerˇ cevaˇ 6, SI-1000 Ljubljana, Slovenia, and Institute of Mathematics, Physics and Mechanics, Jadranska 19, SI-1000 Ljubljana, Slovenia Received 30 November 2018, accepted 13 August 2019, published online 21 August 2020 Abstract We give new results about the set of all medians, the set of all first quartiles and the set of all third quartiles of a finite dataset. We also give new and interesting results about rela- tionships between these sets. We also use these results to provide an elementary correctness proof of the Langford’s doubling method. Keywords: Statistics, probability, median, first quartile, third quartile, median set, first quartile set, third quartile set. Math. Subj. Class. (2020): 62-07, 60E05, 60-08, 60A05, 62A01 1 Introduction Quantiles play a fundamental role in statistics: they are the critical values used in hypoth- esis testing and interval estimation. Often they are the characteristics of distributions we usually wish to estimate. The use of quantiles as primary measure of performance has *This work was supported in part by the Slovenian Research Agency (grants J1-8155, N1-0071, P2-0248, and J1-1693.) E-mail addresses: [email protected] (Iztok Banic),ˇ [email protected] (Janez Zerovnik)ˇ cb This work is licensed under https://creativecommons.org/licenses/by/4.0/ 2 Art Discrete Appl.
    [Show full text]
  • Boxplots for Grouped and Clustered Data in Toxicology
    Penultimate version. If citing, please refer instead to the published version in Archives of Toxicology, DOI: 10.1007/s00204-015-1608-4. Boxplots for grouped and clustered data in toxicology Philip Pallmann1, Ludwig A. Hothorn2 1 Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, UK, Tel.: +44 (0)1524 592318, [email protected] 2 Institute of Biostatistics, Leibniz University Hannover, 30419 Hannover, Germany Abstract The vast majority of toxicological papers summarize experimental data as bar charts of means with error bars. While these graphics are easy to generate, they often obscure essen- tial features of the data, such as outliers or subgroups of individuals reacting differently to a treatment. Especially raw values are of prime importance in toxicology, therefore we argue they should not be hidden in messy supplementary tables but rather unveiled in neat graphics in the results section. We propose jittered boxplots as a very compact yet comprehensive and intuitively accessible way of visualizing grouped and clustered data from toxicological studies together with individual raw values and indications of statistical significance. A web application to create these plots is available online. Graphics, statistics, R software, body weight, micronucleus assay 1 Introduction Preparing a graphical summary is usually the first if not the most important step in a data analysis procedure, and it can be challenging especially with many-faceted datasets as they occur frequently in toxicological studies. However, even in simple experimental setups many researchers have a hard time presenting their results in a suitable manner. Browsing recent volumes of this journal, we have realized that the least favorable ways of displaying toxicological data appear to be the most popular ones (according to the number of publications that use them).
    [Show full text]