DOCSLIB.ORG

Advanced Mathematics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Advanced Mathematics MSc FM, MTF, QF Induction Programme Advanced Mathematics Academic year 2010/2011 Lecture notes prepared by Laura Ballotta and George Harrison Section I Linear Algebra Differential Calculus Integral Calculus Difference and Differential Equations Table Content 1 LINEAR ALGEBRA .................................................................................................................................... 5 1.1. WHAT IS A MATRIX?................................................................................................................................. 5 1.2. SPECIAL TYPES OF MATRICES .................................................................................................................... 6 1.2.1. Vectors............................................................................................................................................ 6 1.2.2. Square matrix.................................................................................................................................. 6 1.2.3. Diagonal matrix .............................................................................................................................. 7 1.2.4. Identity Matrix................................................................................................................................ 7 1.3. MATRIX OPERATIONS ............................................................................................................................... 7 1.3.1 Adding and subtracting matrices .................................................................................................... 7 1.3.2 Scalar multiplication....................................................................................................................... 8 1.3.3. Transpose of a Matrix..................................................................................................................... 8 1.3.4. Vector multiplication ...................................................................................................................... 9 1.3.5 Matrix multiplication .................................................................................................................... 10 1.3.6 Properties of matrix multiplication ............................................................................................... 12 1.4. THE DETERMINANT................................................................................................................................. 13 1.4.1. How to find the determinant of a (2 x 2) matrix ........................................................................... 13 1.4.2. The determinant of a (3 x 3) matrix .............................................................................................. 14 1.4.3. Method of cofactors in determining determinants ........................................................................ 14 1.4.4. Properties of Determinants ........................................................................................................... 17 1.5. INVERSE OF A MATRIX............................................................................................................................. 18 1.5.1. Definition of an inverse matrix..................................................................................................... 18 1.5.2. How to find the inverse of a square matrix................................................................................... 18 1.6. TRACE OF A MATRIX............................................................................................................................... 19 1.7. SYSTEM OF LINEAR EQUATIONS ............................................................................................................. 20 1.8. PARTITIONED MATRICES......................................................................................................................... 22 1.9. VECTOR SPACES ...................................................................................................................................... 22 1.9.1 Rank of a matrix ........................................................................................................................... 25 1.10 EIGENVALUES AND EIGENVECTORS ................................................................................................... 26 1.10.1 General results for characteristic roots and vectors ...................................................................... 28 1.10.2 Further results on determining the rank of a matrix.................................................................... 29 1.11 DEFINITE MATRICES .......................................................................................................................... 29 2. DIFFERENTIAL CALCULUS .................................................................................................................. 32 2.1. DIFFERENTIATION ................................................................................................................................... 32 2.1.1. Definitions .................................................................................................................................... 32 2.1.2. Rules of Differentiation ................................................................................................................ 35 2.1.3. Derivatives of Exponential and logarithmic functions.................................................................. 37 2.1.4. Higher order derivatives............................................................................................................... 38 2.2. APPLICATIONS OF DERIVATIVES ............................................................................................................. 39 2.2.1. Taylor and Maclaurin Series......................................................................................................... 39 2.2.2. Increasing and decreasing functions ............................................................................................. 41 2.2.3. Concavity and Convexity.............................................................................................................. 42 2.2.4. First derivative test for relative extremum.................................................................................... 44 2.2.5. Second derivative test for relative extremum................................................................................ 45 2.2.6. The Nth-derivative test................................................................................................................. 46 2.2.7. Economic applications of derivatives ........................................................................................... 46 3. DIFFERENTIAL CALCULUS (THE MULTIVARIATE CASE) ............................................................. 53 3.1. MULTIVARIATE FUNCTIONS .................................................................................................................... 53 3.2 LIMITS AND CONTINUITY......................................................................................................................... 53 3.3 DIFFERENTIATION ................................................................................................................................... 55 3.4 APPLICATION OF DIFFERENTIATION ........................................................................................................ 61 3.4.1 Critical Values of Bivariate Functions.......................................................................................... 61 3.4.2. Critical Points of Multivariate Functions...................................................................................... 64 3.4.3. Constrained Optimisation ............................................................................................................. 67 4 INTEGRAL CALCULUS........................................................................................................................... 72 4.1. INTEGRATION.......................................................................................................................................... 72 2 4.1.1. Definite and Indefinite Integrals ................................................................................................... 72 4.1.2. Properties of definite integrals...................................................................................................... 74 4.1.3. Rules of Integration - Indefinite Integral ...................................................................................... 75 4.1.4. Auxiliary Conditions..................................................................................................................... 79 4.2. APPLICATIONS OF INTEGRALS ................................................................................................................. 79 4.2.1. Deriving Totals (Revenue/Cost) from Marginals (Revenue/Cost)................................................ 79 4.2.2. Present Value of Cashflows.......................................................................................................... 80 4.2.3. Measuring Probabilities ................................................................................................................ 81 4.3 MULTIPLE INTEGRATION......................................................................................................................... 81 4.3.1. Double Integral of a Function of Two Variables ..........................................................................81
Load more

Recommended publications
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • Antiderivatives and the Area Problem
    Chapter 7 antiderivatives and the area problem Let me begin by defining the terms in the title: 1. an antiderivative of f is another function F such that F 0 = f. 2. the area problem is: ”find the area of a shape in the plane" This chapter is concerned with understanding the area problem and then solving it through the fundamental theorem of calculus(FTC). We begin by discussing antiderivatives. At first glance it is not at all obvious this has to do with the area problem. However, antiderivatives do solve a number of interesting physical problems so we ought to consider them if only for that reason. The beginning of the chapter is devoted to understanding the type of question which an antiderivative solves as well as how to perform a number of basic indefinite integrals. Once all of this is accomplished we then turn to the area problem. To understand the area problem carefully we'll need to think some about the concepts of finite sums, se- quences and limits of sequences. These concepts are quite natural and we will see that the theory for these is easily transferred from some of our earlier work. Once the limit of a sequence and a number of its basic prop- erties are established we then define area and the definite integral. Finally, the remainder of the chapter is devoted to understanding the fundamental theorem of calculus and how it is applied to solve definite integrals. I have attempted to be rigorous in this chapter, however, you should understand that there are superior treatments of integration(Riemann-Stieltjes, Lesbeque etc..) which cover a greater variety of functions in a more logically complete fashion.
    [Show full text]
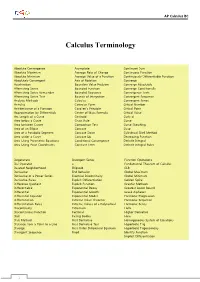
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Notes Chapter 4(Integration) Definition of an Antiderivative
    1 Notes Chapter 4(Integration) Definition of an Antiderivative: A function F is an antiderivative of f on an interval I if for all x in I. Representation of Antiderivatives: If F is an antiderivative of f on an interval I, then G is an antiderivative of f on the interval I if and only if G is of the form G(x) = F(x) + C, for all x in I where C is a constant. Sigma Notation: The sum of n terms a1,a2,a3,…,an is written as where I is the index of summation, ai is the ith term of the sum, and the upper and lower bounds of summation are n and 1. Summation Formulas: 1. 2. 3. 4. Limits of the Lower and Upper Sums: Let f be continuous and nonnegative on the interval [a,b]. The limits as n of both the lower and upper sums exist and are equal to each other. That is, where are the minimum and maximum values of f on the subinterval. Definition of the Area of a Region in the Plane: Let f be continuous and nonnegative on the interval [a,b]. The area if a region bounded by the graph of f, the x-axis and the vertical lines x=a and x=b is Area = where . Definition of a Riemann Sum: Let f be defined on the closed interval [a,b], and let be a partition of [a,b] given by a =x0<x1<x2<…<xn-1<xn=b where xi is the width of the ith subinterval.
    [Show full text]
  • 4.1 AP Calc Antiderivatives and Indefinite Integration.Notebook November 28, 2016
    4.1 AP Calc Antiderivatives and Indefinite Integration.notebook November 28, 2016 4.1 Antiderivatives and Indefinite Integration Learning Targets 1. Write the general solution of a differential equation 2. Use indefinite integral notation for antiderivatives 3. Use basic integration rules to find antiderivatives 4. Find a particular solution of a differential equation 5. Plot a slope field 6. Working backwards in physics Intro/Warm­up 1 4.1 AP Calc Antiderivatives and Indefinite Integration.notebook November 28, 2016 Note: I am changing up the procedure of the class! When you walk in the class, you will put a tally mark on those problems that you would like me to go over, and you will turn in your homework with your name, the section and the page of the assignment. Order of the day 2 4.1 AP Calc Antiderivatives and Indefinite Integration.notebook November 28, 2016 Vocabulary First, find a function F whose derivative is . because any other function F work? So represents the family of all antiderivatives of . The constant C is called the constant of integration. The family of functions represented by F is the general antiderivative of f, and is the general solution to the differential equation The operation of finding all solutions to the differential equation is called antidifferentiation (or indefinite integration) and is denoted by an integral sign: is read as the antiderivative of f with respect to x. Vocabulary 3 4.1 AP Calc Antiderivatives and Indefinite Integration.notebook November 28, 2016 Nov 28­9:38 AM 4 4.1 AP Calc Antiderivatives and Indefinite Integration.notebook November 28, 2016 ∫ Use basic integration rules to find antiderivatives The Power Rule: where 1.
    [Show full text]
  • Newton and Halley Are One Step Apart
    Methods for Solving Nonlinear Equations Local Methods for Unconstrained Optimization The General Sparsity of the Third Derivative How to Utilize Sparsity in the Problem Numerical Results Newton and Halley are one step apart Trond Steihaug Department of Informatics, University of Bergen, Norway 4th European Workshop on Automatic Differentiation December 7 - 8, 2006 Institute for Scientific Computing RWTH Aachen University Aachen, Germany (This is joint work with Geir Gundersen) Trond Steihaug Newton and Halley are one step apart Methods for Solving Nonlinear Equations Local Methods for Unconstrained Optimization The General Sparsity of the Third Derivative How to Utilize Sparsity in the Problem Numerical Results Overview - Methods for Solving Nonlinear Equations: Method in the Halley Class is Two Steps of Newton in disguise. - Local Methods for Unconstrained Optimization. - How to Utilize Structure in the Problem. - Numerical Results. Trond Steihaug Newton and Halley are one step apart Methods for Solving Nonlinear Equations Local Methods for Unconstrained Optimization The Halley Class The General Sparsity of the Third Derivative Motivation How to Utilize Sparsity in the Problem Numerical Results Newton and Halley A central problem in scientific computation is the solution of system of n equations in n unknowns F (x) = 0 n n where F : R → R is sufficiently smooth. Sir Isaac Newton (1643 - 1727). Sir Edmond Halley (1656 - 1742). Trond Steihaug Newton and Halley are one step apart Methods for Solving Nonlinear Equations Local Methods for Unconstrained Optimization The Halley Class The General Sparsity of the Third Derivative Motivation How to Utilize Sparsity in the Problem Numerical Results A Nonlinear Newton method Taylor expansion 0 1 00 T (s) = F (x) + F (x)s + F (x)ss 2 Nonlinear Newton: Given x.
    [Show full text]
  • 12.4 Calculus Review
    Appendix 445 12.4 Calculus review This section is a very brief summary of Calculus skills required for reading this book. 12.4.1 Inverse function Function g is the inverse function of function f if g(f(x)) = x and f(g(y)) = y for all x and y where f(x) and g(y) exist. 1 Notation Inverse function g = f − 1 (Don’t confuse the inverse f − (x) with 1/f(x). These are different functions!) To find the inverse function, solve the equation f(x) = y. The solution g(y) is the inverse of f. For example, to find the inverse of f(x)=3+1/x, we solve the equation 1 3 + 1/x = y 1/x = y 3 x = . ⇒ − ⇒ y 3 − The inverse function of f is g(y) = 1/(y 3). − 12.4.2 Limits and continuity A function f(x) has a limit L at a point x0 if f(x) approaches L when x approaches x0. To say it more rigorously, for any ε there exists such δ that f(x) is ε-close to L when x is δ-close to x0. That is, if x x < δ then f(x) L < ε. | − 0| | − | A function f(x) has a limit L at + if f(x) approaches L when x goes to + . Rigorously, for any ε there exists such N that f∞(x) is ε-close to L when x gets beyond N∞, i.e., if x > N then f(x) L < ε. | − | Similarly, f(x) has a limit L at if for any ε there exists such N that f(x) is ε-close to L when x gets below ( N), i.e.,−∞ − if x < N then f(x) L < ε.
    [Show full text]
  • 1. Antiderivatives for Exponential Functions Recall That for F(X) = Ec⋅X, F ′(X) = C ⋅ Ec⋅X (For Any Constant C)
    1. Antiderivatives for exponential functions Recall that for f(x) = ec⋅x, f ′(x) = c ⋅ ec⋅x (for any constant c). That is, ex is its own derivative. So it makes sense that it is its own antiderivative as well! Theorem 1.1 (Antiderivatives of exponential functions). Let f(x) = ec⋅x for some 1 constant c. Then F x ec⋅c D, for any constant D, is an antiderivative of ( ) = c + f(x). 1 c⋅x ′ 1 c⋅x c⋅x Proof. Consider F (x) = c e +D. Then by the chain rule, F (x) = c⋅ c e +0 = e . So F (x) is an antiderivative of f(x). Of course, the theorem does not work for c = 0, but then we would have that f(x) = e0 = 1, which is constant. By the power rule, an antiderivative would be F (x) = x + C for some constant C. 1 2. Antiderivative for f(x) = x We have the power rule for antiderivatives, but it does not work for f(x) = x−1. 1 However, we know that the derivative of ln(x) is x . So it makes sense that the 1 antiderivative of x should be ln(x). Unfortunately, it is not. But it is close. 1 1 Theorem 2.1 (Antiderivative of f(x) = x ). Let f(x) = x . Then the antiderivatives of f(x) are of the form F (x) = ln(SxS) + C. Proof. Notice that ln(x) for x > 0 F (x) = ln(SxS) = . ln(−x) for x < 0 ′ 1 For x > 0, we have [ln(x)] = x .
    [Show full text]
  • Calculus Online Textbook Chapter 2
    Contents CHAPTER 1 Introduction to Calculus 1.1 Velocity and Distance 1.2 Calculus Without Limits 1.3 The Velocity at an Instant 1.4 Circular Motion 1.5 A Review of Trigonometry 1.6 A Thousand Points of Light 1.7 Computing in Calculus CHAPTER 2 Derivatives The Derivative of a Function Powers and Polynomials The Slope and the Tangent Line Derivative of the Sine and Cosine The Product and Quotient and Power Rules Limits Continuous Functions CHAPTER 3 Applications of the Derivative 3.1 Linear Approximation 3.2 Maximum and Minimum Problems 3.3 Second Derivatives: Minimum vs. Maximum 3.4 Graphs 3.5 Ellipses, Parabolas, and Hyperbolas 3.6 Iterations x, + ,= F(x,) 3.7 Newton's Method and Chaos 3.8 The Mean Value Theorem and l'H8pital's Rule CHAPTER 2 Derivatives 2.1 The Derivative of a Function This chapter begins with the definition of the derivative. Two examples were in Chapter 1. When the distance is t2, the velocity is 2t. When f(t) = sin t we found v(t)= cos t. The velocity is now called the derivative off (t). As we move to a more formal definition and new examples, we use new symbols f' and dfldt for the derivative. 2A At time t, the derivativef'(t)or df /dt or v(t) is fCt -t At) -f (0 f'(t)= lim (1) At+O At The ratio on the right is the average velocity over a short time At. The derivative, on the left side, is its limit as the step At (delta t) approaches zero.
    [Show full text]
  • Antiderivatives Math 121 Calculus II D Joyce, Spring 2013
    Antiderivatives Math 121 Calculus II D Joyce, Spring 2013 Antiderivatives and the constant of integration. We'll start out this semester talking about antiderivatives. If the derivative of a function F isf, that is, F 0 = f, then we say F is an antiderivative of f. Of course, antiderivatives are important in solving problems when you know a derivative but not the function, but we'll soon see that lots of questions involving areas, volumes, and other things also come down to finding antiderivatives. That connection we'll see soon when we study the Fundamental Theorem of Calculus (FTC). For now, we'll just stick to the basic concept of antiderivatives. We can find antiderivatives of polynomials pretty easily. Suppose that we want to find an antiderivative F (x) of the polynomial f(x) = 4x3 + 5x2 − 3x + 8: We can find one by finding an antiderivative of each term and adding the results together. Since the derivative of x4 is 4x3, therefore an antiderivative of 4x3 is x4. It's not much harder to find an antiderivative of 5x2. Since the derivative of x3 is 3x2, an antiderivative of 5x2 is 5 3 3 x . Continue on and soon you see that an antiderivative of f(x) is 4 5 3 3 2 F (x) = x + 3 x − 2 x + 8x: There are, however, other antiderivatives of f(x). Since the derivative of a constant is 0, 4 5 3 3 2 we can add any constant to F (x) to find another antiderivative. Thus, x + 3 x − 2 x +8x+7 4 5 3 3 2 is another antiderivative of f(x).
    [Show full text]
  • Derivatives and Antiderivatives
    Lesson R MA 16020 Nick Egbert Note. There should be no new information in this lesson. This is a brief review of things you should have learned in Calculus I, but certainly not exhaustive. Derivatives and antiderivatives There are several derivative anti derivative rules that you should have pretty well-memorized at this point: It is very important that you know these well to make the transition into this course go smoothly. Definition. Given a continuous function f(x), if F 0(x) = f(x); we say that F (x) is an antiderivative of f(x); and we write Z F (x) = f(x) dx: 1 Lesson R MA 16020 Nick Egbert Remark. If F (x) is an antiderivative of f(x) then the indefinite integral of f is given by Z f(x) dx = F (x) + C; where C is some constant. This means that any two functions which differ by only a constant will have the same antiderivative. Remark. We want to note a couple things about the notation R f(x)dx: 1. The process of computing R f(x)dx can be called antidifferentiation 5 integration 5 taking or evaluating the integral 2. f(5x) is called the integrand. 3. Writing the \dx" on the outside is essential. This tells us that we are integrating with respect to x. It will especially be important in MA 16020 when we start having integrals with more than one variable. Fundamental theorem of calculus Theorem. If f is a real-valued continuous function on the interval [a; b]; and F the antiderivative of f: Z x F (x) = f(t) dt; a Then F 0(x) = f(x) for all x in the interval (a; b): In particular, we have that Z b f(t) dt = F (b) − F (a): a This has an important geometric interpretation.
    [Show full text]
  • Multiple Integrals
    Chapter 11 Multiple Integrals 11.1 Double Riemann Sums and Double Integrals over Rectangles Motivating Questions In this section, we strive to understand the ideas generated by the following important questions: What is a double Riemann sum? • How is the double integral of a continuous function f = f(x; y) defined? • What are two things the double integral of a function can tell us? • Introduction In single-variable calculus, recall that we approximated the area under the graph of a positive function f on an interval [a; b] by adding areas of rectangles whose heights are determined by the curve. The general process involved subdividing the interval [a; b] into smaller subintervals, constructing rectangles on each of these smaller intervals to approximate the region under the curve on that subinterval, then summing the areas of these rectangles to approximate the area under the curve. We will extend this process in this section to its three-dimensional analogs, double Riemann sums and double integrals over rectangles. Preview Activity 11.1. In this activity we introduce the concept of a double Riemann sum. (a) Review the concept of the Riemann sum from single-variable calculus. Then, explain how R b we define the definite integral a f(x) dx of a continuous function of a single variable x on an interval [a; b]. Include a sketch of a continuous function on an interval [a; b] with appropriate labeling in order to illustrate your definition. (b) In our upcoming study of integral calculus for multivariable functions, we will first extend 181 182 11.1.
    [Show full text]