DOCSLIB.ORG

7. Cratering on Mars

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
7. Cratering on Mars 7. Cratering on Mars Impact cratering is one of the fundamen- 1987; Holsapple and Schmidt, 1987; Schmidt tal geological processes, and is visible on ev- and Housen, 1987; Croft, 1985b,a; O’Keefe and ery solid surface body in the solar system (e.g. Ahrens, 1981). The cratering process is con- Alfred Wegener, 1921). When the disrupted trolled by the target strength and for larger im- comet Shoemaker–Levi–9 hit Jupiter, it was pacting bodies by the surface gravity (Schmidt the only and the most spectacular opportu- and Housen, 1987). The final crater diameter nity to observe an impact event, but it left and appearance depends on gravity and mate- just short–term turbulences in the Jovian atmo- rial parameters (Croft, 1985b,a). Besides the sphere. On solid surfaces the impacting projec- knowledge of impact mechanism, other obvi- tiles form bowl–shaped depressions, which are ous differences in the impact environment in- named craters after a certain type of ancient fluences the final crater form, i.e. surface grav- Greek vase. Depending on the impacting en- ity, impact velocity, the presence of atmosphere ergy the crater morphology changes with diam- and the probable abundance of water or ice in eter. This progression was already described by the Martian subsurface. Gilbert in 1893. Mariner 9 images have revealed a diverse 7.1. Cratering Mechanics range of morphology and ejecta characteris- tics and potential target differences (Arvidson Independent of the final crater size, the process et al., 1976; McCauley, 1973). Impact crater of impact cratering always follows a three stage morphology and especially ejecta are largely scheme, which has been described in detail by unique to Mars (although they are found on Melosh (1989). The three stages of the impact the jovian moon Europa and on Earth). They cratering process are (1) contact and compres- have probably been strongly influenced by sub- sion, (2) excavation, and (3) modification (Fig. surface volatiles and are widespread through- 7.1). out the surface of the planet. The Martian im- During the first stage, the projectile contacts pact record in terms of crater morphology, mor- the target. As it hits, the target is instan- phometry, modification and crater frequency taneously compressed and accelerated, while has been catalogued by Strom et al. (1992), but the projectile itself is decelerated by the resis- their study also revealed the difficulties in the tance of the target. A shock wave originates at fundamental morphologic classification. Keys the point of contact and travels through target to explaining the large variety of central crater and projectile, producing pressures much larger structures or ejecta blankets include the geo- than the yield strength of either the target or logical conditions of the surface and subsurface the projectile. This stage, lasting a ”blink of an (possibly the atmosphere as well). The depen- eye”, ends after the shock wave has passed. dence of crater diameter on the condition of im- The second stage is divided into the expan- pacts, defined by the impacting body (radius, sion of the shock wave and the excavation flow. mass, density, impact velocity) and the plane- While the shock wave expands hemispherically tary surface (surface gravity, density, strength) (and subsequently degrades to a stress wave), is generally estimated by a form of scaling that the target material is set into motion radially employs both theory and small scale measure- away from the impact site (immediately behind ments to extrapolate to the large scales of ob- the shock wave). Rarefaction waves create an served craters and impact basins (Holsapple, upward–directed pressure gradient behind the 31 32 Cratering on Mars shock wave. This additional upward compo- nent to the radial velocity initializes the exca- vation flow and the largest portion of material ejects from the crater. This ejected material follows purely ballistic trajectories, the ejecta curtain. Material ejected first, closest to the impact site, has the highest velocities, and con- sequently takes the longest to fall. The growth of a crater up to the transient cavity starts as a hemispherical expansion following the shock wave until the final depth is achieved. Due to less resistance at the surface the crater diameter continues to grow further until its final diameter is achieved (Fig. 7.1). This state of the crater is called transient cavity. The final observed rim– to–rim diameter is different from the transient diameter and is reached in the last, so–called modification stage. During the final modification stage, the ejected debris is finally deposited and the crater interior becomes modified. The fundamental Figure 7.1.: The growth of a crater: The crater idea of ejecta emplacement is that the ejected first opens following the hemispherical expansion of material travels in a near parabolic trajec- the shock wave (a). The growth rate is steadily tory as a so–called ejecta curtain (ballistically). decreasing due to the resistance of the underlying Based on observations, one expects very lit- target rocks until its maximum depth is achieved tle material to escape the gravitational field (b). Less resistance at surface let the crater di- of a planet, most falling back to the surface ameter continue to grow (c) and stops when no and forming a continuous ejecta blanket sur- more material is ejected. The resulting transient crater is broader than a hemisphere (d) (Fig. from rounding the crater. The innermost ejecta are Melosh (1989)). Depending of the size of the tran- launched first, travel fastest and can reach long sient crater, modification in the given gravity field distances. Ejecta originating farther from the results in different morphologies. center are launched later, moving more slowly and falling sooner and closer to the rim. Only material from the uppermost third to half of the depth of the transient crater is excavated can be found, which are formed by large chunks from the crater. Target material deeper than of material during the excavation period. On the maximum excavation depth has been dis- the Moon, secondary craters can reach a size placed beneath the crater floor. The maximum of about 4% the diameter of the primary im- excavation depth (and the strata represented pact crater. The secondary crater itself is not in the ejecta blanket) is considerably shallower necessarily distinguishable on the basis of its than the maximum crater depth. Close to the morphology (they could appear more elliptical), rim, material is deposited in reversed origi- but ejecta of secondaries have a characteristic nal stratigraphy (overturned flap, Roddy et al. V–shaped ridge pointing radially away from the (1975)). The continuous ejecta blanket covers main crater. Cluster or chain formation also an area of roughly one crater radius from the help to identify them. Lined up as a chain, the crater rim, followed by a thin and patchy unit. chevron pattern turns into a herringbone pat- In the latter unit and beyond, secondary craters tern (Oberbeck and Morrison, 1973). In gen- Impact Crater Morphologies 33 eral, these crater–field forms are all strongly behavior of the impact cratering event. These controlled by the gravity field of the planet. experiments are limited in reproducing the ef- The change of the crater interior during the fects of high–energy impacts, which involve ex- modification stage varies, depending upon the treme pressures, temperatures and large crater– size of the transient cavity, and the shape char- diameter range (role of gravity during the for- acteristic of simple or progressively complex im- mation of large craters). Therefore, computer pact craters. For small craters, forming a final simulations are the only feasible method to simple bowl–shaped crater, the transient cav- study large–scale impact events. The complex- ity is filled by material falling back from the ity of the process involved during the crater for- unstable rim to subsequently fill the center of mation, especially the passage of shock waves the crater (wall slumping, Moore (1976)). The and the irreversible behavior of geologic ma- larger an impact crater, the further the ini- terial are translated into computer codes that tial transient departs from gravitational stabil- handle the shock wave propagation (velocities, ity and is modified more strongly during this stresses and strains) as a function of time and last crater forming stage. position. These are called hydrodynamical computer codes (”hydrocodes”). These codes 7.2. Crater Modeling are based on a discretized particle motion es- tablished through the principles of conserva- Currently, the applied crater size–frequency tion of momentum, mass and energy from a distribution is based on the transferred lunar macroscopic point of view (Anderson, 1987), curve. This transfer procedure is outlined in the equation–of–state, relating pressure, den- Section 5 and discussed in detail by Neukum sity and the specific internal energy (needed and Ivanov (1994); Ivanov (2001). To fur- to describe compressibility effects and irre- ther refine and verify the modeling and trans- versible thermodynamic processes), and a rhe- fer of the Martian crater production function, ology (constitutive) model, which describes the pre–existing modeling efforts have been contin- response of a material to deformation (change ued by refining existing scaling laws, improv- in shape or strength properties). ing models for crater collapse, and estimat- One of the most important issues concerning ing the impacting flux of planetesimals, includ- hydrocodes is the description of the discontin- ing comets (Ivanov, 2001). Target parameters uous nature of shock waves, which may intro- such as subsurface water, sedimentary and vol- duce instabilities in the discretized representa- canic rocks of different water or ice saturation tion. The choice of a discretization approach stages lead to a variety of scenarios that in- and solving methods depends on the problem fluence the final crater diameter, and there- to be solved, so a variety of hydrocodes have fore deviate from the analytical Martian crater been developed.
Load more

Recommended publications
  • Curiosity's Candidate Field Site in Gale Crater, Mars
    Curiosity’s Candidate Field Site in Gale Crater, Mars K. S. Edgett – 27 September 2010 Simulated view from Curiosity rover in landing ellipse looking toward the field area in Gale; made using MRO CTX stereopair images; no vertical exaggeration. The mound is ~15 km away 4th MSL Landing Site Workshop, 27–29 September 2010 in this view. Note that one would see Gale’s SW wall in the distant background if this were Edgett, 1 actually taken by the Mastcams on Mars. Gale Presents Perhaps the Thickest and Most Diverse Exposed Stratigraphic Section on Mars • Gale’s Mound appears to present the thickest and most diverse exposed stratigraphic section on Mars that we can hope access in this decade. • Mound has ~5 km of stratified rock. (That’s 3 miles!) • There is no evidence that volcanism ever occurred in Gale. • Mound materials were deposited as sediment. • Diverse materials are present. • Diverse events are recorded. – Episodes of sedimentation and lithification and diagenesis. – Episodes of erosion, transport, and re-deposition of mound materials. 4th MSL Landing Site Workshop, 27–29 September 2010 Edgett, 2 Gale is at ~5°S on the “north-south dichotomy boundary” in the Aeolis and Nepenthes Mensae Region base map made by MSSS for National Geographic (February 2001); from MOC wide angle images and MOLA topography 4th MSL Landing Site Workshop, 27–29 September 2010 Edgett, 3 Proposed MSL Field Site In Gale Crater Landing ellipse - very low elevation (–4.5 km) - shown here as 25 x 20 km - alluvium from crater walls - drive to mound Anderson & Bell
    [Show full text]
  • Supervolcanoes Within an Ancient Volcanic Province in Arabia Terra, Mars 2 3 4 Joseph
    EMBARGOED BY NATURE 1 1 Supervolcanoes within an ancient volcanic province in Arabia Terra, Mars 2 3 4 Joseph. R. Michalski 1,2 5 1Planetary Science Institute, Tucson, Arizona 85719, [email protected] 6 2Dept. of Earth Sciences, Natural History Museum, London, United Kingdom 7 8 Jacob E. Bleacher3 9 3NASA Goddard Space Flight Center, Greenbelt, MD, USA. 10 11 12 Summary: 13 14 Several irregularly shaped craters located within Arabia Terra, Mars represent a 15 new type of highland volcanic construct and together constitute a previously 16 unrecognized martian igneous province. Similar to terrestrial supervolcanoes, these 17 low-relief paterae display a range of geomorphic features related to structural 18 collapse, effusive volcanism, and explosive eruptions. Extruded lavas contributed to 19 the formation of enigmatic highland ridged plains in Arabia Terra. Outgassed sulfur 20 and erupted fine-grained pyroclastics from these calderas likely fed the formation of 21 altered, layered sedimentary rocks and fretted terrain found throughout the 22 equatorial region. Discovery of a new type of volcanic construct in the Arabia 23 volcanic province fundamentally changes the picture of ancient volcanism and 24 climate evolution on Mars. Other eroded topographic basins in the ancient Martian 25 highlands that have been dismissed as degraded impact craters should be 26 reconsidered as possible volcanic constructs formed in an early phase of 27 widespread, disseminated magmatism on Mars. 28 29 30 EMBARGOED BY NATURE 2 31 The source of fine-grained, layered deposits1,2 detected throughout the equatorial 32 region of Mars3 remains unresolved, though the deposits are clearly linked to global 33 sedimentary processes, climate change, and habitability of the surface4.
    [Show full text]
  • Minutes of the January 25, 2010, Meeting of the Board of Regents
    MINUTES OF THE JANUARY 25, 2010, MEETING OF THE BOARD OF REGENTS ATTENDANCE This scheduled meeting of the Board of Regents was held on Monday, January 25, 2010, in the Regents’ Room of the Smithsonian Institution Castle. The meeting included morning, afternoon, and executive sessions. Board Chair Patricia Q. Stonesifer called the meeting to order at 8:31 a.m. Also present were: The Chief Justice 1 Sam Johnson 4 John W. McCarter Jr. Christopher J. Dodd Shirley Ann Jackson David M. Rubenstein France Córdova 2 Robert P. Kogod Roger W. Sant Phillip Frost 3 Doris Matsui Alan G. Spoon 1 Paul Neely, Smithsonian National Board Chair David Silfen, Regents’ Investment Committee Chair 2 Vice President Joseph R. Biden, Senators Thad Cochran and Patrick J. Leahy, and Representative Xavier Becerra were unable to attend the meeting. Also present were: G. Wayne Clough, Secretary John Yahner, Speechwriter to the Secretary Patricia L. Bartlett, Chief of Staff to the Jeffrey P. Minear, Counselor to the Chief Justice Secretary T.A. Hawks, Assistant to Senator Cochran Amy Chen, Chief Investment Officer Colin McGinnis, Assistant to Senator Dodd Virginia B. Clark, Director of External Affairs Kevin McDonald, Assistant to Senator Leahy Barbara Feininger, Senior Writer‐Editor for the Melody Gonzales, Assistant to Congressman Office of the Regents Becerra Grace L. Jaeger, Program Officer for the Office David Heil, Assistant to Congressman Johnson of the Regents Julie Eddy, Assistant to Congresswoman Matsui Richard Kurin, Under Secretary for History, Francisco Dallmeier, Head of the National Art, and Culture Zoological Park’s Center for Conservation John K.
    [Show full text]
  • Analogue Sites for Mars Missions: MSL and Beyond
    Program and Abstract Volume LPI Contribution No. 1612 Analogue Sites for Mars Missions: MSL and Beyond March 5–6, 2011 • The Woodlands, Texas Sponsors National Aeronautics and Space Administration Lunar and Planetary Institute Conveners Mary Voytek, NASA Headquarters Michael Meyer, NASA Headquarters Victoria Hipkin, Canadian Space Agency Richard Leveille, Canadian Space Agency Shawn Domagal-Goldman, NASA Headquarters Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 LPI Contribution No. 1612 Compiled in 2011 by Meeting and Publication Services Lunar and Planetary Institute USRA Houston 3600 Bay Area Boulevard, Houston TX 77058-1113 The Lunar and Planetary Institute is operated by the Universities Space Research Association under a cooperative agreement with the Science Mission Directorate of the National Aeronautics and Space Administration. Any opinions, findings, and conclusions or recommendations expressed in this volume are those of the author(s) and do not necessarily reflect the views of the National Aeronautics and Space Administration. Material in this volume may be copied without restraint for library, abstract service, education, or personal research purposes; however, republication of any paper or portion thereof requires the written permission of the authors as well as the appropriate acknowledgment of this publication. Abstracts in this volume may be cited as Author A. B. (2011) Title of abstract. In Analogue Sites for Mars Missions: MSL and Beyond, p. XX. LPI Contribution No. 1612, Lunar and Planetary Institute, Houston. ISSN No. 0161-5297 Preface This volume contains abstracts that have been accepted for presentation at the workshop on Analogue Sites for Mars Missions: MSL and Beyond, March 5–6, 2011, The Woodlands, Texas.
    [Show full text]
  • MARS an Overview of the 1985–2006 Mars Orbiter Camera Science
    MARS MARS INFORMATICS The International Journal of Mars Science and Exploration Open Access Journals Science An overview of the 1985–2006 Mars Orbiter Camera science investigation Michael C. Malin1, Kenneth S. Edgett1, Bruce A. Cantor1, Michael A. Caplinger1, G. Edward Danielson2, Elsa H. Jensen1, Michael A. Ravine1, Jennifer L. Sandoval1, and Kimberley D. Supulver1 1Malin Space Science Systems, P.O. Box 910148, San Diego, CA, 92191-0148, USA; 2Deceased, 10 December 2005 Citation: Mars 5, 1-60, 2010; doi:10.1555/mars.2010.0001 History: Submitted: August 5, 2009; Reviewed: October 18, 2009; Accepted: November 15, 2009; Published: January 6, 2010 Editor: Jeffrey B. Plescia, Applied Physics Laboratory, Johns Hopkins University Reviewers: Jeffrey B. Plescia, Applied Physics Laboratory, Johns Hopkins University; R. Aileen Yingst, University of Wisconsin Green Bay Open Access: Copyright 2010 Malin Space Science Systems. This is an open-access paper distributed under the terms of a Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract Background: NASA selected the Mars Orbiter Camera (MOC) investigation in 1986 for the Mars Observer mission. The MOC consisted of three elements which shared a common package: a narrow angle camera designed to obtain images with a spatial resolution as high as 1.4 m per pixel from orbit, and two wide angle cameras (one with a red filter, the other blue) for daily global imaging to observe meteorological events, geodesy, and provide context for the narrow angle images. Following the loss of Mars Observer in August 1993, a second MOC was built from flight spare hardware and launched aboard Mars Global Surveyor (MGS) in November 1996.
    [Show full text]
  • Martian Crater Morphology
    ANALYSIS OF THE DEPTH-DIAMETER RELATIONSHIP OF MARTIAN CRATERS A Capstone Experience Thesis Presented by Jared Howenstine Completion Date: May 2006 Approved By: Professor M. Darby Dyar, Astronomy Professor Christopher Condit, Geology Professor Judith Young, Astronomy Abstract Title: Analysis of the Depth-Diameter Relationship of Martian Craters Author: Jared Howenstine, Astronomy Approved By: Judith Young, Astronomy Approved By: M. Darby Dyar, Astronomy Approved By: Christopher Condit, Geology CE Type: Departmental Honors Project Using a gridded version of maritan topography with the computer program Gridview, this project studied the depth-diameter relationship of martian impact craters. The work encompasses 361 profiles of impacts with diameters larger than 15 kilometers and is a continuation of work that was started at the Lunar and Planetary Institute in Houston, Texas under the guidance of Dr. Walter S. Keifer. Using the most ‘pristine,’ or deepest craters in the data a depth-diameter relationship was determined: d = 0.610D 0.327 , where d is the depth of the crater and D is the diameter of the crater, both in kilometers. This relationship can then be used to estimate the theoretical depth of any impact radius, and therefore can be used to estimate the pristine shape of the crater. With a depth-diameter ratio for a particular crater, the measured depth can then be compared to this theoretical value and an estimate of the amount of material within the crater, or fill, can then be calculated. The data includes 140 named impact craters, 3 basins, and 218 other impacts. The named data encompasses all named impact structures of greater than 100 kilometers in diameter.
    [Show full text]
  • Program and Abstracts of 2017 Congress / Programme Et Résumés
    1 Sponsors | Commanditaires Gold Sponsors | Commanditaires d’or Silver Sponsors | Commanditaires d’argent Other Sponsors | Les autres Commanditaires 2 Contents Sponsors | Commanditaires .......................................................................................................................... 2 Welcome from the Premier of Ontario .......................................................................................................... 5 Bienvenue du premier ministre de l'Ontario .................................................................................................. 6 Welcome from the Mayor of Toronto ............................................................................................................ 7 Mot de bienvenue du maire de Toronto ........................................................................................................ 8 Welcome from the Minister of Fisheries, Oceans and the Canadian Coast Guard ...................................... 9 Mot de bienvenue de ministre des Pêches, des Océans et de la Garde côtière canadienne .................... 10 Welcome from the Minister of Environment and Climate Change .............................................................. 11 Mot de bienvenue du Ministre d’Environnement et Changement climatique Canada ................................ 12 Welcome from the President of the Canadian Meteorological and Oceanographic Society ...................... 13 Mot de bienvenue du président de la Société canadienne de météorologie et d’océanographie .............
    [Show full text]
  • Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography on the Occasion of the 50Th Anniversary of Apollo 11 Moon Landing
    Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography On the occasion of the 50th anniversary of Apollo 11 moon landing Please note: A specific item in this catalogue may be sold or is on hold if the provided link to our online inventory (by clicking on the blue-highlighted author name) doesn't work! Milestones of Science Books phone +49 (0) 177 – 2 41 0006 www.milestone-books.de [email protected] Member of ILAB and VDA Catalogue 07-2019 Copyright © 2019 Milestones of Science Books. All rights reserved Page 2 of 71 Authors in Chronological Order Author Year No. Author Year No. BIRT, William 1869 7 SCHEINER, Christoph 1614 72 PROCTOR, Richard 1873 66 WILKINS, John 1640 87 NASMYTH, James 1874 58, 59, 60, 61 SCHYRLEUS DE RHEITA, Anton 1645 77 NEISON, Edmund 1876 62, 63 HEVELIUS, Johannes 1647 29 LOHRMANN, Wilhelm 1878 42, 43, 44 RICCIOLI, Giambattista 1651 67 SCHMIDT, Johann 1878 75 GALILEI, Galileo 1653 22 WEINEK, Ladislaus 1885 84 KIRCHER, Athanasius 1660 31 PRINZ, Wilhelm 1894 65 CHERUBIN D'ORLEANS, Capuchin 1671 8 ELGER, Thomas Gwyn 1895 15 EIMMART, Georg Christoph 1696 14 FAUTH, Philipp 1895 17 KEILL, John 1718 30 KRIEGER, Johann 1898 33 BIANCHINI, Francesco 1728 6 LOEWY, Maurice 1899 39, 40 DOPPELMAYR, Johann Gabriel 1730 11 FRANZ, Julius Heinrich 1901 21 MAUPERTUIS, Pierre Louis 1741 50 PICKERING, William 1904 64 WOLFF, Christian von 1747 88 FAUTH, Philipp 1907 18 CLAIRAUT, Alexis-Claude 1765 9 GOODACRE, Walter 1910 23 MAYER, Johann Tobias 1770 51 KRIEGER, Johann 1912 34 SAVOY, Gaspare 1770 71 LE MORVAN, Charles 1914 37 EULER, Leonhard 1772 16 WEGENER, Alfred 1921 83 MAYER, Johann Tobias 1775 52 GOODACRE, Walter 1931 24 SCHRÖTER, Johann Hieronymus 1791 76 FAUTH, Philipp 1932 19 GRUITHUISEN, Franz von Paula 1825 25 WILKINS, Hugh Percy 1937 86 LOHRMANN, Wilhelm Gotthelf 1824 41 USSR ACADEMY 1959 1 BEER, Wilhelm 1834 4 ARTHUR, David 1960 3 BEER, Wilhelm 1837 5 HACKMAN, Robert 1960 27 MÄDLER, Johann Heinrich 1837 49 KUIPER Gerard P.
    [Show full text]
  • Widespread Excess Ice in Arcadia Planitia, Mars
    Widespread Excess Ice in Arcadia Planitia, Mars Ali M. Bramson1, Shane Byrne1, Nathaniel E. Putzig2, Sarah Sutton1, Jeffrey J. Plaut3, T. Charles Brothers4 and John W. Holt4 Corresponding author: A. M. Bramson, Lunar and Planetary Laboratory, University of Arizona, Kuiper Space Science Building, 1629 E. University Blvd. Tucson, AZ, 85721, USA. ([email protected]) Affiliations: 1Lunar and Planetary Laboratory, University of Arizona, Tucson, Arizona, USA. 2Southwest Research Institute, Boulder, Colorado, USA. 3Jet Propulsion Laboratory, Pasadena, California, USA. 4Institute for Geophysics, University of Texas at Austin, Austin, Texas, USA. Accepted for publication July 18, 2015 in Geophysical Research Letters. An edited version of this paper was published by AGU on August 26, 2015. Copyright 2015 American Geophysical Union. Citation: Bramson, A. M., S. Byrne, N. E. Putzig, S. Sutton, J. J. Plaut, T. C. Brothers, and J. W. Holt (2015), Widespread excess ice in Arcadia Planitia, Mars, Geophys. Res. Lett., 42, doi:10.1002/2015GL064844. Key points: • Terraced craters: abundant in Arcadia Planitia, indicate subsurface layering • A widespread subsurface interface is also detected by SHARAD • Combining data sets yields dielectric constants consistent with decameters of excess water ice Abstract: The distribution of subsurface water ice on Mars is a key constraint on past climate, while the volumetric concentration of buried ice (pore-filling versus excess) provides information about the process that led to its deposition. We investigate the subsurface of Arcadia Planitia by measuring the depth of terraces in simple impact craters and mapping a widespread subsurface reflection in radar sounding data. Assuming that the contrast in material strengths responsible for the terracing is the same dielectric interface that causes the radar reflection, we can combine these data to estimate the dielectric constant of the overlying material.
    [Show full text]
  • Widespread Crater-Related Pitted Materials on Mars: Further Evidence for the Role of Target Volatiles During the Impact Process ⇑ Livio L
    Icarus 220 (2012) 348–368 Contents lists available at SciVerse ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Widespread crater-related pitted materials on Mars: Further evidence for the role of target volatiles during the impact process ⇑ Livio L. Tornabene a, , Gordon R. Osinski a, Alfred S. McEwen b, Joseph M. Boyce c, Veronica J. Bray b, Christy M. Caudill b, John A. Grant d, Christopher W. Hamilton e, Sarah Mattson b, Peter J. Mouginis-Mark c a University of Western Ontario, Centre for Planetary Science and Exploration, Earth Sciences, London, ON, Canada N6A 5B7 b University of Arizona, Lunar and Planetary Lab, Tucson, AZ 85721-0092, USA c University of Hawai’i, Hawai’i Institute of Geophysics and Planetology, Ma¯noa, HI 96822, USA d Smithsonian Institution, Center for Earth and Planetary Studies, Washington, DC 20013-7012, USA e NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA article info abstract Article history: Recently acquired high-resolution images of martian impact craters provide further evidence for the Received 28 August 2011 interaction between subsurface volatiles and the impact cratering process. A densely pitted crater-related Revised 29 April 2012 unit has been identified in images of 204 craters from the Mars Reconnaissance Orbiter. This sample of Accepted 9 May 2012 craters are nearly equally distributed between the two hemispheres, spanning from 53°Sto62°N latitude. Available online 24 May 2012 They range in diameter from 1 to 150 km, and are found at elevations between À5.5 to +5.2 km relative to the martian datum. The pits are polygonal to quasi-circular depressions that often occur in dense clus- Keywords: ters and range in size from 10 m to as large as 3 km.
    [Show full text]
  • Crater Geometry and Ejecta Thickness of the Martian Impact Crater Tooting
    Meteoritics & Planetary Science 42, Nr 9, 1615–1625 (2007) Abstract available online at http://meteoritics.org Crater geometry and ejecta thickness of the Martian impact crater Tooting Peter J. MOUGINIS-MARK and Harold GARBEIL Hawai‘i Institute of Geophysics and Planetology, University of Hawai‘i, Honolulu, Hawai‘i 96822, USA (Received 25 October 2006; revision accepted 04 March 2007) Abstract–We use Mars Orbiter Laser Altimeter (MOLA) topographic data and Thermal Emission Imaging System (THEMIS) visible (VIS) images to study the cavity and the ejecta blanket of a very fresh Martian impact crater ~29 km in diameter, with the provisional International Astronomical Union (IAU) name Tooting crater. This crater is very young, as demonstrated by the large depth/ diameter ratio (0.065), impact melt preserved on the walls and floor, an extensive secondary crater field, and only 13 superposed impact craters (all 54 to 234 meters in diameter) on the ~8120 km2 ejecta blanket. Because the pre-impact terrain was essentially flat, we can measure the volume of the crater cavity and ejecta deposits. Tooting crater has a rim height that has >500 m variation around the rim crest and a very large central peak (1052 m high and >9 km wide). Crater cavity volume (i.e., volume below the pre-impact terrain) is ~380 km3 and the volume of materials above the pre-impact terrain is ~425 km3. The ejecta thickness is often very thin (<20 m) throughout much of the ejecta blanket. There is a pronounced asymmetry in the ejecta blanket, suggestive of an oblique impact, which has resulted in up to ~100 m of additional ejecta thickness being deposited down-range compared to the up-range value at the same radial distance from the rim crest.
    [Show full text]
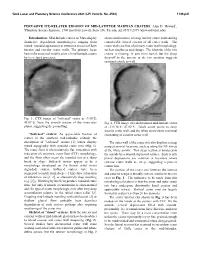
  • Pervasive Ice-Related Erosion of Mid-Latitude Martian Craters
    52nd Lunar and Planetary Science Conference 2021 (LPI Contrib. No. 2548) 1149.pdf PERVASIVE ICE-RELATED EROSION OF MID-LATITUDE MARTIAN CRATERS. Alan D. Howard1, 1Planetary Science Institute, 1700 East Fort Lowell, Suite 106, Tucson, AZ 85719-2395 ([email protected]). Introduction: Mid-latitude craters on Mars display shows maintenance of steep interior crater walls during distinctive degradation morphologies, ranging from considerable lateral erosion of all crater walls. The muted, rounded appearance to extensive erosion of both crater walls are free of primary crater wall morphology, interior and exterior crater walls. The primary focus such as roughness and slumps. The joint rim of the two here is the erosional modification of mid-latitude craters craters is missing, in part from burial, but the sharp by ice-related processes. drop-off to the interior at the rim junction suggests erosional attack as well. Fig. 1. CTX image of "softened" crater at -9.10°E, 45.83°S. Note the smooth texture of the intercrater Fig. 2. CTX image of a skeletonized mid-latitude crater plains, suggesting deep mantling. at -130.38°E, 47.02°S. Black arrow points to steep interior crater wall, and the white arrow show erosional "Softened" craters: An appreciable fraction of steepening of exterior crater wall. craters in the southern mid-latitudes embody the description of "softened" craters [1] which display The outer wall of the crater rim also displays a steep muted topography with rounded crater rims (Fig. 1). scarp at several locations, such as along the NE rim as The crater floor is often relatively flat, sometimes with at the white arrows.
    [Show full text]