Statistical Problem Posing, Problem Refining, and Further Reflection in Grade 6
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Sports Council Wales Annual Report 2004-05
Developing Sport & Physical Activity in Wales The Sports Council for Wales is the national organisation responsible for developing and promoting sport and active lifestyles. It is the main adviser on sporting matters to the Welsh Assembly Government and is responsible for distributing funds from the National Lottery to sport in Wales. The Council aims to be one of the main Subsequently, the Council’s main focus is to contributors to ‘Climbing Higher’, the Welsh increase the frequency of participation by Assembly Government’s strategy for sport persuading those who are currently and physical activity. It fully subscribes to sedentary to become more active and to the Assembly’s vision for a physically active encourage people, young and old, to and sporting nation, namely: develop a portfolio of activities through which to achieve healthy levels of activity. • Wales needs to be more physically active The themes of the Council’s work are: in order to be a healthier nation; • Active young people; • Wales needs healthy citizens to deliver long term prosperity; • Active communities; • Wales needs to maximise the synergy • Developing people; between sport, active recreation and the • Developing places; natural environment; • Developing performance and excellence. • Wales needs people to be more physically literate; In addition, the Council has committed to a shift from grants management to positioning • Wales needs more physically active itself as a development agency by becoming communities; an effective advocate for sport and physical • Wales needs systematic and sustainable activity, the marketing of healthy lifestyles success in the sports that matter most and intervention directed at the best use of to us. -

Welsh Athletics Milestones
Welsh Athletics Milestones Recalled by Clive Williams 1860 John Chambers holds a sports meeting at Hafod House, Aberystwyth - probably the first record of an athletics meeting being held in Wales 1865 Chambers organises “athletic sports” at Aberystwyth. 1865 William Richards, born in “Glamorgan” sets a world record for the mile with 4 mins. 17 ¼ seconds. 1871 St. David’s College Lampeter and Llandovery College hold athletics “sports” meetings. 1875 Newport Athletic Club formed and holds “athletic sports.” 1877 Cardiff-born William Gale achieves the phenomenal deed of walking 1,500 miles in 1,000 hours. He was the world’s leading pedestrian. 1879 Llanfair Caereinion Powys-born George Dunning sets a world 40 miles record at Stamford Bridge of 4:50.12. 1880 Newport AC represented by Richard Mullock at the formation of the AAA at The Randolph Hotel, Oxford - Chambers also there. 1881 Dunning effectively sets an inaugural world record for the half-marathon when he runs 1:13.46 on a track at Stamford Bridge. The distance is actually 13 miles 440 yards, i.e. further than the designated half marathon distance of 13 miles 192.5 yards. 1881 Dunning becomes the first Welsh born athlete to win the (English) National cross country title. 1882 Roath (Cardiff) Harriers formed. They amalgamated with Birchgrove (Cardiff) Harriers in 1968 to form Cardiff AAC.1890. 1890 Will Parry, born in Buttington, near Welshpool wins the (English) National cross country title for a third successive year. 1893 First Welsh amateur track championships held as part of an open sports meeting. Just 2 events held - 100 yards and mile won by Charles Thomas (Reading AC) and Hugh Fairlamb (Roath). -
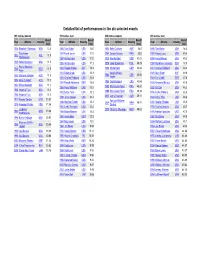
Detailed List of Performances in the Six Selected Events
Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976 -

The 1994 Lliswerry 8 Mile Road Race
The 1994 Lliswerry 8 Mile Road Race Senior Men Senior Women 1 Tony Graham 39.54 Newport Harriers 1 Lynch 47.44 Newport Harriers 2 Paul Richards 40.30 Swansea Harriers 2 Beccy Cameron 49.44 Bridgend A C 3 Phil Cook 40.47 Barry and Vale 3 Alison Scivens 51.16 Griffithstown Harriers 4 Mark Healy 41.00 Newport Harriers 4 Angharad Mair 52.45 Les Croupiers 5 Danny Norton 42.88 Rhondda Valley Runners 5 M Blue 53.26 Bitton Ferry R R 6 David Povall 42.48 Newport Harriers 6 Clare Knox 53.57 Cardiff Triathletes 7 Mark Dowden 42.58 Clevedon A C 7 Sharon Woods 54.53 Griffithstown Harriers 8 Chris Slowley 43.18 Bristol A C 8 Amanda Vowles 55.30 Chepstow Harriers 9 Mark Mussa 44.06 Heartbeat Wales 9 Gaynor Ambler 56.01 San Domenico 10 Ieuan Jones 44.08 Cardiff Triathletes 10 Judith Llewellyn 60.45 U/A Male Vet 40 Women Vet 35 1 John Davies 44.10 Pegasus R C 1 Joanna Thompson 44.11 City of Bath A C 2 R Morris 45.12 San Domenico 2 Trudi Thomson 46.37 B.T. Pitreavie 3 Mike Chandler 45.16 Caerphilly R C 3 Melanie Carter 56.21 Penarth & Dinas Runners 4 David Weston 46.05 Newport Harriers 4 Margaret Rabaiotti 57.35 Penarth & Dinas Runners 5 John Crutcher 46.25 Bridgend A C 5 Kathryn McDermot 60.47 U/A 6 Ian Kirkpatrick 46.31 Sospan R R 6 B Watts 61.30 Gwent Police 7 Kevin Fulthorpe 47.27 Cardiff A C 7 Helen Davies 62.52 U/A 8 Martin Lawrence 48.06 Hengoed R R 8 Jacqueline Wilding 66.23 Brecon Bounders 9 Dave Walsh 48.35 Les Croupiers 9 Dawn Teague 70.40 Forest of Dean 10 Phillip Miles 49.21 Club 69 10 Janice Clement 71.18 Penarth & Dinas Runners Male Vet -

AAA Club Newsletter No. 18, November 1966
LYNN DAVIES (Roatli (Cardiff) Harriers) ISSUE No. IS NOVEMBER, 1966 Olympic record holder ‘Ovaltine’ is the only food drink which What makes ‘Ovaltine’ the cho has been officially recognized for serv sen drink of champions ? Only ing to competitors at every Olympic ‘Ovaltine’ gives you all the good Games since 1932—and at every ness of barley malt, milk, eggs British Empire Games since they and added vitamins. No other began. During the 1964 Olympics over drink can match the way ‘Ovaltine’ 500,000 cups of ‘Ovaltine’ were served helps to build up energy, strength to athletes and officials—more than at artdstamina. So joi n the champions any other Olympic Games. in a regular cup of ‘Ovaltine’. OVALTINE the drink of champions Photographs were supplied by Mark Shearman, 23, Lynwood Drive, Worcester Park, Surrey. JIM HOGAN (Polytechnic Harriers) “ My Sometime Friend ” NORMAN HARRIS HERE is a story in the Bible of an army of Gideon, an army reduced from T 30,000 to a mere 500 by sending back all those whose heart was not fully in the battle and those who showed imprudence in a special test. The 500 who remained remind me of marathon runners. It makes me think of getting together an army of runners, of turning away all those who are not really keen on the idea of running 26 miles, of then offering a guarantee of success in any other event. There would not be many left—but there would be some. It is an argument by those who are not fully in sympathy with the decathlon that this competition attracts only those who cannot be the best in any one single event. -

BRONZO 2016 Usain Bolt
OLIMPIADI L'Albo d'Oro delle Olimpiadi Atletica Leggera UOMINI 100 METRI ANNO ORO - ARGENTO - BRONZO 2016 Usain Bolt (JAM), Justin Gatlin (USA), Andre De Grasse (CAN) 2012 Usain Bolt (JAM), Yohan Blake (JAM), Justin Gatlin (USA) 2008 Usain Bolt (JAM), Richard Thompson (TRI), Walter Dix (USA) 2004 Justin Gatlin (USA), Francis Obikwelu (POR), Maurice Greene (USA) 2000 Maurice Greene (USA), Ato Boldon (TRI), Obadele Thompson (BAR) 1996 Donovan Bailey (CAN), Frank Fredericks (NAM), Ato Boldon (TRI) 1992 Linford Christie (GBR), Frank Fredericks (NAM), Dennis Mitchell (USA) 1988 Carl Lewis (USA), Linford Christie (GBR), Calvin Smith (USA) 1984 Carl Lewis (USA), Sam Graddy (USA), Ben Johnson (CAN) 1980 Allan Wells (GBR), Silvio Leonard (CUB), Petar Petrov (BUL) 1976 Hasely Crawford (TRI), Don Quarrie (JAM), Valery Borzov (URS) 1972 Valery Borzov (URS), Robert Taylor (USA), Lennox Miller (JAM) 1968 James Hines (USA), Lennox Miller (JAM), Charles Greene (USA) 1964 Bob Hayes (USA), Enrique Figuerola (CUB), Harry Jeromé (CAN) 1960 Armin Hary (GER), Dave Sime (USA), Peter Radford (GBR) 1956 Bobby-Joe Morrow (USA), Thane Baker (USA), Hector Hogan (AUS) 1952 Lindy Remigino (USA), Herb McKenley (JAM), Emmanuel McDonald Bailey (GBR) 1948 Harrison Dillard (USA), Norwood Ewell (USA), Lloyd LaBeach (PAN) 1936 Jesse Owens (USA), Ralph Metcalfe (USA), Martinus Osendarp (OLA) 1932 Eddie Tolan (USA), Ralph Metcalfe (USA), Arthur Jonath (GER) 1928 Percy Williams (CAN), Jack London (GBR), Georg Lammers (GER) 1924 Harold Abrahams (GBR), Jackson Scholz (USA), Arthur -

ENGLISH ARTWORK Copy
ANNUAL REPORT AND ACCOUNTS 2005/06 Sports Council for Wales Annual Report and Accounts 2005/06 01 Members 2005/06 Contents Chair 02 Chair’s Statement Mr Philip Carling 04 ‘Climbing Higher’ 08 Health Vice-Chair 10 Active Young People Miss Anne Ellis OBE 18 Economy and Culture Members 29 Mainstreaming the Welsh Language Mrs Christine Gittoes 30 Society and Environment _ Mr Clive Thomas 32 Wales Land of Natural Beauty Mr Huw Thomas 35 Targeting the Hard to Reach Ms Sue Williams 38 Success on a World Stage Ms Nicola Bolton 45 Gifted Coaches Mr Bob Lowe 49 Domestic Structures and Facilities Mr David Davies 53 The National Centres Mr Lynn Davies CBE 56 Commonwealth Games Melbourne 2006 Councillor Keith Evans 58 Serving our Customers 59 The Sports Council for Wales and The Sports Co-opted Member Council for Wales Trust Mr D. Robert Turner 61 The Statement of the Auditor General for Directors Wales to the Sports Council for Wales Chief Executive 62 Summary Consolidated Income and Dr Huw Jones Expenditure Account for the Year ended 31 March 2006 Director of Excellence Mr Graham Davies 63 Summary Consolidated Balance Sheet as at 31 March 2006 Director of Sports Participation & Physical Activity 64 Summary Consolidated Cashflow Statement (until 1/11/2005 then seconded to Welsh for the Year ended 31 March 2006 Assembly Government) 65 Sports Council for Wales - Lottery Distribution Mrs Sara Butlin Account Acting Director of Sports Participation & Physical 68 Statement of the Comptroller and Auditor Activity (from 1/2/2006) General to the Houses of -

Welsh Athletics Milestones
Welsh Athletics Milestones Recalled by Clive Williams 1860 John Chambers holds a sports meeting at Hafod House, Aberystwyth - probably the first record of an athletics meeting being held in Wales 1865 Chambers organises “athletic sports” at Aberystwyth. 1865 William Richards, born in “Glamorgan” sets a world record for the mile with 4 mins. 17 ¼ seconds. 1871 St. David’s College Lampeter and Llandovery College hold athletics “sports” meetings. 1875 Newport Athletic Club formed and holds “athletic sports.” 1877 Cardiff-born William Gale achieves the phenomenal deed of walking 1,500 miles in 1,000 hours. He was the world’s leading pedestrian. 1879 Llanfair Caereinion Powys-born George Dunning sets a world 40 miles record at Stamford Bridge of 4:50.12. 1880 Newport AC represented by Richard Mullock at the formation of the AAA at The Randolph Hotel, Oxford - Chambers also there. 1881 Dunning effectively sets an inaugural world record for the half-marathon when he runs 1:13.46 on a track at Stamford Bridge. The distance is actually 13 miles 440 yards, i.e. further than the designated half marathon distance of 13 miles 192.5 yards. 1881 Dunning becomes the first Welsh born athlete to win the (English) National cross country title. 1882 Roath (Cardiff) Harriers formed. They amalgamated with Birchgrove (Cardiff) Harriers in 1968 to form Cardiff AAC.1890. 1890 Will Parry, born in Buttington, near Welshpool wins the (English) National cross country title for a third successive year. 1890: St. Asaph-born Norman David Morgan wins the AAA 100 yards title during his residence in Ireland. -

Long Jump: Men Maths Worksheets from Mathsblog.Co.Uk
Long Jump: men Maths worksheets from mathsblog.co.uk Here are some of the most famous long jump winners. Year City Name Country Distance 1896 Athens Ellery Clark USA 6.35 m 1908 London Frank Irons USA 7.48 m 1936 Berlin Jesse Owens USA 8.06 m 1964 Tokyo Lynn Davies GB 8.07 m 1968 Mexico City Bob Beamon USA 8.90 m 1988 Seoul Carl Lewis USA 8.72 m 2004 Athens Dwight Phillips USA 8.59 m 1. The USA like winning the long jump. Who is the only non-USA athlete on this table of long jump winners? ........................................................................................................................................ 2. How much further did Jesse Owens jump than Ellery Clark? ............................................................. 3. How much shorter was Lynn Davies’s best jump than Carl Lewis’s? ................................................ 4. How many centimetres short of Bob Beamon’s jump was Dwight Phillips?......................................... 5. How much shorter was Frank Iron’s best jump than Carl Lewis’s? ................................................ 6. Bob Beamon held the Long Jump record from 1968, until Mike Powell jumped 8.95m in 1991. Do you think anyone will ever jump more than 9 metres............................................................................ 7. Why do you think this?...................................................................................................................... ................................................................................................................................................................ Page 1 Long Jump: men Maths worksheets from mathsblog.co.uk Draw a graph to show the distances jumped by these 7 athletes. Distance jumped in metres 1m 2m 3m 4m 5m 6m 7m 8m 9m Ellery Clark Frank Irons Jesse Owens Lynn Davies Bob Beamon Athletes Carl Lewis Dwight Phillips This year’s longest jump Me The World Long Jump record was held by Bob Beamon since 1968 when he jumped 8.90m. -

Team GB at Tokyo 2020
TOKYO 2020 OLYMPIC GAMES JULY 23 - AUGUST 08 TABLE OF Contents Team GB at Tokyo 2020 002 003 004 006 FOREWORD TEAM GB MEDIA WELCOME TO COMPETITION CONTACTS TOKYO SCHEDULE 008 010 012 TEAM GB AT HISTORICAL TEAM GB TOKYO 2020 MEDAL TALLY SPORT-BY-SPORT 3 MEDIA GUIDE FOREWORD TEAM GB MEDIA CONTACTS at an ‘away’ Games – and the media operations Director of Communications: Scott Field, Aquatics: Artistic Swimming, Marathon Judo: Katriona Bush, Katriona.Bush@ overlay in Tokyo. Please use all the links available in [email protected], & Diving Individual: David Gerty, TeamGB.com, +81 (0) 7014104115 this guide to click through to our athlete profiles or to +81 (0) 7014103668 [email protected], Modern Pentathlon: Craig Davies, follow their progress on social media +81 (0) 7014103709 Chief Press Attaché: Thomas Rowland, [email protected], +81 (0) [email protected], Athletics: Liz Birchall, 7014104053 You will find a variety of information to help you +81 (0) 7014104392 [email protected], navigate the 17 days of competition at Tokyo 2020 +81 (0) 7014104172 Rowing: Shelley Wyatt, Shelley.Wyatt@ as well as useful contacts for your time in Japan. The Deputy Chief Press Attaché and Head TeamGB.com, +81 (0) 7014104360 entire Team GB-appointed media team are here of Managing Victory: Laura Craig, Laura. Badminton: Gemma Field, [email protected], +81 (0) 7014104145 [email protected], Rugby Sevens: Charlotte Harwood, to help you, so please do be in contact during the +81 (0) 7014104053 [email protected], +81 Games if there is anything we can be of assistance Preparation Camp Media Manager: (0) 7014103957 with. -

Quick Reads a Toolkit for Union Learning Reps Wales TUC Cymru
Quick Reads A toolkit for Union Learning Reps Wales TUC Cymru 1 About the Quick Reads toolkit for Union Learning Reps The aim of this guide is to help union learning reps home and abroad. (ULRs) in Wales to use Quick Reads books in an effective way to promote reading for pleasure in the workplace. The Quick Reads project in Wales is coordinated Quick Reads books are short, sharp shots of by the Welsh Books Council and supported by the entertainment. They are books for people who Welsh Government. want a fun, fast read, and ideal for those who have lost the reading habit or find reading tough. Each year four new titles are published. With one in Improved reading habits can lead to other benefits six adults still struggling to read, the Quick Reads and as a ULR, you can use these books as a way campaign aims to break down barriers and get of introducing yourself to your existing members Wales reading by producing short, gripping books and new potential members. It could also be a available from libraries, bookshops and online for pro-active way to explain just £1. your role as a ULR and begin discussing Angharad Sinclair, from the Welsh Books Council, learning opportunities with said: colleagues that you may not have had previous ‘Quick Reads are short, snappy books with fewer contact. than 100 pages each, and are especially written for people who wish to improve their skills and This guide has confidence around reading. By taking a bite-sized been developed in approach to reading we aim to overcome any partnership by the confidence issues and show that reading can be a Welsh Books Council fun and inspiring activity for all.’ and the Wales TUC after consultation with ULR’s across Wales who either already use or wish to use Quick Reads as a supporting tool to their work as well as a recruitment tool to attract new members through reading activities. -
Division I Men's Outdoor Track Championships Records Book
DIVISION I MEN’S OUTDOOR TRACK CHAMPIONSHIPS RECORDS BOOK 2019 Championship 2 History 9 All-Time Team Results 37 2019 CHAMPIONSHIP Place School Pts. Place School Pts. 2019 TEAM RESULTS Virginia 16 Minnesota 5 Wisconsin 16 Saint Francis (PA) 5 Place School Pts. 22. Arizona 14 Utah St. 5 1. Texas Tech 60 Baylor 14 45. Southern Utah 4½ 2. Florida 50 24. North Dakota St. 13 46. Arizona St. 4 3. Houston 40 Southern Miss 13 Arkansas St. 4 4. Georgia 32½ 26. Kansas St. 12 Coppin St. 4 5. Stanford 32 Michigan 12 Wichita St. 4 6. Texas A&M 29 28. Iowa St. 10 50. Air Force 3 7. LSU 28 Kennesaw St. 10 Alabama St. 3 8. BYU 27 Notre Dame 10 Harvard 3 9. Texas 26 South Dakota 10 Northern Ariz. 3 10. Alabama 25 TCU 10 Washington 3 11. Mississippi St. 24 33. Indiana 9 55. Houston Baptist 2 12. Oregon 23 34. Kentucky 8 Illinois 2 South Carolina 23 Michigan St. 8 Long Beach St. 2 14. Kansas 21 36. Purdue 7 Penn St. 2 15. Arkansas 19 37. Middle Tenn. 6 61. Akron 1 N.C. A&T 19 Sam Houston St. 6 California 1 17. Florida St. 18 Southern California 6 Tennessee 1 18. Oklahoma St. 16 40. Iowa 5 Villanova 1 UCLA 16 Liberty 5 2019 INDIVIDUAL RESULTS Name School Time Wind 19. Travis Collins Houston 10.24 (10.231) 2.6 100-Meter Dash Final 20. Roy Ejiakuekwu Arkansas 10.24 (10.239) 1.3 21. Jace Comick Texas A&M 10.30 1.3 Name School Time Wind 22.