Data Structures Heap
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tree-Combined Trie: a Compressed Data Structure for Fast IP Address Lookup
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 12, 2015 Tree-Combined Trie: A Compressed Data Structure for Fast IP Address Lookup Muhammad Tahir Shakil Ahmed Department of Computer Engineering, Department of Computer Engineering, Sir Syed University of Engineering and Technology, Sir Syed University of Engineering and Technology, Karachi Karachi Abstract—For meeting the requirements of the high-speed impact their forwarding capacity. In order to resolve two main Internet and satisfying the Internet users, building fast routers issues there are two possible solutions one is IPv6 IP with high-speed IP address lookup engine is inevitable. addressing scheme and second is Classless Inter-domain Regarding the unpredictable variations occurred in the Routing or CIDR. forwarding information during the time and space, the IP lookup algorithm should be able to customize itself with temporal and Finding a high-speed, memory-efficient and scalable IP spatial conditions. This paper proposes a new dynamic data address lookup method has been a great challenge especially structure for fast IP address lookup. This novel data structure is in the last decade (i.e. after introducing Classless Inter- a dynamic mixture of trees and tries which is called Tree- Domain Routing, CIDR, in 1994). In this paper, we will Combined Trie or simply TC-Trie. Binary sorted trees are more discuss only CIDR. In addition to these desirable features, advantageous than tries for representing a sparse population reconfigurability is also of great importance; true because while multibit tries have better performance than trees when a different points of this huge heterogeneous structure of population is dense. -

Game Trees, Quad Trees and Heaps
CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself. -
Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
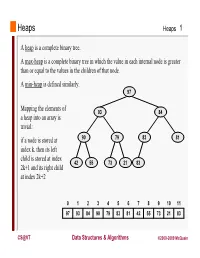
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

L11: Quadtrees CSE373, Winter 2020
L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373, -

Binary Search Tree
ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is -

6.172 Lecture 19 : Cache-Oblivious B-Tree (Tokudb)
How TokuDB Fractal TreeTM Indexes Work Bradley C. Kuszmaul Guest Lecture in MIT 6.172 Performance Engineering, 18 November 2010. 6.172 —How Fractal Trees Work 1 My Background • I’m an MIT alum: MIT Degrees = 2 × S.B + S.M. + Ph.D. • I was a principal architect of the Connection Machine CM-5 super computer at Thinking Machines. • I was Assistant Professor at Yale. • I was Akamai working on network mapping and billing. • I am research faculty in the SuperTech group, working with Charles. 6.172 —How Fractal Trees Work 2 Tokutek A few years ago I started collaborating with Michael Bender and Martin Farach-Colton on how to store data on disk to achieve high performance. We started Tokutek to commercialize the research. 6.172 —How Fractal Trees Work 3 I/O is a Big Bottleneck Sensor Query Systems include Sensor Disk Query sensors and Sensor storage, and Query want to perform Millions of data elements arrive queries on per second Query recently arrived data using indexes. recent data. Sensor 6.172 —How Fractal Trees Work 4 The Data Indexing Problem • Data arrives in one order (say, sorted by the time of the observation). • Data is queried in another order (say, by URL or location). Sensor Query Sensor Disk Query Sensor Query Millions of data elements arrive per second Query recently arrived data using indexes. Sensor 6.172 —How Fractal Trees Work 5 Why Not Simply Sort? • This is what data Data Sorted by Time warehouses do. • The problem is that you Sort must wait to sort the data before querying it: Data Sorted by URL typically an overnight delay. -

AVL Tree, Bayer Tree, Heap Summary of the Previous Lecture
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture • TREE is hierarchical (non linear) data structure • Binary trees • Definitions • Full tree, complete tree • Enumeration ( preorder, inorder, postorder ) • Binary search tree (BST) AVL tree The AVL tree (named for its inventors Adelson-Velskii and Landis published in their paper "An algorithm for the organization of information“ in 1962) should be viewed as a BST with the following additional property: - For every node, the heights of its left and right subtrees differ by at most 1. Difference of the subtrees height is named balanced factor. A node with balance factor 1, 0, or -1 is considered balanced. As long as the tree maintains this property, if the tree contains n nodes, then it has a depth of at most log2n. As a result, search for any node will cost log2n, and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost log2n, even in the worst case. AVL tree AVL tree Not AVL tree Realization of AVL tree element struct AVLnode { int data; AVLnode* left; AVLnode* right; int factor; // balance factor } Adding a new node Insert operation violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced. -
B-Trees M-Ary Search Tree Solution
M-ary Search Tree B-Trees • Maximum branching factor of M • Complete tree has height = Section 4.7 in Weiss # disk accesses for find : Runtime of find : 2 Solution: B-Trees B-Trees • specialized M-ary search trees What makes them disk-friendly? • Each node has (up to) M-1 keys: 1. Many keys stored in a node – subtree between two keys x and y contains leaves with values v such that • All brought to memory/cache in one access! 3 7 12 21 x ≤ v < y 2. Internal nodes contain only keys; • Pick branching factor M Only leaf nodes contain keys and actual data such that each node • The tree structure can be loaded into memory takes one full irrespective of data object size {page, block } x<3 3≤x<7 7≤x<12 12 ≤x<21 21 ≤x • Data actually resides in disk of memory 3 4 B-Tree: Example B-Tree Properties ‡ B-Tree with M = 4 (# pointers in internal node) and L = 4 (# data items in leaf) – Data is stored at the leaves – All leaves are at the same depth and contain between 10 40 L/2 and L data items – Internal nodes store up to M-1 keys 3 15 20 30 50 – Internal nodes have between M/2 and M children – Root (special case) has between 2 and M children (or root could be a leaf) 1 2 10 11 12 20 25 26 40 42 AB xG 3 5 6 9 15 17 30 32 33 36 50 60 70 Data objects, that I’ll Note: All leaves at the same depth! ignore in slides 5 ‡These are technically B +-Trees 6 1 Example, Again B-trees vs. -

AVL Trees and Rotations
/ AVL trees and rotations Q1 Operations (insert, delete, search) are O(height) Tree height is O(log n) if perfectly balanced ◦ But maintaining perfect balance is O(n) Height-balanced trees are still O(log n) ◦ For T with height h, N(T) ≤ Fib(h+3) – 1 ◦ So H < 1.44 log (N+2) – 1.328 * AVL (Adelson-Velskii and Landis) trees maintain height-balance using rotations Are rotations O(log n)? We’ll see… / or = or \ Different representations for / = \ : Just two bits in a low-level language Enum in a higher-level language / Assume tree is height-balanced before insertion Insert as usual for a BST Move up from the newly inserted node to the lowest “unbalanced” node (if any) ◦ Use the balance code to detect unbalance - how? Do an appropriate rotation to balance the sub-tree rooted at this unbalanced node For example, a single left rotation: Two basic cases ◦ “See saw” case: Too-tall sub-tree is on the outside So tip the see saw so it’s level ◦ “Suck in your gut” case: Too-tall sub-tree is in the middle Pull its root up a level Q2-3 Unbalanced node Middle sub-tree attaches to lower node of the “see saw” Diagrams are from Data Structures by E.M. Reingold and W.J. Hansen Q4-5 Unbalanced node Pulled up Split between the nodes pushed down Weiss calls this “right-left double rotation” Q6 Write the method: static BalancedBinaryNode singleRotateLeft ( BalancedBinaryNode parent, /* A */ BalancedBinaryNode child /* B */ ) { } Returns a reference to the new root of this subtree. -

Leftist Heap: Is a Binary Tree with the Normal Heap Ordering Property, but the Tree Is Not Balanced. in Fact It Attempts to Be Very Unbalanced!
Leftist heap: is a binary tree with the normal heap ordering property, but the tree is not balanced. In fact it attempts to be very unbalanced! Definition: the null path length npl(x) of node x is the length of the shortest path from x to a node without two children. The null path lengh of any node is 1 more than the minimum of the null path lengths of its children. (let npl(nil)=-1). Only the tree on the left is leftist. Null path lengths are shown in the nodes. Definition: the leftist heap property is that for every node x in the heap, the null path length of the left child is at least as large as that of the right child. This property biases the tree to get deep towards the left. It may generate very unbalanced trees, which facilitates merging! It also also means that the right path down a leftist heap is as short as any path in the heap. In fact, the right path in a leftist tree of N nodes contains at most lg(N+1) nodes. We perform all the work on this right path, which is guaranteed to be short. Merging on a leftist heap. (Notice that an insert can be considered as a merge of a one-node heap with a larger heap.) 1. (Magically and recursively) merge the heap with the larger root (6) with the right subheap (rooted at 8) of the heap with the smaller root, creating a leftist heap. Make this new heap the right child of the root (3) of h1. -

Tries and String Matching
Tries and String Matching Where We've Been ● Fundamental Data Structures ● Red/black trees, B-trees, RMQ, etc. ● Isometries ● Red/black trees ≡ 2-3-4 trees, binomial heaps ≡ binary numbers, etc. ● Amortized Analysis ● Aggregate, banker's, and potential methods. Where We're Going ● String Data Structures ● Data structures for storing and manipulating text. ● Randomized Data Structures ● Using randomness as a building block. ● Integer Data Structures ● Breaking the Ω(n log n) sorting barrier. ● Dynamic Connectivity ● Maintaining connectivity in an changing world. String Data Structures Text Processing ● String processing shows up everywhere: ● Computational biology: Manipulating DNA sequences. ● NLP: Storing and organizing huge text databases. ● Computer security: Building antivirus databases. ● Many problems have polynomial-time solutions. ● Goal: Design theoretically and practically efficient algorithms that outperform brute-force approaches. Outline for Today ● Tries ● A fundamental building block in string processing algorithms. ● Aho-Corasick String Matching ● A fast and elegant algorithm for searching large texts for known substrings. Tries Ordered Dictionaries ● Suppose we want to store a set of elements supporting the following operations: ● Insertion of new elements. ● Deletion of old elements. ● Membership queries. ● Successor queries. ● Predecessor queries. ● Min/max queries. ● Can use a standard red/black tree or splay tree to get (worst-case or expected) O(log n) implementations of each. A Catch ● Suppose we want to store a set of strings. ● Comparing two strings of lengths r and s takes time O(min{r, s}). ● Operations on a balanced BST or splay tree now take time O(M log n), where M is the length of the longest string in the tree. -

Binary Tree Fall 2017 Stony Brook University Instructor: Shebuti Rayana [email protected] Introduction to Tree
CSE 230 Intermediate Programming in C and C++ Binary Tree Fall 2017 Stony Brook University Instructor: Shebuti Rayana [email protected] Introduction to Tree ■ Tree is a non-linear data structure which is a collection of data (Node) organized in hierarchical structure. ■ In tree data structure, every individual element is called as Node. Node stores – the actual data of that particular element and – link to next element in hierarchical structure. Tree with 11 nodes and 10 edges Shebuti Rayana (CS, Stony Brook University) 2 Tree Terminology ■ Root ■ In a tree data structure, the first node is called as Root Node. Every tree must have root node. In any tree, there must be only one root node. Root node does not have any parent. (same as head in a LinkedList). Here, A is the Root node Shebuti Rayana (CS, Stony Brook University) 3 Tree Terminology ■ Edge ■ The connecting link between any two nodes is called an Edge. In a tree with 'N' number of nodes there will be a maximum of 'N-1' number of edges. Edge is the connecting link between the two nodes Shebuti Rayana (CS, Stony Brook University) 4 Tree Terminology ■ Parent ■ The node which is predecessor of any node is called as Parent Node. The node which has branch from it to any other node is called as parent node. Parent node can also be defined as "The node which has child / children". Here, A is Parent of B and C B is Parent of D, E and F C is the Parent of G and H Shebuti Rayana (CS, Stony Brook University) 5 Tree Terminology ■ Child ■ The node which is descendant of any node is called as CHILD Node.