Basic Guidelines for Tuning with the XPS Motion Controller
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Report of the First Coordinated Inspection
EURODAC Supervision Coordination Group Report of the first coordinated inspection Brussels, 17 July 2007 Secretariat of the Eurodac Supervision Coordination Group EDPS, Rue Wiertz, 60 B-1047 Brussels e-mail [email protected] 1 Table of content I. Introduction ...............................................................................................................3 II. Background..............................................................................................................4 1. What is Eurodac?............................................................................................................ 4 2. Supervision of Eurodac .................................................................................................. 5 3. Coordinated inspection: a timely action ....................................................................... 6 III. Issues for inspection and methodology..................................................................6 1. Issues ................................................................................................................................6 2. Method of inspection....................................................................................................... 7 IV. Findings and evaluation.........................................................................................8 1. Preliminary observations................................................................................................ 8 2. Special searches.............................................................................................................. -

Voice Year America's Oldest Weetly College Newspaper, Founded on November 13, 1C23, Celebrates Anniversary Prof Resigns; Russian Dept
The College of Wooster Open Works The oV ice: 1981-1990 "The oV ice" Student Newspaper Collection 11-18-1983 The oW oster Voice (Wooster, OH), 1983-11-18 Wooster Voice Editors Follow this and additional works at: https://openworks.wooster.edu/voice1981-1990 Recommended Citation Editors, Wooster Voice, "The oosW ter Voice (Wooster, OH), 1983-11-18" (1983). The Voice: 1981-1990. 72. https://openworks.wooster.edu/voice1981-1990/72 This Book is brought to you for free and open access by the "The oV ice" Student Newspaper Collection at Open Works, a service of The oC llege of Wooster Libraries. It has been accepted for inclusion in The oV ice: 1981-1990 by an authorized administrator of Open Works. For more information, please contact [email protected]. THE VOICE VOLUME C WOOSTER. OHIO. FRIDAY. NOVEUBER It. ItSS NUXXCZH 19 Voice Year America's Oldest Weetly College Newspaper, Founded On November 13, 1C23, Celebrates Anniversary Prof Resigns; Russian Dept. Questionable Ichabod's 41 m : : By ' . -- ... Emily Drags "fc-.-.."--- . ..-- j mimmH,BW ' wl i. nmyi .i !.' .. Last week. Professor Joel Wilkin- Campaign son. Chairman of the Russian Studies Department, announced his $2800 resignation effective December 31. Gets non-teachi- ng "He accepted a posi- . J anew ..tt-- t lilltZl'i .' Jtll Ml '. tion .at another association" com- mented Don Harvard, Vice Presi- " r-- L-- " I. v,Jt.-4-. ,l.IlilIWair.iSeS wiai)iw dent of Academic Affairs. This By Dob Sandfbrd occurrence has only furthered the Ichabod's was the site last week- debate that Is In progress as to the end of The College's first-ev- er 24 role Russian Studies should play in hour dance marathon. -

Roadside Safety Design and Devices International Workshop
TRANSPORTATION RESEARCH Number E-C172 February 2013 Roadside Safety Design and Devices International Workshop July 17, 2012 Milan, Italy TRANSPORTATION RESEARCH BOARD 2013 EXECUTIVE COMMITTEE OFFICERS Chair: Deborah H. Butler, Executive Vice President, Planning, and CIO, Norfolk Southern Corporation, Norfolk, Virginia Vice Chair: Kirk T. Steudle, Director, Michigan Department of Transportation, Lansing Division Chair for NRC Oversight: Susan Hanson, Distinguished University Professor Emerita, School of Geography, Clark University, Worcester, Massachusetts Executive Director: Robert E. Skinner, Jr., Transportation Research Board TRANSPORTATION RESEARCH BOARD 2012–2013 TECHNICAL ACTIVITIES COUNCIL Chair: Katherine F. Turnbull, Executive Associate Director, Texas A&M Transportation Institute, Texas A&M University System, College Station Technical Activities Director: Mark R. Norman, Transportation Research Board Paul Carlson, Research Engineer, Texas A&M Transportation Institute, Texas A&M University System, College Station, Operations and Maintenance Group Chair Thomas J. Kazmierowski, Manager, Materials Engineering and Research Office, Ontario Ministry of Transportation, Toronto, Canada, Design and Construction Group Chair Ronald R. Knipling, Principal, safetyforthelonghaul.com, Arlington, Virginia, System Users Group Chair Mark S. Kross, Consultant, Jefferson City, Missouri, Planning and Environment Group Chair Joung Ho Lee, Associate Director for Finance and Business Development, American Association of State Highway and Transportation -

AOS Lidar Object Detection Systems
OPERATING INSTRUCTIO NS AOS LiDAR Object Detection Systems Product described Product name: AOS LiDAR Document identification Title: AOS LiDAR Operating Instructions Part number: 8016800/18UD Status: 2020-09 Manufacturer SICK AG Erwin-Sick-Str. 1 · 79183 Waldkirch · Germany Trademarks IBM is a trademark of the International Business Machine Corporation. MS-DOS is a trademark of the Microsoft Corporation. Windows is a trademark of the Microsoft Corporation. Other product names in this document may also be trademarks and are only used here for identification purposes. Original documents The German version 8016731/18UD of this document is an original SICK AG document. SICK AG does not assume liability for the correctness of a non-authorized translation. In case of doubt, contact SICK AG or your local agency. Legal notes Subject to change without notice © SICK AG. All rights reserved 2 OPERATING INSTRUCTIO NS | AOS LiDAR 8016800/18UD/2020-09|SICK Subject to change without notice CONTENTS Contents 1 About these operating instructions ....................................................................... 6 1.1 Described software versions....................................................................... 6 1.2 Purpose of this document ........................................................................... 6 1.3 Target group .................................................................................................. 6 1.4 Information depth......................................................................................... 7 -

Jamming As a Curriculum of Resistance: Popular Music, Shared Intuitive Headspaces, and Rocking in the "Free" World
Georgia Southern University Digital Commons@Georgia Southern Electronic Theses and Dissertations Graduate Studies, Jack N. Averitt College of Spring 2015 Jamming as a Curriculum of Resistance: Popular Music, Shared Intuitive Headspaces, and Rocking in the "Free" World Mike Czech Follow this and additional works at: https://digitalcommons.georgiasouthern.edu/etd Part of the Art Education Commons, and the Curriculum and Instruction Commons Recommended Citation Czech, Mike, "Jamming as a Curriculum of Resistance: Popular Music, Shared Intuitive Headspaces, and Rocking in the "Free" World" (2015). Electronic Theses and Dissertations. 1270. https://digitalcommons.georgiasouthern.edu/etd/1270 This dissertation (open access) is brought to you for free and open access by the Graduate Studies, Jack N. Averitt College of at Digital Commons@Georgia Southern. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of Digital Commons@Georgia Southern. For more information, please contact [email protected]. JAMMING AS A CURRICULUM OF RESISTANCE: POPULAR MUSIC, SHARED INTUITIVE HEADSPACES, AND ROCKING IN THE “FREE” WORLD by MICHAEL R. CZECH (Under the Direction of John Weaver) ABSTRACT This project opens space for looking at the world in a musical way where “jamming” with music through playing and listening to it helps one resist a more standardized and dualistic way of seeing the world. Instead of having a traditional dissertation, this project is organized like a record album where each chapter is a Track that contains an original song that parallels and plays off the subject matter being discussed to make a more encompassing, multidimensional, holistic, improvisational, and critical statement as the songs and riffs move along together to tell why an arts-based musical way of being can be a choice and alternative in our lives. -

Design of a Simplified Test Track for Automated Transit Network Development
DESIGN OF A SIMPLIFIED TEST TRACK FOR AUTOMATED TRANSIT NETWORK DEVELOPMENT A Thesis Presented to The Faculty of the Department of Mechanical Engineering San José State University In Partial Fulfillment of the Requirements for the Degree Master of Science by Adam L. Krueger May 2014 © 2014 Adam L. Krueger ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled DESIGN OF A SIMPLIFIED TEST TRACK FOR AUTOMATED TRANSIT NETWORK DEVELOPMENT by Adam L. Krueger APPROVED FOR THE DEPARTMENT OF MECHANICAL ENGINEERING SAN JOSÉ STATE UNIVERSITY May 2014 Dr. Burford Furman Department of Mechanical Engineering Dr. Neyram Hemati Department of Mechanical Engineering Dr. Ping Hsu Department of Electrical Engineering ABSTRACT DESIGN OF A SIMPLIFIED TEST TRACK FOR AUTOMATED TRANSIT NETWORK DEVELOPMENT by Adam L. Krueger A scaled test platform has been developed for the purpose of testing, validating, and demonstrating key concepts of Automated Transit Networks (ATN). The test platform is relatively low cost, easily expandable, and it will allow future research and development to be done on control systems for ATN. The test platform and reference vehicle were designed to adhere to a requirements document that was constructed to specify the necessary features of a fully functioning design. The work described in this thesis adheres to the phase one implementation of the requirements document. The vehicle and track were designed using commercially available computer aided design software. The prototype track was then assembled, and the vehicles were manufactured using a finite deposition three-dimensional printer. A control system was designed to control the velocity and position of the vehicle. -

Artificial Intelligence and Civil Liability
STUDY Requested.z by the JURI committee Artificial Intelligence and Civil Liability Legal Affairs Policy Department for Citizens' Rights and Constitutional Affairs Directorate-General for Internal Policies PE 621.926 - July 2020 EN Artificial Intelligence and Civil Liability Legal Affairs Abstract This study – commissioned by the Policy Department C at the request of the Committee on Legal Affairs – analyses the notion of AI-technologies and the applicable legal framework for civil liability. It demonstrates how technology regulation should be technology- specific, and presents a Risk Management Approach, where the party who is best capable of controlling and managing a technology-related risk is held strictly liable, as a single entry point for litigation. It then applies such approach to four case-studies, to elaborate recommendations. This document was requested by the European Parliament's Committee on Legal Affairs. AUTHORS Andrea BERTOLINI, Ph.D., LL.M. (Yale) Assistant Professor of Private Law, Scuola Superiore Sant’Anna (Pisa) Director of the Jean Monnet - European Centre of Excellence on the Regulation of Robotics and AI (EURA) www.eura.santannapisa.it [email protected] ADMINISTRATOR RESPONSIBLE Giorgio MUSSA EDITORIAL ASSISTANT Sandrina MARCUZZO LINGUISTIC VERSIONS Original: EN ABOUT THE EDITOR Policy departments provide in-house and external expertise to support EP committees and other parliamentary bodies in shaping legislation and exercising democratic scrutiny over EU internal policies. To contact the Policy -
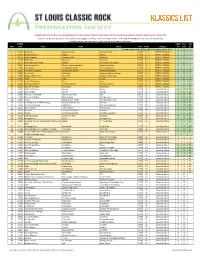
KLASSICS LIST Criteria
KLASSICS LIST criteria: 8 or more points (two per fan list, two for U-Man A-Z list, two to five for Top 95, depending on quartile); 1984 or prior release date Sources: ten fan lists (online and otherwise; see last page for details) + 2011-12 U-Man A-Z list + 2014 Top 95 KSHE Klassics (as voted on by listeners) sorted by points, Fan Lists count, Top 95 ranking, artist name, track name SLCRPS UMan Fan Top ID # ID # Track Artist Album Year Points Category A-Z Lists 95 35 songs appeared on all lists, these have green count info >> X 10 n 1 12404 Blue Mist Mama's Pride Mama's Pride 1975 27 PERFECT KLASSIC X 10 1 2 12299 Dead And Gone Gypsy Gypsy 1970 27 PERFECT KLASSIC X 10 2 3 11672 Two Hangmen Mason Proffit Wanted 1969 27 PERFECT KLASSIC X 10 5 4 11578 Movin' On Missouri Missouri 1977 27 PERFECT KLASSIC X 10 6 5 11717 Remember the Future Nektar Remember the Future 1973 27 PERFECT KLASSIC X 10 7 6 10024 Lake Shore Drive Aliotta Haynes Jeremiah Lake Shore Drive 1971 27 PERFECT KLASSIC X 10 9 7 11654 Last Illusion J.F. Murphy & Salt The Last Illusion 1973 27 PERFECT KLASSIC X 10 12 8 13195 The Martian Boogie Brownsville Station Brownsville Station 1977 27 PERFECT KLASSIC X 10 13 9 13202 Fly At Night Chilliwack Dreams, Dreams, Dreams 1977 27 PERFECT KLASSIC X 10 14 10 11696 Mama Let Him Play Doucette Mama Let Him Play 1978 27 PERFECT KLASSIC X 10 15 11 11547 Tower Angel Angel 1975 27 PERFECT KLASSIC X 10 19 12 11730 From A Dry Camel Dust Dust 1971 27 PERFECT KLASSIC X 10 20 13 12131 Rosewood Bitters Michael Stanley Michael Stanley 1972 27 PERFECT -

Peter Schilling 120 Grad Mp3, Flac, Wma
Peter Schilling 120 Grad mp3, flac, wma DOWNLOAD LINKS (Clickable) Genre: Electronic / Pop Album: 120 Grad Country: Europe Released: 1984 Style: Synth-pop MP3 version RAR size: 1309 mb FLAC version RAR size: 1253 mb WMA version RAR size: 1825 mb Rating: 4.8 Votes: 934 Other Formats: ASF WAV ADX TTA AA AC3 MP1 Tracklist Hide Credits Hitze Der Nacht A1 Bass – Tissy ThiersWritten By – Armin Sabol/P. SchillingWritten-By – Armin Sabol, P. 5:16 Schilling* Hurricane A2 4:30 Written-By – P. Schilling* Region 804 A3 4:18 Keyboards – Hendrik SchaperWritten-By – P. Schilling* Fünfte Dimension A4 5:11 Written By – Armin Sabol/P. SchillingWritten-By – Armin Sabol, P. Schilling* 10.000 Punkte A5 Keyboards – Hendrik SchaperRecorder [Sound, Tonmeister] – Frank ReinkeWritten By – 3:16 Armin Sabol/P. SchillingWritten-By – Armin Sabol, P. Schilling* Einsam Überleben B1 4:03 Written By – Armin Sabol/Ulf KrügerWritten-By – Armin Sabol, Ulf Krüger Party Im Vulkan B2 Bass – Anselm KlugeEngineer [Aufnahme] – Geoff Peacey*, Peter SchmidtWritten-By – P. 4:46 Schilling* Terra Titanic B3 Bass – Tissy ThiersEngineer [Aufnahme] – Geoff Peacey*, Peter SchmidtWritten By – P. 5:03 Schilling/Ulf KrügerWritten-By – P. Schilling*, Ulf Krüger 120 Grad B4 4:40 Written By – Armin Sabol/P. SchillingWritten-By – Armin Sabol, P. Schilling* Companies, etc. Manufactured By – Record Service GmbH Phonographic Copyright (p) – WEA Musik GmbH Copyright (c) – WEA Musik GmbH Made By – WEA Musik GmbH Pressed By – Record Service Alsdorf Recorded At – Peer Studio Mixed At – Peer Studio Mastered -

V. 50, No. 8, September 23, 1983
Friday, September 23, 1983 - Bryant College's Student Newspaper - Volume SO, Number 8 Small Business Development Center benefits business,students,faculty By Robin DeMattia mem ber of the Strategic E onomic OJ T"~ Archway Stqff Development Commission which will report Can you imagine pending four years it findings on October 15th of this yea r. Say I studying at Bryant. arguing over grades with Fogarty.'" hope to make a real impact on thc leachers, walking through tbe balls with other economy of Rhode Island." st udents. graduating and then coming back to. The SBDC runs 0.0 a fifty-fifty matching ot work at Bryant as a member of the funds between Bryant CoUege and the Smal. administration? Well that's exactly what Ray Busine Administration. There is no harge Fogarty did. fo r the counseling provided by the SBOC.! Fogarty i a 1979 graduate of Bryant with a Since July of this year the Ce nter ha . helped major in Accounting. He was hired in July of more than 150 small businesses. Not only are 1979 as the Assistant to tb Controller of there over eighty consultants willing to help Bryant College. For the past four years he has businesses but Bryant has an active staff of dealt wi th linancial reports. analyses. and faculty aJ o. Mr. RichaTd on, Ms. Rile ,and transactions pertaimng to the financia~ 'Ms, Notorantonio are just a few of the Bryarll operations of the coUege. But on June I, 1983. faculty that have lent their services to the Ray was appoiDled PJogram Coordinator for Center. -

Descriptor Control of Sound Transformations and Mixture
Descriptor Control of Sound Transformations and Mosaicing Synthesis Graham Coleman TESI DOCTORAL UPF / 2015 Directors de la tesi: Dr. Xavier Serra i Dr. Jordi Bonada Department of Information and Communication Technologies By Graham Coleman and licensed under Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported You are free to Share { to copy, distribute and transmit the work Under the following conditions: • Attribution { You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work). • Noncommercial { You may not use this work for commercial pur- poses. • No Derivative Works { You may not alter, transform, or build upon this work. With the understanding that: Waiver { Any of the above conditions can be waived if you get permission from the copyright holder. Public Domain { Where the work or any of its elements is in the public domain under applicable law, that status is in no way affected by the license. Other Rights { In no way are any of the following rights affected by the license: • Your fair dealing or fair use rights, or other applicable copyright exceptions and limitations; • The author's moral rights; • Rights other persons may have either in the work itself or in how the work is used, such as publicity or privacy rights. Notice { For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to this web page. The court's PhD was appointed by the rector of the Universitat Pompeu Fabra on .............................................., 2016. -

Evaluation of Human Reliability on the Basis of Operational Experience
Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) mbH [Society for Systems and Reactor Safety Inc] Evaluation of Human Reliability on the Basis of Operational Experience Dissertation GRS-170 Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) mbH [Society for Systems and Reactor Safety Inc] Evaluation of Human Reliability on the Basis of Operational Experience Dissertation of Oliver Sträter August 2000 GRS-170 ISBN 3-931995-37-2 Note: The printout is tested on various printers showing problems that cannot be covered in advance. In case the printout has some layout failures please · try to adjust the printer-font settings into either “loading true-type fonts as bitmap” or “loading true-type fonts as graphics” in case the text has some misprints (like incorrect hyphenation) · try to adjust the graphic settings in case the pictures and/or tables are incorrect or improper (graphics grid, graphics color settings in the printer driver) · consider that the document was formatted for European standard pages sized A4 (21 cm * 29,7 cm). To assure the original size of the document, please disable the check-box “Fit to page”. To adjust the page to other formats, please enable the check-box “Fit to page” in the Print Dialog Box of Acrobat Reader. · see for further Information "www.lfe.mw.tum.de/forschung/mms/cahr". This book is a complete Translation of the Report GRS-138 "Beurteilung der menschlichen Zuverlässigkeit auf Basis von Betriebserfahrung" published January 1997 by GRS, Co- logne/Germany (ISBN 3-923875-95-9). All rights reserved. No part of this book may be used or reproduced in any manner whatsoever without written permission, except in the case of referred quotations.