DOCSLIB.ORG

ON FRACTIONAL HELMHOLTZ EQUATIONS M. S. Samuel

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ON FRACTIONAL HELMHOLTZ EQUATIONS M. S. Samuel View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Bulgarian Digital Mathematics Library at IMI-BAS ON FRACTIONAL HELMHOLTZ EQUATIONS M. S. Samuel ¤ and Anitha Thomas ¤¤ Abstract In this paper we derive an analytic solution for the fractional Helmholtz equation in terms of the Mittag-Le²er function. The solutions to the frac- tional Poisson and the Laplace equations of the same kind are obtained, again represented by means of the Mittag-Le²er function. In all three cases the solutions are represented also in terms of Fox's H-function. MSC 2010: 26A33, 33E12, 33C60, 35R11 Key Words and Phrases: fractional Helmholtz equation, Caputo frac- tional derivative, Weyl fractional derivative, Mittag-Le²er function, Fox's H-function 1. Introduction The Helmholtz equation r2ª(x; y; z) + k2ª(x; y; z) = 0 is named after Hermann Von Helmholtz (1821-1894). It represents the time-independent form of the wave equation or di®usion equation obtained while applying the technique of separation of variables to reduce the complexities of the solu- tion procedure of the original equations. The two-dimensional Helmholtz equation appears in physical phenomena and engineering applications such as heat conduction, acoustic radiation, water wave propagation and even in biology. It plays essential role for estimating the geodesic sea floor proper- ties, the proper prediction of acoustic propagation in shallow water as well as at low frequencies, for solutions provided to such problems, we refer to °c 2010, FCAA { Diogenes Co. (Bulgaria). All rights reserved. 296 M.S. Samuel, A. Thomas Liu et al. [9]. The Helmholtz equation solves also problems in pattern for- mation of animal coating, see Murray and Myerscough [12]; in electromag- netics, where its two-dimensional form appears as the governing equation for waveguide problems, etc. Di®erent numerical methods like the Ritz-Galerkin method (Itoh [7]), the surface integral equation method and the ¯nite element method have been employed to solve this equation. In the Ritz-Galerkin method and in the integral equation method, the application of the method of moments to the solution of the integral equation leads to homogeneous systems of linear equations. The matrix coe±cients of these systems of equations are given by in¯nite summation in the case of the Ritz-Galerkin method, while in the surface integral method, integrals containing Hankel functions have to be numerically computed, and this consumes large central processing unit time. In the ¯nite element method (we refer e.g. to Pregla [16]), the basis functions representing the ¯eld singularities lead to matrices in the generalized eigenvalue problem, whose coe±cients have to be computed by means of numerical integration. If we ignore these ¯eld singularities when applying ¯nite element method, inaccurate results may be obtained. To reduce the memory requirements and inaccuracy, it is advantageous to reformulate the boundary value problem for the Helmholtz equation as an initial value problem of fractional order ®, where 1 < <(®) · 2. In this paper, we introduce a model fractional Helmholtz equation in two-dimensions, in which both the space variables x and y are allowed to take fractional order changes. This model is suitable for the study of elec- tromagnetic waves propagating in the upper halfspace of the cartesian plane and is de¯ned as ® ® 2 ¡1Dx N(x; y) + 0Dy N(x; y) + k N(x; y) = ©(x; y); (1) k > 0; x 2 <; y 2 <+; 1 < <(®) · 2; where k is the wave number given 2¼ by k = ¸ , ¸ is the wavelength, N(x; y) is the ¯eld variable of interest, which could be acoustic pressure, wave elevation or electromagnetic poten- tial, among many other possibilities and ©(x; y) is a non-linear function in ® the ¯eld. Here ¡1Dx denotes the Weyl fractional derivative of order ®, and ® 0Dy is the Caputo fractional derivative of order ®, which are two alternative ® forms of the Riemann-Liouville fractional derivative aDx of order ®: m Z t ® R ® 1 d N(x; u) aDt N(x; t) := a Dt N(x; t) = m ®¡m+1 du; (2) ¡(m ¡ ®) dt a (t ¡ u) that are de¯ned as follows: ON FRACTIONAL HELMHOLTZ EQUATIONS 297 Z t (m) ® C ® 1 N (x; u) 0Dt N(x; t) := 0 Dt N(x; t) = ®¡m+1 du; (3) ¡(m ¡ ®) 0 (t ¡ u) m Z t ® 1 d N(x; u) ¡1Dt N(x; t) = m ®¡m+1 du; (4) ¡(m ¡ ®) dt ¡1 (t ¡ u) dm th where t > 0; m ¡ 1 < ® · m; m 2 N, and dtm N(x; t) is the m derivative of order m of the function N(x; t) with respect to t. The Mittag-Le²er function is a special function having an essential role in the solutions of fractional order integral and di®erential equations. This function is frequently used recently in modeling phenomena of fractional order appearing in physics, biology, engineering and applied other sciences. After being introduced and studied by Mittag-Le²er (1903-1905), Wiman (1905) and Agarwal (1953), the Mittag-Le²er function, in its two forms: X1 zn E (z) = ; ® 2 C; <(®) > 0; (5) ® ¡(n® + 1) n=0 X1 zn E (z) = ; ®; ¯ 2 C; <(®) > 0; <(¯) > 0; (6) ®;¯ ¡(n® + ¯) n=0 has been studied in details by Dzherbashyan [1]. Both functions (5)-(6) are 1 entire functions of order ½ = ® and type σ = 1: Firstly in 1920, Hille and Tamarkin [6] have presented a solution of the Abel-Volterra type integral equation Z ¸ x Á(t) Á(x) ¡ 1¡® dt = f(x); 0 < x < 1; ¡(®) 0 (x ¡ t) in terms of Mittag-Le²er function. We are motivated by the recent works of Saxena-Mathai-Haubold ([18], [19], [20]) on fractional kinetic and frac- tional di®usion equations to obtain solutions in terms of the Mittag-Le²er function. For an extensive bibliography on these kind of studies, see e.g. in Povstenko [14]. The objective of this paper is to represent a solution of the fractional Helmholtz equation (1) in terms of the Mittag-Le²er function as well as in Fox's H-function, using the Laplace and Fourier transforms and their inverse transforms. Mathematically, the Poisson and the Laplace equations are two special cases of the Helmholtz equation. We apply this fact also to the fractional case. In Section 3, we derive the solution of the fractional Laplace equation in Mittag-Le²er function and Fox's H-function. Section 4 298 M.S. Samuel, A. Thomas is devoted to the fractional Poisson equation. The solution of the fractional Helmholtz equation is given in Section 5. Its proof and the convergence and the series representation of the H-function are given in the Appendix. 2. Mathematical preliminaries The main results on Mittag-Le²er functions (5), (6) are available in the handbook of Erd¶elyiet al. [4], the monographs by Dzherbashyan ([1], [2]), some recent books as by Kiryakova (1994), Podlubny [15], Kilbas, Srivastava and Trujillo (2006), Mainardi (2010), among them see e.g. the book of Mathai-Saxena-Haubold [10]. The H-function is de¯ned by means of a Mellin-Barnes type integral in the following manner (we refer to Mathai- Saxena-Haubold [10]), " ¯ # ¯(ap;Ap) m;n ¯ Hp;q (z) z ¯ (bq;Bq) n o n o (7) Z Qm Qn ¡(bj + Bjs) ¡(1 ¡ bj ¡ Bjs) 1 j=1 j=0 ¡s = nQ o nQ o z ds; 2¼i L q p j=m+1 ¡(1 ¡ bj ¡ Bjs) j=n+1 ¡(aj + Ajs) where: an empty product is always interpreted as unity; m; n; p; q 2 N0 with 0 · n · p; 1 · m · q; Aj;Bj 2 <+; ai; bj 2 < or C; i = 1; : : : ; p; j = 1; : : : ; q such that Ai(bj + k) 6= Bj(ai ¡ l ¡ 1); k; l 2 N0; i = 1; : : : ; n; j = 1; : : : ; m; and we employ the usual notations: N0 = (0; 1;:::; ); < = (¡1; 1); <+ = (0; 1) and C being the complex number ¯eld. For the details about the contour L and the existence conditions see, Mathai-Saxena-Haubold [10], Prudnikov-Brychkov-Marichev [17] and Kilbas-Saigo [8]. The Wright's generalized hypergeometric function (Wright ([21], [22]) is de¯ned by the series representation h i Qp s h ¯ i X1 ¡(aj + Ajs) z (ap;Ap) j=1 pÃq(z) =p Ãq z¯ = h i ; (bq;Bq) Qq r=0 j=1 ¡(bj + Bjs) s! Pq where z 2 C; aj; bj 2 C;Aj;Bj 2 <+; i = 1; :::; p; j = 1; :::; q; j=1 bj ¡ Pp j=1 Aj > ¡1; C is the complex number ¯eld. The Mittag-Le²er function is a special case of this function, " ¯ # " ¯ # ¯(1;1) ¯(0;1) ¯ 1;1 ¯ E®;¯(z) = 1Ã1 z¯ = H1;2 ¡z¯ : (8) (¯;®) (0;1)(1¡¯;®) ON FRACTIONAL HELMHOLTZ EQUATIONS 299 The Laplace transform of the function N(x; t) with respect to t is Z 1 L [N(x; t)] = e¡stN(x; t)dt = N~(x; s); x 2 <; <(s) > 0; (9) 0 and its inverse transform with respectZ to s is given by h i 1 γ+i1 L¡1 N~(x; s) = estN~(x; s)ds = N(x; t); (10) 2¼i γ¡i1 γ being a ¯xed real number. The Fourier transform of a function N(x; t) with respect to x is de¯ned as Z 1 F [N(x; t)] = eipxN(x; t)dx = N ¤(p; t); x 2 <; (11) ¡1 the inverse Fourier transform with respect to p: Z 1 1 F ¡1 [N ¤(p; t)] = e¡ipxN ¤(p; t) dp = N(x; t): (12) 2¼ ¡1 The space of functions for the above two transforms is LF = L(<+) £ F (<), where L(<+) is the space of summable functions on <+ with norm R 1 jjfjj = 0 jf(t)jdt < 1 and F (<) is the space of summable functions R 1 on < with norm jjfjj = ¡1 jf(t)jdt < 1: From Saxena-Mathai-Haubold [10] and Prudnikov-Brychkov-Marichev [17], the cosine transform of the H- function is given by Z " ¯ # 1 ¯(ap;Ap) ½¡1 m;n ¹¯ t cos(kt)Hp;q at ¯ dt (13) 0 (b ;B ) q q " # ¯(1¡b ;B )( 1+½ ; ¹ ) ¹ ¯ q q 2 2 ¼ n+1;m p ¯ = ½ Hq+1;p+2 ¯ ; k a (½;¹); (1¡a ;A );( 1+½ ; ¹ ) · ¸ · p¸ p 2 2 b a ¡ 1 where < ½ + ¹ min ( j ) > 0; < ½ + ¹ min ( j ) < 0; jarg aj < 1·j·m Bj 1·j·n Aj 1 Pn Pp Pm Pq 2 ¼θ; θ = j=1 Aj ¡ j=n+1 Aj + j=1 Bj ¡ j=m+1 Bj > 0: The Laplace transform of the Caputo fractional derivative is (see e.g.
Load more

Recommended publications
  • Mahatma Gandhi University, Kottayam, Kerala – 686560
    MAHATMA GANDHI UNIVERSITY, KOTTAYAM, KERALA – 686560 DETAILS OF WORKS PERFORMED IN EACH SECTION OF THE UNIVERSITY Supervisory Officers Section Contact Sl. No. Name of Section Dealing works in the Section E-Mail ID Deputy Number Assistant Registrar Registrar ADMINISTRATION Service matters of Staff: 1. AD A I 0481-2733280 [email protected] JR/DR/AR/SO/Assistants Service Matters of: OA/Clerical Asst./Sto re Asst./Staff Nurse/Roneo Operator/Lab Techn 2. AD A III 0481-2733302 [email protected] (health centre)/Tele. Operator GO Endorsement, Part Time Sweeper engagement Service Matters – FC&D, Drivers, Engineers, Computer Programmers, Security Personal, Anti 3. AD A IV 0481-2733303 [email protected] Harassment Cell, Sanctioning of leave to SO & Above officers AR I (Admn) DR I (Admn) Pension: Bill preparation, Pension certificate 0481-2733239 0481-2733226 4. AD A VIII 0481-27733420 [email protected] issue, Income Tax matters of pensioners Pension Calculation, Pension Sanctioning, NLC [email protected] 5. AD A X Issuing, Family pension, VRS, Restoration of 0481-2333420 commuted portion of pensioners 6. AD A VI Medical Reimbursement 0481-2733305 [email protected] 7. Records Keeping University Records 0481-2733412 DR III All administrative matters related to Inter AR V (Admn) 8. AD A VII 0481-2733425 [email protected] (ADMN) University / Inter School Centres 0481-273 0481-273 3608 Service matters of VC, PVC, Registrar, FO, and [email protected] AR II (Admn.) DR II (Admn) 9. Ad A II 0481-2733281 CE. 0481-2733240 0481-2733227 1 Supervisory Officers Section Contact Sl.
    [Show full text]
  • Malankara Mar Thoma Syrian Church SABHA PRATHINIDHI MANDALAM 2017 - 2020 Address List of Mandalam Members Report Date: 27/07/2017 DIOCESE - ALL Page 1 of 25
    Malankara Mar Thoma Syrian Church SABHA PRATHINIDHI MANDALAM 2017 - 2020 Address List of Mandalam Members Report Date: 27/07/2017 DIOCESE - ALL Page 1 of 25 C001 (NIRANAM - MARAMON DIOCESE) C002 (NIRANAM - MARAMON DIOCESE) C003 (RANNI - NILACKAL DIOCESE) MOST REV. DR. PHILIPOSE MAR MOST REV. DR. JOSEPH MAR THOMA RT. REV. GEEVARGHESE MAR CHRYSOSTOM VALIYA METROPOLITAN METROPOLITAN ATHANASIUS SUFFRAGAN - POOLATHEEN METROPOLITAN JUBILEE HOME, S C S CAMPUS SUFFRAGAN METROPOLITAN MARAMON PO TIRUVALLA PO T M A M, MAR THOMA CENTRE KERALA - 689549 KERALA - 689101 MANDIRAM PO, RANNY 0468-2211212/2211210 0469-2630313,2601210 KERALA - 689672 C004 (MUMBAI DIOCESE) C005 (KOTTARAKARA - PUNALUR C006 (THIRUVANANTHAPURAM - RT. REV. DR. GEEVARGHESE MAR DIOCESE) KOLLAM DIOCESE) THEODOSIUS EPISCOPA RT. REV. DR. EUYAKIM MAR COORILOS RT. REV. JOSEPH MAR BARNABAS MAR THOMA CENTRE, EPISCOPA EPISCOPA SECTOR 10-A,PLOT #18, NAVI MUMBAI OORSALEM ARAMANA,66 KV - VASHI PO SUBSTATION ROAD, MAR THOMA CENTRE, MAHARASHTRA - 400703 PRASANTHI NAGAR, KIZHAKKEKKARA, MANNANTHALA PO, TVPM 022 27669484(O)/27657141(P)/ KOTTARAKARA H O PO KERALA - 695015 C007 (CHENGANNUR - MAVELIKKARA C008 (NORTH AMERICA - EUROPE C009 (ADOOR DIOCESE) DIOCESE) DIOCESE) RT. REV. DR. ABRAHAM MAR PAULOS RT. REV. THOMAS MAR TIMOTHEOS RT. REV. DR. ISAAC MAR PHILOXENOS EPISCOPA EPISCOPA EPISCOPA - - SINAI M.T. CENTRE,2320 S.MERRICK AVE, HERMON ARAMANA, OLIVET ARAMANA, THITTAMEL, MERRICK, NEW YORK 11566 U.S.A ADOOR PO CHENGANNUR PO 001 516 377 3311/ 001 516 377 3322(F) KERALA - 691523 KERALA - 689121 [email protected] 04734 228240(O)/ 229130(P) C010 (CHENNAI - BANGALORE DIOCESE) C011 (DELHI DIOCESE) C012 (KUNNAMKULAM - MALABAR RT. REV. DR. MATHEWS MAR MAKARIOS RT.
    [Show full text]
  • (Kottanad) 6. Re
    1. REV.ABBY K. JOSHUA 8. REV.ABRAHAM C.THARIAN 15. REV.K. S. ABRAHAM * VICAR VICAR KACHANATHU HOUSE, PARUTHIPPARA IMMANUEL MAR THOMA BRISTOL ST THOMAS MAR THOMA AYROOR, PLAKAMON CHURCH CHURCH VELLIYARA PO NALANCHIRA S.O 24, MILLWARD GROVE, FISHPONDS, PATHANAMTHITTA DIST. THIRUVANANTHAPURAM BRISTOL, BS16 5AJ,,UNITED KINGDOM KERALA,INDIA 689612 KERALA,INDIA 695015 Ph: 00441179834521 Mob: 9495662763 Mob: 00447412684278 Ph: 0471 2531344,2533244, 16. REV.K. T. ABRAHAM* Mob: 9745784218 [email protected] KIZHAKKE PARAMPIL, [email protected] 9. REV.ABRAHAM CHACKO VIA-RANNY 2. REV.ABE ABRAHAM VICAR CHELLAKKAD PO VICAR CHUNDAL ST PETERS MAR THOMA PATHANAMTHITTA DIST. VADAKKUPURAM SALEM MAR THOMA CHURCH KERALA,INDIA 689677 CHURCH CHUNDALE PO Ph: 04735-260208 KUMBAZHA WAYANAD Mob: 9847309799 VADAKKUPURAM PO KERALA,INDIA 673123 [email protected] Mob: 8879885139 PATHANAMTHITTA DIST. 17. REV.ABRAHAM KURUVILLA KERALA,INDIA 689653 10. REV.ABRAHAM CHERIAN (MUMBAI) Ph: 0468 2300132,9605894184 VICAR VICAR Mob: 9605232806 VALAKOM ST THOMAS MAR THOMA PHILADELPHIA ST THOMAS, DELAWARE [email protected] CHURCH VALLEY 3. REV.ABEY T. MAMMEN VIA-KOTTARAKARA, 130 GRUBB ROAD, VICAR VALAKOM PO MALVERN, PA 19355,,UNITED STATES OF PATHANAPURAM IMMANUEL MAR THOMA KOLLAM DIST. AMERICA CHURCH KERALA,INDIA 691532 Ph: 610 644 3044 GOVERNMENT HOSPITAL ROAD Ph: 0474 2470527, Mob: 347 791 3148 PATHANAPURAM PO Mob: 9539582907 [email protected] KOLLAM DIST. [email protected] 18. REV. DR.ABRAHAM KERALA,INDIA 689695 11. REV. DR.K. A. ABRAHAM Ph: 0475 2352630, KURUVILLA* (CHELAKOMBU) Mob: 9562330558 THAYIL HOUSE VICAR [email protected] THALAPADY THEVALAKARA HEBRON MAR THOMA MANARCAUD PO 4. REV.ABIN SRAMPICKAL CHURCH KOTTAYAM DIST.
    [Show full text]
  • Accused Persons Arrested in Pathanamthitta District from 24.02.2019To02.03.2019
    Accused Persons arrested in Pathanamthitta district from 24.02.2019to02.03.2019 Name of Name of the Name of the Place at Date & Arresting Court at Sl. Name of the Age & Cr. No & Sec Police father of Address of Accused which Time of Officer, which No. Accused Sex of Law Station Accused Arrested Arrest Rank & accused Designation produced 1 2 3 4 5 6 7 8 9 10 11 510/2019 U/s ADOOR VARGHESE ROY BHAVANAM 23-02-2019 , B RAMESHAN BAILED BY 1 KOCHUKUNJU 57, Male HS JN ADOOR 279 IPC & 185 (PATHANAMT ROY MITHRAPURAM 20:20 SI POLICE MV ACT HITTA) PULLICHANIYIL 509/2019 U/s ADOOR 23-02-2019 , VIPIN BAILED BY 2 ANDROOS ANTONY 46, Male VEEDU PANNIVIZHA HOSPITAL JN 279 IPC & 185 (PATHANAMT 19:30 GOPINATH SI POLICE VILLAGE ADOOR MV ACT HITTA) ANIL BHAVANAM ADOOR THUVAYOOR NORTH NELLIMOOTTIP 23-02-2019 , 506/2019 U/s B RAMESHAN BAILED BY 3 ANIL KUMAR AYYAPPAN 35, Male (PATHANAMT CHITTANIMUKKU PADI 17:35 118(a) of KP Act SI POLICE HITTA) MANAKKALA SOBHA SADANAM ADOOR MOHANAN 23-02-2019 , 505/2019 U/s BAILED BY 4 THANKAPPAN 54, Male ILAMANNOOR KSRTC JN (PATHANAMT B RAMESHAN THAMBI 17:30 118(a) of KP Act POLICE ADOOR HITTA) KONDOOR VEEDU ADOOR GOPALAN VAZHAMUTTAM 23-02-2019 , 504/2019 U/s B RAMESHAN BAILED BY 5 SREEKUMAR 51, Male KSRTC JN (PATHANAMT NAIR VALLIKKODU 17:05 151 CrPC SI POLICE HITTA) VILLAGE RAJEEV BHAVANAM,KARAVA 502/2019 U/s ADOOR ADOOR KSRTC 23-02-2019 , VIPINGOPINAT BAILED BY 6 RAJESH SARASAMMA 29, Male LLIL THARAYIL, SAP 279 IPC & 185 (PATHANAMT JN 15:35 H, SI OF POLICE POLICE COLONY MV ACT HITTA) ,POOTHANKARA NEDIYANNIL VADAKKETHIL NEAR
    [Show full text]
  • Muthoottu Mini Financiers Limited
    Prospectus February 12, 2014 MUTHOOTTU MINI FINANCIERS LIMITED Our Company was originally incorporated on March 18, 1998 as a private limited company under the provisions of the Companies Act, 1956 as Muthoottu Mini Financiers Private Limited. Our Company was converted into a public limited company with the name “Muthoottu Mini Financiers Limited” on receipt of a fresh certificate of incorporation consequent to change in status on November 27, 2013 from the Registrar of Companies, Kerala and Lakshadweep. Our Company is Registered as a Non-Banking Financial Company with the Reserve Bank of India under Section 45-IA of the Reserve Bank of India Act, 1934(2 of 1934) Registered Office:994, Muthoottu Buildings, Kozhencherry, Pathanamthitta – 689 641, Kerala, India; Tel.: +91 468 231 0148; Fax: +91 468 231 4390; Corporate Office: Mini Muthoottu Tech Towers, Kaloor, Cochin – 682017, Kerala, India; Tel.: +91 484 410 1050; Fax: +91 484 410 1027 Website: www.minimuthoottu.com For details of changes in Name and Registered Office, please refer to the chapter History“ and Certain other Corporate Matters”on page 92. Compliance Officer and Contact Person: Ms. Priya Menon Tel.:+91 484 410 1078; Fax: +91 484 410 1027; E-mail: [email protected] PUBLIC ISSUE BY MUTHOOTTU MINI FINANCIERS LIMITED, (“COMPANY” OR “ISSUER”) OF SECURED, REDEEMABLE, NON-CONVERTIBLE DEBENTURES OF FACE VALUE OF `1,000 EACH, (“NCDS”), AGGREGATING UPTO `10,000 LACS, HEREINAFTER REFERRED TO AS THE “BASE ISSUE” WITH AN OPTION TO RETAIN OVER-SUBSCRIPTION UPTO `10,000 LACS AGGREGATING TO A TOTAL OF UPTO `20,000 LACS, HEREINAFTER REFERRED TO AS THE “OVERALL ISSUE SIZE”.
    [Show full text]
  • Malankara Mar Thoma Syrian Church SABHA PRATHINIDHI MANDALAM 2017 - 2020 Address List of Mandalam Members Report Date: 27/07/2017 DIOCESE - ALL Page 1 of 46
    Malankara Mar Thoma Syrian Church SABHA PRATHINIDHI MANDALAM 2017 - 2020 Address List of Mandalam Members Report Date: 27/07/2017 DIOCESE - ALL Page 1 of 46 L001 (NORTH CAROLINA MTC) L002 (LUBBOCK EMMANUEL) L003 (ATLANTA HERMON) MRS. VIJI MATHEW DR. P.JOHN LINCOLN MR. SAGIN K.MAMMAN 12700, RICHMOND RUN DRIVE 2404 YORK AVENUE 1960 SPRING MIST TERRACE RALEIGH, NORTH CAROLINA, 27614 LUBBOCK, TEXAS 79407 LAWRENCE VILLE, GA - 30043 U.S.A U.S.A U.S.A 919-562-8167, 919-795-8409 8067976000, 8064415131 6783760015, 404 229 7054 [email protected] [email protected] [email protected] L004 (TORONTO ST MATHEWS) L005 (BOSTON CARMEL) L006 (CHICAGO ST THOMAS) MR. JACOB JOSEPH MRS. MOLLY KURIAN MR. C.VARUGHESE PHILIP 2507 GRAND OAK TRAIL, OAK VILLE 43 DELANEY STREET,STOW, 1481 AUTUMN TRL. ONTARIO, CANADA- L6MOR7 MA- 01775 ADDISON, IL-60101 001 289 8373171, 001 905 399 6180 U.S.A U.S.A [email protected] 978 897 1260,978 793 1711 630-250-0619, 630-222-7021 [email protected] [email protected] L007 (PHILADELPHIA BETHEL) L008 (CONNECTICUT JERUSALEM) L009 (AUSTIN MTC) MRS. DEENAMMA THOMAS MR. MATHEWS THOMAS MR. SABU T.CHERIYAN 1137 ALTON PLACE 19 CEDAR ST. 2316 PARADISE RIDGE DR. PHILADELPHIA, P.A - 19115 DANBURY, CT-06811 ROUND ROCK, U.S.A U.S.A TEXAS 76665-7911, U.S.A 215 342 0237, 2672707974 203 205 0659, 203 312 4105 512 341 8084, 512 468 4457 [email protected] [email protected] [email protected] L010 (KATTANAM ST THOMAS) L011 (EDMONTON TRINITY) L012 (SALEM M.T.C EASTERN LONG EVANG.
    [Show full text]
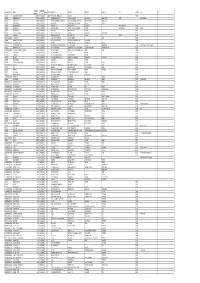
  • Mgl-Di219-Unpaid Share Holders List As on 31-03-2020
    DIVIDEND WARRANT FOLIO-DEMAT ID NAME MICR DDNO ADDRESS 1 ADDRESS 2 ADDRESS 3 ADDRESS 4 CITY PINCODE JH1 JH2 AMOUNT NO 001221 DWARKA NATH ACHARYA 220000.00 192000030 680109 5 JAG BANDHU BORAL LANE CALCUTTA 700007 000642 JNANAPRAKASH P.S. 2200.00 192000034 18 POZHEKKADAVIL HOUSE P.O.KARAYAVATTAM TRICHUR DIST. KERALA STATE 68056 MRS. LATHA M.V. 000691 BHARGAVI V.R. 2200.00 192000035 19 C/O K.C.VISHWAMBARAN,P.B.NO.63 ADV.KAYCEE & KAYCEE AYYANTHOLE TRICHUR DISTRICT KERALA STATE 002679 NARAYANAN P S 2200.00 192000051 35 PANAT HOUSE P O KARAYAVATTOM, VALAPAD THRISSUR KERALA 002976 VIJAYA RAGHAVAN 2200.00 192000056 40 KIZHAKAYIL (H) KEEZHARIYUR P O KOVILANDY KHARRUNNISSA P M 000000 003124 VENUGOPAL M R 2200.00 192000057 41 MOOTHEDATH (H) SAWMILL ROAD KOORVENCHERY THRISSUR GEETHADEVI M V 000000 RISHI M.V. 003292 SURENDARAN K K 2068.00 192000060 44 KOOTTALA (H) PO KOOKKENCHERY THRISSUR 000000 003442 POOKOOYA THANGAL 2068.00 192000063 47 MECHITHODATHIL HOUSE VELLORE PO POOKOTTOR MALAPPURAM 000000 003445 CHINNAN P P 2200.00 192000064 48 PARAVALLAPPIL HOUSE KUNNAMKULAM THRISSUR PETER P C 000000 IN30611420024859 PUSHPA DEVI JAIN 2750.00 192000075 59 A-402, JAWAHAR ENCLAVE JAWAHAR NAGAR JAIPUR 302004 001431 JITENDRA DATTA MISRA 6600.00 192000079 63 BHRATI AJAY TENAMENTS 5 VASTRAL RAOD WADODHAV PO AHMEDABAD 382415 IN30177410163576 Rukaiya Kirit Joshi 2695.00 192000098 82 303 Anand Shradhanand Road Vile Parle East Mumbai 400057 000493 RATHI PRATAP POYYARA 2200.00 192000101 85 10,GREENVILLA,NETAJIPALKARMARG GHATKOPAR(WEST) MUMBAI MAHARASTRA 400084 MR. PRATAP APPUNNY POYYARA 001012 SHARAVATHY C.H. 2200.00 192000102 86 W/O H.L.SITARAMAN, 15/2A,NAV MUNJAL NAGAR,HOUSING CO-OPERATIVE SOCIETY CHEMBUR, MUMBAI 400089 1201090700097429 NANASAHEB BALIRAM SONAWANE 1606.00 192000114 98 2 PALLAWI HSG SOC.
    [Show full text]
  • (Rs.) DATE of TRANSFER to IEPF BALASUBRAMANIAN
    NAME OF ENTITLED SHAREHOLDER LAST KNOWN ADDRESS NATURE OF AMOUNT ENTITLED DATE OF TRANSFER AMOUNT (Rs.) TO IEPF BALASUBRAMANIAN M Snuvy Coop Hsg Soc Ltd Plot No 29 Sector-2 Flat No 10 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 Koperkhai Lane New Mumbai 400701 SBT for FY 2003-2004 VAISHALI PORE Clerk/typist 125 M G Road N M Wadia Bldg Fort Unclaimed and unpaid dividend of 375.00 14-Jan-2021 Mumbai Mumbai 400023 SBT for FY 2003-2004 VINOD MENON Sbi Capital Markets Ltd 202 Maker Tower `e' Cuffe Unclaimed and unpaid dividend of 375.00 14-Jan-2021 Parade Mumbai Mumbai 400005 SBT for FY 2003-2004 GAUTAM KAUSHAL KUMAR Cl/ca S B T 125 M G Road Fort Mumbai Mumbai Unclaimed and unpaid dividend of 375.00 14-Jan-2021 400023 SBT for FY 2003-2004 KANAKARAJ P Sbt Chennai Main 600108 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 SBT for FY 2003-2004 PREMALATHA MANONMANI Sbt Mount Road Madras 600002 Unclaimed and unpaid dividend of 1500.00 14-Jan-2021 SBT for FY 2003-2004 SUBRAMANIAN E N Sbt Mount Road Madras 600002 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 SBT for FY 2003-2004 PRABU K Sbt Mount Road Madras 600002 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 SBT for FY 2003-2004 RAGUNATHAN S 28 Jesurathinam St C S I School Comp Sulur 641402 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 SBT for FY 2003-2004 MOHAMMEDALI M 4a Sabeena St New Ellis Nagar Madurai 625010 Unclaimed and unpaid dividend of 375.00 14-Jan-2021 SBT for FY 2003-2004 VISVANATHAN Periyavila House Arudison Village St Mangad P O K K Unclaimed and unpaid dividend of 750.00 14-Jan-2021 Dist 679001 SBT for FY 2003-2004 PUGALENDI R Plot No.
    [Show full text]
  • Total Amount of Dividend 2619107 Investor First Name Father
    Rane Brake Lining Limited CIN: L63011TN2004PLC054948 Statement of unclaimed and unpaid dividend - AGM 2019 Total amount of dividend 2619107 Folio No. Investor First Name Father/Husband First name Address Country State District Pin Code Amount transferred Date of event DP ID/ Client ID AJAY CHANDEAGARWAL C/O SANJAY KUMAR AGARWAL,33 BHARAT GALI,BAREILLY,BAREILLY INDIA UTTAR PRADESH BAREILLY 6 6.00 17-SEP-2019 ALKA KAPASI C/O SPECOM,POST BOX NO 4070,RUWI MUSCUT, SULTANATE OF OMAN,MUSCUT OMAN NA NA 16 90.00 17-SEP-2019 ALOK KRATHI PLOT NO.584 "RANI ILLAM ",1ST FLOOR, WEST 4TH STREET,K K NAGAR,MADURAI INDIA TAMIL NADU MADURAI 625020 18 600.00 17-SEP-2019 AMBALAL 22 BANK OF INDIA STAFF CO OP,HOUSING SOCIETY SCHEME NO 2,NAVRANGPURA,AHMEDABAD INDIA GUJARAT AHMEDABAD 380009 21 150.00 17-SEP-2019 AMIRUDDIN AL-BAHR CO-OP HOUSING SOCIETY,FLAT NO 301,170-E VEER SAVARKAR MARG, MAHIM,MUMBAI INDIA MAHARASHTRA MUMBAI 400016 27 150.00 17-SEP-2019 ANEJA B-1 BHAGYANAGAR COMPLEX,RTC 'X' ROAD,,HYDERABAD INDIA ANDHRA PRADESH HYDERABAD 35 60.00 17-SEP-2019 ANIL MEHRAY C/O GIFTS LAND,45 M G ROAD,CIVIL LINES,ALLAHABAD INDIA UTTAR PRADESH ALLAHABAD 40 120.00 17-SEP-2019 ANJALI CAGARWAL C/O NARESH CHANDRA AGARWAL,*SARAFF*,NEHRU ROAD,FARRUKHABAD INDIA UTTAR PRADESH FARUKHABAD 47 6.00 17-SEP-2019 ANJANA CTILESARA PHENOLITE ELECTROHEAT PVT LTD,NO.10,I DIVISION,YESWANTHPUR,BANGALORE INDIA KARNATAKA BANGALORE 560022 48 12.00 17-SEP-2019 ANJOO TANDON C/O MR UDAI TANDON,NO 7/126,SWAROOP NAGAR,KANPUR INDIA UTTAR PRADESH KANPUR NAGAR 49 60.00 17-SEP-2019 ANNA CFMASCARENHAS
    [Show full text]
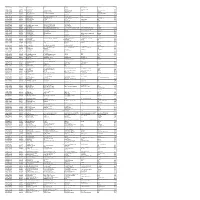
  • Mgl- Di318-Unpaid Shareholders List As on 30
    FOLIO-DEMAT ID DWNO NETDIV NAME ADDRESS 1 ADDRESS 2 ADDRESS 3 City PIN IN30223610002208 183013893 6.00 SRIVALSAN PILLAI 219 B POCKET-C SIDDHARTH EXTN NEW DELHI 110044 IN30011811279255 183014386 250.00 SUNITA BHATIA C-79 IIND FLOOR ASHOK VIHAR PHASE-I DELHI 110052 IN30051322499953 183017925 4168.00 RAVI KUKREJA 40 ALFREDA AVENUE MORLEY P CODE 6062 PERTH WESTERN AUSTRALIA 111111 IN30048414768889 183018413 1.00 SANJAY GUPTA HOUSE NO 215 SECTOR 8 FARIDABAD HARYANA FARIDABAD 121004 IN30292710252507 183022658 500.00 DINESH CHAWLA HOUSE NO 1264 ARYAN ENCLAVE SECTOR 51 B CHANDIGARH 160047 IN30048417042869 183024408 1.00 LIBI JACOB OOMMEN V-14 GROUND FLOOR SECTOR 12 NOIDA UTTAR PRADESH 201301 1202060000069367 183011221 50.00 INDERA DEVI 7232 ROOP NAGAR NEW DELHI 110007 IN30160411531206 183011520 100.00 KISHAN CHAND H NO 340 BHAI PARMANAND COLONY MUKHERJEE NAGAR DELHI DELHI 110009 IN30051323019723 183012755 20.00 SUMAN HASIJA B 45 DAYANAND COLONY NEAR M C D SCHOOL LAJAPT NAGAR 4 NEW DELHI SOUTH DELHI NEW DELHI DELHI 110024 IN30371911001871 183012829 188.00 MADAN MOHAN C-140 BLOCK C DEFENCE COLONY NEW DELHI NEW DELHI NEW DELHI 110024 1201090002105893 183017360 8.00 POONAM SHARMA H. NO. 227 GALI NO. 4 DURGAPURI EXTN. DELHI 110093 IN30223610829087 183019526 10.00 UTTAM SINGH A A-10 KENDRIYA VIHAR SECTOR-56 GURGAON 122011 IN30154955949749 183010423 130.00 SAMIR GILANI UNIT 905 9TH FLOOR PLATINUM TOWER JLT CLUSTER 1 PO BOX 450132 DUBAI UAE 0 1203280000222453 183010486 25.00 BENOY CHERIAN . P O BOX 10315 DANWAY QATAR DOHA 0 1203280000472718 183010500 31.00 EMIL K PAUL . ALPHA LINK TECHNOLOGY W L L P O BOX 82584 DOHA 0 1203280000475343 183010501 250.00 MINNETTE AURELIA ANDRADE .
    [Show full text]
  • Mahatma Gandhi University, Kottayam, Kerala – 686560
    MAHATMA GANDHI UNIVERSITY, KOTTAYAM, KERALA – 686560 DETAILS OF WORKS PERFORMED IN EACH SECTION OF THE UNIVERSITY Supervisory Officers Name of Section Contact Sl. No. Dealing works in the Section E-Mail ID Deputy Section Number Assistant Registrar Registrar ADMINISTRATION Service matters of Staff: 1. AD A I 0481-2733280 [email protected] JR/DR/AR/SO/Assistants Service Matters of: OA/Clerical Asst./Store Asst./Staff Nurse/Roneo Operator/Lab Techn 2. AD A III (health centre)/Tele. Operator 0481-2733302 [email protected] GO Endorsement, Part Time Sweeper engagement Service Matters – FC&D, Drivers, Engineers, Computer Programmers, Security Personal, Anti 3. AD A IV 0481-2733303 [email protected] Harassment Cell, Sanctioning of leave to SO & AR I (Admn) DR I (Admn) Above officers 0481-2733239 0481-2733226 Pension: Bill preparation, Pension certificate 4. AD A VIII 0481-27733420 [email protected] issue, Income Tax matters of pensioners Pension Calculation, Pension Sanctioning, NLC [email protected] 5. AD A X Issuing, Family pension, VRS, Restoration of 0481-2333420 commuted portion of pensioners 6. AD A VI Medical Reimbursement 0481-2733305 [email protected] 7. Records Keeping University Records 0481-2733412 DR III All administrative matters related to Inter AR V (Admn) 8. AD A VII 0481-2733425 [email protected] (ADMN) University / Inter School Centres 0481-273 0481-273 3608 Service matters of VC, PVC, Registrar, FO, and [email protected] AR II (Admn.) DR II (Admn) 9. Ad A II 0481-2733281 CE. 0481-2733240 0481-2733227 1 Supervisory Officers Name of Section Contact Sl.
    [Show full text]
  • Aqar 2017-18
    ANNUAL QUALITY ASSURANCE REPORT (AQAR) 2017-18 BISHOP ABRAHAM MEMORIAL COLLEGE THURUTHICAD Submitted to: National Accreditation and Assessment Council (NAAC) P.O. Box No. 1075, Opp: NLSIU, Nagarbhavi, Bangaluru, 560072 India BISHOP ABRAHAM MEMORIAL COLLEGE, THURUTHICAD AQAR 2017 – 18 PART – A 1. Details of the Institution 1.1 Name of the Institution BISHOP ABRAHAM MEMORIAL COLLEGE 1.2 Address Line 1 THURUTHICADU P. O Address Line 2 THIRUVALLA City/Town PATHANAMTHITTA State KER ALA Pin Code 689597 [email protected] Institution e-mail address Contact Nos. 04692682820 / 04692682241 Name of the Head of the Institution: Dr. Alex Mathew Tel. No. with STD Code: 04692682820 (Office) / 0469 663283 (Residence) Mobile: 09495185128 Name of the IQAC Co-ordinator: Dr . Thomson K. Alex Mobile: 9400947721 IQAC e-mail address: [email protected] Bishop Abraham Memorial College AQAR 2017 - 18 2 1.3 NAAC Track ID: KLCOGN13714 1.4 NAAC Executive Committee No. EC/47/A&A/05 1.5 Website address: WWW.bamcollege.org Web-link of the AQAR: http://www.bamcollege.org/aqar.php 1.6 Accreditation Details Year of Validity Sl. No. Cycle Grade CGPA Accreditation Period 1 1st Cycle B 2.35 2009 2014 2 2nd Cycle B 2.55 2015 2020 3 3rd Cycle 4 4th Cycle 1.7 Date of Establishment of IQAC: DD/MM/YYYY 11 / 08 / 2009 1.8 AQAR for the year 2017 - 18 1.9 Details of the previous year’s AQAR submitted to NAAC after the latest Assessment and Accreditation by NAAC ((for example AQAR 2010-11submitted to NAAC on 12-10-2011) i.
    [Show full text]