Predicting the Binding Preference of Transcription Factors to Individual
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Identification of Foxr2 As an Oncogene in Medulloblastoma
Published OnlineFirst March 5, 2014; DOI: 10.1158/0008-5472.CAN-13-1523 Cancer Tumor and Stem Cell Biology Research Identification of FoxR2 as an Oncogene in Medulloblastoma Hideto Koso1,2, Asano Tsuhako1, Eli Lyons1, Jerrold M. Ward2, Alistair G. Rust3, David J. Adams3, Nancy A. Jenkins2,4, Neal G. Copeland2,4, and Sumiko Watanabe1 Abstract Medulloblastoma is the most common pediatric brain tumor, and in 25% of cases, it is driven by aberrant activation of the Sonic Hedgehog (SHH) pathway in granule neuron precursor (GNP) cells. In this study, we identified novel medulloblastoma driver genes through a transposon mutagenesis screen in the developing brain of wild-type and Trp53 mutant mice. Twenty-six candidates were identified along with established driver genes such as Gli1 and Crebbp. The transcription factor FoxR2, the most frequent gene identified in the screen, is overexpressed in a small subset of human medulloblastoma of the SHH subtype. Tgif2 and Alx4, 2 new putative oncogenes identified in the screen, are strongly expressed in the SHH subtype of human medulloblas- toma. Mutations in these two genes were mutually exclusive with mutations in Gli1 and tended to cooccur, consistent with involvement in the SHH pathway. Notably, Foxr2, Tgif2, and Alx4 activated Gli-binding sites in cooperation with Gli1, strengthening evidence that they function in SHH signaling. In support of an oncogenic function, Foxr2 overexpression transformed NIH3T3 cells and promoted proliferation of GNPs, the latter of which was also observed for Tgif2 and Alx4. These findings offer forward genetic and functional evidence associating Foxr2, Tgif2, and Alx4 with SHH subtype medulloblastoma. -

TGIF2 Monoclonal Antibody (M06), Clone 6A8
TGIF2 monoclonal antibody (M06), clone 6A8 Catalog # : H00060436-M06 規格 : [ 100 ug ] List All Specification Application Image Product Mouse monoclonal antibody raised against a partial recombinant Western Blot (Cell lysate) Description: TGIF2. Immunogen: TGIF2 (NP_068581, 131 a.a. ~ 236 a.a) partial recombinant protein with GST tag. MW of the GST tag alone is 26 KDa. Sequence: SMPLHSGQGEKPAAPFPRGELESPKPLVTPGSTLTLLTRAEAGSPTGG LFNTPPPTPPEQDKEDFSSFQLLVEVALQRAAEMELQKQQDPSLPLLHT enlarge PIPLVSENP Western Blot (Recombinant protein) Host: Mouse Immunofluorescence Reactivity: Human Isotype: IgG2a Kappa Quality Control Antibody Reactive Against Recombinant Protein. Testing: enlarge Sandwich ELISA (Recombinant protein) enlarge ELISA Western Blot detection against Immunogen (37.4 KDa) . Storage Buffer: In 1x PBS, pH 7.4 Storage Store at -20°C or lower. Aliquot to avoid repeated freezing and thawing. Instruction: MSDS: Download Datasheet: Download Applications Western Blot (Cell lysate) Page 1 of 3 2020/3/20 TGIF2 monoclonal antibody (M06), clone 6A8 Western Blot analysis of TGIF2 expression in IMR-32 ( Cat # L008V1 ). Protocol Download Western Blot (Recombinant protein) Protocol Download Immunofluorescence enlarge this image Immunofluorescence of monoclonal antibody to TGIF2 on HeLa cell. [antibody concentration 10 ug/ml] Sandwich ELISA (Recombinant protein) Detection limit for recombinant GST tagged TGIF2 is approximately 0.3ng/ml as a capture antibody. Protocol Download ELISA Gene Information Entrez GeneID: 60436 GeneBank NM_021809 Accession#: Protein NP_068581 Accession#: Gene Name: TGIF2 Gene Alias: - Page 2 of 3 2020/3/20 Gene TGFB-induced factor homeobox 2 Description: Omim ID: 607294 Gene Ontology: Hyperlink Gene Summary: The protein encoded by this gene is a DNA-binding homeobox protein and a transcriptional repressor. The encoded protein appears to repress transcription by recruiting histone deacetylases to TGF beta- responsive genes. -

Rapid Evolution of Mammalian X-Linked Testis-Expressed Homeobox Genes
Copyright 2004 by the Genetics Society of America DOI: 10.1534/genetics.103.025072 Rapid Evolution of Mammalian X-Linked Testis-Expressed Homeobox Genes Xiaoxia Wang and Jianzhi Zhang1 Department of Ecology and Evolutionary Biology, University of Michigan, Ann Arbor, Michigan 48109 Manuscript received November 26, 2003 Accepted for publication February 11, 2004 ABSTRACT Homeobox genes encode transcription factors that function in various developmental processes and are usually evolutionarily conserved in their sequences. However, two X-chromosome-linked testis-expressed homeobox genes, one from rodents and the other from fruit flies, are known to evolve rapidly under positive Darwinian selection. Here we report yet another case, from primates. TGIFLX is an X-linked homeobox gene that originated by retroposition of the autosomal gene TGIF2, most likely in a common ancestor of rodents and primates. While TGIF2 is ubiquitously expressed, TGIFLX is exclusively expressed in adult testis. A comparison of the TGIFLX sequences among 16 anthropoid primates revealed a signifi- cantly higher rate of nonsynonymous nucleotide substitution (dN) than synonymous substitution (dS), strongly suggesting the action of positive selection. Although the high dN/dS ratio is most evident outside ف the homeobox, the homeobox has a dN/dS of 0.89 and includes two codons that are likely under selection. Furthermore, the rate of radical amino acid substitutions that alter amino acid charge is significantly greater than that of conservative substitutions, suggesting that the selection promotes diversity of the protein charge profile. More interestingly, an analysis of 64 orthologous homeobox genes from humans and mice shows substantially higher rates of amino acid substitution in X-linked testis-expressed genes than in other genes. -

6 Signaling and BMP Antagonist Noggin in Prostate Cancer
[CANCER RESEARCH 64, 8276–8284, November 15, 2004] Bone Morphogenetic Protein (BMP)-6 Signaling and BMP Antagonist Noggin in Prostate Cancer Dominik R. Haudenschild, Sabrina M. Palmer, Timothy A. Moseley, Zongbing You, and A. Hari Reddi Center for Tissue Regeneration and Repair, Department of Orthopedic Surgery, School of Medicine, University of California, Davis, Sacramento, California ABSTRACT antagonists has recently been discovered. These are secreted proteins that bind to BMPs and reduce their bioavailability for interactions It has been proposed that the osteoblastic nature of prostate cancer with the BMP receptors. Extracellular BMP antagonists include nog- skeletal metastases is due in part to elevated activity of bone morphoge- gin, follistatin, sclerostatin, chordin, DCR, BMPMER, cerberus, netic proteins (BMPs). BMPs are osteoinductive morphogens, and ele- vated expression of BMP-6 correlates with skeletal metastases of prostate gremlin, DAN, and others (refs. 11–16; reviewed in ref. 17). There are cancer. In this study, we investigated the expression levels of BMPs and several type I and type II receptors that bind to BMPs with different their modulators in prostate, using microarray analysis of cell cultures affinities. BMP activity is also regulated at the cell membrane level by and gene expression. Addition of exogenous BMP-6 to DU-145 prostate receptor antagonists such as BAMBI (18), which acts as a kinase- cancer cell cultures inhibited their growth by up-regulation of several deficient receptor. Intracellularly, the regulation of BMP activity at cyclin-dependent kinase inhibitors such as p21/CIP, p18, and p19. Expres- the signal transduction level is even more complex. There are inhib- sion of noggin, a BMP antagonist, was significantly up-regulated by itory Smads (Smad-6 and Smad-7), as well as inhibitors of inhibitory BMP-6 by microarray analysis and was confirmed by quantitative reverse Smads (AMSH and Arkadia). -

The DNA Sequence and Comparative Analysis of Human Chromosome 20
articles The DNA sequence and comparative analysis of human chromosome 20 P. Deloukas, L. H. Matthews, J. Ashurst, J. Burton, J. G. R. Gilbert, M. Jones, G. Stavrides, J. P. Almeida, A. K. Babbage, C. L. Bagguley, J. Bailey, K. F. Barlow, K. N. Bates, L. M. Beard, D. M. Beare, O. P. Beasley, C. P. Bird, S. E. Blakey, A. M. Bridgeman, A. J. Brown, D. Buck, W. Burrill, A. P. Butler, C. Carder, N. P. Carter, J. C. Chapman, M. Clamp, G. Clark, L. N. Clark, S. Y. Clark, C. M. Clee, S. Clegg, V. E. Cobley, R. E. Collier, R. Connor, N. R. Corby, A. Coulson, G. J. Coville, R. Deadman, P. Dhami, M. Dunn, A. G. Ellington, J. A. Frankland, A. Fraser, L. French, P. Garner, D. V. Grafham, C. Grif®ths, M. N. D. Grif®ths, R. Gwilliam, R. E. Hall, S. Hammond, J. L. Harley, P. D. Heath, S. Ho, J. L. Holden, P. J. Howden, E. Huckle, A. R. Hunt, S. E. Hunt, K. Jekosch, C. M. Johnson, D. Johnson, M. P. Kay, A. M. Kimberley, A. King, A. Knights, G. K. Laird, S. Lawlor, M. H. Lehvaslaiho, M. Leversha, C. Lloyd, D. M. Lloyd, J. D. Lovell, V. L. Marsh, S. L. Martin, L. J. McConnachie, K. McLay, A. A. McMurray, S. Milne, D. Mistry, M. J. F. Moore, J. C. Mullikin, T. Nickerson, K. Oliver, A. Parker, R. Patel, T. A. V. Pearce, A. I. Peck, B. J. C. T. Phillimore, S. R. Prathalingam, R. W. Plumb, H. Ramsay, C. M. -

Link Between the Causative Genes of Holoprosencephaly: Zic2 Directly
www.nature.com/scientificreports OPEN Link between the causative genes of holoprosencephaly: Zic2 directly regulates Tgif1 expression Received: 20 October 2017 Akira Ishiguro1,2, Minoru Hatayama1,3, Maky I. Otsuka1 & Jun Aruga1,3 Accepted: 15 January 2018 One of the causal genes for holoprosencephaly (HPE) is ZIC2 (HPE5). It belongs to the zinc fnger Published: xx xx xxxx protein of the cerebellum (Zic) family of genes that share a C2H2-type zinc fnger domain, similar to the GLI family of genes. In order to clarify the role of Zic2 in gene regulation, we searched for its direct target genes using chromatin immunoprecipitation (ChIP). We identifed TGIF1 (HPE4), another holoprosencephaly-causative gene in humans. We identifed Zic2-binding sites (ZBS) on the 5′ fanking region of Tgif1 by in vitro DNA binding assays. ZBS were essential for Zic2-dependent transcriptional activation in reporter gene assays. Zic2 showed a higher afnity to ZBS than GLI-binding sequences. Zic2-binding to the cis-regulatory element near the Tgif1 promoter may be involved in the mechanism underlying forebrain development and incidences of HPE. Holoprosencephaly (HPE) is known as a common forebrain defect in human development1,2. At least 13 chro- mosomal loci are associated with nonsyndromic HPE2,3. SHH, ZIC2, SIX3, and TGIF1 have been identifed to be four causative genes in the HPE loci (HPE3, HPE5, HPE2, and HPE4, respectively) and have been investigated with respect to clinical spectrum4 and genetic interactions5. Among the major HPE-associated genes, the roles of TGIF1 and ZIC2 in forebrain development have been elusive until recently1. However, recent studies have revealed clues as to its roles in forebrain development. -

TGIF2 Human Sirna Oligo Duplex (Locus ID 60436
OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for SR311824 TGF beta induced factor 2 (TGIF2) Human siRNA Oligo Duplex (Locus ID 60436) Product data: Product Type: siRNA Oligo Duplexes Purity: HPLC purified Quality Control: Tested by ESI-MS Sequences: Available with shipment Stability: One year from date of shipment when stored at -20°C. # of transfections: Approximately 330 transfections/2nmol in 24-well plate under optimized conditions (final conc. 10 nM). Note: Single siRNA duplex (10nmol) can be ordered. RefSeq: NM_001199513, NM_001199514, NM_001199515, NM_021809 Components: TGIF2 (Human) - 3 unique 27mer siRNA duplexes - 2 nmol each (Locus ID 60436) Included - SR30004, Trilencer-27 Universal Scrambled Negative Control siRNA Duplex - 2 nmol Included - SR30005, RNAse free siRNA Duplex Resuspension Buffer - 2 ml Summary: The protein encoded by this gene is a DNA-binding homeobox protein and a transcriptional repressor, which appears to repress transcription by recruiting histone deacetylases to TGF beta-responsive genes. This gene is amplified and over-expressed in some ovarian cancers. Alternative splicing results in multiple transcript variants. A related pseudogene has been identified on chromosome 1. Read-through transcription also exists between this gene and the neighboring downstream C20orf24 (chromosome 20 open reading frame 24) gene. [provided by RefSeq, Dec 2010] This product -

Loss of Tgif Function Causes Holoprosencephaly by Disrupting the Shh Signaling Pathway
Loss of Tgif Function Causes Holoprosencephaly by Disrupting the Shh Signaling Pathway Kenichiro Taniguchi1, Anoush E. Anderson1, Ann E. Sutherland2, David Wotton1* 1 Department of Biochemistry and Molecular Genetics and Center for Cell Signaling, University of Virginia, Charlottesville, Virginia, United States of America, 2 Department of Cell Biology, University of Virginia, Charlottesville, Virginia, United States of America Abstract Holoprosencephaly (HPE) is a severe human genetic disease affecting craniofacial development, with an incidence of up to 1/250 human conceptions and 1.3 per 10,000 live births. Mutations in the Sonic Hedgehog (SHH) gene result in HPE in humans and mice, and the Shh pathway is targeted by other mutations that cause HPE. However, at least 12 loci are associated with HPE in humans, suggesting that defects in other pathways contribute to this disease. Although the TGIF1 (TG-interacting factor) gene maps to the HPE4 locus, and heterozygous loss of function TGIF1 mutations are associated with HPE, mouse models have not yet explained how loss of Tgif1 causes HPE. Using a conditional Tgif1 allele, we show that mouse embryos lacking both Tgif1 and the related Tgif2 have HPE-like phenotypes reminiscent of Shh null embryos. Eye and nasal field separation is defective, and forebrain patterning is disrupted in embryos lacking both Tgifs. Early anterior patterning is relatively normal, but expression of Shh is reduced in the forebrain, and Gli3 expression is up-regulated throughout the neural tube. Gli3 acts primarily as an antagonist of Shh function, and the introduction of a heterozygous Gli3 mutation into embryos lacking both Tgif genes partially rescues Shh signaling, nasal field separation, and HPE. -

High-Density Array Comparative Genomic Hybridization Detects Novel Copy Number Alterations in Gastric Adenocarcinoma
ANTICANCER RESEARCH 34: 6405-6416 (2014) High-density Array Comparative Genomic Hybridization Detects Novel Copy Number Alterations in Gastric Adenocarcinoma ALINE DAMASCENO SEABRA1,2*, TAÍSSA MAÍRA THOMAZ ARAÚJO1,2*, FERNANDO AUGUSTO RODRIGUES MELLO JUNIOR1,2, DIEGO DI FELIPE ÁVILA ALCÂNTARA1,2, AMANDA PAIVA DE BARROS1,2, PAULO PIMENTEL DE ASSUMPÇÃO2, RAQUEL CARVALHO MONTENEGRO1,2, ADRIANA COSTA GUIMARÃES1,2, SAMIA DEMACHKI2, ROMMEL MARIO RODRÍGUEZ BURBANO1,2 and ANDRÉ SALIM KHAYAT1,2 1Human Cytogenetics Laboratory and 2Oncology Research Center, Federal University of Pará, Belém Pará, Brazil Abstract. Aim: To investigate frequent quantitative alterations gastric cancer is the second most frequent cancer in men and of intestinal-type gastric adenocarcinoma. Materials and the third in women (4). The state of Pará has a high Methods: We analyzed genome-wide DNA copy numbers of 22 incidence of gastric adenocarcinoma and this disease is a samples and using CytoScan® HD Array. Results: We identified public health problem, since mortality rates are above the 22 gene alterations that to the best of our knowledge have not Brazilian average (5). been described for gastric cancer, including of v-erb-b2 avian This tumor can be classified into two histological types, erythroblastic leukemia viral oncogene homolog 4 (ERBB4), intestinal and diffuse, according to Laurén (4, 6, 7). The SRY (sex determining region Y)-box 6 (SOX6), regulator of intestinal type predominates in high-risk areas, such as telomere elongation helicase 1 (RTEL1) and UDP- Brazil, and arises from precursor lesions, whereas the diffuse Gal:betaGlcNAc beta 1,4- galactosyltransferase, polypeptide 5 type has a similar distribution in high- and low-risk areas and (B4GALT5). -
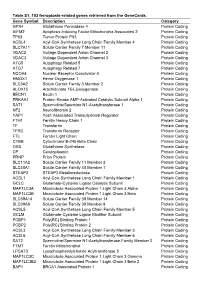
Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein -

Functional Analysis of Genomic Variation and Impact on Molecular and Higher Order Phenotypes Ashutosh Kumar Pandey University of Tennessee Health Science Center
University of Tennessee Health Science Center UTHSC Digital Commons Theses and Dissertations (ETD) College of Graduate Health Sciences 12-2015 Functional Analysis of Genomic Variation and Impact on Molecular and Higher Order Phenotypes Ashutosh Kumar Pandey University of Tennessee Health Science Center Follow this and additional works at: https://dc.uthsc.edu/dissertations Part of the Genetic Phenomena Commons, Genetic Processes Commons, and the Medical Genetics Commons Recommended Citation Pandey, Ashutosh Kumar , "Functional Analysis of Genomic Variation and Impact on Molecular and Higher Order Phenotypes" (2015). Theses and Dissertations (ETD). Paper 359. http://dx.doi.org/10.21007/etd.cghs.2015.0237. This Dissertation is brought to you for free and open access by the College of Graduate Health Sciences at UTHSC Digital Commons. It has been accepted for inclusion in Theses and Dissertations (ETD) by an authorized administrator of UTHSC Digital Commons. For more information, please contact [email protected]. Functional Analysis of Genomic Variation and Impact on Molecular and Higher Order Phenotypes Document Type Dissertation Degree Name Doctor of Philosophy (PhD) Program Biomedical Sciences Track Genetics, Functional Genomics, and Proteomics Research Advisor Robert W. Williams, Ph.D. Committee Hao Chen, Ph.D. Eldon E. Geisert, Ph.D. Ramin Homayouni, Ph.D. David R. Nelson, Ph.D. DOI 10.21007/etd.cghs.2015.0237 Comments Six month embargo expired June 2016 This dissertation is available at UTHSC Digital Commons: https://dc.uthsc.edu/dissertations/359 Functional Analysis of Genomic Variation and Impact on Molecular and Higher Order Phenotypes A Dissertation Presented for The Graduate Studies Council The University of Tennessee Health Science Center In Partial Fulfillment Of the Requirements for the Degree Doctor of Philosophy From The University of Tennessee By Ashutosh Kumar Pandey December 2015 Copyright © 2015 by Ashutosh Kumar Pandey. -

TGF Beta Induced Factor 2 (TGIF2) (NM 021809) Human Untagged Clone Product Data
OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for SC304959 TGF beta induced factor 2 (TGIF2) (NM_021809) Human Untagged Clone Product data: Product Type: Expression Plasmids Product Name: TGF beta induced factor 2 (TGIF2) (NM_021809) Human Untagged Clone Tag: Tag Free Symbol: TGIF2 Vector: pCMV6-Entry (PS100001) E. coli Selection: Kanamycin (25 ug/mL) Cell Selection: Neomycin Fully Sequenced ORF: >NCBI ORF sequence for NM_021809, the custom clone sequence may differ by one or more nucleotides ATGTCGGACAGTGATCTAGGTGAGGACGAAGGCCTCCTCTCCCTGGCGGGCAAAAGGAAGCGCAGGGGGA ACCTGCCCAAGGAGTCGGTGAAGATCCTCCGGGACTGGCTGTACTTGCACCGCTACAACGCCTACCCCTC AGAGCAGGAGAAGCTGAGCCTTTCTGGACAGACCAACCTGTCAGTGCTGCAAATATGTAACTGGTTCATC AATGCCCGGCGGCGGCTTCTCCCAGACATGCTTCGGAAGGATGGCAAAGACCCTAATCAGTTTACCATTT CCCGCCGCGGGGGTAAGGCCTCAGATGTGGCCCTCCCCCGTGGCAGCAGCCCCTCAGTGCTGGCTGTGTC TGTCCCAGCCCCCACCAATGTGCTCTCCCTGTCTGTGTGCTCCATGCCGCTTCACTCAGGCCAGGGGGAA AAGCCAGCAGCCCCTTTCCCACGTGGGGAGCTGGAGTCTCCCAAGCCCCTGGTGACCCCTGGTAGCACAC TTACTCTGCTGACCAGGGCTGAGGCTGGAAGCCCCACAGGTGGACTCTTCAACACGCCACCACCCACACC CCCAGAGCAGGACAAAGAGGACTTCAGCAGCTTCCAGCTGCTGGTGGAGGTGGCGCTACAGAGGGCTGCT GAGATGGAGCTTCAGAAGCAGCAGGACCCATCACTCCCATTACTGCACACTCCCATCCCTTTAGTCTCTG AAAATCCCCAGTAG Restriction Sites: SgfI-MluI ACCN: NM_021809 OTI Disclaimer: Our molecular clone sequence data has been matched to the reference identifier above as a point of reference. Note that