DOCSLIB.ORG

ECE750-TXB Lecture 7: Red-Black Trees, Heaps, and Treaps

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ECE750-TXB Lecture 7: Red-Black Trees, Heaps, and Treaps ECE750-TXB Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. ECE750-TXB Lecture 7: Red-Black Trees, Veldhuizen Heaps, and Treaps [email protected] Red-Black Trees Heaps Todd L. Veldhuizen Treaps [email protected] Bibliography Electrical & Computer Engineering University of Waterloo Canada February 14, 2007 ECE750-TXB Binary Search Trees Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] I Recall that in a binary tree of height h the time required to find or insert an element is O(h). Red-Black Trees Heaps I In the worst case h = n, the number of elements. Treaps I To keep h ∈ O(log n) one needs a balancing strategy. Bibliography I Balancing strategies may be either: I Randomized: e.g. a random insert order results in expected height of c log n with c ≈ 4.311. I Deterministic (in the sense of not random). I Today we will see an example of each: I Red-black trees: deterministic balancing I Treaps: randomized. Also demonstrate persistence and unique representation. ECE750-TXB Red-black trees Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] I Red-black trees are a popular form of binary search tree with a deterministic balancing strategy. Red-Black Trees Heaps I Nodes are coloured red or black. Treaps I Properties of the node-colouring ensure that the longest Bibliography path to a leaf is no more than twice the length of the shortest path. I This ensures height of ≤ 2 log2(n + 1), which implies search, min, max in O(log n) worst-case time. I Insert and Delete can also be performed in O(log n) worst-case time. I Invented by Bayer [2], red-black formulation due to Guibas and Sedgewick [9]. Other sources: [5, 10]. ECE750-TXB Red-Black Trees: Invariants Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] Red-Black Trees Heaps Treaps Balance invariants: I Bibliography 1. No red node has a red child. 2. Every path in a subtree contains the same number of black nodes. ECE750-TXB Red-Black Trees Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] Red-Black Trees Heaps Treaps Bibliography ECE750-TXB Red-Black Trees: Balance I Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] Red-Black Trees Let bh(x) be the number of black nodes along any path Heaps from a node x to a leaf, excluding the leaf. Treaps Bibliography Lemma The number of internal nodes in the subtree rooted at x is at least 2bh(x) − 1. Proof. ECE750-TXB Red-Black Trees: Balance II Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen By induction on height: [email protected] 1. Base case: If x has height 0, then x is a leaf, and Red-Black Trees bh(x) = 0; the number of internal (non-leaf) Heaps bh(x) descendents of x is 0 = 2 − 1. Treaps 2. Induction step: assume the hypothesis is true for height Bibliography ≤ h. Consider a node of height h + 1. From invariant (2), the children have black height either bh(x) − 1 (if the child is black) or bh(x) (if the child is red). By induction hypothesis, each child subtree has at least 2bh(x)−1 − 1 internal nodes. The total number of internal nodes in the subtree rooted at x is therefore ≥ (2bh(x)−1 − 1) + 1 + (2bh(x)−1 − 1) = 2bh(x) − 1. ECE750-TXB Red-Black Trees: Balance Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] Theorem Red-Black Trees A red-black tree with n internal nodes has height at most Heaps Treaps 2 log2(n + 1). Bibliography Proof. Let h be the tree height. From invariant 1 (a red node must have both children black), the black-height of the root must be ≥ h/2. Applying Lemma 1.1, the number of internal nodes n of the tree satisfies n ≥ 2h/2 − 1. Rearranging, h ≤ 2 log2(n + 1). ECE750-TXB Red-Black Trees: Balance Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] I As with all non-randomized binary search trees, balance must be maintained when insert or delete operations are Red-Black Trees performed. Heaps Treaps I These operations may disrupt the invariants, so Bibliography rotations and recolourings are needed to restore them. I Insert for red-black tree: 1. Insert the new key as a red node, using the usual binary tree insert. 2. Perform restructurings and recolourings along the path from the newly added leaf to the root to restore invariants. 3. Root is always coloured black. ECE750-TXB Red-Black Trees: Balance Lecture 7: Red-Black Trees, Heaps, and Treaps I Four cases for red nodes with red children: Todd L. Veldhuizen [email protected] Red-Black Trees Heaps Treaps Bibliography I Restructure/recolour to correct: each of the above cases becomes ECE750-TXB Red-Black Trees: Example Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen I Insertion of [1,2,3,4,5] into a red-black tree: [email protected] Red-Black Trees Heaps Treaps Bibliography I Implementation of rebalancing is straightforward but a bit involved. ECE750-TXB Heaps and Treaps Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. I Treaps are a randomized search tree that combine Veldhuizen TRees and hEAPS. [email protected] Red-Black Trees I First, let’s look at heaps. Heaps I Consider determining the maximum element of a set. Treaps I We could iterate through the array and keep track of Bibliography the maximum element seen so far. Time taken: Θ(n). I We could build a binary tree (e.g. red-black). We can obtain the maximum (minimum) element in O(h) time by following rightmost (leftmost) branches. If tree is balanced, requires O(n log n) time to build the tree, and O(log n) time to retrieve the maximum element. I A heap is a highly efficient data structure for maintaining the maximum element of a set. It is a rudimentary example of a dynamic algorithm/data structure. ECE750-TXB Dynamic Algorithms Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. I A static problem is one where we are given an instance Veldhuizen of a problem to solve, we solve it, and are done (e.g., [email protected] sort an array). Red-Black Trees I A dynamic problem is one where we are given a problem Heaps to solve, we solve it. Treaps I Then the problem is changed slightly and we resolve. Bibliography I ...ad infinitum. I The challenge goes from solving a single instance of a problem to maintaining a solution as the problem is modified. I It is usually more efficient to update the solution than recompute from scratch. I e.g., binary search trees can be viewed as a method for dynamically maintaining an ordered list as elements are inserted and removed. ECE750-TXB Heaps Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen I A heap dynamically maintains the maximum element in [email protected] a collection (or, dually, the minimum element). A binary heap can: Red-Black Trees Heaps I Obtain the maximum element in O(1) time; Treaps I Remove the maximum element in O(log n) time; Bibliography I Insert new element in O(log n) time. Heaps are a natural implementation of the PriorityQueue ADT. I There are several flavours of heaps: binary heaps, binomial heaps, fibonacci heaps, pairing heaps. The more sophisticated of these support merging (melding) two heaps. I We will look at binary heaps. ECE750-TXB Binary Heap Invariants Lecture 7: Red-Black Trees, Heaps, and Treaps 1. A binary heap is a complete binary tree of height h − 1, Todd L. Veldhuizen plus a possibly incomplete level of height h filled from [email protected] left to right. Red-Black Trees 2. The key stored at each node is ≥ the key(s) stored in Heaps its children. Treaps Bibliography ECE750-TXB Binary Heap Lecture 7: Red-Black Trees, Heaps, and Treaps I A binary heap may be stored as a (1-based) array, where Todd L. Veldhuizen I Parent(j) = bj/2c [email protected] I LeftChild(i) = 2 ∗ i Red-Black Trees I RightChild(i) = 2 ∗ i + 1 Heaps I e.g., [17, 11, 13, 9, 6, 2, 12, 4, 3, 1] is an array Treaps representation of the heap: Bibliography ECE750-TXB Heap operations Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] I To insert a key k into the heap: I Place k at the next available position. Red-Black Trees I Swap k with its parent(s) until the heap invariant is Heaps satisfied. (Takes O(log n) time.) Treaps I The maximum element is just the key stored at the Bibliography root, which can be read off in O(1) time. I To delete the maximum element: I Place the key at the last heap position at the root (overwriting the current maximum), and decrease the size of the heap by one. I Choose the largest of the root and its two children, and make this the root; perform this procedure recursively until the heap invariant is satisfied. ECE750-TXB Heap: insert example Lecture 7: Red-Black Trees, Heaps, and Treaps Todd L. Veldhuizen [email protected] Red-Black Trees Heaps I Example: insert 23 into the heap and restore the heap Treaps invariant.
Load more

Recommended publications
  • KP-Trie Algorithm for Update and Search Operations
    The International Arab Journal of Information Technology, Vol. 13, No. 6, November 2016 722 KP-Trie Algorithm for Update and Search Operations Feras Hanandeh1, Izzat Alsmadi2, Mohammed Akour3, and Essam Al Daoud4 1Department of Computer Information Systems, Hashemite University, Jordan 2, 3Department of Computer Information Systems, Yarmouk University, Jordan 4Computer Science Department, Zarqa University, Jordan Abstract: Radix-Tree is a space optimized data structure that performs data compression by means of cluster nodes that share the same branch. Each node with only one child is merged with its child and is considered as space optimized. Nevertheless, it can’t be considered as speed optimized because the root is associated with the empty string. Moreover, values are not normally associated with every node; they are associated only with leaves and some inner nodes that correspond to keys of interest. Therefore, it takes time in moving bit by bit to reach the desired word. In this paper we propose the KP-Trie which is consider as speed and space optimized data structure that is resulted from both horizontal and vertical compression. Keywords: Trie, radix tree, data structure, branch factor, indexing, tree structure, information retrieval. Received January 14, 2015; accepted March 23, 2015; Published online December 23, 2015 1. Introduction the exception of leaf nodes, nodes in the trie work merely as pointers to words. Data structures are a specialized format for efficient A trie, also called digital tree, is an ordered multi- organizing, retrieving, saving and storing data. It’s way tree data structure that is useful to store an efficient with large amount of data such as: Large data associative array where the keys are usually strings, bases.
    [Show full text]
  • Data Structures and Algorithms Binary Heaps (S&W 2.4)
    Data structures and algorithms DAT038/TDA417, LP2 2019 Lecture 12, 2019-12-02 Binary heaps (S&W 2.4) Some slides by Sedgewick & Wayne Collections A collection is a data type that stores groups of items. stack Push, Pop linked list, resizing array queue Enqueue, Dequeue linked list, resizing array symbol table Put, Get, Delete BST, hash table, trie, TST set Add, ontains, Delete BST, hash table, trie, TST A priority queue is another kind of collection. “ Show me your code and conceal your data structures, and I shall continue to be mystified. Show me your data structures, and I won't usually need your code; it'll be obvious.” — Fred Brooks 2 Priority queues Collections. Can add and remove items. Stack. Add item; remove the item most recently added. Queue. Add item; remove the item least recently added. Min priority queue. Add item; remove the smallest item. Max priority queue. Add item; remove the largest item. return contents contents operation argument value size (unordered) (ordered) insert P 1 P P insert Q 2 P Q P Q insert E 3 P Q E E P Q remove max Q 2 P E E P insert X 3 P E X E P X insert A 4 P E X A A E P X insert M 5 P E X A M A E M P X remove max X 4 P E M A A E M P insert P 5 P E M A P A E M P P insert L 6 P E M A P L A E L M P P insert E 7 P E M A P L E A E E L M P P remove max P 6 E M A P L E A E E L M P A sequence of operations on a priority queue 3 Priority queue API Requirement.
    [Show full text]
  • Lecture 04 Linear Structures Sort
    Algorithmics (6EAP) MTAT.03.238 Linear structures, sorting, searching, etc Jaak Vilo 2018 Fall Jaak Vilo 1 Big-Oh notation classes Class Informal Intuition Analogy f(n) ∈ ο ( g(n) ) f is dominated by g Strictly below < f(n) ∈ O( g(n) ) Bounded from above Upper bound ≤ f(n) ∈ Θ( g(n) ) Bounded from “equal to” = above and below f(n) ∈ Ω( g(n) ) Bounded from below Lower bound ≥ f(n) ∈ ω( g(n) ) f dominates g Strictly above > Conclusions • Algorithm complexity deals with the behavior in the long-term – worst case -- typical – average case -- quite hard – best case -- bogus, cheating • In practice, long-term sometimes not necessary – E.g. for sorting 20 elements, you dont need fancy algorithms… Linear, sequential, ordered, list … Memory, disk, tape etc – is an ordered sequentially addressed media. Physical ordered list ~ array • Memory /address/ – Garbage collection • Files (character/byte list/lines in text file,…) • Disk – Disk fragmentation Linear data structures: Arrays • Array • Hashed array tree • Bidirectional map • Heightmap • Bit array • Lookup table • Bit field • Matrix • Bitboard • Parallel array • Bitmap • Sorted array • Circular buffer • Sparse array • Control table • Sparse matrix • Image • Iliffe vector • Dynamic array • Variable-length array • Gap buffer Linear data structures: Lists • Doubly linked list • Array list • Xor linked list • Linked list • Zipper • Self-organizing list • Doubly connected edge • Skip list list • Unrolled linked list • Difference list • VList Lists: Array 0 1 size MAX_SIZE-1 3 6 7 5 2 L = int[MAX_SIZE]
    [Show full text]
  • Game Trees, Quad Trees and Heaps
    CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself.
    [Show full text]
  • Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
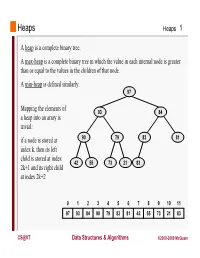
    Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { .
    [Show full text]
  • Priority Queues and Binary Heaps Chapter 6.5
    Priority Queues and Binary Heaps Chapter 6.5 1 Some animals are more equal than others • A queue is a FIFO data structure • the first element in is the first element out • which of course means the last one in is the last one out • But sometimes we want to sort of have a queue but we want to order items according to some characteristic the item has. 107 - Trees 2 Priorities • We call the ordering characteristic the priority. • When we pull something from this “queue” we always get the element with the best priority (sometimes best means lowest). • It is really common in Operating Systems to use priority to schedule when something happens. e.g. • the most important process should run before a process which isn’t so important • data off disk should be retrieved for more important processes first 107 - Trees 3 Priority Queue • A priority queue always produces the element with the best priority when queried. • You can do this in many ways • keep the list sorted • or search the list for the minimum value (if like the textbook - and Unix actually - you take the smallest value to be the best) • You should be able to estimate the Big O values for implementations like this. e.g. O(n) for choosing the minimum value of an unsorted list. • There is a clever data structure which allows all operations on a priority queue to be done in O(log n). 107 - Trees 4 Binary Heap Actually binary min heap • Shape property - a complete binary tree - all levels except the last full.
    [Show full text]
  • L11: Quadtrees CSE373, Winter 2020
    L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373,
    [Show full text]
  • CS210-Data Structures-Module-29-Binary-Heap-II
    Data Structures and Algorithms (CS210A) Lecture 29: • Building a Binary heap on 풏 elements in O(풏) time. • Applications of Binary heap : sorting • Binary trees: beyond searching and sorting 1 Recap from the last lecture 2 A complete binary tree How many leaves are there in a Complete Binary tree of size 풏 ? 풏/ퟐ 3 Building a Binary heap Problem: Given 풏 elements {푥0, …, 푥푛−1}, build a binary heap H storing them. Trivial solution: (Building the Binary heap incrementally) CreateHeap(H); For( 풊 = 0 to 풏 − ퟏ ) What is the time Insert(푥,H); complexity of this algorithm? 4 Building a Binary heap incrementally What useful inference can you draw from Top-down this Theorem ? approach The time complexity for inserting a leaf node = ?O (log 풏 ) # leaf nodes = 풏/ퟐ , Theorem: Time complexity of building a binary heap incrementally is O(풏 log 풏). 5 Building a Binary heap incrementally What useful inference can you draw from Top-down this Theorem ? approach The O(풏) time algorithm must take O(1) time for each of the 풏/ퟐ leaves. 6 Building a Binary heap incrementally Top-down approach 7 Think of alternate approach for building a binary heap In any complete 98 binaryDoes treeit suggest, how a manynew nodes approach satisfy to heapbuild propertybinary heap ? ? 14 33 all leaf 37 11 52 32 nodes 41 21 76 85 17 25 88 29 Bottom-up approach 47 75 9 57 23 heap property: “Every ? node stores value smaller than its children” We just need to ensure this property at each node.
    [Show full text]
  • Assignment of Master's Thesis
    CZECH TECHNICAL UNIVERSITY IN PRAGUE FACULTY OF INFORMATION TECHNOLOGY ASSIGNMENT OF MASTER’S THESIS Title: Approximate Pattern Matching In Sparse Multidimensional Arrays Using Machine Learning Based Methods Student: Bc. Anna Kučerová Supervisor: Ing. Luboš Krčál Study Programme: Informatics Study Branch: Knowledge Engineering Department: Department of Theoretical Computer Science Validity: Until the end of winter semester 2018/19 Instructions Sparse multidimensional arrays are a common data structure for effective storage, analysis, and visualization of scientific datasets. Approximate pattern matching and processing is essential in many scientific domains. Previous algorithms focused on deterministic filtering and aggregate matching using synopsis style indexing. However, little work has been done on application of heuristic based machine learning methods for these approximate array pattern matching tasks. Research current methods for multidimensional array pattern matching, discovery, and processing. Propose a method for array pattern matching and processing tasks utilizing machine learning methods, such as kernels, clustering, or PSO in conjunction with inverted indexing. Implement the proposed method and demonstrate its efficiency on both artificial and real world datasets. Compare the algorithm with deterministic solutions in terms of time and memory complexities and pattern occurrence miss rates. References Will be provided by the supervisor. doc. Ing. Jan Janoušek, Ph.D. prof. Ing. Pavel Tvrdík, CSc. Head of Department Dean Prague February 28, 2017 Czech Technical University in Prague Faculty of Information Technology Department of Knowledge Engineering Master’s thesis Approximate Pattern Matching In Sparse Multidimensional Arrays Using Machine Learning Based Methods Bc. Anna Kuˇcerov´a Supervisor: Ing. LuboˇsKrˇc´al 9th May 2017 Acknowledgements Main credit goes to my supervisor Ing.
    [Show full text]
  • CS 270 Algorithms
    CS 270 Algorithms Week 10 Oliver Kullmann Binary heaps Sorting Heapification Building a heap 1 Binary heaps HEAP- SORT Priority 2 Heapification queues QUICK- 3 Building a heap SORT Analysing 4 QUICK- HEAP-SORT SORT 5 Priority queues Tutorial 6 QUICK-SORT 7 Analysing QUICK-SORT 8 Tutorial CS 270 General remarks Algorithms Oliver Kullmann Binary heaps Heapification Building a heap We return to sorting, considering HEAP-SORT and HEAP- QUICK-SORT. SORT Priority queues CLRS Reading from for week 7 QUICK- SORT 1 Chapter 6, Sections 6.1 - 6.5. Analysing 2 QUICK- Chapter 7, Sections 7.1, 7.2. SORT Tutorial CS 270 Discover the properties of binary heaps Algorithms Oliver Running example Kullmann Binary heaps Heapification Building a heap HEAP- SORT Priority queues QUICK- SORT Analysing QUICK- SORT Tutorial CS 270 First property: level-completeness Algorithms Oliver Kullmann Binary heaps In week 7 we have seen binary trees: Heapification Building a 1 We said they should be as “balanced” as possible. heap 2 Perfect are the perfect binary trees. HEAP- SORT 3 Now close to perfect come the level-complete binary Priority trees: queues QUICK- 1 We can partition the nodes of a (binary) tree T into levels, SORT according to their distance from the root. Analysing 2 We have levels 0, 1,..., ht(T ). QUICK- k SORT 3 Level k has from 1 to 2 nodes. Tutorial 4 If all levels k except possibly of level ht(T ) are full (have precisely 2k nodes in them), then we call the tree level-complete. CS 270 Examples Algorithms Oliver The binary tree Kullmann 1 ❚ Binary heaps ❥❥❥❥ ❚❚❚❚ ❥❥❥❥ ❚❚❚❚ ❥❥❥❥ ❚❚❚❚ Heapification 2 ❥ 3 ❖ ❄❄ ❖❖ Building a ⑧⑧ ❄ ⑧⑧ ❖❖ heap ⑧⑧ ❄ ⑧⑧ ❖❖❖ 4 5 6 ❄ 7 ❄ HEAP- ⑧ ❄ ⑧ ❄ SORT ⑧⑧ ❄ ⑧⑧ ❄ Priority 10 13 14 15 queues QUICK- is level-complete (level-sizes are 1, 2, 4, 4), while SORT ❥ 1 ❚❚ Analysing ❥❥❥❥ ❚❚❚❚ QUICK- ❥❥❥ ❚❚❚ SORT ❥❥❥ ❚❚❚❚ 2 ❥❥ 3 ♦♦♦ ❄❄ ⑧ Tutorial ♦♦ ❄❄ ⑧⑧ ♦♦♦ ⑧ 4 ❄ 5 ❄ 6 ❄ ⑧⑧ ❄❄ ⑧ ❄ ⑧ ❄ ⑧⑧ ❄ ⑧⑧ ❄ ⑧⑧ ❄ 8 9 10 11 12 13 is not (level-sizes are 1, 2, 3, 6).
    [Show full text]
  • AVL Tree, Bayer Tree, Heap Summary of the Previous Lecture
    DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture • TREE is hierarchical (non linear) data structure • Binary trees • Definitions • Full tree, complete tree • Enumeration ( preorder, inorder, postorder ) • Binary search tree (BST) AVL tree The AVL tree (named for its inventors Adelson-Velskii and Landis published in their paper "An algorithm for the organization of information“ in 1962) should be viewed as a BST with the following additional property: - For every node, the heights of its left and right subtrees differ by at most 1. Difference of the subtrees height is named balanced factor. A node with balance factor 1, 0, or -1 is considered balanced. As long as the tree maintains this property, if the tree contains n nodes, then it has a depth of at most log2n. As a result, search for any node will cost log2n, and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost log2n, even in the worst case. AVL tree AVL tree Not AVL tree Realization of AVL tree element struct AVLnode { int data; AVLnode* left; AVLnode* right; int factor; // balance factor } Adding a new node Insert operation violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced.
    [Show full text]
  • Balanced Binary Search Trees 1 Introduction 2 BST Analysis
    csce750 — Analysis of Algorithms Fall 2020 — Lecture Notes: Balanced Binary Search Trees This document contains slides from the lecture, formatted to be suitable for printing or individ- ual reading, and with some supplemental explanations added. It is intended as a supplement to, rather than a replacement for, the lectures themselves — you should not expect the notes to be self-contained or complete on their own. 1 Introduction CLRS 12, 13 A binary search tree is a data structure that supports these operations: • INSERT(k) • SEARCH(k) • DELETE(k) Basic idea: Store one key at each node. • All keys in the left subtree of n are less than the key stored at n. • All keys in the right subtree of n are greater than the key stored at n. Search and insert are trivial. Delete is slightly trickier, but not too bad. You may notice that these operations are very similar to the opera- tions available for hash tables. However, data structures like BSTs remain important because they can be extended to efficiently sup- port other useful operations like iterating over the elements in order, and finding the largest and smallest elements. These things cannot be done efficiently in hash tables. 2 BST Analysis Each operation can be done in time O(h) on a BST of height h. Worst case: Θ(n) Aside: Does randomization help? • Answer: Sort of. If we know all of the keys at the start, and insert them in a random order, in which each of the n! permutations is equally likely, then the expected tree height is O(lg n).
    [Show full text]