Two Gettysburgians Who Led Mathematics Darren B
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Archived News
Archived News 2007-2008 News articles from 2007-2008 Table of Contents Alumnae Cited for Accomplishments and Sage Salzer ’96................................................. 17 Service................................................................. 5 Porochista Khakpour ’00.................................. 18 Laura Hercher, Human Genetics Faculty............ 7 Marylou Berg ’92 ............................................. 18 Lorayne Carbon, Director of the Early Childhood Meema Spadola ’92.......................................... 18 Center.................................................................. 7 Warren Green ................................................... 18 Hunter Kaczorowski ’07..................................... 7 Debra Winger ................................................... 19 Sara Rudner, Director of the Graduate Program in Dance .............................................................. 7 Melvin Bukiet, Writing Faculty ....................... 19 Rahm Emanuel ’81 ............................................. 8 Anita Brown, Music Faculty ............................ 19 Mikal Shapiro...................................................... 8 Sara Rudner, Dance Faculty ............................. 19 Joan Gill Blank ’49 ............................................. 8 Victoria Hofmo ’81 .......................................... 20 Wayne Sanders, Voice Faculty........................... 8 Students Arrive on Campus.............................. 21 Desi Shelton-Seck MFA ’04............................... 9 Norman -
Bryn Mawr Invite - 9/2/2011 9/2/2011 Last Completed Event
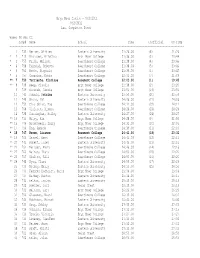
Bryn Mawr Invite - 9/2/2011 9/2/2011 Last Completed Event Women 5k Run CC Comp# Name School Time UnOfficial UO TIME =================================================================================================================== 1 732 Kerner, Whitney Eastern University 21:26.00 {8} 21:26 * 2 710 Kronauer, Kristina Bryn Mawr College 21:36.00 {3} 20:44 * 3 755 Frick, Melissa Swarthmore College 21:38.00 {4} 20:46 * 4 758 Hammond, Rebecca Swarthmore College 21:38.03 {5} 20:46 * 5 751 Beebe, Stepanie Swarthmore College 21:39.00 {6} 20:47 * 6 757 Gonzalez, Katie Swarthmore College 22:01.00 {7} 21:09 ** 7 750 Torriente, Klarisse Rosemont College 22:03.00 {1} 19:45 ** 8 708 Keep, Claudia Bryn Mawr College 22:38.00 {2} 20:20 9 709 Kosarek, Cassie Bryn Mawr College 23:51.00 {19} 23:51 10 743 Schmid, K atrina Eastern University 23:59.00 {20} 23:59 11 745 Wrona, Val Eastern University 24:06.00 {21} 24:06 12 752 Cina-Sklar, Zoe Swarthmore College 24:11.00 {22} 24:11 13 768 Violante, Ximena Swarthmore College 24:24.00 {23} 24:24 14 728 Cunningham, Hailey Eastern University 24:27.00 {24} 24:27 ** 15 716 Wiley, Kim Bryn Mawr College 24:28.00 {9} 21:59 ** 16 704 Brownawell, Emily Bryn Mawr College 24:35.00 {10} 22:06 ** 17 754 Eng, Amanda Swarthmore College 24:39.00 {11} 22:10 * 18 747 Brown, Lisanne Rosemont College 24:41.00 {18} 23:32 ** 19 766 Saarel, Emma Swarthmore College 24:41.03 {12} 22:11 ** 20 741 Rupert, Josey Eastern University 24:46.00 {13} 22:16 ** 21 761 Marquez, Mayra Swarthmore College 24:46.03 {14} 22:16 ** 22 763 Naiman, Thera Swarthmore -

The Ursinus Weekly, February 15, 1967
Ursinus College Digital Commons @ Ursinus College Ursinus Weekly Newspaper Newspapers 2-15-1967 The rsinU us Weekly, February 15, 1967 Lawrence Romane Ursinus College Herbert C. Smith Ursinus College Mort Kersey Ursinus College Frederick Jacob Ursinus College Lewis Bostic Ursinus College Follow this and additional works at: https://digitalcommons.ursinus.edu/weekly Part of the Cultural History Commons, Higher Education Commons, Liberal Studies Commons, Social History Commons, and the United States History Commons Click here to let us know how access to this document benefits oy u. Recommended Citation Romane, Lawrence; Smith, Herbert C.; Kersey, Mort; Jacob, Frederick; and Bostic, Lewis, "The rU sinus Weekly, February 15, 1967" (1967). Ursinus Weekly Newspaper. 196. https://digitalcommons.ursinus.edu/weekly/196 This Book is brought to you for free and open access by the Newspapers at Digital Commons @ Ursinus College. It has been accepted for inclusion in Ursinus Weekly Newspaper by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. .... rstnus Volume LXVI WEDNESDAY, FEBRUARY 16, 1967 Number 6 Lorelei, t he Drifters, and Winter I. F. Highlight February Social Events Winter Weekend Approaches Rock and Roll Comes to Ursinus Tomorrow evening at 8 :00 the third annual l.F.-I.s. Win On Thursday, February 16, the Agency will present the ter \Veekend will again dismember the myth of Ursinus as a DRIFTERS in concert at Ursinus. A group well known a suitcase college. In cooperation with the Agency this year mong those who enjoy rock and roll, the Drifters have been the Inter-Fraternity Inter-Sorority Council is beginning their one of America's most popular vocal groups since 1955. -

List of Members
LIST OF MEMBERS, ALFRED BAKER, M.A., Professor of Mathematics, University of Toronto, Toronto, Canada. ARTHUR LATHAM BAKER, C.E., Ph.D., Professor of Mathe matics, Stevens School, Hpboken., N. J. MARCUS BAKER, U. S. Geological Survey, Washington, D.C. JAMES MARCUS BANDY, B.A., M.A., Professor of Mathe matics and Engineering, Trinit)^ College, N. C. EDGAR WALES BASS, Professor of Mathematics, U. S. Mili tary Academy, West Point, N. Y. WOOSTER WOODRUFF BEMAN, B.A., M.A., Member of the London Mathematical Society, Professor of Mathe matics, University of Michigan, Ann Arbor, Mich. R. DANIEL BOHANNAN, B.Sc, CE., E.M., Professor of Mathematics and Astronomy, Ohio State University, Columbus, Ohio. CHARLES AUGUSTUS BORST, M.A., Assistant in Astronomy, Johns Hopkins University, Baltimore, Md. EDWARD ALBERT BOWSER, CE., LL.D., Professor of Mathe matics, Rutgers College, New Brunswick, N. J. JOHN MILTON BROOKS, B.A., Instructor in Mathematics, College of New Jersey, Princeton, N. J. ABRAM ROGERS BULLIS, B.SC, B.C.E., Macedon, Wayne Co., N. Y. WILLIAM ELWOOD BYERLY, Ph.D., Professor of Mathematics, Harvard University, Cambridge*, Mass. WILLIAM CAIN, C.E., Professor of Mathematics and Eng ineering, University of North Carolina, Chapel Hill, N. C. CHARLES HENRY CHANDLER, M.A., Professor of Mathe matics, Ripon College, Ripon, Wis. ALEXANDER SMYTH CHRISTIE, LL.M., Chief of Tidal Division, U. S. Coast and Geodetic Survey, Washington, D. C. JOHN EMORY CLARK, M.A., Professor of Mathematics, Yale University, New Haven, Conn. FRANK NELSON COLE, Ph.D., Assistant Professor of Mathe matics, University of Michigan, Ann Arbor, Mich. -

Secondary Waiver
Gettysburg College Special Waiver and Acknowledgement required for students who participate in international study, service, research and/or travel in countries for which a Travel Warning has been issued by the U.S. Department of State. The U.S. Department of State issues “Travel Warnings” when it recommends that Americans avoid a particular country or region. All Gettysburg students, regardless of nationality, who intend to participate in international study, service, research and/or travel in countries for which a Travel Warning exists prior to their departure, are required to complete this form to ensure that they are aware of the Travel Warning and its recommendations and of their personal responsibility for the risks. Gettysburg’s approval of participation is not granted unless this form is signed by the student and a parent/legal guardian. All Gettysburg students who are currently abroad when a “Travel Warning” is issued are required to complete this form and return it to Gettysburg College within 48 hours of the issuance, or their approval of participation will be rescinded. With my signature below, I acknowledge that: • I have read the attached applicable US Department of State Travel Warning issued on DATE, concerning travel by US citizens to COUNTRY. In spite of that Warning, I have voluntarily and on my own initiative elected participate in international study, service, research and/or travel in COUNTRY through Gettysburg College during TERM and I understand and accept the risks as specifically set forth in the attached travel advisory. • In addition to this document, I have also read, understood, signed, and returned the Acknowledgement of Risks form given to me by Gettysburg College. -

Classics Department Newsletter 2017-18 0
GETTYSBURG COLLEGE CLASSICS DEPARTMENT NEWSLETTER 2017-2018 blank 0 ,:: 1ij Q) Cl 0 Classics Department Newsletter 2017-18 0 Table of Contents Notes from the Department Chair …………………..... 2-3 Faculty News ……………………………………………… 3-10 Retiring! Carolyn Snively Welcome to New Faculty, Katheryn Whitcomb Prizes and Awards …………………………………………. 10-11 2017 Fall Honors Day Recipients 2017 Spring Honors Day Recipients Events and Organizations …………………........................ 11-12 2017 Spring Guest Speaker Snowball Lantern WINNER Classics Welcome Party Eta Sigma Phi Department News …………………………………………. 13-17 A Trip to Greece 2017-18 Student Staff Students Abroad Graduating Majors & Minors Connect with Classics Students Alumni News ……………………………………………… 18-21 Alumni News Send us your news 1 0 ,:: 1ij Q) Cl 0 Classics Department Newsletter 2017-18 0 From the Classics Department Chair by GailAnn Rickert Greetings from the Classics Department! Many thanks to those of you who have already written to us in response to our first Newsletter. We look forward to hearing more from you and from more of you. Our current students are eager to get to know you, and we are looking into ways that we can establish more direct and regular connections with you, either by campus visits or online meetings. If you are interested in helping us develop these ideas, please do be in touch. This year brings a big change to the Department and the College. Prof. Carolyn Snively will be graduating this spring, that is, after a long career at Gettysburg, she will be retiring at the end of this current spring semester. We will miss her. In this Newsletter please see the information about sending us your reflections and memories so that we can share them with her. -

Academic Genealogy of the Oakland University Department Of
Basilios Bessarion Mystras 1436 Guarino da Verona Johannes Argyropoulos 1408 Università di Padova 1444 Academic Genealogy of the Oakland University Vittorino da Feltre Marsilio Ficino Cristoforo Landino Università di Padova 1416 Università di Firenze 1462 Theodoros Gazes Ognibene (Omnibonus Leonicenus) Bonisoli da Lonigo Angelo Poliziano Florens Florentius Radwyn Radewyns Geert Gerardus Magnus Groote Università di Mantova 1433 Università di Mantova Università di Firenze 1477 Constantinople 1433 DepartmentThe Mathematics Genealogy Project of is a serviceMathematics of North Dakota State University and and the American Statistics Mathematical Society. Demetrios Chalcocondyles http://www.mathgenealogy.org/ Heinrich von Langenstein Gaetano da Thiene Sigismondo Polcastro Leo Outers Moses Perez Scipione Fortiguerra Rudolf Agricola Thomas von Kempen à Kempis Jacob ben Jehiel Loans Accademia Romana 1452 Université de Paris 1363, 1375 Université Catholique de Louvain 1485 Università di Firenze 1493 Università degli Studi di Ferrara 1478 Mystras 1452 Jan Standonck Johann (Johannes Kapnion) Reuchlin Johannes von Gmunden Nicoletto Vernia Pietro Roccabonella Pelope Maarten (Martinus Dorpius) van Dorp Jean Tagault François Dubois Janus Lascaris Girolamo (Hieronymus Aleander) Aleandro Matthaeus Adrianus Alexander Hegius Johannes Stöffler Collège Sainte-Barbe 1474 Universität Basel 1477 Universität Wien 1406 Università di Padova Università di Padova Université Catholique de Louvain 1504, 1515 Université de Paris 1516 Università di Padova 1472 Università -

College/University Visit Clusters
COLLEGE/UNIVERSITY VISIT CLUSTERS The groupings of colleges and universities below are by no means exhaustive; these ideas are meant to serve as good starting points when beginning a college search. Happy travels! BOSTON/RHODE ISLAND AREA Large: Boston University University of Massachusetts at Boston Northeastern University Medium: Bentley University (business focus) Boston College Brandeis University Brown University Bryant College (business focus) Harvard University Massachusetts Institute of Technology Providence College University of Massachusetts at Lowell University of Rhode Island Suffolk University Small: Babson College (business focus) Emerson College Olin College Rhode Island School of Design (art school) Salve Regina University Simmons College (all women) Tufts University Wellesley College (all women) Wheaton College CENTRAL/WESTERN MASSACHUSETTS Large: University of Massachusetts at Amherst/Lowell Medium: College of the Holy Cross Worcester Polytechnic Institute Small: Amherst College Clark University Hampshire College Mount Holyoke College (all women) Smith College (all women) Westfield State University Williams College CONNECTICUT Large: University of Connecticut Medium: Fairfield University Quinnipiac University Yale University Small: Connecticut College Trinity College Wesleyan University NORTHERN NEW ENGLAND Large: University of New Hampshire University of Vermont Medium: Dartmouth College Middlebury College Small: Bates College Bennington College Bowdoin College Colby College College of the Atlantic Saint Anselm College -

Historical Memory Symposium | June 2-5, 2019 Gettysburg College
! Historical Memory Symposium | June 2-5, 2019 Gettysburg College | Gettysburg, Pennsylvania, USA Sunday, June 2nd 6 pm Welcome dinner at the Gettysburg Hotel Monday, June 3rd 9 am Opening Remarks & Introductions | All seminars held in Science Center 200 9:30-10:30 am Monumental Commemorations Julian Bonder, architect; Roger Williams College Exploring the role of monuments, parks and museums in preserving and celebrating historic events and in shaping collective memory 11 am-3 pm Guided Visit to Gettysburg Battlefield Led by Peter Carmichael and Jill Titus, Civil War Institute at Gettysburg College 3 pm-5:30 pm Gettysburg Museum and Visitors’ Center Tuesday, June 4th 9-10:15 am Memory vis-à-vis Recent Events in the United States and Central America Stephen Kinzer, Watson Institute for International and Public Affairs, Brown University Location: Science Center 200 10:30-11:45 am Historical Memory Research I: SPAIN Brief presentations by faculty and students about their research focused on historical and collective memory, with a focus on methodologies. Juanjo Romero, Resident Director, CASA Barcelona Ava Rosenberg, Returning student, CASA Spain Maria Luisa Guardiola, Professor, Swarthmore 12-1 pm Lunch 1:15-2:15 pm Historical Memory Research II: CUBA Brief presentations by faculty and students about their research focused on historical and collective memory, with a focus on methodologies. Somi Jun, Returning student, CASA Cuba Rainer Schultz, Resident Director, CASA Cuba 2:30-4 pm De-Brief and Sharing Project Ideas 5:30-7:30 pm Dinner and closing remarks | Atrium Dining Hall Speaker Bios Julian Bonder Professor of Architecture, Roger Williams University Julian Bonder is a teacher, designer and architect born in New York and raised in Argentina. -

Elite Colleges Or Colleges for the Elite?: a Qualitative Analysis of Dickinson Students' Perceptions of Privilege Margaret Lee O'brien Dickinson College
Dickinson College Dickinson Scholar Student Honors Theses By Year Student Honors Theses 5-22-2011 Elite Colleges or Colleges For the Elite?: A Qualitative Analysis of Dickinson Students' Perceptions of Privilege Margaret Lee O'Brien Dickinson College Follow this and additional works at: http://scholar.dickinson.edu/student_honors Part of the Sociology Commons Recommended Citation O'Brien, Margaret Lee, "Elite Colleges or Colleges For the Elite?: A Qualitative Analysis of Dickinson Students' Perceptions of Privilege" (2011). Dickinson College Honors Theses. Paper 129. This Honors Thesis is brought to you for free and open access by Dickinson Scholar. It has been accepted for inclusion by an authorized administrator. For more information, please contact [email protected]. Elite Colleges or Colleges for the Elite?: A Qualitative Analysis of Dickinson Students' Perceptions of Privilege By Margaret O'Brien Submitted in partial fulfillment of Honors Requirements For the Dickinson College Department of Sociology Professor Steinbugler, Advisor Professor Schubert, Reader Professor Love, Reader 16 May 2011 Table of Contents 1. Introduction ~----------------------~2 2. Literature Review 4 3. Methodology 20 4. Data Analysis 29 5. Conclusion 48 6. Acknowledgements 52 7. Appendix A (Interview Recruitment Flier) 53 8. Appendix B (Interview Recruitment Email) 54 9. References 55 1 Studying privileged people is important because they create the ladders that others must climb to move up in the world. Nowhere is this more true than in schools, which have been official ladders of mobility and opportunity in U.S. society for hundreds of years. Mitchell L. Stevens, Creating a Class The college experience is often portrayed as a carefree four years filled with new experiences, lifelong friendships, parties, papers and the ease of a semi-sheltered, yet independent, life. -

The Classicists of Ohio Wesleyan University: 1844-2014 © Donald Lateiner 2014
The Classicists of Ohio Wesleyan University: 1844-2014 © Donald Lateiner 2014 When Ohio Wesleyan could hire only four professors to teach in Elliott Hall (and there was yet no other building), one of the four professors taught Latin and another taught Ancient Greek. This I was told in 1979, when I arrived at Sturges Hall to teach the Classics. True or not,1 the story reflects the place of Greek and Latin in the curriculum of the mid-1800s. Our first graduate, William Godman, followed the brutally demanding “classical course.” The percentage of faculty teaching Greek and Latin steadily declined in the Nineteenth and most of the Twentieth century. New subjects and new demands attracted Wesleyan students. Currently we descry another Renaissance of antiquity at Ohio Wesleyan in Classical Studies. Sturges Hall itself was opened in 1855, its original function, as you see in the photo on the left, to serve the campus as library with alcoves divided by subject. Thomas Jefferson and John Quincy Adams studied and revered Greek and Roman writers, their demanding languages, and their culture. Ben Franklin was not interested. For many decades, mere admission to Harvard College required a solid knowledge of Greek and Latin. One of Ohio’s sons who became President of the United States, James A. Garfield, was both a student and a teacher of Greek and Latin. Legend holds that he could write Greek with one hand, Latin with the other--at the same time. I doubt it, but Thucydides tells us humans usually doubt that others can achieve what they know they cannot. -

2019-20 Fact Book
Gettysburg College Fact Book 2019–20 Office of Institutional Analysis Gettysburg College • Office of Institutional Analysis Fact Book 2019–20 Table of Contents General Information 19 Campus Racial/Ethnic Diversity: Students and Employees Preface (Full-Time Only) 1 College Organizational Chart 20 Racial/Ethnic Affiliations 2 College Committees of College Personnel 3 Faculty Councils and Committees Admissions, First-Year 4 Committees of the Board of Trustees Students, and Financial Aid 5 Profile and Historical Overview 21 Applications, Accepted, 7 Facts in Brief / Quick Facts and Enrolled 22 Admissions 10-Year Trends Academic Program/ Curricular Information 23 Geographical Distribution of First-Year Students 9 Degrees Awarded by Major 24 Growth in International 10 Minors Granted by Department and Domestic Diversity 11 Teacher Certification of the First-Year Class 25 Anticipated Majors of High-Impact Practices First-Year Students 12 Participation in Select High-Impact 27 First-Generation Students Learning Experiences in the First-Year Cohort Faculty and Staff 28 Pell Grant Recipients in the First-Year Cohort 13 Class Sessions by Department 29 Financial Aid Summary Data (Fall 2018) 15 Class Sessions by Department Enrollment (Spring 2019) 30 Enrollment by Semester 16 Full-Time Faculty by Gender, and Gender Degree, Rank, and Length 31 Enrollment by Class and Gender of Service 32 Fall Enrollment 10-Year 17 Full-Time Faculty Profile Trends: Total, On-Campus, Historical Trends and Off-Campus 18 Growth in International and Domestic Diversity of