University of Huddersfield Repository
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TV Nr. Name Frequ. Pol. Symbolr. FEC Sat Label Ch. ID Vpid Apid
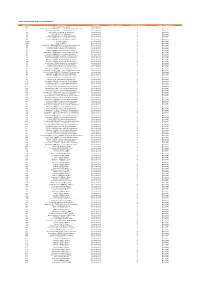
TV Nr. Name Frequ. Pol. Symbolr. FEC Sat Label Ch. ID Vpid Apid PCR Pid 1 OTA 11038 hor 40700 auto 0936 0936 225 0 0 0 2 OTA 12534 vert 40700 auto 0936 0936 225 0 0 0 3 OTA 12595 vert 40700 auto 0936 0936 225 0 0 0 4 OTA 12647 hor 27500 auto 0936 0936 225 0 0 0 5 DISH TRIVIA 12688 vert 27500 auto 0936 0936 246 0 0 0 6 EURO 12688 vert 27500 auto 0936 0936 230 0 0 0 7 iGUIDE 12688 vert 27500 auto 0936 0936 232 0 0 0 8 MINIKIDS 12688 vert 27500 auto 0936 0936 245 0 0 0 9 TEST1 12688 vert 27500 auto 0936 0936 244 0 0 0 10 TEST2 12688 vert 27500 auto 0936 0936 242 0 0 0 11 DD BANGLA 10990 vert 27500 auto 0936 0936 1060 506 606 506 12 DD BHARATI 10990 vert 27500 auto 0936 0936 1050 505 605 505 13 DD-CHANDANA 10990 vert 27500 auto 0936 0936 1070 507 607 507 14 DD GUJARATI 10990 vert 27500 auto 0936 0936 1080 508 608 708 15 DD INDIA 10990 vert 27500 auto 0936 0936 1040 504 604 704 16 DD KASHIR 10990 vert 27500 auto 0936 0936 1090 509 609 709 17 DD NATIONAL 10990 vert 27500 auto 0936 0936 1010 501 601 701 18 DD NEWS 10990 vert 27500 auto 0936 0936 1020 502 602 702 19 DD SPORTS 10990 vert 27500 auto 0936 0936 1030 503 603 703 20 LOK SABHA TV 10990 vert 27500 auto 0936 0936 1110 511 611 511 21 LIVE INDIA 11038 hor 40700 auto 0936 0936 30013 2911 2912 2911 22 DD MALAYALAM 11070 vert 27500 auto 0936 0936 1270 527 627 727 23 DD NORTH EAST 11070 vert 27500 auto 0936 0936 1210 521 621 721 24 DD ORIYA 11070 vert 27500 auto 0936 0936 1220 522 622 522 25 DD PODHIGAI 11070 vert 27500 auto 0936 0936 1230 523 623 523 26 DD PUNJABI 11070 vert 27500 auto 0936 -

Republic of Ireland. Wikipedia. Last Modified
Republic of Ireland - Wikipedia, the free encyclopedia What links here Related changes Upload file Special pages Republic of Ireland Permanent link From Wikipedia, the free encyclopedia Page information Data item This article is about the modern state. For the revolutionary republic of 1919–1922, see Irish Cite this page Republic. For other uses, see Ireland (disambiguation). Print/export Ireland (/ˈaɪərlənd/ or /ˈɑrlənd/; Irish: Éire, Ireland[a] pronounced [ˈeː.ɾʲə] ( listen)), also known as the Republic Create a book Éire of Ireland (Irish: Poblacht na hÉireann), is a sovereign Download as PDF state in Europe occupying about five-sixths of the island Printable version of Ireland. The capital is Dublin, located in the eastern part of the island. The state shares its only land border Languages with Northern Ireland, one of the constituent countries of Acèh the United Kingdom. It is otherwise surrounded by the Адыгэбзэ Atlantic Ocean, with the Celtic Sea to the south, Saint Flag Coat of arms George's Channel to the south east, and the Irish Sea to Afrikaans [10] Anthem: "Amhrán na bhFiann" Alemannisch the east. It is a unitary, parliamentary republic with an elected president serving as head of state. The head "The Soldiers' Song" Sorry, your browser either has JavaScript of government, the Taoiseach, is nominated by the lower Ænglisc disabled or does not have any supported house of parliament, Dáil Éireann. player. You can download the clip or download a Aragonés The modern Irish state gained effective independence player to play the clip in your browser. from the United Kingdom—as the Irish Free State—in Armãneashce 1922 following the Irish War of Independence, which Arpetan resulted in the Anglo-Irish Treaty. -

Scheduling As a Tool of Management in RTÉ Television
Technological University Dublin ARROW@TU Dublin Doctoral Applied Arts 2011-7 Rationalising Public Service: Scheduling as a Tool of Management in RTÉ Television Ann-Marie Murray Technological University Dublin, [email protected] Follow this and additional works at: https://arrow.tudublin.ie/appadoc Part of the Arts Management Commons, Business and Corporate Communications Commons, and the Other Film and Media Studies Commons Recommended Citation Murray, A. (2011) Rationalising Public Service: Scheduling as a Tool of Management in RTÉ Television. Doctoral Thesis, Technological University Dublin. doi:10.21427/D70307 This Theses, Ph.D is brought to you for free and open access by the Applied Arts at ARROW@TU Dublin. It has been accepted for inclusion in Doctoral by an authorized administrator of ARROW@TU Dublin. For more information, please contact [email protected], [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License Rationalising Public Service: Scheduling as a Tool of Management in RTÉ Television Ann-Marie Murray This thesis is submitted to the Dublin Institute of Technology in Candidature for the Degree of Doctor of Philosophy July 2011 School of Media Faculty of Applied Arts Supervisor: Dr. Edward Brennan Abstract Developments in the media industry, notably the increasing commercialisation of broadcasting and deregulation, have combined to create a television system that is now driven primarily by ratings. Public broadcast organisations must adopt novel strategies to survive and compete in this new environment, where they need to combine public service with popularity. In this context, scheduling has emerged as the central management tool, organising production and controlling budgets, and is now the driving force in television. -
Codes Used in D&M
CODES USED IN D&M - MCPS A DISTRIBUTIONS D&M Code D&M Name Category Further details Source Type Code Source Type Name Z98 UK/Ireland Commercial International 2 20 South African (SAMRO) General & Broadcasting (TV only) International 3 Overseas 21 Australian (APRA) General & Broadcasting International 3 Overseas 36 USA (BMI) General & Broadcasting International 3 Overseas 38 USA (SESAC) Broadcasting International 3 Overseas 39 USA (ASCAP) General & Broadcasting International 3 Overseas 47 Japanese (JASRAC) General & Broadcasting International 3 Overseas 48 Israeli (ACUM) General & Broadcasting International 3 Overseas 048M Norway (NCB) International 3 Overseas 049M Algeria (ONDA) International 3 Overseas 58 Bulgarian (MUSICAUTOR) General & Broadcasting International 3 Overseas 62 Russian (RAO) General & Broadcasting International 3 Overseas 74 Austrian (AKM) General & Broadcasting International 3 Overseas 75 Belgian (SABAM) General & Broadcasting International 3 Overseas 79 Hungarian (ARTISJUS) General & Broadcasting International 3 Overseas 80 Danish (KODA) General & Broadcasting International 3 Overseas 81 Netherlands (BUMA) General & Broadcasting International 3 Overseas 83 Finnish (TEOSTO) General & Broadcasting International 3 Overseas 84 French (SACEM) General & Broadcasting International 3 Overseas 85 German (GEMA) General & Broadcasting International 3 Overseas 86 Hong Kong (CASH) General & Broadcasting International 3 Overseas 87 Italian (SIAE) General & Broadcasting International 3 Overseas 88 Mexican (SACM) General & Broadcasting -

DOCUMENT RESUME Proceedings of the Annual Meeting of The
DOCUMENT RESUME ED 423 574 CS 509 918 TITLE Proceedings of the Annual Meeting of the Association for Education in Journalism and Mass Communication (81st, Baltimore, Maryland, August 5-8, 1998). Radio-TV. INSTITUTION Association for Education in Journalism and Mass Communication. PUB DATE 1998-08-00 NOTE 362p.; For other sections of these Proceedings, see CS 509 905-922. PUB TYPE Collected Works Proceedings (021) Reports Research (143) EDRS PRICE MF01/PC15 Plus Postage. DESCRIPTORS *Broadcast Journalism; Case Studies; Content Analysis; Females; Foreign Countries; Higher Education; National Surveys; *News Media; Political Campaigns; *Radio; Student Attitudes; *Television; Television Research IDENTIFIERS China; Local Television Stations; *Media Coverage; *Television News ABSTRACT The Radio-TV section of the Proceedings contains the following 13 papers: "Computer-Assisted Reporting: A Nationwide Survey of Television Newsrooms" (Sonya Forte Duhe' and Erin Haynie); "Network Television News Coverage of the Environment and the Impact of the Electronic Newsletter 'Greenwire" (Claudette Guzan Artwick); "Managing Single-Market Radio Clusters" (Greg Stefaniak); "A Content Analysis of 'Dateline NBC' and 'NBC Nightly News': The Infiltration of the Youformation Story into News Magazines and Mainstream News" (Jeff Demas); "Priming Reporters: A Study on How the Willie Horton Case Altered the Portrayal of Criminals" (James Devitt); "Constructing International Spectacle on Television: CCTV News and China's Window on the World, 1992-1996" (Tsan-Kuo Chang and Chen Yanru); "Advertising's Influence on Broadcast News Content: A Study of Student Attitudes" (Hubert W. Brown and Beth E. Barnes); "Women in Television News Management: Do They Make a Difference?" (Laura K. Smith and John W. Wright II); "They'd Rather Be in Pictures, or Would They?: A Content Analysis of Video Bite Bias during TV Network News Coverage of the 1992 and 1996 Presidential Campaigns" (Jon A. -

Broadcast Bulletin Issue Number
O fcom Broadcast Bulletin Issue number 100 14 January 2008 Ofcom Broadcast Bulletin, Issue 100 14 January 2008 Contents Introduction 3 Standards cases In Breach McFly Competition 4 BBC North West Tonight (BBC1), 6, 8, and 9 February 2007 Dirty Cows 6 LIVING, 14 October 2007, 17:00 UK’s Toughest Jobs 7 Discovery+1, 20 October 2007, 16:00 Rich Kids’ Cattle Drive 8 E! Entertainment, 29 October 2007, 17:20 Ryanair.com POP POP POP 9 Bubble Hits, 9 November 2007, 14:00 Radio Ramadan (Bristol) 10 11 and 12 October 2007, various times Resolved F1: Japanese Grand Prix 11 ITV1, 30 September 2007, 04:30 Not in Breach Hell’s Kitchen 12 ITV1: 4, 6, 7, 8 and 10 September 2007, various times Weekend “Nazis” 15 BBC1, 27 August 2007, 20:30 Crash Test Dummies 17 Sky One, 7 October 2007, 09:00 Fairness & Privacy cases Partly Upheld Complaint by Brodies LLP Solicitors on behalf of Parks of Hamilton 19 (Coach Hirers) Limited News Items, Real Radio (Central Scotland), 5 January 2007 Other programmes not in breach/outside remit 22 2 Ofcom Broadcast Bulletin, Issue 100 14 January 2008 Introduction Ofcom’s Broadcasting Code (“the Code”) took effect on 25 July 2005 (with the exception of Rule 10.17 which came into effect on 1 July 2005). This Code is used to assess the compliance of all programmes broadcast on or after 25 July 2005. The Broadcasting Code can be found at http://www.ofcom.org.uk/tv/ifi/codes/bcode/ The Rules on the Amount and Distribution of Advertising (RADA) apply to advertising issues within Ofcom’s remit from 25 July 2005. -

IMRO Annual Report 2007
IMRO ANNUAL REPORT & ACCOUNTS 2007 Cover IMRO.indd 1 07/08/2008 10:50:57 IMRO ANNUAL REPORT & ACCOUNTS 2007 Title Page IMRO 1 30/07/2008 1 3:11:55 Blank Page IMRO 1 30/07/2008 1 3:07:51 IMRO BOARD OF DIRECTORS: Keith Donald (Cathaoirleach), Paul Brady, Philip Flynn, Eddie Joyce, Johnny Lappin, Steve Lindsey (UK), Donagh Long, Eleanor McEvoy, Charlie McGettigan, Christy Moore, James Morris, CREDITS Michael O’Riordan, Niall Toner. PRODUCTION MANAGER: Mairin Sheehy CONTRIBUTORS: Jackie Hayden, Greg McAteer, Colm O’Hare, Peter Murphy DESIGN & PRODUCTION: Hot Press, 13 Trinity Street, Dublin 2. ART DIRECTOR: David Keane ADDITIONAL DESIGN: Graham Keogh PRODUCTION CO-ORDINATOR: Anne Marie Conlon 3 Credits IMRO 1 30/07/2008 1 3:13:14 Blank Page IMRO 1 30/07/2008 1 3:08:22 6 TAKING IMRO TO HEART KEITH DONALD tells us about his plans for his term as IMRO Chairman. 9 FINANCIAL HIGHLIGHTS IN 2007 10 IMRO WELCOMES NEW CEO VICTOR FINN We talk to newly-appointed CEO, VICTOR FINN about the future of the CONTENTS organisation. 12 NEWS REVIEW A look at the music news that made headlines over the last year. 15 IMRO MOVING AHEAD Publishers MICHAEL O’RIORDAN, PETER BARDON and STEVE LINDSEY share their views on the challenges and opportunities facing Irish music. 18 THE SONGWRITERS’ PERSPECTIVE PAUL BRADY and ELEANOR MCEVOY on the trials and tribulations of being a modern-day songwriter. 20 ONCE UPON A TIME GLEN HANSARD and MARKETA IRGLOVA talk about the life-changing experience of winning an Oscar in March 2008. -

Mediaworks-Outlook-17.Pdf
+ + 01001111 01010101 01010100 + 00110010 00110000 00110001 + 00110110 01001100 00001010 01001111 + 01001111 01001011 + CONTENTS AN INTRODUCTION .......................................................................................2 THE CONSUMER ............................................................................................4 IS A DATA ................................................................................................................6 FORCE ONLINE ...........................................................................................................8 DISPLAY ......................................................................................................9 SEARCH ....................................................................................................10 SOCIAL ......................................................................................................11 VIDEO ............................................................................................................12 NEWS MEDIA ..............................................................................................14 RADIO ...........................................................................................................16 OUT OF HOME ..............................................................................................18 SPONSORSHIP .............................................................................................20 DIRECT MARKETING ....................................................................................22 -
Tvbox Channel List
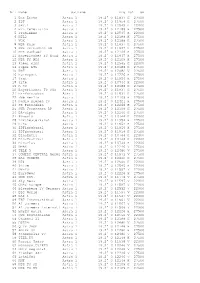
Nr. Name Satname Frq Pol SR 1 Das Erste Astra 1 19.2° O 11837 H 27500 2 ZDF Astra 1 19.2° O 11954 H 27500 3 SAT.1 Astra 1 19.2° O 12545 H 22000 4 RTL Television Astra 1 19.2° O 12188 H 27500 5 ProSieben Astra 1 19.2° O 12545 H 22000 6 RTL2 Astra 1 19.2° O 12188 H 27500 7 VOX Astra 1 19.2° O 12188 H 27500 8 WDR Köln Astra 1 19.2° O 11837 H 27500 9 SWR Fernsehen BW Astra 1 19.2° O 11837 H 27500 10 MDR Sachsen Astra 1 19.2° O 12109 H 27500 11 Bayerisches FS Nord Astra 1 19.2° O 11837 H 27500 12 NDR FS NDS Astra 1 19.2° O 12109 H 27500 13 kabel eins Astra 1 19.2° O 12545 H 22000 14 Super RTL Astra 1 19.2° O 12188 H 27500 15 DSF Astra 1 19.2° O 12480 V 27500 16 Eurosport Astra 1 19.2° O 12226 H 27500 17 3sat Astra 1 19.2° O 11954 H 27500 18 arte Astra 1 19.2° O 10744 H 22000 19 n-tv Astra 1 19.2° O 12188 H 27500 20 Bayerisches FS Süd Astra 1 19.2° O 11837 H 27500 21 hr-fernsehen Astra 1 19.2° O 11837 H 27500 22 rbb Berlin Astra 1 19.2° O 12109 H 27500 23 Radio Bremen TV Astra 1 19.2° O 12421 H 27500 24 SR Fernsehen Astra 1 19.2° O 12266 H 27500 25 SWR Fernsehen RP Astra 1 19.2° O 12109 H 27500 26 BR-alpha Astra 1 19.2° O 12266 H 27500 27 Phoenix Astra 1 19.2° O 10744 H 22000 28 ZDFtheaterkanal Astra 1 19.2° O 11954 H 27500 29 KiKa Astra 1 19.2° O 11954 H 27500 30 ZDFinfokanal Astra 1 19.2° O 11954 H 27500 31 ZDFdokukanal Astra 1 19.2° O 11954 H 27500 32 EinsExtra Astra 1 19.2° O 10744 H 22000 33 EinsFestival Astra 1 19.2° O 10744 H 22000 34 EinsPlus Astra 1 19.2° O 10744 H 22000 35 DMAX Astra 1 19.2° O 12246 V 27500 36 TELE 5 Astra 1 19.2° O 12480 V 27500 37 COMEDY CENTRAL Germa Astra 1 19.2° O 11973 V 27500 38 DAS VIERTE Astra 1 19.2° O 12460 H 27500 39 N24 Astra 1 19.2° O 12545 H 22000 40 9Live Astra 1 19.2° O 12545 H 22000 41 DW-TV Astra 1 19.2° O 11597 V 22000 42 EuroNews Astra 1 19.2° O 12226 H 27500 43 CNN Int. -

December 2008 259 Malaysia Film January
UDC Usage Description Period 159 Croatia GB January ‐ December 2008 259 Malaysia Film January ‐ December 2008 127 Malaysia GB January ‐ December 2008 332 Malaysia Online January ‐ December 2008 116 Canada Film January ‐ March 2009 115 Canada GB January ‐ March 2009 123 Poland GB January ‐ June 2009 124 Poland Film January ‐ June 2009 323 Poland Online January ‐ November 2009 096 Greece GB September 2008 ‐ February 2009 066 Greece Film September 2008 ‐ February 2009 333 Greece Online September 2008 ‐ February 2009 141 Slovakia GB January ‐ December 2008 138 Peru GB January 2000 ‐ December 2006 122 Hungary Film January ‐ December 2008 079 Hungary GB January ‐ December 2008 248 Singapore Film July ‐ December 2008 128 Singapore GB July ‐ December 2008 098 Mexico Film April ‐ June 2009 88 Mexico GB April ‐ June 2009 148 Brazil Film April ‐ June 2009 147 Brazil GB April ‐ June 2009 063 Spain Film January ‐ June 2009 093 Spain GB January ‐ June 2009 271 Spain Live July ‐ September 2009 314 Spain Online July ‐ September 2009 272 Spain Symphonic January ‐ June 2009 074 Austria GB January ‐ December 2008 044 Austria Film January ‐ December 2008 064 Sweden Film January ‐ June 2009 094 Sweden GB January ‐ June 2009 319 Sweden Online July 2006 ‐ June 2009 080 Denmark GB January ‐ December 2008 318 Denmark Online January 2008 ‐ June 2009 059 Norway Film January ‐ December 2008 089 Norway GB January ‐ December 2008 051 Holland Film January ‐ December 2008 081 Holland GB January ‐ December 2008 308 Holland Online January ‐ December 2008 129 Australia -
Wayne Township Public Library, Final Performance Report for Library Services and Construction Act (LSCA) Title VI, Library Literacy Program
DOCUMENT RESUME ED 416 889 IR 056 914 AUTHOR Smyth, Carol B.; Grannell, Dorothy S.; Moore, Miriam TITLE Wayne Township Public Library, Final Performance Report for Library Services and Construction Act (LSCA) Title VI, Library Literacy Program. INSTITUTION Wayne Township Public Library, Richmond, IN. SPONS AGENCY Office of Educational Research and Improvement (ED), Washington, DC. Office of Library Programs. PUB DATE 1994-00-00 NOTE 352p.; Wayne Township Public Library is also known as Morrisson-Reeves Library. CONTRACT RI67A327 PUB TYPE Numerical/Quantitative Data (110) Reports - Descriptive (141) EDRS PRICE MF01/PC15 Plus Postage. DESCRIPTORS *Adult Basic Education; *Adult Learning; *Adult Literacy; Community Cooperation; English (Second Language); Family Literacy; Federal Programs; Grants; Homeless People; Intergenerational Programs; Learning Disabilities; Library Collection Development; Library Role; *Literacy Education; Microcomputers; Older Adults; Public Libraries; Publicity; Student Recruitment; Tutoring; Tutors; Volunteer Training; Volunteers; Workplace Literacy IDENTIFIEPS Library Services and Construction Act; Tutor Training; Volunteer Recruitment ABSTRACT The Literacy Resource Center project, a program of the Wayne Township Public Library also known as the Morrisson-Reeves Library (Richmond, Indiana), involved recruitment, retention, coalition building, public awareness, training, basic literacy, collection development, tutoring, computer-assisted, other technology, employment oriented, intergenerational/family, and English as a Second Language (ESL) programs. The project served a community of 50,000-100,000 people and targeted the homeless, learning disabled, workforce/workplace learners, seniors/older citizens, intergenerational/families, and ESL learners. Tutoring was done one-on-one, in small groups, and in classes, using the Laubach, Literacy Volunteers of America (LVA), Orton-Gillingham, and Steck-Vaughn methods. The project served 211 adult learners, and provided 3,710 hours of direct tutoring service. -

Sky Price Matrix2007-8
Email: [email protected] Phone: 089/90539376 Last update 16.09.07 Package 1A (Sky World) (£45/€67.50/$91.50) Package 1B (Sky Movie World) (£38/€57/$77.50) Package 1C (Sky Sports World) (£38/€57/$77.50) Package 01 (Sky Family Pack) (£21/€31.50/$43) For SKY HD channels and services add £10/€15/$21 per month to all the above package prices Included in all packages: Email: [email protected] Phone: 089/90539376 Last update 16.09.07 Family Pack (Package 01) contains the following channels (status 01.09.2007): Variety Discovery Home & Non-Subscription Chart Show TV Bangla TV Sky One Health +1 BBC ONE Classic FM TV Golf Pro-Shop Sky Two BBC TWO channel U Get Lucky TV Sky Three Knowledge BBC THREE CCTV9 Vegas 24/7 Sky Vegas Live National Geo. + 1 BBC FOUR POP B4U Music TCM Nat Geo Wild BBC HD CBBC BIG GAME TV! TCM 2 UKTV History ITV1 CBeebies Bliss UK Drama Adventure One ITV2 QVC MusFlash TV UK TV Gold Animal Planet ITV2 +1 TV Shop ROCKWORLD TV UK TV Gold +1 Animal Planet + 1 ITV3 Gems TV Zee Music UKTV G2 Bio ITV3 +1 Gems TV2 Bonanza UKTV G2+1 Discovery Channel ITV4 Ideal World Bubble Hits LIVINGtv Discovery + 1hr CITV Star Bazaar TV Channel M LIVING+1 Discovery Civilisation ITV Play U save .TV Channel Punjab LIVING2 Discovery Science Sky News Shop Vector Channel ‘S’ E4 Discovery Turbo Sky Three Shop Vector + Channel ‘S’ ATN E4 +1 National Geographic Channel 4 Vector 24/7 Channel ‘S’ NTV FX The History Channel Five Price Drop TV Chat Box FX+ History + 1 hr Five Life Best Direct DAYSTAR Ftn UKTV Documentary Five US Price Crash