DOCSLIB.ORG

Electromagnetic Radiation (EMR) Basics for Remote Sensing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Electromagnetic Radiation (EMR) Basics for Remote Sensing -1- Electromagnetic radiation (EMR) basics for remote sensing HANDOUT’s OBJECTIVES: • familiarize student with basic EMR terminology & mathematics • overview of EMR polarization as related to remote sensing • introduce ray/wave/particle descriptions of EMR • introduce geometrical & spectral classification of EMR • some practical remote-sensing applications of EMR fundamentals What do we mean by EMR? propagation through space of a time-varying wave that has both electrical and magnetic components Consider a simple sine wave as our model, with: wavelength ≡ λ (“lambda”), frequency ≡ ν (“nu”), and speed V = νλ 1 The wave’s period T = ν . In a vacuum, the speed is denoted as c (c ≈ 3 x 108 m/sec). wavelength λ crest wave amplitude E 0 trough c The real index of refraction n is defined by n = V . Ν.Β.: the speed referred to here is that of the waveform, not of any object, so that values of n < 1 (and thus V > c) are possible. SO431 — EMR basics for remote sensing (8-21-09) -2- How do we describe this EMR wave? arrow = propagation direction x Light consists of oscillating electrical fields (denoted E above), and magnetic fields (denoted B). We’ll concentrate on E and ignore B, however, we could just as easily describe light using B. We don’t do it because the interaction of magnetic fields with charged particles is more complex than electric fields, but we could. SO431 — EMR basics for remote sensing (8-21-09) -3- Light whose electric field oscillates in a particular way is called polarized. If the oscillation lies in a plane, the light is called plane or linearly polarized (top right). Linearly polarized light can be polarized in different directions (e.g., vertical or horizontal above). Light can also be circularly polarized, with its electric field direction spiraling in a screw pattern or helix that has either a right- or left-handed sense (bottom). Seen along propagation axis x this helix has a circular cross-section. Light can also combine linear and circular polarization — its electric field then traces out a helix with an elliptical cross-section. Such light is called elliptically polarized. We often speak of unpolarized light, yet each individual EMR wave is itself completely polarized. Unpolarized light is actually the sum of light emitted by many different charges that accelerate in random directions. Real detectors like radiometers can only observe the space- and time-averaged intensities of the myriad oscillating charges. If this light has an observable dominant polarization, we call it polarized. Polarized light in remote-sensing applications 1 1 P(θ) ⊥-polarized radiance 0.8 | |-polarized radiance 0.8 P at θ = 53° max 0.6 0.6 θ) P( 0.4 polarization by reflection 0.4 by water (n = 4/3) reflected 0.2 0.2 0 0 0° 10° 20° 30° 40° 50° 60° 70° 80° 90° incidence angle (θ) Most environmental light sources such as sunlight are unpolarized. Thus passive remote-sensing systems usually don’t benefit from the extra information that a polarized light source provides. Radar and other active remote-sensing systems usually emit SO431 — EMR basics for remote sensing (8-21-09) -4- polarized EMR, and so they can exploit the different signal patterns reflected when different polarizations illuminate the surface. Yet even reflected sunlight can be polarized, as the graph above indicates. It shows how polarization varies with incidence angle θ (incident EMR’s angle with the surface normal) for unpolarized light reflected by a smooth water surface. Degree of polarization P varies from 0 (completely unpolarized reflected light) to 1 (completely polarized reflection). In fact, the graph explains an entire industry — manufacture of polarizing sunglasses. observer’s eye u ) n lly po ia d la rt te r a ec iz (p fl ed re i d nc ze id ri en la t po smooth, non-metallic surface Like all linear polarizers, the plastic sheet polarizers used in some sunglasses have a particular direction along which linearly polarized light is absorbed least; polarized light is absorbed more strongly in other directions. This minimum-absorption direction is called the polarizer’s transmission axis. When linearly polarized light’s oscillation direction parallels the polarizer transmission axis, we get maximum transmission. Rotate the light source 90˚ about its propagation axis (or rotate the filter 90˚ about that axis), and we get minimum transmission. • At what θ is there maximum polarization for reflection by water? • How does the P(θ) graph help explain the changing effectiveness of polarizing sunglasses? • To be most effective in reducing reflected glare, should the sunglasses’ transmission axis be oriented horizontal, diagonal, or vertical to the water surface? (Hint: Examine the drawing above to see the oscillation direction of the reflected, partially polarized light.) Now return to our explanation of EMR’s wave nature. Mathematically, the wave amplitude E is given by, at any time t and position x (with x measured along the direction of propagation): t x π[ - (Eq. 1). E = Eo sin(2 T λ]) SO431 — EMR basics for remote sensing (8-21-09) -5- By setting t, x to fixed values in Eq. 1, we can determine the electromagnetic wave’s propagation direction. In addition, we can use Fourier analysis to reduce any waveform, no matter how complicated, to a sum of simple sine and cosine waves. This has mathematical advantages when we try to analyze the wave’s physical significance and sources. Note that Eq. 1 can be rewritten as: π 2 → E = Eo sin( λ [ct - x]) πν → E = Eo sin(2 [t - x/c]) (factor out c from the [ ], and note that c/λ = ν) ω − δ E = Eo sin( t ), where ω = 2πν = 2π/T and δ = 2πx/λ. Note that ω is described as the rotational angular frequency (in radians/second), and δ denotes a phase angle (where “phase” refers to angular separation). Remember that 1 radian (~ 57˚) is that portion of a circle equal to the circle’s radius, so converting to radian notation above scales the x-propagation in “natural” rotational (or wave) terms. s θ R radius R = arc length s if θ = 1 radian (= 57.3°) What is the source of EMR? Fundamentally, EMR’s source is the acceleration of electrical charges. A convenient example of such a charge is an electron. If one electron approaches another, their paired negative charges will result in mutual repulsion. The closer they approach one another, the stronger this repulsive force (and the associated charge accelerations) will be. SO431 — EMR basics for remote sensing (8-21-09) -6- Remember that Coulomb’s law describes this force F between a pair of charges q1 and q2 by: k q1 q2 F = . R2 So the repulsive force varies inversely with the square of the charge separation R. The electric field strength vector (E) indicates the force per unit charge so that F E = q. Physically, the electric field lines are defined by the force lines. If we insert an electron into a previously vacant region of space, the charge’s presence is communicated at speed c along the electric field lines. By accelerating the electron to a new position, we have altered the field lines, producing bends or kinks in them. Because the kinks in the electric field lines propagate at the finite speed c (in a vacuum), we say that the radiation propagates at speed c. Back and forth acceleration of the electron produces oscillating field lines or waves. Note, however, that along the line of oscillation, there is no detectable displacement (and hence no electromagnetic wave). z-axis Instantaneous E pattern electron acceleration coincides with z-axis 1 kinked E-field line (x-y plane) y-axis x-axis Kinks in E-field caused by electron accelerations along z-axis radiate outward as EM waves ⊥ the x-y plane. SO431 — EMR basics for remote sensing (8-21-09) -7- The time-averaged magnitude (or amplitude) E of the electric field strength E varies as: E = qa sin(θ), R where θ is the angle between the direction of the oscillation and the direction of our detector, a is the magnitude of the electron acceleration, and R is the distance over which the acceleration occurs. In the diagram above, the z-axis corresponds to θ = 0˚, while the x-axis and y-axis (in fact, the whole x-y plane) corresponds to θ = 90˚. Now the intensity (denoted I, a measurable electromagnetic quantity) of this EM wave varies as the square of the electrical field’s magnitude. Thus I ∝ E2 sin2(θ). θ I along z-axis = 0 I( = 45°) (θ = 0°) = 0.5*E2 Time-averaged I from I in x-y plane = one accelerated 1*E2(θ = 90°) 2 electron ∝ sin (θ) We’ve just described a transmitter/emitter, in which we somehow accelerated the electrons. Conversely, if an oscillating wave “washes by” a charge that is initially at rest, the charge will accelerate in response. In this case, the electromagnetic wave does work on the charge. Now we have a receiver in which the originally stationary charge is accelerated by the presence of EMR. For convenience sake, thus far we have described EMR using wave terminology. This is appropriate because EMR often displays wavelike characteristics; e.g., interference. However, later it will be more convenient to discuss EMR using particle (or photon) terminology, as when we discuss scattering. Photons’ (massless) kinetic energies E are described by: E = h ν = h c/λ, where h = 6.626 x 10-34 J sec, Planck’s constant. How does E depend on both frequency and wavelength? SO431 — EMR basics for remote sensing (8-21-09) -8- How do we describe naturally occurring EMR? There are two main classes of descriptions that we need: 1) geometric, and 2) spectral.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Radiant Heating with Infrared
    W A T L O W RADIANT HEATING WITH INFRARED A TECHNICAL GUIDE TO UNDERSTANDING AND APPLYING INFRARED HEATERS Bleed Contents Topic Page The Advantages of Radiant Heat . 1 The Theory of Radiant Heat Transfer . 2 Problem Solving . 14 Controlling Radiant Heaters . 25 Tips On Oven Design . 29 Watlow RAYMAX® Heater Specifications . 34 The purpose of this technical guide is to assist customers in their oven design process, not to put Watlow in the position of designing (and guaranteeing) radiant ovens. The final responsibility for an oven design must remain with the equipment builder. This technical guide will provide you with an understanding of infrared radiant heating theory and application principles. It also contains examples and formulas used in determining specifications for a radiant heating application. To further understand electric heating principles, thermal system dynamics, infrared temperature sensing, temperature control and power control, the following information is also available from Watlow: • Watlow Product Catalog • Watlow Application Guide • Watlow Infrared Technical Guide to Understanding and Applying Infrared Temperature Sensors • Infrared Technical Letter #5-Emissivity Table • Radiant Technical Letter #11-Energy Uniformity of a Radiant Panel © Watlow Electric Manufacturing Company, 1997 The Advantages of Radiant Heat Electric radiant heat has many benefits over the alternative heating methods of conduction and convection: • Non-Contact Heating Radiant heaters have the ability to heat a product without physically contacting it. This can be advantageous when the product must be heated while in motion or when physical contact would contaminate or mar the product’s surface finish. • Fast Response Low thermal inertia of an infrared radiation heating system eliminates the need for long pre-heat cycles.
    [Show full text]
  • A Compilation of Data on the Radiant Emissivity of Some Materials at High Temperatures
    This is a repository copy of A compilation of data on the radiant emissivity of some materials at high temperatures. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/133266/ Version: Accepted Version Article: Jones, JM orcid.org/0000-0001-8687-9869, Mason, PE and Williams, A (2019) A compilation of data on the radiant emissivity of some materials at high temperatures. Journal of the Energy Institute, 92 (3). pp. 523-534. ISSN 1743-9671 https://doi.org/10.1016/j.joei.2018.04.006 © 2018 Energy Institute. Published by Elsevier Ltd. This is an author produced version of a paper published in Journal of the Energy Institute. Uploaded in accordance with the publisher's self-archiving policy. This manuscript version is made available under the Creative Commons CC-BY-NC-ND 4.0 license http://creativecommons.org/licenses/by-nc-nd/4.0/ Reuse This article is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs (CC BY-NC-ND) licence. This licence only allows you to download this work and share it with others as long as you credit the authors, but you can’t change the article in any way or use it commercially. More information and the full terms of the licence here: https://creativecommons.org/licenses/ Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ A COMPILATION OF DATA ON THE RADIANT EMISSIVITY OF SOME MATERIALS AT HIGH TEMPERATURES J.M Jones, P E Mason and A.
    [Show full text]
  • Spectral Reflectance and Emissivity of Man-Made Surfaces Contaminated with Environmental Effects
    Optical Engineering 47͑10͒, 106201 ͑October 2008͒ Spectral reflectance and emissivity of man-made surfaces contaminated with environmental effects John P. Kerekes, MEMBER SPIE Abstract. Spectral remote sensing has evolved considerably from the Rochester Institute of Technology early days of airborne scanners of the 1960’s and the first Landsat mul- Chester F. Carlson Center for Imaging Science tispectral satellite sensors of the 1970’s. Today, airborne and satellite 54 Lomb Memorial Drive hyperspectral sensors provide images in hundreds of contiguous narrow Rochester, New York 14623 spectral channels at spatial resolutions down to meter scale and span- E-mail: [email protected] ning the optical spectral range of 0.4 to 14 ␮m. Spectral reflectance and emissivity databases find use not only in interpreting these images but also during simulation and modeling efforts. However, nearly all existing Kristin-Elke Strackerjan databases have measurements of materials under pristine conditions. Aerospace Engineering Test Establishment The work presented extends these measurements to nonpristine condi- P.O. Box 6550 Station Forces tions, including materials contaminated with sand and rain water. In par- Cold Lake, Alberta ticular, high resolution spectral reflectance and emissivity curves are pre- T9M 2C6 Canada sented for several man-made surfaces ͑asphalt, concrete, roofing shingles, and vehicles͒ under varying amounts of sand and water. The relationship between reflectance and area coverage of the contaminant Carl Salvaggio, MEMBER SPIE is reported and found to be linear or nonlinear, depending on the mate- Rochester Institute of Technology rials and spectral region. In addition, new measurement techniques are Chester F. Carlson Center for Imaging Science presented that overcome limitations of existing instrumentation and labo- 54 Lomb Memorial Drive ratory settings.
    [Show full text]
  • Fundametals of Rendering - Radiometry / Photometry
    Fundametals of Rendering - Radiometry / Photometry “Physically Based Rendering” by Pharr & Humphreys •Chapter 5: Color and Radiometry •Chapter 6: Camera Models - we won’t cover this in class 782 Realistic Rendering • Determination of Intensity • Mechanisms – Emittance (+) – Absorption (-) – Scattering (+) (single vs. multiple) • Cameras or retinas record quantity of light 782 Pertinent Questions • Nature of light and how it is: – Measured – Characterized / recorded • (local) reflection of light • (global) spatial distribution of light 782 Electromagnetic spectrum 782 Spectral Power Distributions e.g., Fluorescent Lamps 782 Tristimulus Theory of Color Metamers: SPDs that appear the same visually Color matching functions of standard human observer International Commision on Illumination, or CIE, of 1931 “These color matching functions are the amounts of three standard monochromatic primaries needed to match the monochromatic test primary at the wavelength shown on the horizontal scale.” from Wikipedia “CIE 1931 Color Space” 782 Optics Three views •Geometrical or ray – Traditional graphics – Reflection, refraction – Optical system design •Physical or wave – Dispersion, interference – Interaction of objects of size comparable to wavelength •Quantum or photon optics – Interaction of light with atoms and molecules 782 What Is Light ? • Light - particle model (Newton) – Light travels in straight lines – Light can travel through a vacuum (waves need a medium to travel in) – Quantum amount of energy • Light – wave model (Huygens): electromagnetic radiation: sinusiodal wave formed coupled electric (E) and magnetic (H) fields 782 Nature of Light • Wave-particle duality – Light has some wave properties: frequency, phase, orientation – Light has some quantum particle properties: quantum packets (photons). • Dimensions of light – Amplitude or Intensity – Frequency – Phase – Polarization 782 Nature of Light • Coherence - Refers to frequencies of waves • Laser light waves have uniform frequency • Natural light is incoherent- waves are multiple frequencies, and random in phase.
    [Show full text]
  • Light and Illumination
    ChapterChapter 3333 -- LightLight andand IlluminationIllumination AAA PowerPointPowerPointPowerPoint PresentationPresentationPresentation bybyby PaulPaulPaul E.E.E. Tippens,Tippens,Tippens, ProfessorProfessorProfessor ofofof PhysicsPhysicsPhysics SouthernSouthernSouthern PolytechnicPolytechnicPolytechnic StateStateState UniversityUniversityUniversity © 2007 Objectives:Objectives: AfterAfter completingcompleting thisthis module,module, youyou shouldshould bebe ableable to:to: •• DefineDefine lightlight,, discussdiscuss itsits properties,properties, andand givegive thethe rangerange ofof wavelengthswavelengths forfor visiblevisible spectrum.spectrum. •• ApplyApply thethe relationshiprelationship betweenbetween frequenciesfrequencies andand wavelengthswavelengths forfor opticaloptical waves.waves. •• DefineDefine andand applyapply thethe conceptsconcepts ofof luminousluminous fluxflux,, luminousluminous intensityintensity,, andand illuminationillumination.. •• SolveSolve problemsproblems similarsimilar toto thosethose presentedpresented inin thisthis module.module. AA BeginningBeginning DefinitionDefinition AllAll objectsobjects areare emittingemitting andand absorbingabsorbing EMEM radiaradia-- tiontion.. ConsiderConsider aa pokerpoker placedplaced inin aa fire.fire. AsAs heatingheating occurs,occurs, thethe 1 emittedemitted EMEM waveswaves havehave 2 higherhigher energyenergy andand 3 eventuallyeventually becomebecome visible.visible. 4 FirstFirst redred .. .. .. thenthen white.white. LightLightLight maymaymay bebebe defineddefineddefined
    [Show full text]
  • About SI Units
    Units SI units: International system of units (French: “SI” means “Système Internationale”) The seven SI base units are: Mass: kg Defined by the prototype “standard kilogram” located in Paris. The standard kilogram is made of Pt metal. Length: m Originally defined by the prototype “standard meter” located in Paris. Then defined as 1,650,763.73 wavelengths of the orange-red radiation of Krypton86 under certain specified conditions. (Official definition: The distance traveled by light in vacuum during a time interval of 1 / 299 792 458 of a second) Time: s The second is defined as the duration of a certain number of oscillations of radiation coming from Cs atoms. (Official definition: The second is the duration of 9,192,631,770 periods of the radiation of the hyperfine- level transition of the ground state of the Cs133 atom) Current: A Defined as the current that causes a certain force between two parallel wires. (Official definition: The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 meter apart in vacuum, would produce between these conductors a force equal to 2 × 10-7 Newton per meter of length. Temperature: K One percent of the temperature difference between boiling point and freezing point of water. (Official definition: The Kelvin, unit of thermodynamic temperature, is the fraction 1 / 273.16 of the thermodynamic temperature of the triple point of water. Amount of substance: mol The amount of a substance that contains Avogadro’s number NAvo = 6.0221 × 1023 of atoms or molecules.
    [Show full text]
  • Black Body Radiation and Radiometric Parameters
    Black Body Radiation and Radiometric Parameters: All materials absorb and emit radiation to some extent. A blackbody is an idealization of how materials emit and absorb radiation. It can be used as a reference for real source properties. An ideal blackbody absorbs all incident radiation and does not reflect. This is true at all wavelengths and angles of incidence. Thermodynamic principals dictates that the BB must also radiate at all ’s and angles. The basic properties of a BB can be summarized as: 1. Perfect absorber/emitter at all ’s and angles of emission/incidence. Cavity BB 2. The total radiant energy emitted is only a function of the BB temperature. 3. Emits the maximum possible radiant energy from a body at a given temperature. 4. The BB radiation field does not depend on the shape of the cavity. The radiation field must be homogeneous and isotropic. T If the radiation going from a BB of one shape to another (both at the same T) were different it would cause a cooling or heating of one or the other cavity. This would violate the 1st Law of Thermodynamics. T T A B Radiometric Parameters: 1. Solid Angle dA d r 2 where dA is the surface area of a segment of a sphere surrounding a point. r d A r is the distance from the point on the source to the sphere. The solid angle looks like a cone with a spherical cap. z r d r r sind y r sin x An element of area of a sphere 2 dA rsin d d Therefore dd sin d The full solid angle surrounding a point source is: 2 dd sind 00 2cos 0 4 Or integrating to other angles < : 21cos The unit of solid angle is steradian.
    [Show full text]
  • Section 22-3: Energy, Momentum and Radiation Pressure
    Answer to Essential Question 22.2: (a) To find the wavelength, we can combine the equation with the fact that the speed of light in air is 3.00 " 108 m/s. Thus, a frequency of 1 " 1018 Hz corresponds to a wavelength of 3 " 10-10 m, while a frequency of 90.9 MHz corresponds to a wavelength of 3.30 m. (b) Using Equation 22.2, with c = 3.00 " 108 m/s, gives an amplitude of . 22-3 Energy, Momentum and Radiation Pressure All waves carry energy, and electromagnetic waves are no exception. We often characterize the energy carried by a wave in terms of its intensity, which is the power per unit area. At a particular point in space that the wave is moving past, the intensity varies as the electric and magnetic fields at the point oscillate. It is generally most useful to focus on the average intensity, which is given by: . (Eq. 22.3: The average intensity in an EM wave) Note that Equations 22.2 and 22.3 can be combined, so the average intensity can be calculated using only the amplitude of the electric field or only the amplitude of the magnetic field. Momentum and radiation pressure As we will discuss later in the book, there is no mass associated with light, or with any EM wave. Despite this, an electromagnetic wave carries momentum. The momentum of an EM wave is the energy carried by the wave divided by the speed of light. If an EM wave is absorbed by an object, or it reflects from an object, the wave will transfer momentum to the object.
    [Show full text]
  • Reflectometers for Absolute and Relative Reflectance
    sensors Communication Reflectometers for Absolute and Relative Reflectance Measurements in the Mid-IR Region at Vacuum Jinhwa Gene 1 , Min Yong Jeon 1,2 and Sun Do Lim 3,* 1 Institute of Quantum Systems (IQS), Chungnam National University, Daejeon 34134, Korea; [email protected] (J.G.); [email protected] (M.Y.J.) 2 Department of Physics, College of Natural Sciences, Chungnam National University, Daejeon 34134, Korea 3 Division of Physical Metrology, Korea Research Institute of Standards and Science, Daejeon 34113, Korea * Correspondence: [email protected] Abstract: We demonstrated spectral reflectometers for two types of reflectances, absolute and relative, of diffusely reflecting surfaces in directional-hemispherical geometry. Both are built based on the integrating sphere method with a Fourier-transform infrared spectrometer operating in a vacuum. The third Taylor method is dedicated to the reflectometer for absolute reflectance, by which absolute spectral diffuse reflectance scales of homemade reference plates are realized. With the reflectometer for relative reflectance, we achieved spectral diffuse reflectance scales of various samples including concrete, polystyrene, and salt plates by comparing against the reference standards. We conducted ray-tracing simulations to quantify systematic uncertainties and evaluated the overall standard uncertainty to be 2.18% (k = 1) and 2.99% (k = 1) for the absolute and relative reflectance measurements, respectively. Keywords: mid-infrared; total reflectance; metrology; primary standard; 3rd Taylor method Citation: Gene, J.; Jeon, M.Y.; Lim, S.D. Reflectometers for Absolute and 1. Introduction Relative Reflectance Measurements in Spectral diffuse reflectance in the mid-infrared (MIR) region is now of great interest the Mid-IR Region at Vacuum.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Properties of Electromagnetic Waves Any Electromagnetic Wave Must Satisfy Four Basic Conditions: 1
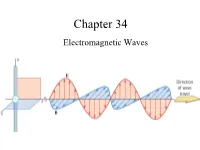
    Chapter 34 Electromagnetic Waves The Goal of the Entire Course Maxwell’s Equations: Maxwell’s Equations James Clerk Maxwell •1831 – 1879 •Scottish theoretical physicist •Developed the electromagnetic theory of light •His successful interpretation of the electromagnetic field resulted in the field equations that bear his name. •Also developed and explained – Kinetic theory of gases – Nature of Saturn’s rings – Color vision Start at 12:50 https://www.learner.org/vod/vod_window.html?pid=604 Correcting Ampere’s Law Two surfaces S1 and S2 near the plate of a capacitor are bounded by the same path P. Ampere’s Law states that But it is zero on S2 since there is no conduction current through it. This is a contradiction. Maxwell fixed it by introducing the displacement current: Fig. 34-1, p. 984 Maxwell hypothesized that a changing electric field creates an induced magnetic field. Induced Fields . An increasing solenoid current causes an increasing magnetic field, which induces a circular electric field. An increasing capacitor charge causes an increasing electric field, which induces a circular magnetic field. Slide 34-50 Displacement Current d d(EA)d(q / ε) 1 dq E 0 dt dt dt ε0 dt dq d ε E dt0 dt The displacement current is equal to the conduction current!!! Bsd μ I μ ε I o o o d Maxwell’s Equations The First Unified Field Theory In his unified theory of electromagnetism, Maxwell showed that electromagnetic waves are a natural consequence of the fundamental laws expressed in these four equations: q EABAdd 0 εo dd Edd s BE B s μ I μ ε dto o o dt QuickCheck 34.4 The electric field is increasing.
    [Show full text]