DOCSLIB.ORG

I and Q Components in Communications Signals and Single Sideband

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
I and Q Components in Communications Signals and Single Sideband I and Q Components in Communications Signals and Single Sideband 1 SHARLENE KATZ DAVID SCHWARTZ JAMES FLYNN 7/22/2010 OVERVIEW 2 Description of I and Q signal representation Advantages of using I and Q components Using I and Q to demodulate signals I and Q signal processing in the USRP Single Sideband (SSB) Processing I and Q components of a SSB signal in the USRP 7/22/2010 Standard Representation of Communications Signals 3 Modulation Time Domain Frequency Domain AM XAM(f) f -fc fc DSB FM 7/22/2010 Overview of I and Q Representation 4 I and Q are the In-phase and Quadrature components of a signal. Complete description of a signal is: x()()() t I t jQ t x(t) can therefore be represented as a vector with magnitude and phase angle. Phase angle is not absolute, but relates to some arbitrary reference. 7/22/2010 Overview of I and Q Representation 5 In Digital Signal Processing (DSP), ultimate reference is local sampling clock. DSP relies heavily on I and Q signals for processing. Use of I and Q allows for processing of signals near DC or zero frequency. If we use “real” signals (cosine) to shift a modulated signal to baseband we get sum and difference frequencies If we use a “complex” sinusoid to shift a modulated signal to baseband we ONLY get the sum This avoids problems with images 7/22/2010 Overview of I and Q Representation 6 Nyquist frequency is twice highest frequency, not twice bandwidth of signal. For example: common frequency used in analog signal processing is 455 kHz. To sample in digital processing, requires 910 kS/s. But if the signal bandwidth is only 10 kHz. With I & Q, sampling requires only 20 kS/s. 7/22/2010 Overview of I and Q Representation 7 I and Q allows discerning of positive and negative frequencies. If : H() f a jb Then: H() f a jb 7/22/2010 Overview of I and Q Representation 8 Representing familiar characteristics of a signal with I and Q: 22 • Amplitude: A()()() t I t Q t • Phase: 1 Qt() (t ) tan It() • Frequency: Q()() t I t I()() t Q t ()t ft()tt t I22()() t Q t 7/22/2010 DEMODULATION 9 AM: x()()() t i22 t q t SSB: x()() t i t 11 i ()(1) t q t q ()(1) t i t FM: xt( ) tan t i( t ) i ( t 1) q ( t ) q ( t 1) 1 qt() PM: xt( ) tan it() 7/22/2010 Overview of I and Q Representation 10 The traditional FM equation: x( t ) cos( t k x ( t ) dt ) FM c m The analytic equation: xFM( t ) I ( t )cos( c t ) jQ ( t )sin( c t ) Modulation and Demodulation methods are different when I and Q representation is used 7/22/2010 USRP DAUGHTER BOARD 11 LPF ADC I AMP cos ωc t LPF ADC Q sin ωc t 7/22/2010 FPGA 12 cos ωf tn n = sample number I decimate I complex To USB multiply and PC Q decimate Q sin ωf tn 7/22/2010 Complex Multiply 13 cos (ω t ) I f n I Q Q cos (ωf tn ) (A + j B) * (C + j D) = AC – BD + j (BC + AD) cos t + I + j Q f sinft 7/22/2010 Sideband Modulation 14 Where’s the intelligence? A signal carries useful information only when it changes. Change of ANY carrier parameter produces sidebands. The intelligence or information is in the sidebands. Why not just send the sidebands or just a sideband? 7/22/2010 AM Review 15 AM review: Carrier is modulated by varying amplitude linearly proportional to intelligence (baseband) signal amplitude. Block Diagram m x x(t) + xAM(t)=Ac [1+mx(t)]cos ct Accosct 7/22/2010 AM: Time Domain 16 AM in the Time Domain 100% modulated Unmodulated carrier carrier 7/22/2010 AM: Frequency Domain 17 AM in the Frequency Domain carrier lower upper sideband sideband 7/22/2010 Double Sideband Modulation (DSB) 18 Let’s just transmit the sidebands x(t) m x + xDSB(t) = Ac*m*x(t)*cosct Accosct X 7/22/2010 DSB: Time Domain 19 Double Sideband in the Time Domain 7/22/2010 DSB: Frequency Domain 20 Double Sideband in the Frequency Domain carrier was here lower upper sideban sideband d 7/22/2010 Example of a DSB Signal 21 7/22/2010 DSB Spectrum 22 Note: the upper and lower sidebands are the same Do we need both of them? carrier was here lower upper sideband sideband 7/22/2010 SSB Signals 23 A sideband signal is obtained by adding a sideband filter to capture the upper or lower sideband. Low Pass Filter f f f Lower x(t) x Sideband Filter Accosct f 7/22/2010 Example of a USB Signal 24 7/22/2010 Comparison of DSB and SSB 25 Power: SSB requires half of the power of DSB Bandwidth: SSB requires half of the bandwidth of DSB Complexity: SSB modulators/demodulators are more complex 7/22/2010 SSB Example 26 Start with arbitrary waveform in baseband: 7/22/2010 SSB Example 27 Modulate as Upper Sideband Signal: 7/22/2010 SSB Example LPF ADC I AMP cos ωc t LPF ADC Q sin ωc t 28 7/22/2010 SSB Example 29 LPF ADC I AMP cos ωc t LPF AD Q C sin ωc t 7/22/2010 SSB Example LPF ADC I AMP cos ωc t LPF ADC Q sin ωc t 30 7/22/2010 SSB Example LPF ADC I AMP cos ωc t LPF AD Q C sin ωc t 31 7/22/2010 SSB Example LPF ADC I AMP cos ωc t LPF ADC Q sin ωc t 32 7/22/2010 SSB Example cos ωf tn n = sample number I decimate I complex To USB multiply and PC Q decimate Q sin ωf tn 33 7/22/2010 SSB Example cos ωf tn n = sample number I decimate I complex To USB multiply and PC Q decimate Q sin ωf tn 34 7/22/2010 SSB Example cos ωf tn n = sample number I decimate I complex To USB multiply and PC Q decimate Q sin ωf tn 35 7/22/2010 SSB Example cos ωf tn n = sample number I decimate I complex To USB multiply and PC Q decimate Q sin ωf tn 36 7/22/2010 Practical SSB Reception 37 Example above assumed no other signals on the band and perfectly synchronized oscillators Need to isolate (filter) the signal of interest and deal with oscillators slightly out of sync GRC tutorial demonstrates Weaver’s Method of demodulating SSB that solves these problems 7/22/2010.
Load more

Recommended publications
  • Optical Single Sideband for Broadband and Subcarrier Systems
    University of Alberta Optical Single Sideband for Broadband And Subcarrier Systems Robert James Davies 0 A thesis submitted to the faculty of Graduate Studies and Research in partial fulfillrnent of the requirernents for the degree of Doctor of Philosophy Department of Electrical And Computer Engineering Edmonton, AIberta Spring 1999 National Library Bibliothèque nationale du Canada Acquisitions and Acquisitions et Bibliographie Services services bibliographiques 395 Wellington Street 395, rue Wellington Ottawa ON KlA ON4 Ottawa ON KIA ON4 Canada Canada Yom iUe Votre relérence Our iSie Norre reference The author has granted a non- L'auteur a accordé une licence non exclusive licence allowing the exclusive permettant à la National Library of Canada to Bibliothèque nationale du Canada de reproduce, loan, distribute or sell reproduire, prêter, distribuer ou copies of this thesis in microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/nlm, de reproduction sur papier ou sur format électronique. The author retains ownership of the L'auteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fkom it Ni la thèse ni des extraits substantiels may be printed or otheMrise de celle-ci ne doivent être Unprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation. Abstract Radio systems are being deployed for broadband residential telecommunication services such as broadcast, wideband lntemet and video on demand. Justification for radio delivery centers on mitigation of problems inherent in subscriber loop upgrades such as Fiber to the Home (WH)and Hybrid Fiber Coax (HFC).
    [Show full text]
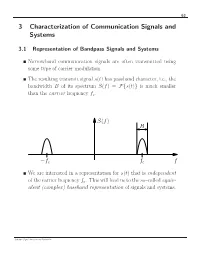
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • Radio Communications in the Digital Age
    Radio Communications In the Digital Age Volume 1 HF TECHNOLOGY Edition 2 First Edition: September 1996 Second Edition: October 2005 © Harris Corporation 2005 All rights reserved Library of Congress Catalog Card Number: 96-94476 Harris Corporation, RF Communications Division Radio Communications in the Digital Age Volume One: HF Technology, Edition 2 Printed in USA © 10/05 R.O. 10K B1006A All Harris RF Communications products and systems included herein are registered trademarks of the Harris Corporation. TABLE OF CONTENTS INTRODUCTION...............................................................................1 CHAPTER 1 PRINCIPLES OF RADIO COMMUNICATIONS .....................................6 CHAPTER 2 THE IONOSPHERE AND HF RADIO PROPAGATION..........................16 CHAPTER 3 ELEMENTS IN AN HF RADIO ..........................................................24 CHAPTER 4 NOISE AND INTERFERENCE............................................................36 CHAPTER 5 HF MODEMS .................................................................................40 CHAPTER 6 AUTOMATIC LINK ESTABLISHMENT (ALE) TECHNOLOGY...............48 CHAPTER 7 DIGITAL VOICE ..............................................................................55 CHAPTER 8 DATA SYSTEMS .............................................................................59 CHAPTER 9 SECURING COMMUNICATIONS.....................................................71 CHAPTER 10 FUTURE DIRECTIONS .....................................................................77 APPENDIX A STANDARDS
    [Show full text]
  • Lecture 25 Demodulation and the Superheterodyne Receiver EE445-10
    EE447 Lecture 6 Lecture 25 Demodulation and the Superheterodyne Receiver EE445-10 HW7;5-4,5-7,5-13a-d,5-23,5-31 Due next Monday, 29th 1 Figure 4–29 Superheterodyne receiver. m(t) 2 Couch, Digital and Analog Communication Systems, Seventh Edition ©2007 Pearson Education, Inc. All rights reserved. 0-13-142492-0 1 EE447 Lecture 6 Synchronous Demodulation s(t) LPF m(t) 2Cos(2πfct) •Only method for DSB-SC, USB-SC, LSB-SC •AM with carrier •Envelope Detection – Input SNR >~10 dB required •Synchronous Detection – (no threshold effect) •Note the 2 on the LO normalizes the output amplitude 3 Figure 4–24 PLL used for coherent detection of AM. 4 Couch, Digital and Analog Communication Systems, Seventh Edition ©2007 Pearson Education, Inc. All rights reserved. 0-13-142492-0 2 EE447 Lecture 6 Envelope Detector C • Ac • (1+ a • m(t)) Where C is a constant C • Ac • a • m(t)) 5 Envelope Detector Distortion Hi Frequency m(t) Slope overload IF Frequency Present in Output signal 6 3 EE447 Lecture 6 Superheterodyne Receiver EE445-09 7 8 4 EE447 Lecture 6 9 Super-Heterodyne AM Receiver 10 5 EE447 Lecture 6 Super-Heterodyne AM Receiver 11 RF Filter • Provides Image Rejection fimage=fLO+fif • Reduces amplitude of interfering signals far from the carrier frequency • Reduces the amount of LO signal that radiates from the Antenna stop 2/22 12 6 EE447 Lecture 6 Figure 4–30 Spectra of signals and transfer function of an RF amplifier in a superheterodyne receiver. 13 Couch, Digital and Analog Communication Systems, Seventh Edition ©2007 Pearson Education, Inc.
    [Show full text]
  • 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders
    /7 7.3.5 Fiber-Optic Cables (FO) 7.3.6 Telephone Company Unes (TELCO) 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders 7.4 Transmission Security 8. Consumer Equipment Issues 8.1 Complexity of Receivers 8.2 Receiver Input/Output Characteristics 8.2.1 RF Interface 8.2.2 Baseband Video Interface 8.2.3 Baseband Audio Interface 8.2.4 Interfacing with Ancillary Signals 8.2.5 Receiver Antenna Systems Requirements 8.3 Compatibility with Existing NTSC Consumer Equipment 8.3.1 RF Compatibility 8.3.2 Baseband Video Compatibility 8.3.3 Baseband Audio Compatibility 8.3.4 IDTV Receiver Compatibility 8.4 Allows Multi-Standard Display Devices 9. Other Considerations 9.1 Practicality of Near-Term Technological Implementation 9.2 Long-Term Viability/Rate of Obsolescence 9.3 Upgradability/Extendability 9.4 Studio/Plant Compatibility Section B: EXPLANATORY NOTES OF ATTRIBUTES/SYSTEMS MATRIX Items on the Attributes/System Matrix for which no explanatory note is provided were deemed to be self-explanatory. I. General Description (Proponent) section I shall be used by a system proponent to define the features of the system being proposed. The features shall be defined and organized under the headings ot the following subsections 1 through 4. section I. General Description (Proponent) shall consist of a description of the proponent system in narrative form, which covers all of the features and characteris­ tics of the system which the proponent wishe. to be included in the public record, and which will be used by various groups to analyze and understand the system proposed, and to compare with other propo.ed systems.
    [Show full text]
  • Of Single Sideband Demodulation by Richard Lyons
    Understanding the 'Phasing Method' of Single Sideband Demodulation by Richard Lyons There are four ways to demodulate a transmitted single sideband (SSB) signal. Those four methods are: • synchronous detection, • phasing method, • Weaver method, and • filtering method. Here we review synchronous detection in preparation for explaining, in detail, how the phasing method works. This blog contains lots of preliminary information, so if you're already familiar with SSB signals you might want to scroll down to the 'SSB DEMODULATION BY SYNCHRONOUS DETECTION' section. BACKGROUND I was recently involved in trying to understand the operation of a discrete SSB demodulation system that was being proposed to replace an older analog SSB demodulation system. Having never built an SSB system, I wanted to understand how the "phasing method" of SSB demodulation works. However, in searching the Internet for tutorial SSB demodulation information I was shocked at how little information was available. The web's wikipedia 'single-sideband modulation' gives the mathematical details of SSB generation [1]. But SSB demodulation information at that web site was terribly sparse. In my Internet searching, I found the SSB information available on the net to be either badly confusing in its notation or downright ambiguous. That web- based material showed SSB demodulation block diagrams, but they didn't show spectra at various stages in the diagrams to help me understand the details of the processing. A typical example of what was frustrating me about the web-based SSB information is given in the analog SSB generation network shown in Figure 1. x(t) cos(ωct) + 90o 90o y(t) – sin(ωct) Meant to Is this sin(ω t) represent the c Hilbert or –sin(ωct) Transformer.
    [Show full text]
  • Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System
    Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System Kang Hsia Abstract: Telecommunications industry has widely adopted single sideband (SSB or complex quadrature) transmitter and receiver system, and one popular implementation for SSB system is to achieve image rejection through quadrature component image cancellation. Typically, during the SSB system characterization, the baseband fundamental tone and also the harmonic distortion products are important parameters besides image and LO feedthrough leakage. To ensure accurate characterization, the actual frequency locations of the harmonic distortion products are critical. While system designers may be tempted to assume that the harmonic distortion products are simply up-converted in the same fashion as the baseband fundamental frequency component, the actual distortion products may have surprising results and show up on the different side of spectrum. This paper discusses the theory of SSB system and the actual location of the baseband harmonic distortion products. Introduction Communications engineers have utilized SSB transmitter and receiver system because it offers better bandwidth utilization than double sideband (DSB) transmitter system. The primary cause of bandwidth overhead for the double sideband system is due to the image component during the mixing process. Given data transmission bandwidth of B, the former requires minimum bandwidth of B whereas the latter requires minimum bandwidth of 2B. While the filtering of the image component is one type of SSB implementation, another type of SSB system is to create a quadrature component of the signal and ideally cancels out the image through phase cancellation. M(t) M(t) COS(2πFct) Baseband Message Signal (BB) Modulated Signal (RF) COS(2πFct) Local Oscillator (LO) Signal Figure 1.
    [Show full text]
  • Baseband Video Testing with Digital Phosphor Oscilloscopes
    Application Note Baseband Video Testing With Digital Phosphor Oscilloscopes Video signals are complex pose instrument that can pro- This application note demon- waveforms comprised of sig- vide accurate information – strates the use of a Tektronix nals representing a picture as quickly and easily. Finally, to TDS 700D-series Digital well as the timing informa- display all of the video wave- Phosphor Oscilloscope to tion needed to display the form details, a fast acquisi- make a variety of common picture. To capture and mea- tion technology teamed with baseband video measure- sure these complex signals, an intensity-graded display ments and examines some of you need powerful instru- give the confidence and the critical measurement ments tailored for this appli- insight needed to detect and issues. cation. But, because of the diagnose problems with the variety of video standards, signal. you also need a general-pur- Copyright © 1998 Tektronix, Inc. All rights reserved. Video Basics Video signals come from a for SMPTE systems, etc. The active portion of the video number of sources, including three derived component sig- signal. Finally, the synchro- cameras, scanners, and nals can then be distributed nization information is graphics terminals. Typically, for processing. added. Although complex, the baseband video signal Processing this composite signal is a sin- begins as three component gle signal that can be carried analog or digital signals rep- In the processing stage, video on a single coaxial cable. resenting the three primary component signals may be combined to form a single Component Video Signals. color elements – the Red, Component signals have an Green, and Blue (RGB) com- composite video signal (as in NTSC or PAL systems), advantage of simplicity in ponent signals.
    [Show full text]
  • Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
    Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse.
    [Show full text]
  • An Analysis of a Quadrature Double-Sideband/Frequency Modulated Communication System
    Scholars' Mine Masters Theses Student Theses and Dissertations 1970 An analysis of a quadrature double-sideband/frequency modulated communication system Denny Ray Townson Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Electrical and Computer Engineering Commons Department: Recommended Citation Townson, Denny Ray, "An analysis of a quadrature double-sideband/frequency modulated communication system" (1970). Masters Theses. 7225. https://scholarsmine.mst.edu/masters_theses/7225 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. AN ANALYSIS OF A QUADRATURE DOUBLE- SIDEBAND/FREQUENCY MODULATED COMMUNICATION SYSTEM BY DENNY RAY TOWNSON, 1947- A THESIS Presented to the Faculty of the Graduate School of the UNIVERSITY OF MISSOURI - ROLLA In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN ELECTRICAL ENGINEERING 1970 ii ABSTRACT A QDSB/FM communication system is analyzed with emphasis placed on the QDSB demodulation process and the AGC action in the FM transmitter. The effect of noise in both the pilot and message signals is investigated. The detection gain and mean square error is calculated for the QDSB baseband demodulation process. The mean square error is also evaluated for the QDSB/FM system. The AGC circuit is simulated on a digital computer. Errors introduced into the AGC system are analyzed with emphasis placed on nonlinear gain functions for the voltage con­ trolled amplifier.
    [Show full text]
  • NRSC-G202 FM IBOC Total Digital Sideband Power
    NRSC GUIDELINE NATIONAL RADIO SYSTEMS COMMITTEE NRSC-G202-A FM IBOC Total Digital Sideband Power for Various Configurations April 2016 NAB: 1771 N Street, N.W. 1919 South Eads Street Washington, DC 20036 Arlington, VA 22202 Tel: 202-429-5356 Tel: 703-907-7660 Co-sponsored by the Consumer Technology Association and the National Association of Broadcasters http://www.nrscstandards.org NRSC GUIDELINE NATIONAL RADIO SYSTEMS COMMITTEE NRSC-G202-A FM IBOC Total Digital Sideband Power for Various Configurations April 2016 NAB: 1771 N Street, N.W. 1919 South Eads Street Washington, DC 20036 Arlington, VA 22202 Tel: 202-429-5356 Fax: 202-517-1617 Tel: 703-907-4366 Fax: 703-907-4158 Co-sponsored by the Consumer Technology Association and the National Association of Broadcasters http://www.nrscstandards.org NRSC-G202-A NOTICE NRSC Standards, Guidelines, Reports and other technical publications are designed to serve the public interest through eliminating misunderstandings between manufacturers and purchasers, facilitating interchangeability and improvement of products, and assisting the purchaser in selecting and obtaining with minimum delay the proper product for his particular need. Existence of such Standards, Guidelines, Reports and other technical publications shall not in any respect preclude any member or nonmember of the Consumer Technology Association (CTA) or the National Association of Broadcasters (NAB) from manufacturing or selling products not conforming to such Standards, Guidelines, Reports and other technical publications, nor shall the existence of such Standards, Guidelines, Reports and other technical publications preclude their voluntary use by those other than CTA or NAB members, whether to be used either domestically or internationally.
    [Show full text]
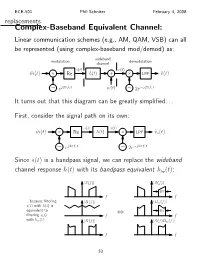
  • The Complex-Baseband Equivalent Channel Model
    ECE-501 Phil Schniter February 4, 2008 replacements Complex-Baseband Equivalent Channel: Linear communication schemes (e.g., AM, QAM, VSB) can all be represented (using complex-baseband mod/demod) as: wideband modulation demodulation channel s(t) r(t) m˜ (t) Re h(t) + LPF v˜(t) × × j2πfct w(t) j2πfct ∼ e ∼ 2e− It turns out that this diagram can be greatly simplified. First, consider the signal path on its own: s(t) x(t) m˜ (t) Re h(t) LPF v˜s(t) × × j2πfct j2πfct ∼ e ∼ 2e− Since s(t) is a bandpass signal, we can replace the wideband channel response h(t) with its bandpass equivalent hbp(t): S(f) S(f) | | | | 2W f f ...because filtering H(f) Hbp(f) s(t) with h(t) is | | | | equivalent to 2W filtering s(t) f ⇔ f with hbp(t): X(f) S(f)H (f) | | | bp | f f 33 ECE-501 Phil Schniter February 4, 2008 Then, notice that j2πfct j2πfct s(t) h (t) 2e− = s(τ)h (t τ)dτ 2e− ∗ bp bp − · # ! " j2πfcτ j2πfc(t τ) = s(τ)2e− h (t τ)e− − dτ bp − # j2πfct j2πfct = s(t)2e− h (t)e− , ∗ bp which means we can rewrit!e the block di"agr!am as " s(t) j2πfct m˜ (t) Re hbp(t)e− LPF v˜s(t) × × j2πfct j2πfct ∼ e ∼ 2e− j2πfct We can now reverse the order of the LPF and hbp(t)e− (since both are LTI systems), giving s(t) j2πfct m˜ (t) Re LPF hbp(t)e− v˜s(t) × × j2πfct j2πfct ∼ e ∼ 2e− Since mod/demod is transparent (with synched oscillators), it can be removed, simplifying the block diagram to j2πfct m˜ (t) hbp(t)e− v˜s(t) 34 ECE-501 Phil Schniter February 4, 2008 Now, since m˜ (t) is bandlimited to W Hz, there is no need to j2πfct model the left component of Hbp(f + f ) = hbp(t)e− : c F{ } Hbp(f) Hbp(f + fc) H˜ (f) | | | | | | f f f fc fc 2fc 0 B 0 B − − − j2πfct Replacing hbp(t)e− with the complex-baseband response h˜(t) gives the “complex-baseband equivalent” signal path: m˜ (t) h˜(t) v˜s(t) The spectrums above show that h (t) = Re h˜(t) 2ej2πfct .
    [Show full text]