DOCSLIB.ORG

Mass Chains of Light Hypernuclei and Separation Energies of Mirror Hypernuclei from BWMH Mass Formula

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mass Chains of Light Hypernuclei and Separation Energies of Mirror Hypernuclei from BWMH Mass Formula Mass Chains of Light Hypernuclei and Separation Energies of Mirror Hypernuclei from BWMH Mass Formula A. Armat1 and H. Hassanabadi1* 1Physics Department, University of Shahrood, Shahrood, Iran *[email protected] Abstract In this work, by using generalized semi-empirical mass formula, decay chains of light hypernuclei for odd-A and even-A are calculated and the unstable hypernuclei of mass chains are indicated. The separation energy per baryon of the mirror hypernuclei is obtained. Keywords: Hypernuclei, Mass formula, Binding energy, Mass chains, Separation energy PACS numbers: 21.80.+a, 25.80.-e, 21.10.Dr, 32.10.Bi, 12.90.+b 1. Introduction Hypernuclear physics is an important branch of nuclear physics and has attracted lots of attention during the past decades. Many novel phenomena have been discovered in this field and many others are anticipated. Hypernuclei are bound systems of nucleons with one or more strange baryons (hyperons), which contain the strange quark. These systems provide us with a reliable basis to investigate many nuclear and particle systems [1].) The hypernuclei physics has been progressing quite rapidly in both experimental and theoretical backgrounds [2, 3].). Hypernuclei are typically produced in some excited states through hadronic reactions such (K , ) or (,K). Nevertheless, they can reach their ground state through electromagnetic and/or nucleon emission [4]. The study of hypernuclei provides us with a deeper insight into fundamental interactions where particle reactions are not accessible such as the hyperon- nucleon [5-6] and hyperon-hyperon interactions. Information on these interactions is only possible through the study of the production and decay of hypernuclei which makes the field quite vital for related studies [7]. The research on the structure and property of hypernuclei had produced many meaningful results in 1970s. The hypernuclei properties include well depth of -nuclear potential, the shrinkage of hypernuclear size [8-9], hypernuclear spins and life times, hypernuclei spectroscopy[10], excited states of hypernuclei, and binding energy per baryon and the hyperon binding energy [11]. The total nuclear binding energy of any nucleus plays a crucial role in nuclear stability and can be therefore used to examine the single nucleon binding near the drip-line regime. The binding energies in single hypernuclei with in different single-particle states is obtained by Xue et al. with the spherical and the triaxial RMF calculations [12] .The semi empirical mass formula proposed by Bethe-Weizsäcker was generalized for light nuclei (BWM)[13-16] and the more improved version (BWMH) which works well for both strange and nonstrange nuclei was developed recently [17]. We use BWMH to compute decay chains of light Hypernuclei for odd-A and even-A. The unstable hypernuclei of mass chains is shown in Fig. 1 and Fig. 2. Proton, neutron and Lambda hyperon of mirror strange nuclei separation energies and binding energy are reported in Table 1. The separation energies difference is shown in Fig. 3. The binding energy difference and baryons separation energies difference between the number of mirror hypernuclei and mirror nuclei are compared in Figs. 4, 5 and 6. 2. Generalized Semi-Empirical Mass Formula Semiempirical mass formula for hypernuclei is M(A,Z) M(A,zcY ) M B(A,Z) (1) where M(A,Z) and MY denote the hypernuclei mass and hyperon mass, respectively. M(A,zc ) is the nucleus mass M(A,z ) M B(A,z ) (2) ccN B(A,zc ) and B(A,Z) are respectively the binding energies of a nucleus and hypernucleus. A is the total number of baryon and Z is defined as Z zc n Y q Y (3) Y where nY is the number of hyperons of a particular kind in a nucleus, zc denotes the number of protons, qY is the charge number (with proper sign) of hyperon(s) constituting the hypernucleus and MN , the nucleon mass, is MN z c m p nm n (4) where m is the proton mass, m denotes the neutron mass, and n is the number p n of neutrons. We consider the generalized mass formula for non-strange, strange and multiply-strange nuclear systems [17] 2 2 Z(Z 1) a (n z ) 3 sym c A B(A, Z) a A asc 4A a1 (1 exp( )) 3 (1 exp(A ))A 30 A 17 2 3 nYY [0.0335(m ) 26.7 48.7 S A Y 2 2 A/17 aYc {(N z ) (N n) }/{(1 e )A}] (5) where mY is the mass of hyperon in MeV, S is the strange number of hyperon and N shows the total number of hyperons. Parameter a Y is introduced to consider the hyperon number asymmetry with respect to the proton and neutron numbers. The pairing energy is 1/2 12A for even n even zc 1/2 12A for odd n odd zc (6) 0 for odd A We calculated mass chains for A=25 and A=24. Fig. 1 shows a decay chain for A= 24. The unstable hypernuclei approach stability by converting a neutron into a proton or a proton into a neutron. Fig. 2 shows the mass chains of hypernuclei for A=25. For this A, the pairing term gives two parabolas. For constant A, Eq. (5) represents a parabola of M vs Z. The parabola will be centered about the point where (5) reaches a minimum. We must find the minimum, where M zc 0 1.42 185.68 mm A1 3 1 e A 17 np z (7) cmin 2.84 371.36 A1 3 A(1 e A 17 ) which gives 46.42(A 2z )2 M 36.68A2 3 31.554A cmin m (A z ) m z M 2(1 e A 30 ) minA(1 eA 17 ) n cmin p c min 1.42(1 z n q )( z n q ) 48.7 S ccmin min n ( 26.7 0.0335M ) (8) AA1 3 2 3 Other useful and interesting properties which are often considered are the neutron, proton and hyperon separation energies. The hyperon separation energy SY is the amount of energy required to remove a hyperon from a hypernuclei, or equivalently the difference in binding energies between initial and final hypernuclei states. The generalized hyperon separation energy SY is defined as SY B(A,Z) hyper B(A n Y ,Z) hyper (9) Y where B(A,Z) is the binding energy of a hypernucleus and the separation energies for neutron and proton are Sn B(A, Z) hyper B(A 1,Z) hyper Sp B(A, Z) hyper B(A 1,Z 1) hyper (10) Their respective binding energies provide necessary guidelines for studying the nuclear stability near the drip lines against decay by emission of protons or neutrons. 3. Conclusions The study of hypernuclei is one of the important developing areas of nuclear physics. At present most of the information on hypernuclei has been extracted from (k , )reactions. Major goals of hypernuclear physics are to understand baryon-baryon interactions and the structure of multi-strangeness systems. In this work, We used the values of a 15.777MeV , as 18.34MeV ,ac 0.71MeV , asym 23.21MeV , k 17MeV , c 30MeV and aY 0.02 . By using the generalized semi-empirical mass formula, decay chains of light hypernuclei for odd-A and even-A are calculated. The unstable hypernuclei of decay chains is shown in Fig. 1 and Fig. 2. Proton, neutron and Lambda hyperon of mirror strange nuclei separation energies and binding energy are reported in Table 1. The separation energies difference is shown in Fig. 3. The binding energy difference and baryons separation energies difference between the number of mirror hypernuclei and mirror nuclei are compared in Figs. 4, 5 and 6. References [1] A. Parre˜no Lect. Notes Phys. 724, 141–189 (2007). [2] A. Gal and D. J. Millener, Hyperfine Interact. 210, 77 (2012). [3] C. Rappold et al, Phys. Rev. C 88, 041001 (2013). [4] A. Parreno and A. Ramos, Phys. Rev. C, 56, 1 (1997). [5] Bo-Chao Liu, Nuclear Physics A 00 1–4 (2013). [6] A. Ohnishi et al., Nuclear Physics A 00 1–8 (2013). [7] A. Parre˜no Lect. Notes Phys. 724, 141–189 (2007). [8] Motoba et al., PTP70 189(1983). [9]E. Hiyama, et al.,Phys. Rev. C 59 2351(1999). [10] Hashimoto O and Tamura H, Prog.Part.Nucl.Phys. 57 564 (2006). [11] Lan Mi-Xiang et al , Chinese Phys. Lett. 26 072101 (2009). [12] W. X. Xue, J. M. Yao, K. Hagino, Z. P. Li, H. Mei, and Y. Tanimura, Phys. Rev. C 91, 024327 –(2015). [13] C. Samanta and S. Adhikari , Phys. Rev. C 65, 037301 (2002). [14] César Barbero, Jorge G. Hirsch , Alejandro E. Mariano, Nuclear Physics A 874 (2012). [15] C. C. Barros, Jr. and Y. Hama, Phys. Rev. C, 63, 065203 (2001). [16] Z. Hasan, V. Kumar, and Daksh Lohiya, Proceedings of the DAE Symp. on Nucl. Phys. 57 (2012). [17] C. Samanta, P. Roy Chowdhury and D.N. Basu, J. Phys. G: Nucl. Part. Phys. 32, 363. (2006). TABLE 1: Binding energy and separation energies of mirror hypernuclei B Sn Sp S 4 5.0017 28.7415 2.8134 0.0282 4 4.1072 25.4819 8.3215 0.1183 H He 6 26.9775 7.7054 19.1623 5.2093 6 25.4146 20.0906 19.1623 5.3072 He Li 8 47.4405 9.9172 14.5226 8.3345 8 45.3105 16.1042 7.7827 8.4315 Li Be 10 67.3795 8.3786 14.8961 10.4581 10 64.7431 17.0384 5.7421 10.5523 Be B 12 87.0819 10.9126 11.6769 12.0160 12 83.9807 14.3222 7.8113 12.1072 B C 14 106.646 8.9646 13.1591 13.2202 14 103.111 16.2671 5.4296 13.3086 C N 16 126.108 11.6430 10.1279 14.1867 16 122.164 13.6683 7.6983 14.2724 N O 18 145.478 9.4182 12.0629 14.9846 18 141.143 16.012 5.0835 15.0680 O F 20 164.7560 12.1936 9.0351 15.6582 20 160.047 13.3736 7.4854 15.7394 F Ne 22 183.9390 9.7827 11.2146 16.2370 22 178.871 15.9261 4.7175 16.3162 Ne Na 24 201.724 12.6225 8.1604 16.7415 24 185.479 13.2310 4.5310 16.8189 Na Mg 26 222.00 10.0956 10.4879 17.1867 26 216.2480 15.9049 4.3436 17.2624 Mg Al 28 240.8690 12.9761 7.4103 17.5836 28 234.79 13.1645 6.8969 17.6577 Al Si 30 259.623 10.3665 9.8289 17.9405 30 253.225 15.9101 3.9684 18.0132 Si P 20 151.3150 5.4990 18.1333 16.3919 20 127.7740 21.7322 0.0513 16.6294 N Mg 18 141.6120 8.1967 14.3425 15.2376 18 128.608 17.9062 3.4766 15.4878 N Ne 17 133.415 7.3066 12.2734 13.4426 17 125.131 15.8236
Load more

Recommended publications
  • Arxiv:1904.10318V1 [Nucl-Th] 20 Apr 2019 Ucinltheory
    Nuclear structure investigation of even-even Sn isotopes within the covariant density functional theory Y. EL BASSEM1, M. OULNE2 High Energy Physics and Astrophysics Laboratory, Department of Physics, Faculty of Sciences SEMLALIA, Cadi Ayyad University, P.O.B. 2390, Marrakesh, Morocco. Abstract The current investigation aims to study the ground-state properties of one of the most interesting isotopic chains in the periodic table, 94−168Sn, from the proton drip line to the neutron drip line by using the covariant density functional theory, which is a modern theoretical tool for the description of nuclear structure phenomena. The physical observables of interest include the binding energy, separation energy, two-neutron shell gap, rms-radii for protons and neutrons, pairing energy and quadrupole deformation. The calculations are performed for a wide range of neutron numbers, starting from the proton-rich side up to the neutron-rich one, by using the density- dependent meson-exchange and the density dependent point-coupling effec- tive interactions. The obtained results are discussed and compared with available experimental data and with the already existing results of rela- tivistic Mean Field (RMF) model with NL3 functional. The shape phase transition for Sn isotopic chain is also investigated. A reasonable agreement is found between our calculated results and the available experimental data. Keywords: Ground-state properties, Sn isotopes, covariant density functional theory. arXiv:1904.10318v1 [nucl-th] 20 Apr 2019 1. INTRODUCTION In nuclear
    [Show full text]
  • Range of Usefulness of Bethe's Semiempirical Nuclear Mass Formula
    RANGE OF ..USEFULNESS OF BETHE' S SEMIEMPIRIC~L NUCLEAR MASS FORMULA by SEKYU OBH A THESIS submitted to OREGON STATE COLLEGE in partial fulfillment or the requirements tor the degree of MASTER OF SCIENCE June 1956 TTPBOTTDI Redacted for Privacy lrrt rtllrt ?rsfirror of finrrtor Ia Ohrr;r ef lrJer Redacted for Privacy Redacted for Privacy 0hrtrurn of tohoot Om0qat OEt ttm Redacted for Privacy Dru of 0rrdnrtr Sohdbl Drta thrrlr tr prrrEtrl %.ifh , 1,,r, ," r*(,-. ttpo{ by Brtty Drvlr ACKNOWLEDGMENT The author wishes to express his sincere appreciation to Dr. G. L. Trigg for his assistance and encouragement, without which this study would not have been concluded. The author also wishes to thank Dr. E. A. Yunker for making facilities available for these calculations• • TABLE OF CONTENTS Page INTRODUCTION 1 NUCLEAR BINDING ENERGIES AND 5 SEMIEMPIRICAL MASS FORMULA RESEARCH PROCEDURE 11 RESULTS 17 CONCLUSION 21 DATA 29 f BIBLIOGRAPHY 37 RANGE OF USEFULNESS OF BETHE'S SEMIEMPIRICAL NUCLEAR MASS FORMULA INTRODUCTION The complicated experimental results on atomic nuclei haYe been defying definite interpretation of the structure of atomic nuclei for a long tfme. Even though Yarious theoretical methods have been suggested, based upon the particular aspects of experimental results, it has been impossible to find a successful theory which suffices to explain the whole observed properties of atomic nuclei. In 1936, Bohr (J, P• 344) proposed the liquid drop model of atomic nuclei to explain the resonance capture process or nuclear reactions. The experimental evidences which support the liquid drop model are as follows: 1. Substantially constant density of nuclei with radius R - R Al/3 - 0 (1) where A is the mass number of the nucleus and R is the constant of proportionality 0 with the value of (1.5! 0.1) x 10-lJcm~ 2.
    [Show full text]
  • Modern Physics to Which He Did This Observation, Usually to Within About 0.1%
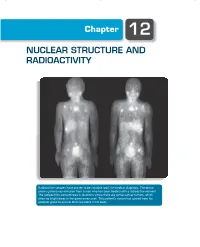
    Chapter 12 NUCLEAR STRUCTURE AND RADIOACTIVITY Radioactive isotopes have proven to be valuable tools for medical diagnosis. The photo shows gamma-ray emission from a man who has been treated with a radioactive element. The radioactivity concentrates in locations where there are active cancer tumors, which show as bright areas in the gamma-ray scan. This patient’s cancer has spread from his prostate gland to several other locations in his body. 370 Chapter 12 | Nuclear Structure and Radioactivity The nucleus lies at the center of the atom, occupying only 10−15 of its volume but providing the electrical force that holds the atom together. Within the nucleus there are Z positive charges. To keep these charges from flying apart, the nuclear force must supply an attraction that overcomes their electrical repulsion. This nuclear force is the strongest of the known forces; it provides nuclear binding energies that are millions of times stronger than atomic binding energies. There are many similarities between atomic structure and nuclear structure, which will make our study of the properties of the nucleus somewhat easier. Nuclei are subject to the laws of quantum physics. They have ground and excited states and emit photons in transitions between the excited states. Just like atomic states, nuclear states can be labeled by their angular momentum. There are, however, two major differences between the study of atomic and nuclear properties. In atomic physics, the electrons experience the force provided by an external agent, the nucleus; in nuclear physics, there is no such external agent. In contrast to atomic physics, in which we can often consider the interactions among the electrons as a perturbation to the primary interaction between electrons and nucleus, in nuclear physics the mutual interaction of the nuclear constituents is just what provides the nuclear force, so we cannot treat this complicated many- body problem as a correction to a single-body problem.
    [Show full text]
  • R-Process Nucleosynthesis: on the Astrophysical Conditions
    r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalischer Modelle Zur Erlangung des Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim Tag der Einreichung: 07.02.2017, Tag der Prüfung: 29.05.2017 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Fachbereich Physik Institut für Kernphysik Theoretische Astrophysik r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalis- cher Modelle Genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Tag der Einreichung: 07.02.2017 Tag der Prüfung: 29.05.2017 Darmstadt 2017 — D 17 Bitte zitieren Sie dieses Dokument als: URN: urn:nbn:de:tuda-tuprints-63017 URL: http://tuprints.ulb.tu-darmstadt.de/6301 Dieses Dokument wird bereitgestellt von tuprints, E-Publishing-Service der TU Darmstadt http://tuprints.ulb.tu-darmstadt.de [email protected] Die Veröffentlichung steht unter folgender Creative Commons Lizenz: Namensnennung – Keine kommerzielle Nutzung – Keine Bearbeitung 4.0 International https://creativecommons.org/licenses/by-nc-nd/4.0/ Für meine Uroma Helene. Abstract The origin of the heaviest elements in our Universe is an unresolved mystery. We know that half of the elements heavier than iron are created by the rapid neutron capture process (r-process). The r-process requires an ex- tremely neutron-rich environment as well as an explosive scenario.
    [Show full text]
  • Final Excitation Energy of Fission Fragments
    Final excitation energy of fission fragments Karl-Heinz Schmidt and Beatriz Jurado CENBG, CNRS/IN2P3, Chemin du Solarium, B. P. 120, 33175 Gradignan, France Abstract: We study how the excitation energy of the fully accelerated fission fragments is built up. It is stressed that only the intrinsic excitation energy available before scission can be exchanged between the fission fragments to achieve thermal equilibrium. This is in contradiction with most models used to calculate prompt neutron emission where it is assumed that the total excitation energy of the final fragments is shared between the fragments by the condition of equal temperatures. We also study the intrinsic excitation- energy partition according to a level density description with a transition from a constant- temperature regime to a Fermi-gas regime. Complete or partial excitation-energy sorting is found at energies well above the transition energy. PACS: 24.75.+i, 24.60.Dr, 21.10.Ma Introduction: The final excitation energy found in the fission fragments, that is, the excitation energy of the fully accelerated fission fragments, and in particular its variation with the fragment mass, provides fundamental information on the fission process as it is influenced by the dynamical evolution of the fissioning system from saddle to scission and by the scission configuration, namely the deformation of the nascent fragments. The final fission-fragment excitation energy determines the number of prompt neutrons and gamma rays emitted. Therefore, this quantity is also of great importance for applications in nuclear technology. To properly calculate the value of the final excitation energy and its partition between the fragments one has to understand the mechanisms that lead to it.
    [Show full text]
  • Semi-Empirical Mass Formula 3.3 4.6 7.2 Ch 4
    Lecture 3 Krane Enge Cohen Willaims NUCLEAR PROPERTIES 1 Binding energy and stability Semi-empirical mass formula 3.3 4.6 7.2 Ch 4 2 Nuclear Spin 3.4 1.5 1.6 8.6 3 Magnetic dipole moment 3.5 1.7 1.6 8.7 4 Shape Electric Quadrupole moment 3.5 1.8 1.6 3.9, 8.8 Problems 1 From the table of nuclear masses given in the text, calculate the binding energy B, and B/A for 116Sn. 2 Calculate the various terms in the expression for the SEMF for 116Sn. From them determine B, B/A, and the mass. Compare the results with the values you obtained in question 1. 3 Using the details in the attached sheet, which is copied from Krane pages 70-72, confirm that 125Te is the most stable isobar with A=127. Also calculate the BE for both 127Te and 127I. , and thereby the energy of the β-decay. Is the β-decay β+ or β-? 4 Suppose the proton magnetic dipole moment were to be interpreted as due to the rotation of a positive uniform charge distribution of radius R, spinning about its axis with angular vel ω. a. By integrating over the charge distribution show that µ= eωR2/5 b. Using the classical relation for AM and ω, show that ωR2 = s/0.4 m2 c. Show that µ= (e/ 2m)s (analogous to Krane equ 3.32 µ= (e/ 2m)l 5. Calculate the electric quadrupole moment of a charge of magnitude Ze distributed over a ring of radius R with the axis along (a) the z-axis (b) the x-axis Tutorial Tuesday lunchtime room 210 on podium 15 Lecture 2 Review 1.
    [Show full text]
  • Nuclear Reaction Rates
    9 – Nuclear reaction rates introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 1 9.1 – Nuclear decays: Neutron decay By increasing the neutron number, the gain in binding energy of a nucleus due to the volume term is exceeded by the loss due to the growing asymmetry term. After that, no more neutrons can be bound, the neutron drip line is reached beyond which, neutron decay occurs: (Z, N) à (Z, N - 1) + n (9.1) Q-value: Qn = m(Z, N) - m(Z, N-1) - mn (9.2) Neutron Separation Energy Sn Sn(Z, N) = m(Z, N-1) + mn - m(Z, N) = -Qn for n-decay (9.3) Neutron drip line: Sn = 0 Beyond the drip line Sn < 0 neutron unbound Gamma-decay • When a reaction places a nucleus in an excited state, it drops to the lowest energy through gamma emission • Excited states and decays in nuclei are similar to atoms: (a) they conserve angular momentum and parity, (b) the photon has spin = 1 and parity = -1 • For orbital with angular momentum L, parity is given by P= (-1)L • To first order, the photon carries away the energy from an electric dipole transition in nuclei. But in nuclei it is easier to have higher order terms in than in atoms. introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 2 Proton decay Proton Separation Energy Sp: Sp(Z,N) = m(Z-1,N) + mp - m(Z,N) (9.4) Proton drip line: Sp = 0 beyond the drip line: Sp < 0 the nuclei are proton unbound α-decay α-decay is the emission of an a particle ( = 4He nucleus) The Q-value for a decay is given by Q "m(Z,A) m(Z 2,A 4) m $c2 α = # − − − − α % (9.5) Decay lifetimes Nuclear lifetimes for decay through all the modes described so far depend not only on the Q-values, but also on the conservation of other physical quantities, such as angular momentum.
    [Show full text]
  • Handbook for Calculations of Nuclear Reaction Data, RIPL-2 Reference Input Parameter Library-2
    IAEA-TECDOC-1506 Handbook for calculations of nuclear reaction data, RIPL-2 Reference Input Parameter Library-2 Final report of a coordinated research project August 2006 IAEA-TECDOC-1506 Handbook for calculations of nuclear reaction data, RIPL-2 Reference Input Parameter Library-2 Final report of a coordinated research project August 2006 The originating Section of this publication in the IAEA was: Nuclear Data Section International Atomic Energy Agency Wagramer Strasse 5 P.O. Box 100 A-1400 Vienna, Austria HANDBOOK FOR CALCULATIONS OF NUCLEAR REACTION DATA, RIPL-2 IAEA, VIENNA, 2006 IAEA-TECDOC-1506 ISBN 92–0–105206–5 ISSN 1011–4289 © IAEA, 2006 Printed by the IAEA in Austria August 2006 FOREWORD Nuclear data for applications constitute an integral part of the IAEA programme of ac- tivities. When considering low-energy nuclear reactions induced with light particles, such as neutrons, protons, deuterons, alphas and photons, a broad range of applications are addressed, from nuclear power reactors and shielding design through cyclotron production of medical radioisotopes and radiotherapy to transmutation of nuclear waste. All these and many other applications require a detailed knowledge of production cross sections, spectra of emitted particles and their angular distributions. A long-standing problem of how to meet the nuclear data needs of the future with limited experimental resources puts a considerable demand upon nuclear model compu- tation capabilities. Originally, almost all nuclear data were provided by measurement programmes. Over time, theoretical understanding of nuclear phenomena has reached a high degree of reliability, and nuclear modeling has become standard practice in nuclear data evaluations (with measurements remaining critical for data testing and benchmark- ing).
    [Show full text]
  • Nuclear Physics and Astrophysics SPA5302, 2019 Chris Clarkson, School of Physics & Astronomy [email protected]
    Nuclear Physics and Astrophysics SPA5302, 2019 Chris Clarkson, School of Physics & Astronomy [email protected] These notes are evolving, so please let me know of any typos, factual errors etc. They will be updated weekly on QM+ (and may include updates to early parts we have already covered). Note that material in purple ‘Digression’ boxes is not examinable. Updated 16:29, on 05/12/2019. Contents 1 Basic Nuclear Properties4 1.1 Length Scales, Units and Dimensions............................7 2 Nuclear Properties and Models8 2.1 Nuclear Radius and Distribution of Nucleons.......................8 2.1.1 Scattering Cross Section............................... 12 2.1.2 Matter Distribution................................. 18 2.2 Nuclear Binding Energy................................... 20 2.3 The Nuclear Force....................................... 24 2.4 The Liquid Drop Model and the Semi-Empirical Mass Formula............ 26 2.5 The Shell Model........................................ 33 2.5.1 Nuclei Configurations................................ 44 3 Radioactive Decay and Nuclear Instability 48 3.1 Radioactive Decay...................................... 49 CONTENTS CONTENTS 3.2 a Decay............................................. 56 3.2.1 Decay Mechanism and a calculation of t1/2(Q) .................. 58 3.3 b-Decay............................................. 62 3.3.1 The Valley of Stability................................ 64 3.3.2 Neutrinos, Leptons and Weak Force........................ 68 3.4 g-Decay...........................................
    [Show full text]
  • Magic Numbers Nucleon Separation Energies
    Magic numbers Experimental evidence for nuclear shell structure: + proton & neutron separation energies show similar behaviour to atomic ionization energies ( Fig. 5.1 & 5.2) Smooth increases correspond to filling of shell; sudden jumps indicate transitions to next shell. + Neutron capture probability drops drastically for nuclei with N =..., 50, 82, 126 ( Fig. 5.3b) Magic numbers of nucleons: nuclei with Z or N = 2, 8, 20, 28, 50, 82, 126 are extremely stable. Nuclei with Z and N magic numbers are said to be doubly magic e.g., 78Ni. P. Teixeira-Dias PH2510 - Atomic and Nuclear Physics Royal Holloway Univ of London Nucleon separation energies Compare ionization energies in atoms... ...with n/p separation energies in nucleii: c KS Krane Figure 5.1 c KS Krane Figure 5.2 P. Teixeira-Dias PH2510 - Atomic and Nuclear Physics Royal Holloway Univ of London The nuclear shell model (I) Neutron capture probability + Try to account for the observed magic numbers: . The harmonic oscillator potential and the infinite square well potential manage to reproduce some of these magic numbers... but not all: c KS Krane Figure 5.3 Figure 1: Shell strucyure obtained with infinite well and harmonic oscillator potentials. The capacity of each level is + marked drop in neutron capture probability for indicated to its right. Large gaps occur between levels, which we associate with closed shells. The circled numbers indicate the total nuclei with N = 28, 50, 82, 126 number of nucleons at each shell closure. c KS Krane, Figure 5.4 P. Teixeira-Dias PH2510 - Atomic and Nuclear Physics Royal Holloway Univ of London P.
    [Show full text]
  • Nuclear Binding Energy 1 Nuclear Binding Energy
    Nuclear binding energy 1 Nuclear binding energy Nuclear binding energy is the energy required to split a nucleus of an atom into its component parts. The component parts are neutrons and protons, which are collectively called nucleons. The binding energy of nuclei is always a positive number, since all nuclei require net energy to separate them into individual protons and neutrons. Thus, the mass of an atom's nucleus is always less than the sum of the individual masses of the constituent protons and neutrons when separated. This notable difference is a measure of the nuclear binding energy, which is a result of forces that hold the nucleus together. Because these forces result in the removal of energy when the nucleus is formed, and this energy has mass, mass is removed from the total mass of the original particles, and the mass is missing in the resulting nucleus. This missing mass is known as the mass defect, and represents the energy released when the nucleus is formed. Nuclear binding energy can also apply to situations when the nucleus splits into fragments composed of more than one nucleon, and in this case the binding energies for the fragments (as compared to the whole) may be either positive or negative, depending on where the parent nucleus and the daughter fragments fall on the nuclear binding energy curve (see below). If new binding energy is available when light nuclei fuse, or when heavy nuclei split, either of these processes result releases the binding energy. This energy—available as nuclear energy—can be used to produce nuclear power or build nuclear weapons.
    [Show full text]
  • Nuclear and Nuclear Excitation Energies
    ANTIBES (France ) 20 - 25 JUNE, 1994 NUCLEAR AND NUCLEAR EXCITATION ENERGIES ' ~ 9£»г* Sponsored by : CNRS/IN2P3 cl Laboratoires CEA/DAM - CEA/DSM IUR1SYS MESURES Résumés des contributions Abstracts of contributed papers ;.%•• I tpîi^ I •3' ï^^rrfV-- ^^?sji;>4.ô <,!!•*• ANTIBES, France June 20-25,1994 NUCLEAR SHAPES AND NUCLEAR STRUCTURE AT LOW EXCITATION ENERGIES Abstracts of contributed papers Résumés des contributions Edited by F. DYKSTRA, D. GOUTTE, J. SAUVAGE and M. VERGNES Institut de Physique Nucléaire F-91406 ORSAY Cedex France This volume has been prepared by Miss C. Vogelaer Ce fascicule a été préparé par Mette C. Vogelaer International Committee Comité International M. ARNOULD (Bruxelles) J. AYSTO (Jyvâskylà) J. BAUCHE (Orsay) D. BES (Buenos Aires) P. BONCHE (Saclay) H. BORNER (Grenoble) R.F. CASTEN (Brookhaven) H. DOUBRE (Orsay) D. HABS (Heidelberg) I. HAMAMOTO (Lwid; K. HEYDE (Gent) R.V.F. JANSSENS (Argonne) B. JONSON (Gôteborg) W. NAZAREWICZ (ORNL/Warsaw) E.W. OTTEN (Mamzj P. RING (Garching) H. SERGOLLE (Огаг^ P. Von BRENTANO (Ко/и) M. WEISS (Livermore) Organizing Committee Comité d'Organisation G. BARREAU (Bordeaux) J.-F. BERGER (Bruyères-le-Châtel) A. GIZON (Grenoble) D. GOUTTE (Saclay) P.H. HEENEN (Bruxelles) J. LIBERT (Orsay) M. MEYER 6Ly0rt) J. PINARD (Orsay) P. QUENTIN (Bordeaux) B. ROUSSIERE (Orjoy) J. SAUVAGE (Orsay) N. SCHULZ (Strasbourg) M. VERGNES Conférence Secrétariat Secrétariat de la Conférence F. DYKSTRA (Orsay) 232 CONTENTS - On the existence of intrinsic reflection asymmetry in Z~62, N~90 region 1 A.V. Afanasjev. S. Mizutori, I. Ragnarsson - Symmetry breaking in simple one and two level models 2 P.
    [Show full text]