DOCSLIB.ORG

Nuclear Reaction Rates

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

9 – Nuclear reaction rates introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 1 9.1 – Nuclear decays: Neutron decay By increasing the neutron number, the gain in binding energy of a nucleus due to the volume term is exceeded by the loss due to the growing asymmetry term. After that, no more neutrons can be bound, the neutron drip line is reached beyond which, neutron decay occurs: (Z, N) à (Z, N - 1) + n (9.1) Q-value: Qn = m(Z, N) - m(Z, N-1) - mn (9.2) Neutron Separation Energy Sn Sn(Z, N) = m(Z, N-1) + mn - m(Z, N) = -Qn for n-decay (9.3) Neutron drip line: Sn = 0 Beyond the drip line Sn < 0 neutron unbound Gamma-decay • When a reaction places a nucleus in an excited state, it drops to the lowest energy through gamma emission • Excited states and decays in nuclei are similar to atoms: (a) they conserve angular momentum and parity, (b) the photon has spin = 1 and parity = -1 • For orbital with angular momentum L, parity is given by P= (-1)L • To first order, the photon carries away the energy from an electric dipole transition in nuclei. But in nuclei it is easier to have higher order terms in than in atoms. introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 2 Proton decay Proton Separation Energy Sp: Sp(Z,N) = m(Z-1,N) + mp - m(Z,N) (9.4) Proton drip line: Sp = 0 beyond the drip line: Sp < 0 the nuclei are proton unbound α-decay α-decay is the emission of an a particle ( = 4He nucleus) The Q-value for a decay is given by Q "m(Z,A) m(Z 2,A 4) m $c2 α = # − − − − α % (9.5) Decay lifetimes Nuclear lifetimes for decay through all the modes described so far depend not only on the Q-values, but also on the conservation of other physical quantities, such as angular momentum. Typical decay times for similar lifetimes are (a) 10-10 s for beta decay, (b) 10-16 s for gamma-decay and (c) up to many years for alpha- decay. introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 3 Fission Very heavy nuclei can fission into two parts (Q > 0) This happens because for large nuclei the surface energy is less important – large deformations are then possible. With a small amount of additional energy the nucleus can be deformed sufficiently so that Coulomb repulsion wins over nucleon-nucleon attraction and the nucleus fissions. This will be possible if Q "m(Z,A) 2m(Z / 2,A / 2)$c2 0 (9.6) f = # − % > Ma ss Num ber A Using the LDM formula, Eq. 80 100 120 140 160 20 (7.5) we can shown that Qα > 0 this happens Nuc lear C harge Yield in Fission of 234U for A > 90. 15 ) % ( Symmetric fission (fission into ) Z 10 two nearly equal size fragments) ( Y d as well as asymmetric fission are l e i likely to occur. Y 5 0 Example from 25 30 35 40 45 50 55 60 65 Moller et al., Nature 409 (2001) 485 Proton Num b e r Z introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 4 4 9.2 - Observations 1. Most nuclei found in nature are the stable and not too heavy to undergo alpha decay or fission) 2. There are many more unstable nuclei that can exist for short times after their creation. 3. Alpha particle is favored building blocks of nuclei because of their comparably low Coulomb barrier when fused with other nuclei high binding energy per nucleon This explains abundance peaks at nuclei composed of multiples of alpha particles in solar system abundance distribution 4. The binding energy per nucleon has a maximum in the Iron-Nickel region The iron peak in solar abundance distribution implies that some fraction of matter was brought into equilibrium, probably during supernovae explosions. introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 5 Observations – Solar abundances introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 6 9.3 - Nuclear reactions in stars The plasma within a star is a mix of fully ionized projectiles and target nuclei at a temperature T. Using the definition of cross section in Eq. (7.24), we get that for particles with a given relative velocity v and within a volume V with projectile number density ni, and target number density nj: λ = σ n v i (9.7) R = σ nivn jV 3 so for reaction rate per second and cm is (9.8) r = nin jσ v This is proportional to the number of i-j pairs in the volume. However, when the species are identical, i.i., i =j, one has to divide by 2 to avoid double counting 1 r = n n σ v 1 i j (9.9) +δij introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 7 Reaction rates at temperature T Assuming Local Thermal Equilibrium LTE the velocity distribution of particles in a plasma follow a Maxwell-Boltzmann velocity distribution: 3/ 2 mv2 ⎛ m ⎞ − 2 2kT (9.10) with Φ(v)dv =1 (9.11) Φ(v) = 4π ⎜ ⎟ v e ∫ ⎝ 2π kT ⎠ where Φ(v) is the probability to find a particle with a velocity between v and v + dv. This distribution is easily deduced from the Boltzmann distribution f(E) = A exp(-E/kT) by replacing E = mv2/2 and adjusting the constant A to conform with the max at normalization condition E = kT given by Eq. (9.11). introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 8 Reaction rates at temperature T In terms of the Maxwell-Boltzmann distribution, with the mass m replaced by the reduced mass m of the i and j particles, i.e., m m 3/ 2 µ v2 i j − µ = (9.12) ⎛ µ ⎞ 2 2kT (9.13) m m Φ(v) = 4π ⎜ ⎟ v e i + j ⎜ ⎟ ⎝ 2π kT ⎠ In the stellar environments, the reaction rates given in Eq. (9.9) has to be averaged over velocities, 1 r = nin j < σ v > (9.14) 1+δij using over the distribution Φ(v), 1 r n n (v) (v)vdv (9.15) = i j ∫ σ Φ 1+δij introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 9 Reaction rates in terms of abundances 3 In terms of units of stellar reaction rate given by NA<σv> in cm /s/g, the reaction rate per second and per cm3, is 1 2 2 (9.16) r = YiYjρ NA < σ v > 1+δij Sometimes, one uses another notation for reactions per second and target nucleus j, by dividing the above equation by YjρNA, i.e., 1 One usually call this by the λ = Yiρ NA < σ v > (9.17) stellar reaction rate of a 1+δij specific reaction As an application, lets assume that the species i and j are destructed by j capturing the projectile i in the form i + j à k. Then dn j = −n λ = −n Y ρ N < σ v > dt j j i A (9.18) dn k = n λ dt k introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 10 Reaction rates in terms of abundances Since the dnj/dt is proportional to –nj, the solution of the equation is a decaying exponential. And since the species k is built from the destruction of of j, its time dependence should be proportional to [1 – nj(t)]. In other words, n (t) = n e−λ t j 0 j (9.19) −λ t n k (t) = n0k (1− e ) In terms of the abundances: Y (t) = Y e−λ t j 0 j (9.20) −λ t Yk (t) = Y0k (1− e ) The lifetime for the destruction of j is 1 1 τ = = (9.21) λ Yjρ NA < σ v > After a time equal to a few multiples of τ, the species j is almost completely destroyed while k is almost completely built up from i and j capture. One often uses the name “half-life”, τ1/2, instead of lifetime, where τ1/2 = τ ln2. introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 11 9.4 - Energy generation Lets consider the energy generation by nuclear reaction sin stars. As we know the energy released is given by the Q-values ⎛ ⎞ Q c2 ⎜ m m ⎟ (9.22) = ⎜ ∑ i − ∑ j ⎟ ⎝ initial nuclei i final nuclei j ⎠ where m are the respective masses of the particles. The energy generated per gram and second by a reaction i + j is then rQ 1 2 ε = = Q YiYjρNA < σ v > (9.23) ρ 1+δij We can now define the reaction flow as the abundance of nuclei converted in time T from species j to k via a specific reaction as T !dY $ T F = dt# j & = λ(t)Y (t)dt ∫ # dt & ∫ j (9.24) 0 " %via specific reaction 0 introduc)on to Astrophysics, C. Bertulani, Texas A&M-Commerce 12 Branching Consider possibilities as in the figure on the side in terms k of several possible reaction rates λi i j The total destruction rate for the nucleus is m λ = ∑λi (9.25) i And its total lifetime is given by 1 1 τ = = (9.26) λ ∑λi i The reaction flow branching into reaction i, bi is the fraction of destructive flow through reaction i. (or the fraction of nuclei destroyed via reaction i) λi bi = (9.27) ∑λ j j introduc)on to Astrophysics, C.
Recommended publications
  • Arxiv:1904.10318V1 [Nucl-Th] 20 Apr 2019 Ucinltheory

    Arxiv:1904.10318V1 [Nucl-Th] 20 Apr 2019 Ucinltheory

    Nuclear structure investigation of even-even Sn isotopes within the covariant density functional theory Y. EL BASSEM1, M. OULNE2 High Energy Physics and Astrophysics Laboratory, Department of Physics, Faculty of Sciences SEMLALIA, Cadi Ayyad University, P.O.B. 2390, Marrakesh, Morocco. Abstract The current investigation aims to study the ground-state properties of one of the most interesting isotopic chains in the periodic table, 94−168Sn, from the proton drip line to the neutron drip line by using the covariant density functional theory, which is a modern theoretical tool for the description of nuclear structure phenomena. The physical observables of interest include the binding energy, separation energy, two-neutron shell gap, rms-radii for protons and neutrons, pairing energy and quadrupole deformation. The calculations are performed for a wide range of neutron numbers, starting from the proton-rich side up to the neutron-rich one, by using the density- dependent meson-exchange and the density dependent point-coupling effec- tive interactions. The obtained results are discussed and compared with available experimental data and with the already existing results of rela- tivistic Mean Field (RMF) model with NL3 functional. The shape phase transition for Sn isotopic chain is also investigated. A reasonable agreement is found between our calculated results and the available experimental data. Keywords: Ground-state properties, Sn isotopes, covariant density functional theory. arXiv:1904.10318v1 [nucl-th] 20 Apr 2019 1. INTRODUCTION In nuclear
  • Uranium (Nuclear)

    Uranium (Nuclear)

    Uranium (Nuclear) Uranium at a Glance, 2016 Classification: Major Uses: What Is Uranium? nonrenewable electricity Uranium is a naturally occurring radioactive element, that is very hard U.S. Energy Consumption: U.S. Energy Production: and heavy and is classified as a metal. It is also one of the few elements 8.427 Q 8.427 Q that is easily fissioned. It is the fuel used by nuclear power plants. 8.65% 10.01% Uranium was formed when the Earth was created and is found in rocks all over the world. Rocks that contain a lot of uranium are called uranium Lighter Atom Splits Element ore, or pitch-blende. Uranium, although abundant, is a nonrenewable energy source. Neutron Uranium Three isotopes of uranium are found in nature, uranium-234, 235 + Energy FISSION Neutron uranium-235, and uranium-238. These numbers refer to the number of Neutron neutrons and protons in each atom. Uranium-235 is the form commonly Lighter used for energy production because, unlike the other isotopes, the Element nucleus splits easily when bombarded by a neutron. During fission, the uranium-235 atom absorbs a bombarding neutron, causing its nucleus to split apart into two atoms of lighter mass. The first nuclear power plant came online in Shippingport, PA in 1957. At the same time, the fission reaction releases thermal and radiant Since then, the industry has experienced dramatic shifts in fortune. energy, as well as releasing more neutrons. The newly released neutrons Through the mid 1960s, government and industry experimented with go on to bombard other uranium atoms, and the process repeats itself demonstration and small commercial plants.
  • An Introduction to the IAEA Neutron-Gamma Atlas Ye Myint1, Sein Htoon2

    An Introduction to the IAEA Neutron-Gamma Atlas Ye Myint1, Sein Htoon2

    MM0900107 Jour. Myan. Aca<L Arts & Sa 2005 Vol. in. No. 3(i) Physics An Introduction to the IAEA Neutron-Gamma Atlas Ye Myint1, Sein Htoon2 Abstract NG-ATLAS is the abbreviation of Neutron-Gamma Atlas. Neutrons have proved to be especially effective in producing nuclear transformations, and gamma is the informer of nucleus. In nuclear physics, observable features or data are determined externally such as, energy, spin and cross section, where neutron and gamma plays dominant roles. (Neutron, gamma) (n,y) reactions of every isotope are vital importance for nuclear physicists. Introduction Inside the nucleus, protons and neutrons are simply two different states of a single particle, the nucleon. When neutron leaves the.nucleus, it is an unstable particle of half life 11.8 minutes, beta decay into proton. It is not feasible to describe beta decay without the references to Dirac 's hole theory; it is the memorandum for his hundred-birth day . The role of neutrons in nuclear physics is so high and its radiative capture by elements (neutron, gamma) reaction i.e, (n,y ) or NG-ATLAS is presented. The NG-Atlas. data file contains nuclear reaction cross section data of induced capture reaction for targets up to Z =96 . It comprises more than seven hundred isotopes, if the half lives are above half of a day. Cross sections are listed separately for ground , first and second excited states .And if the isomers have half life longer than 0.5 days , they are also include as targets .So the information includes a total of about one thousand reactions on different channels and the incident neutron energy ranging fromlO"5 eV to 20 MeV.
  • Range of Usefulness of Bethe's Semiempirical Nuclear Mass Formula

    Range of Usefulness of Bethe's Semiempirical Nuclear Mass Formula

    RANGE OF ..USEFULNESS OF BETHE' S SEMIEMPIRIC~L NUCLEAR MASS FORMULA by SEKYU OBH A THESIS submitted to OREGON STATE COLLEGE in partial fulfillment or the requirements tor the degree of MASTER OF SCIENCE June 1956 TTPBOTTDI Redacted for Privacy lrrt rtllrt ?rsfirror of finrrtor Ia Ohrr;r ef lrJer Redacted for Privacy Redacted for Privacy 0hrtrurn of tohoot Om0qat OEt ttm Redacted for Privacy Dru of 0rrdnrtr Sohdbl Drta thrrlr tr prrrEtrl %.ifh , 1,,r, ," r*(,-. ttpo{ by Brtty Drvlr ACKNOWLEDGMENT The author wishes to express his sincere appreciation to Dr. G. L. Trigg for his assistance and encouragement, without which this study would not have been concluded. The author also wishes to thank Dr. E. A. Yunker for making facilities available for these calculations• • TABLE OF CONTENTS Page INTRODUCTION 1 NUCLEAR BINDING ENERGIES AND 5 SEMIEMPIRICAL MASS FORMULA RESEARCH PROCEDURE 11 RESULTS 17 CONCLUSION 21 DATA 29 f BIBLIOGRAPHY 37 RANGE OF USEFULNESS OF BETHE'S SEMIEMPIRICAL NUCLEAR MASS FORMULA INTRODUCTION The complicated experimental results on atomic nuclei haYe been defying definite interpretation of the structure of atomic nuclei for a long tfme. Even though Yarious theoretical methods have been suggested, based upon the particular aspects of experimental results, it has been impossible to find a successful theory which suffices to explain the whole observed properties of atomic nuclei. In 1936, Bohr (J, P• 344) proposed the liquid drop model of atomic nuclei to explain the resonance capture process or nuclear reactions. The experimental evidences which support the liquid drop model are as follows: 1. Substantially constant density of nuclei with radius R - R Al/3 - 0 (1) where A is the mass number of the nucleus and R is the constant of proportionality 0 with the value of (1.5! 0.1) x 10-lJcm~ 2.
  • Fundamentals of Nuclear Power

    Fundamentals of Nuclear Power

    Fundamentals of Nuclear Power Juan S. Giraldo Douglas J. Gotham David G. Nderitu Paul V. Preckel Darla J. Mize State Utility Forecasting Group December 2012 Table of Contents List of Figures .................................................................................................................................. iii List of Tables ................................................................................................................................... iv Acronyms and Abbreviations ........................................................................................................... v Glossary ........................................................................................................................................... vi Foreword ........................................................................................................................................ vii 1. Overview ............................................................................................................................. 1 1.1 Current state of nuclear power generation in the U.S. ......................................... 1 1.2 Nuclear power around the world ........................................................................... 4 2. Nuclear Energy .................................................................................................................... 9 2.1 How nuclear power plants generate electricity ..................................................... 9 2.2 Radioactive decay .................................................................................................
  • Nuclear Chemistry Why? Nuclear Chemistry Is the Subdiscipline of Chemistry That Is Concerned with Changes in the Nucleus of Elements

    Nuclear Chemistry Why? Nuclear Chemistry Is the Subdiscipline of Chemistry That Is Concerned with Changes in the Nucleus of Elements

    Nuclear Chemistry Why? Nuclear chemistry is the subdiscipline of chemistry that is concerned with changes in the nucleus of elements. These changes are the source of radioactivity and nuclear power. Since radioactivity is associated with nuclear power generation, the concomitant disposal of radioactive waste, and some medical procedures, everyone should have a fundamental understanding of radioactivity and nuclear transformations in order to evaluate and discuss these issues intelligently and objectively. Learning Objectives λ Identify how the concentration of radioactive material changes with time. λ Determine nuclear binding energies and the amount of energy released in a nuclear reaction. Success Criteria λ Determine the amount of radioactive material remaining after some period of time. λ Correctly use the relationship between energy and mass to calculate nuclear binding energies and the energy released in nuclear reactions. Resources Chemistry Matter and Change pp. 804-834 Chemistry the Central Science p 831-859 Prerequisites atoms and isotopes New Concepts nuclide, nucleon, radioactivity, α− β− γ−radiation, nuclear reaction equation, daughter nucleus, electron capture, positron, fission, fusion, rate of decay, decay constant, half-life, carbon-14 dating, nuclear binding energy Radioactivity Nucleons two subatomic particles that reside in the nucleus known as protons and neutrons Isotopes Differ in number of neutrons only. They are distinguished by their mass numbers. 233 92U Is Uranium with an atomic mass of 233 and atomic number of 92. The number of neutrons is found by subtraction of the two numbers nuclide applies to a nucleus with a specified number of protons and neutrons. Nuclei that are radioactive are radionuclides and the atoms containing these nuclei are radioisotopes.
  • Nuclear Reactions Fission Fusion

    Nuclear Reactions Fission Fusion

    Nuclear Reactions Fission Fusion Nuclear Reactions and the Transmutation of Elements A nuclear reaction takes place when a nucleus is struck by another nucleus or particle. Compare with chemical reactions ! If the original nucleus is transformed into another, this is called transmutation. a-induced Atmospheric reaction. 14 14 n-induced n 7N 6C p Deuterium production reaction. 16 15 2 n 8O 7 N 1H Note: natural “artificial” radioactivity Nuclear Reactions and the Transmutation of Elements Energy and momentum must be conserved in nuclear reactions. Generic reaction: The reaction energy, or Q-value, is the sum of the initial masses less the sum of the final masses, multiplied by c2: If Q is positive, the reaction is exothermic, and will occur no matter how small the initial kinetic energy is. If Q is negative, there is a minimum initial kinetic energy that must be available before the reaction can take place (endothermic). Chemistry: Arrhenius behaviour (barriers to reaction) Nuclear Reactions and the Transmutation of Elements A slow neutron reaction: is observed to occur even when very slow-moving neutrons (mass Mn = 1.0087 u) strike a boron atom at rest. 6 Analyze this problem for: vHe=9.30 x 10 m/s; Calculate the energy release Q-factor This energy must be liberated from the reactants. (verify that this is possible from the mass equations) Nuclear Reactions and the Transmutation of Elements Will the reaction “go”? Left: M(13-C) = 13.003355 Right: M(13-N) = 13.005739 M(1-H) = 1.007825 + M(n) = 14.014404 D(R-L)= 0.003224 u (931.5 MeV/u) = +3.00 MeV (endothermic) Hence bombarding by 2.0-MeV protons is insufficient 3.0 MeV is required since Q=-3.0 MeV (actually a bit more; for momentum conservation) Nuclear Reactions and the Transmutation of Elements Neutrons are very effective in nuclear reactions, as they have no charge and therefore are not repelled by the nucleus.
  • Chapter 14 NUCLEAR FUSION

    Chapter 14 NUCLEAR FUSION

    Chapter 14 NUCLEAR FUSION For the longer term, the National Energy Strategy looks to fusion energy as an important source of electricity-generating capacity. The Department of Energy will continue to pursue safe and environmentally sound approaches to fusion energy, pursuing both the magnetic confinement and the inertial confinement concepts for the foreseeable future. International collaboration will become an even more important element of the magnetic fusion energy program and will be incorporated into the inertial fusion energy program to the fullest practical extent. (National Energy Strategy, Executive Summary, 1991/1992) Research into fundamentally new, advanced energy sources such as [...] fusion energy can have substantial future payoffs... [T]he Nation's fusion program has made steady progress and last year set a record of producing 10.7 megawatts of power output at a test reactor supported by the Department of Energy. This development has significantly enhanced the prospects for demonstrating the scientific feasibility of fusion power, moving us one step closer to making this energy source available sometime in the next century. (Sustainable Energy Strategy, 1995) 258 CHAPTER 14 Nuclear fusion is essentially the antithesis of the fission process. Light nuclei are combined in order to release excess binding energy and they form a heavier nucleus. Fusion reactions are responsible for the energy of the sun. They have also been used on earth for uncontrolled release of large quantities of energy in the thermonuclear or ‘hydrogen’ bombs. However, at the present time, peaceful commercial applications of fusion reactions do not exist. The enormous potential and the problems associated with controlled use of this essentially nondepletable energy source are discussed briefly in this chapter.
  • 16. Fission and Fusion Particle and Nuclear Physics

    16. Fission and Fusion Particle and Nuclear Physics

    16. Fission and Fusion Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 16. Fission and Fusion 1 In this section... Fission Reactors Fusion Nucleosynthesis Solar neutrinos Dr. Tina Potter 16. Fission and Fusion 2 Fission and Fusion Most stable form of matter at A~60 Fission occurs because the total Fusion occurs because the two Fission low A nuclei have too large a Coulomb repulsion energy of p's in a surface area for their volume. nucleus is reduced if the nucleus The surface area decreases Fusion splits into two smaller nuclei. when they amalgamate. The nuclear surface The Coulomb energy increases, energy increases but its influence in the process, is smaller. but its effect is smaller. Expect a large amount of energy released in the fission of a heavy nucleus into two medium-sized nuclei or in the fusion of two light nuclei into a single medium nucleus. a Z 2 (N − Z)2 SEMF B(A; Z) = a A − a A2=3 − c − a + δ(A) V S A1=3 A A Dr. Tina Potter 16. Fission and Fusion 3 Spontaneous Fission Expect spontaneous fission to occur if energy released E0 = B(A1; Z1) + B(A2; Z2) − B(A; Z) > 0 Assume nucleus divides as A , Z A1 Z1 A2 Z2 1 1 where = = y and = = 1 − y A, Z A Z A Z A2, Z2 2 2=3 2=3 2=3 Z 5=3 5=3 from SEMF E0 = aSA (1 − y − (1 − y) ) + aC (1 − y − (1 − y) ) A1=3 @E0 maximum energy released when @y = 0 @E 2 2 Z 2 5 5 0 = a A2=3(− y −1=3 + (1 − y)−1=3) + a (− y 2=3 + (1 − y)2=3) = 0 @y S 3 3 C A1=3 3 3 solution y = 1=2 ) Symmetric fission Z 2 2=3 max.
  • Modern Physics to Which He Did This Observation, Usually to Within About 0.1%

    Modern Physics to Which He Did This Observation, Usually to Within About 0.1%

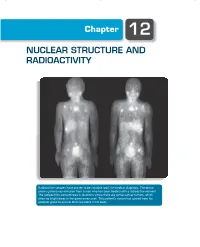
    Chapter 12 NUCLEAR STRUCTURE AND RADIOACTIVITY Radioactive isotopes have proven to be valuable tools for medical diagnosis. The photo shows gamma-ray emission from a man who has been treated with a radioactive element. The radioactivity concentrates in locations where there are active cancer tumors, which show as bright areas in the gamma-ray scan. This patient’s cancer has spread from his prostate gland to several other locations in his body. 370 Chapter 12 | Nuclear Structure and Radioactivity The nucleus lies at the center of the atom, occupying only 10−15 of its volume but providing the electrical force that holds the atom together. Within the nucleus there are Z positive charges. To keep these charges from flying apart, the nuclear force must supply an attraction that overcomes their electrical repulsion. This nuclear force is the strongest of the known forces; it provides nuclear binding energies that are millions of times stronger than atomic binding energies. There are many similarities between atomic structure and nuclear structure, which will make our study of the properties of the nucleus somewhat easier. Nuclei are subject to the laws of quantum physics. They have ground and excited states and emit photons in transitions between the excited states. Just like atomic states, nuclear states can be labeled by their angular momentum. There are, however, two major differences between the study of atomic and nuclear properties. In atomic physics, the electrons experience the force provided by an external agent, the nucleus; in nuclear physics, there is no such external agent. In contrast to atomic physics, in which we can often consider the interactions among the electrons as a perturbation to the primary interaction between electrons and nucleus, in nuclear physics the mutual interaction of the nuclear constituents is just what provides the nuclear force, so we cannot treat this complicated many- body problem as a correction to a single-body problem.
  • R-Process Nucleosynthesis: on the Astrophysical Conditions

    R-Process Nucleosynthesis: on the Astrophysical Conditions

    r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalischer Modelle Zur Erlangung des Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim Tag der Einreichung: 07.02.2017, Tag der Prüfung: 29.05.2017 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Fachbereich Physik Institut für Kernphysik Theoretische Astrophysik r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalis- cher Modelle Genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Tag der Einreichung: 07.02.2017 Tag der Prüfung: 29.05.2017 Darmstadt 2017 — D 17 Bitte zitieren Sie dieses Dokument als: URN: urn:nbn:de:tuda-tuprints-63017 URL: http://tuprints.ulb.tu-darmstadt.de/6301 Dieses Dokument wird bereitgestellt von tuprints, E-Publishing-Service der TU Darmstadt http://tuprints.ulb.tu-darmstadt.de [email protected] Die Veröffentlichung steht unter folgender Creative Commons Lizenz: Namensnennung – Keine kommerzielle Nutzung – Keine Bearbeitung 4.0 International https://creativecommons.org/licenses/by-nc-nd/4.0/ Für meine Uroma Helene. Abstract The origin of the heaviest elements in our Universe is an unresolved mystery. We know that half of the elements heavier than iron are created by the rapid neutron capture process (r-process). The r-process requires an ex- tremely neutron-rich environment as well as an explosive scenario.
  • Final Excitation Energy of Fission Fragments

    Final Excitation Energy of Fission Fragments

    Final excitation energy of fission fragments Karl-Heinz Schmidt and Beatriz Jurado CENBG, CNRS/IN2P3, Chemin du Solarium, B. P. 120, 33175 Gradignan, France Abstract: We study how the excitation energy of the fully accelerated fission fragments is built up. It is stressed that only the intrinsic excitation energy available before scission can be exchanged between the fission fragments to achieve thermal equilibrium. This is in contradiction with most models used to calculate prompt neutron emission where it is assumed that the total excitation energy of the final fragments is shared between the fragments by the condition of equal temperatures. We also study the intrinsic excitation- energy partition according to a level density description with a transition from a constant- temperature regime to a Fermi-gas regime. Complete or partial excitation-energy sorting is found at energies well above the transition energy. PACS: 24.75.+i, 24.60.Dr, 21.10.Ma Introduction: The final excitation energy found in the fission fragments, that is, the excitation energy of the fully accelerated fission fragments, and in particular its variation with the fragment mass, provides fundamental information on the fission process as it is influenced by the dynamical evolution of the fissioning system from saddle to scission and by the scission configuration, namely the deformation of the nascent fragments. The final fission-fragment excitation energy determines the number of prompt neutrons and gamma rays emitted. Therefore, this quantity is also of great importance for applications in nuclear technology. To properly calculate the value of the final excitation energy and its partition between the fragments one has to understand the mechanisms that lead to it.