DOCSLIB.ORG

Neutrino-Nucleon Deep Inelastic Scattering

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Neutrino-Nucleon Deep Inelastic Scattering ν NeutrinoNeutrino--NucleonNucleon DeepDeep InelasticInelastic ScatteringScattering 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 48 NeutrinoNeutrino--NucleonNucleon ‘‘nn aa NutshellNutshell ν • Charged - Current: W± exchange • Neutral - Current: Z0 exchange Quasi-elastic Scattering: Elastic Scattering: (Target changes but no break up) (Target unchanged) − νμ + n →μ + p νμ + N →νμ + N Nuclear Resonance Production: Nuclear Resonance Production: (Target goes to excited state) (Target goes to excited state) − 0 * * νμ + n →μ + p + π (N or Δ) νμ + N →νμ + N + π (N or Δ) n + π+ Deep-Inelastic Scattering: Deep-Inelastic Scattering (Nucleon broken up) (Nucleon broken up) − νμ + quark →μ + quark’ νμ + quark →νμ + quark Linear rise with energy Resonance Production 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 49 ν ScatteringScattering VariablesVariables Scattering variables given in terms of invariants •More general than just deep inelastic (neutrino-quark) scattering, although interpretation may change. 2 4-momentum Transfer22 : Qq=− 2 =− ppEE'' − ≈ 4 sin 2 (θ / 2) ( ) ( )Lab Energy Transfer: ν =⋅qP/ M = E − E' = E − M ()ThT()Lab ()Lab ' Inelasticity: yqPpPEM=⋅()()(/ ⋅ =hT − ) / EE h + ()Lab 22 Fractional Momentum of Struck Quark: xq=−/ 2() pqQM ⋅ = / 2 Tν 22 2 2 2 Recoil Mass : WqPM=+( ) =TT + 2 MQν − Q2 CM Energy222 : spPM=+( ) = + T xy 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 50 ν 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 51 ν PartonParton InterpretationInterpretation ofof DISDIS Mass of target quark 22222 mxPxMqT== μ ν Mass of final state quark 2 2 m q, = (xP + q) qp= ν − pμ In “infinite momentum frame”, x is momentum of partons inside the nucleon Q2 Q2 x = = Neutrino scatters off a 2P ⋅q 2M Tν parton inside the nucleon 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 52 SoSo whywhy isis crosscross--sectionsection soso ν large?large? • (at least compared to νe- scattering!) • Recall that for neutrino beam and target at rest 2 GGs22Qsmax ≡ σ ≈=FFdQ2 TOT ∫ π 0 π 2 sm=+ee2 mEν • But we just learned for DIS that effective mass of each target quark is mxmq = nucleon • So much larger target mass means larger σTOT 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 53 Chirality,Chirality, ChargeCharge inin CCCC νν--qq ν ScatteringScattering • Total spin determines * inelasticity distribution Flat in y Familiar from neutrino- electron scattering ♠ 1/4(1+cosθ∗)2 = (1-y)2 ν p 2 * ♠ ∫(1-y)2dy=1/3 dσ Gs 2 =+−F xd() x xu ()(1 x y ) • Neutrino/Anti-neutrino CC dxdy π () each produce particular Δq dσν p Gs2 * ♠ =+−F xd() x xu ()(1 x y )2 in scattering dxdy π () νd → μ −u νu → μ +d 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 54 ν FactorizationFactorization andand PartonsPartons • Factorization Theorem of QCD allows amplitudes for hadronic processes to be written as: A(l + h → l + X ) = dxA(l + q(x) → l + X )q (x) ∑∫ h q Parton distribution functions (PDFs) are universal Processes well described by single parton interactions Parton distribution functions not (yet) calculable from first principles in QCD • “Scaling”: parton distributions are largely independent of Q2 scale, and depend on fractional momentum, x. 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 55 ν 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 56 MomentumMomentum ofof QuarksQuarks && ν AntiquarksAntiquarks • Momentum carried by quarks much greater than anti-quarks in nucleon qx() qx() 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 57 yy distributiondistribution inin NeutrinoNeutrino CCCC ν DISDIS dqdqσ ()νσν ( ) =∝1 dxdy dxdy dqdqσν() σν () 2 y=0: 0.14 =∝−()1 y neutrino dxdy dxdy 0.12 Quarks & antineutrino anti-quarks 0.1 y=1: Neutrino and anti-neutrino 0.08 Neutrinos see identical only quarks. 0.06 Anti-neutrinos 0.04 see only anti- quarks 0.02 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 ν 1 ν σ ≈ 2 σ 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 58 TouchstoneTouchstone QuestionQuestion #4:#4: ν NeutrinoNeutrino andand AntiAnti--NeutrinoNeutrino σσνN ν 1 ν • Given: σσ CC ≈ 2 CC in the DIS regime (CC) dqdqσ ()νσνσνσν ( ) dq () dq () ==33 = and dx dx dx dx for CC scattering from quarks or anti-quarks of a given momentum, and that cross-section is proportional to parton momentum, what is the approximate ratio of anti- quark to quark momentum in the nucleon? (a) qq/~1/3 (b) qq/~1/5 (c) qq/~1/8 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 59 MomentumMomentum ofof QuarksQuarks && ν AntiquarksAntiquarks • Momentum carried by quarks much greater than anti-quarks qx()in nucleon Rule of thumb: at Q2 of 10 GeV2: total quark momentum is 1/3 qx() 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 62 StrongStrong InteractionsInteractions amongamong ν PartonsPartons Q2 Scaling fails due to these interactions ∂qxQ(, 2 ) α ()Qdy2 1 = s 2 ∫ ∂ logQ 2π x y ⎡ ⎛⎞xx2 ⎛⎞ 2 ⎤ ⎢Pqq⎜⎟qy(),Q + P qg ⎜⎟gyQ(, )⎥ ⎣ ⎝ yy⎠⎠⎝ ⎦ •Pqq(x/y) = probability of finding a quark with momentum x within a quark with momentum y •Pqq(x/y) = probability of finding a q with momentum x within a gluon with momentum y 41+ z2 Pz()=+− 2(1δ z ) qq 3(1− z ) 1 2 Pz()=+−⎡⎤ z2 () 1 z gq 2 ⎣⎦ 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 63 ν 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 64 ν ScalingScaling fromfrom QCDQCD Observed quark distributions vary with Q2 Scaling well modeled by perturbative QCD with a single free parameter (αs) 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 65 IfIf youyou findfind thisthis difficultdifficult toto ν rememberremember…… • It may help you to imagine scaling up a mountain • Perhaps after yesterday it is more intuitive that as you go up in scale the average momentum of each hiking group decreases and the number of hiking groups increases… 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 66 ν DIS:DIS: RelatingRelating SFsSFs toto PartonParton DistributionsDistributions 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 67 ν StructureStructure FunctionsFunctions (SFs)(SFs) • A model-independent picture of these interactions can also be formed in terms of nucleon “structure functions” All Lorentz-invariant terms included Approximate zero lepton mass (small correction) ν ,ν dσ ⎡ 2 2 ⎛ M T xy ⎞ 2 2 ⎤ ∝ ⎢y 2xF1(x,Q ) + ⎜2 − 2y − ⎟F2 (x,Q ) ± y()2 − y xF3 (x,Q )⎥ dxdy ⎣ ⎝ E ⎠ ⎦ • For massless free spin-1/2 partons, one simplification… Callan-Gross relationship, 2xF1=F2 Implies intermediate bosons are completely transverse Can parameterize transverse cross-section by RL. 2 2 σ L F2 ⎛ 4M T x ⎞ •Callan-Gross violations, M R = = ⎜1+ ⎟ L ⎜ 2 ⎟ •NLO pQCD, g → qq σ T 2xF1 ⎝ Q ⎠ 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 68 ν SFsSFs toto PDFsPDFs • Can relate SFs to PDFs in naïve quark-parton model by matching y dependence Assuming Callan-Gross, massless targets and partons… 2 2 2 2 F3: 2y-y =(1-y) -1 , 2xF1=F2: 2-2y+y =(1-y) +1 νp,CC 2xF1 = x[d p (x) + u p (x) + s p (x) + cp (x)] νp,CC xF3 = x[]d p (x) − u p (x) + s p (x) − c p (x) • In analogy with neutrino-electron scattering, CC only involves left-handed quarks • However, NC involves both chiralities (V-A and V+A) Also couplings from EW Unification And no selection by quark charge 2xFν pNC,22=+ xuuuxuxcxcx⎡ ( )()()()()( +++++ d 22 d )()()()() dxdxsxsx +++⎤ 1 ⎣ LRpppp() LRpppp( )⎦ xFν pNC,22=− xuuuxuxcxcx⎡( ) () −+−+− () () () ( d 22 d ) dxdxsxsx () −+− () () ()⎤ 3 ⎣ LRp() p p p L R() p p p p ⎦ 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 69 ν IsoscalarIsoscalar TargetsTargets • Heavy nuclei are roughly neutron-proton isoscalar • Isospin symmetry implies u p = dn ,d p = un • Structure Functions have a particularly simple interpretation in quark-parton model for this case… d 2()σ νν N Gs2 =+−±−−F 1(1)()1(1)yFx22() yxFxνν () dxdy 2π {}()()23 νν()NCC , 2xF1 () x=+++++++=+ xuxdxuxdxsxsxcxcxxqxxqx (() () () () () () () () () () νν()NCC , xF3 () x=+±− xuVal () x xd Val () x 2(() x s x c ()) x where uVal ( x )=− ux ( ) ux ( ) 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 70 ν NuclearNuclear EffectsEffects inin DISDIS • Well measured effects in charged-lepton DIS Maybe the same for neutrino DIS; maybe not… all precise neutrino data is on Ca or Fe targets! Conjecture: these can be absorbed into effective nucleon PDFs in a nucleus Anti-shadowing 0.001 0.01 0.1 1 2 3 4 5 6 7 2 3 4 5 6 7 2 3 4 5 6 7 1.1 1.1 shadowing Fermi 1.0 1.0 motion (D) 2 0.9 0.9 (X) / F 2 NMC Ca/D F SLAC E87 Fe/D 0.8 SLAC E139 Fe/D 0.8 E665 Ca/D Parameterization Error in parameterization 0.7 0.7 EMC effect 2 3 4 5 6 7 2 3 4 5 6 7 2 3 4 5 6 7 0.001 0.01 0.1 1 x 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 71 ν FromFrom SFsSFs toto PDFsPDFs • As you all know, there is a large industry in determining Parton Distributions to the point where some of my colleagues on collider experiments might think of parton distributions as an annoying piece of FORTRAN code in their C++ software • The purpose, of course, exactly related to Chris’ point about factorization in his Friday lecture 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 72 ν FromFrom SFsSFs toto PDFsPDFs (cont(cont’’d)d) • We just learned that… νν()NCC , 2()()()xF1 x=+ xq x xq x νν()NCC , xFxxuxxdxxsxcx3 ()=+±−Val () Val () 2(() ()) where uVal ( x )=− ux ( ) ux ( ) • In charged-lepton DIS 2 γ p 2 2()xFx1 =+( 3 ) ∑ qxqx ()() up type quarks 2 1 ++()3 ∑ qx() qx () down type quarks • So you begin to see how one can combine neutrino and charged lepton DIS and separate the quark sea from valence quarks up quarks from down quarks 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 73 ν DIS:DIS: MassiveMassive QuarksQuarks andand LeptonsLeptons 12-15 August 2006 Kevin McFarland: Interactions of Neutrinos 74 ν OperaOpera atat CNGSCNGS 1 mm Goal: ντ appearance • 0.15 MWatt source τ ν • high energy νμ beam • 732 km baseline • handfuls of events/yr 1.8kTon Pb Emulsion layers figures courtesy D.
Load more

Recommended publications
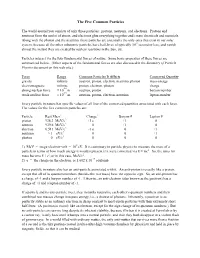
  • The Five Common Particles
    The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2.
    [Show full text]
  • Lepton Flavor and Number Conservation, and Physics Beyond the Standard Model
    Lepton Flavor and Number Conservation, and Physics Beyond the Standard Model Andr´ede Gouv^ea1 and Petr Vogel2 1 Department of Physics and Astronomy, Northwestern University, Evanston, Illinois, 60208, USA 2 Kellogg Radiation Laboratory, Caltech, Pasadena, California, 91125, USA April 1, 2013 Abstract The physics responsible for neutrino masses and lepton mixing remains unknown. More ex- perimental data are needed to constrain and guide possible generalizations of the standard model of particle physics, and reveal the mechanism behind nonzero neutrino masses. Here, the physics associated with searches for the violation of lepton-flavor conservation in charged-lepton processes and the violation of lepton-number conservation in nuclear physics processes is summarized. In the first part, several aspects of charged-lepton flavor violation are discussed, especially its sensitivity to new particles and interactions beyond the standard model of particle physics. The discussion concentrates mostly on rare processes involving muons and electrons. In the second part, the sta- tus of the conservation of total lepton number is discussed. The discussion here concentrates on current and future probes of this apparent law of Nature via searches for neutrinoless double beta decay, which is also the most sensitive probe of the potential Majorana nature of neutrinos. arXiv:1303.4097v2 [hep-ph] 29 Mar 2013 1 1 Introduction In the absence of interactions that lead to nonzero neutrino masses, the Standard Model Lagrangian is invariant under global U(1)e × U(1)µ × U(1)τ rotations of the lepton fields. In other words, if neutrinos are massless, individual lepton-flavor numbers { electron-number, muon-number, and tau-number { are expected to be conserved.
    [Show full text]
  • Neutrino Opacity I. Neutrino-Lepton Scattering*
    PHYSICAL REVIEW VOLUME 136, NUMBER 4B 23 NOVEMBER 1964 Neutrino Opacity I. Neutrino-Lepton Scattering* JOHN N. BAHCALL California Institute of Technology, Pasadena, California (Received 24 June 1964) The contribution of neutrino-lepton scattering to the total neutrino opacity of matter is investigated; it is found that, contrary to previous beliefs, neutrino scattering dominates the neutrino opacity for many astro­ physically important conditions. The rates for neutrino-electron scattering and antineutrino-electron scatter­ ing are given for a variety of conditions, including both degenerate and nondegenerate gases; the rates for some related reactions are also presented. Formulas are given for the mean scattering angle and the mean energy loss in neutrino and antineutrino scattering. Applications are made to the following problems: (a) the detection of solar neutrinos; (b) the escape of neutrinos from stars; (c) neutrino scattering in cosmology; and (d) energy deposition in supernova explosions. I. INTRODUCTION only been discussed for the special situation of electrons 13 14 XPERIMENTS1·2 designed to detect solar neu­ initially at rest. · E trinos will soon provide crucial tests of the theory In this paper, we investigate the contribution of of stellar energy generation. Other neutrino experiments neutrino-lepton scattering to the total neutrino opacity have been suggested as a test3 of a possible mechanism of matter and show, contrary to previous beliefs, that for producing the high-energy electrons that are inferred neutrino-lepton scattering dominates the neutrino to exist in strong radio sources and as a means4 for opacity for many astrophysically important conditions. studying the high-energy neutrinos emitted in the decay Here, neutrino opacity is defined, analogously to photon of cosmic-ray secondaries.
    [Show full text]
  • Opportunities for Neutrino Physics at the Spallation Neutron Source (SNS)
    Opportunities for Neutrino Physics at the Spallation Neutron Source (SNS) Paper submitted for the 2008 Carolina International Symposium on Neutrino Physics Yu Efremenko1,2 and W R Hix2,1 1University of Tennessee, Knoxville TN 37919, USA 2Oak Ridge National Laboratory, Oak Ridge TN 37981, USA E-mail: [email protected] Abstract. In this paper we discuss opportunities for a neutrino program at the Spallation Neutrons Source (SNS) being commissioning at ORNL. Possible investigations can include study of neutrino-nuclear cross sections in the energy rage important for supernova dynamics and neutrino nucleosynthesis, search for neutrino-nucleus coherent scattering, and various tests of the standard model of electro-weak interactions. 1. Introduction It seems that only yesterday we gathered together here at Columbia for the first Carolina Neutrino Symposium on Neutrino Physics. To my great astonishment I realized it was already eight years ago. However by looking back we can see that enormous progress has been achieved in the field of neutrino science since that first meeting. Eight years ago we did not know which region of mixing parameters (SMA. LMA, LOW, Vac) [1] would explain the solar neutrino deficit. We did not know whether this deficit is due to neutrino oscillations or some other even more exotic phenomena, like neutrinos decay [2], or due to the some other effects [3]. Hints of neutrino oscillation of atmospheric neutrinos had not been confirmed in accelerator experiments. Double beta decay collaborations were just starting to think about experiments with sensitive masses of hundreds of kilograms. Eight years ago, very few considered that neutrinos can be used as a tool to study the Earth interior [4] or for non- proliferation [5].
    [Show full text]
  • Neutrino Physics
    SLAC Summer Institute on Particle Physics (SSI04), Aug. 2-13, 2004 Neutrino Physics Boris Kayser Fermilab, Batavia IL 60510, USA Thanks to compelling evidence that neutrinos can change flavor, we now know that they have nonzero masses, and that leptons mix. In these lectures, we explain the physics of neutrino flavor change, both in vacuum and in matter. Then, we describe what the flavor-change data have taught us about neutrinos. Finally, we consider some of the questions raised by the discovery of neutrino mass, explaining why these questions are so interesting, and how they might be answered experimentally, 1. PHYSICS OF NEUTRINO OSCILLATION 1.1. Introduction There has been a breakthrough in neutrino physics. It has been discovered that neutrinos have nonzero masses, and that leptons mix. The evidence for masses and mixing is the observation that neutrinos can change from one type, or “flavor”, to another. In this first section of these lectures, we will explain the physics of neutrino flavor change, or “oscillation”, as it is called. We will treat oscillation both in vacuum and in matter, and see why it implies masses and mixing. That neutrinos have masses means that there is a spectrum of neutrino mass eigenstates νi, i = 1, 2,..., each with + a mass mi. What leptonic mixing means may be understood by considering the leptonic decays W → νi + `α of the W boson. Here, α = e, µ, or τ, and `e is the electron, `µ the muon, and `τ the tau. The particle `α is referred to as the charged lepton of flavor α.
    [Show full text]
  • Heavy Neutrino Search Via Semileptonic Higgs Decay at the LHC
    Eur. Phys. J. C (2019) 79:424 https://doi.org/10.1140/epjc/s10052-019-6937-7 Regular Article - Theoretical Physics Heavy neutrino search via semileptonic higgs decay at the LHC Arindam Das1,2,3,a,YuGao4,5,b, Teruki Kamon6,c 1 School of Physics, KIAS, Seoul 02455, Korea 2 Department of Physics and Astronomy, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Korea 3 Korea Neutrino Research Center, Seoul National University, Bldg 23-312, Sillim-dong, Gwanak-gu, Seoul 08826, Korea 4 Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China 5 Department of Physics and Astronomy, Wayne State University, Detroit 48201, USA 6 Mitchell Institute for Fundamental Physics and Astronomy, Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA Received: 25 September 2018 / Accepted: 11 May 2019 / Published online: 20 May 2019 © The Author(s) 2019 Abstract In the inverse see-saw model the effective neu- the scale of top quark Yukawa coupling (YD ∼ 1) to the scale −6 trino Yukawa couplings can be sizable due to a large mixing of electron Yukawa coupling (YD ∼ 10 ). angle between the light (ν)and heavy neutrinos (N). When In high energy collider experimental point of view, it the right handed neutrino (N) can be lighter than the Stan- is interesting if the heavy neutrino mass lies at the TeV dard Model (SM) Higgs boson (h). It can be produced via scale or smaller, because such heavy neutrinos could be pro- the on-shell decay of the Higgs, h → Nν at a significant duced at high energy colliders, such as the Large Hadron branching fraction at the LHC.
    [Show full text]
  • Strange Mesons (S = ±1, C = B = 0)
    Citation: M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98, 030001 (2018) STRANGE MESONS (S = 1, C = B = 0) K + = us, K 0 = ds, K±0 = d s, K − = u s, similarly for K ∗’s ± P 1 K I (J ) = 2 (0−) Mass m = 493.677 0.016 MeV [a] (S = 2.8) ± Mean life τ = (1.2380 0.0020) 10−8 s (S=1.8) ± × cτ = 3.711 m CPT violation parameters (∆ = rate difference/sum) ∆(K ± µ± ν )=( 0.27 0.21)% → µ − ± ∆(K ± π± π0) = (0.4 0.6)% [b] → ± CP violation parameters (∆ = rate difference/sum) ∆(K ± π± e+ e−)=( 2.2 1.6) 10−2 → − ± × ∆(K ± π± µ+ µ−)=0.010 0.023 → ± ∆(K ± π± π0 γ) = (0.0 1.2) 10−3 → ± × ∆(K ± π± π+ π−) = (0.04 0.06)% → ± ∆(K ± π± π0 π0)=( 0.02 0.28)% → − ± T violation parameters K + π0 µ+ ν P = ( 1.7 2.5) 10−3 → µ T − ± × K + µ+ ν γ P = ( 0.6 1.9) 10−2 → µ T − ± × K + π0 µ+ ν Im(ξ) = 0.006 0.008 → µ − ± Slope parameter g [c] (See Particle Listings for quadratic coefficients and alternative parametrization re- lated to ππ scattering) K ± π± π+ π− g = 0.21134 0.00017 → − ± (g g )/(g + g )=( 1.5 2.2) 10−4 + − − + − − ± × K ± π± π0 π0 g = 0.626 0.007 → ± (g g )/(g + g ) = (1.8 1.8) 10−4 + − − + − ± × K ± decay form factors [d,e] Assuming µ-e universality λ (K + ) = λ (K + ) = (2.97 0.05) 10−2 + µ3 + e3 ± × λ (K + ) = (1.95 0.12) 10−2 0 µ3 ± × HTTP://PDG.LBL.GOV Page1 Created:6/5/201818:58 Citation: M.
    [Show full text]
  • Phenomenology of Sterile Neutrinos
    Phenomenology of sterile neutrinos Carlo Giunti INFN, Sezione di Torino, Via P. Giuria 1, I–10125 Torino, Italy E-mail: [email protected] Abstract. The indications in favor of short-baseline neutrino oscillations, which require the existence of one or more sterile neutrinos, are reviewed. In the framework of 3+1 neutrino mixing, which is the simplest extension of the standard three-neutrino mixing which can partially explain the data, there is a strong tension in the interpretation of the data, mainly due to an incompatibility of the results of appearance and disappearance experiments. In the framework of 3+2 neutrino mixing, CP violation in short-baseline experiments can explain the difference between MiniBooNE neutrino and antineutrino data, but the tension between the data of appearance and disappearance experiments persists because the short-baseline disappearance of electron antineutrinos and muon neutrinos compatible with the LSND and MiniBooNE antineutrino appearance signal has not been observed. 1. Introduction From the results of solar, atmospheric and long-baseline neutrino oscillation experiments we know that neutrinos are massive and mixed particles (see [1]). There are two groups of experiments which measured two independent squared-mass differences (∆m2) in two different neutrino flavor transition channels: • Solar neutrino experiments (Homestake, Kamiokande, GALLEX/GNO, SAGE, Super- 2 Kamiokande, SNO, BOREXino) measured νe → νµ,ντ oscillations generated by ∆mSOL = +1.1 −5 2 2 +0.04 6.2−1.9 ×10 eV and a mixing angle tan ϑSOL = 0.42−0.02 [2]. The KamLAND experiment confirmed these oscillations by observing the disappearance of reactorν ¯e at an average distance of about 180 km.
    [Show full text]
  • Phenomenology of Gev-Scale Heavy Neutral Leptons Arxiv:1805.08567
    Prepared for submission to JHEP INR-TH-2018-014 Phenomenology of GeV-scale Heavy Neutral Leptons Kyrylo Bondarenko,1 Alexey Boyarsky,1 Dmitry Gorbunov,2;3 Oleg Ruchayskiy4 1Intituut-Lorentz, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands 2Institute for Nuclear Research of the Russian Academy of Sciences, Moscow 117312, Russia 3Moscow Institute of Physics and Technology, Dolgoprudny 141700, Russia 4Discovery Center, Niels Bohr Institute, Copenhagen University, Blegdamsvej 17, DK- 2100 Copenhagen, Denmark E-mail: [email protected], [email protected], [email protected], [email protected] Abstract: We review and revise phenomenology of the GeV-scale heavy neutral leptons (HNLs). We extend the previous analyses by including more channels of HNLs production and decay and provide with more refined treatment, including QCD corrections for the HNLs of masses (1) GeV. We summarize the relevance O of individual production and decay channels for different masses, resolving a few discrepancies in the literature. Our final results are directly suitable for sensitivity studies of particle physics experiments (ranging from proton beam-dump to the LHC) aiming at searches for heavy neutral leptons. arXiv:1805.08567v3 [hep-ph] 9 Nov 2018 ArXiv ePrint: 1805.08567 Contents 1 Introduction: heavy neutral leptons1 1.1 General introduction to heavy neutral leptons2 2 HNL production in proton fixed target experiments3 2.1 Production from hadrons3 2.1.1 Production from light unflavored and strange mesons5 2.1.2
    [Show full text]
  • Detection of a Strange Particle
    10 extraordinary papers Within days, Watson and Crick had built a identify the full set of codons was completed in forensics, and research into more-futuristic new model of DNA from metal parts. Wilkins by 1966, with Har Gobind Khorana contributing applications, such as DNA-based computing, immediately accepted that it was correct. It the sequences of bases in several codons from is well advanced. was agreed between the two groups that they his experiments with synthetic polynucleotides Paradoxically, Watson and Crick’s iconic would publish three papers simultaneously in (see go.nature.com/2hebk3k). structure has also made it possible to recog- Nature, with the King’s researchers comment- With Fred Sanger and colleagues’ publica- nize the shortcomings of the central dogma, ing on the fit of Watson and Crick’s structure tion16 of an efficient method for sequencing with the discovery of small RNAs that can reg- to the experimental data, and Franklin and DNA in 1977, the way was open for the com- ulate gene expression, and of environmental Gosling publishing Photograph 51 for the plete reading of the genetic information in factors that induce heritable epigenetic first time7,8. any species. The task was completed for the change. No doubt, the concept of the double The Cambridge pair acknowledged in their human genome by 2003, another milestone helix will continue to underpin discoveries in paper that they knew of “the general nature in the history of DNA. biology for decades to come. of the unpublished experimental results and Watson devoted most of the rest of his ideas” of the King’s workers, but it wasn’t until career to education and scientific administra- Georgina Ferry is a science writer based in The Double Helix, Watson’s explosive account tion as head of the Cold Spring Harbor Labo- Oxford, UK.
    [Show full text]
  • Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons And/Or Other HTM Scalars at Hadron Colliders
    S S symmetry Article Production of the Doubly Charged Higgs Boson in Association with the SM Gauge Bosons and/or Other HTM Scalars at Hadron Colliders Bartosz Dziewit 1,* , Magdalena Kordiaczy ´nska 1 and Tripurari Srivastava 2 1 Institute of Physics, University of Silesia, 40-007 Katowice, Poland; [email protected] 2 Department of Physics, DIT University Dehradun, Uttarakhand 248009, India; [email protected] * Correspondence: [email protected] Abstract: We investigate an extension of the Standard Model with one additional triplet of scalar bosons. Altogether, the model contains four Higgs bosons. We analyze the associated production of the doubly charged scalar with the Standard Model gauge bosons and the remaining Higgs bosons of the model, which are: the light (SM) and heavy neutral scalars and a singly charged scalar. We estimate, in the context of the present (HL–LHC) and future (FCC–hh) hadron colliders, the most promising processes in which a single produced doubly charged Higgs boson is involved. Keywords: theoretical physics; particle physics; Standard Model; Higgs triplets; doubly charged Higgs bosons; hadron colliders Citation: Dziewit, B.; Kordiaczy´nska, M.; Srivastava, T. Production of the Doubly Charged Higgs Boson in 1. Introduction Association with the SM Gauge Bosons and/or Other HTM Scalars at Experimental evidence of the Higgs boson’s existence, found at the Large Hadron Hadron Colliders. Symmetry 2021, 13, Collider (LHC) [1,2], was a quantum leap in particle physics history. Nevertheless, ques- 1240. https://doi.org/10.3390/ tions related to the minimal Higgs sector are still open. From this point of view, extensions sym13071240 of the Standard Model can be realized in two ways: directly, by introducing additional multiplets, or indirectly, by extending the gauge group (e.g., left right symmetric mod- Academic Editors: Zoltán Trócsányi, els [3–8]).
    [Show full text]
  • Tritium Beta Decay and the Search for Neutrino Mass
    ritium Beta Decay and the Search for Neutrino Mass Tritium Beta Decay and the Search for Neutrino Mass eutrinos have been around, that the decay also produced a second neutrino mass. A short lifetime literally, since the beginning unseen particle, now called the means atoms decay more rapidly, Nof time. In the sweltering electron neutrino. The neutrino would making more data available. moments following the Big Bang, share the energy released in the decay A wonderful accident of nature, tri- neutrinos were among the first particles with the daughter atom and the tium (a hydrogen atom with two extra Tritium Beta Decay and the Search to emerge from the primordial sea. electron. The electrons would emerge neutrons) is a perfect source by both A minute later, the universe had cooled with a spectrum of energies. of these measures: it has a reasonably for Neutrino Mass enough for protons and neutrons In 1934, Enrico Fermi pointed out short lifetime (12.4 years) and releases to bind together and form atomic that, if the neutrino had mass, it would only 18.6 kilo-electron-volts (keV) Thomas J. Bowles and R. G. Hamish Robertson as told to David Kestenbaum nuclei. Ten or twenty billion years subtly distort the tail of this spectrum. as it decays into helium-3. later—today—the universe still teems When an atom undergoes beta decay, it Additionally, its molecular structure with these ancient neutrinos, which produces a specific amount of available is simple enough that the energy outnumber protons and neutrons by energy that is carried away by the spectrum of the decay electrons can roughly a billion to one.
    [Show full text]