Investment Performance and Price-Earnings Ratios: Basu 1977 Revisited
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Fact Sheet 2021
Q2 2021 GCI Select Equity TM Globescan Capital was Returns (Average Annual) Morningstar Rating (as of 3/31/21) © 2021 Morningstar founded on the principle Return Return that investing in GCI Select S&P +/- Percentile Quartile Overall Funds in high-quality companies at Equity 500TR Rank Rank Rating Category attractive prices is the best strategy to achieve long-run Year to Date 18.12 15.25 2.87 Q1 2021 Top 30% 2nd 582 risk-adjusted performance. 1-year 43.88 40.79 3.08 1 year Top 19% 1st 582 As such, our portfolio is 3-year 22.94 18.67 4.27 3 year Top 3% 1st 582 concentrated and focused solely on the long-term, Since Inception 20.94 17.82 3.12 moat-protected future free (01/01/17) cash flows of the companies we invest in. TOP 10 HOLDINGS PORTFOLIO CHARACTERISTICS Morningstar Performance MPT (6/30/2021) (6/30/2021) © 2021 Morningstar Core Principles Facebook Inc A 6.76% Number of Holdings 22 Return 3 yr 19.49 Microsoft Corp 6.10% Total Net Assets $44.22M Standard Deviation 3 yr 18.57 American Tower Corp 5.68% Total Firm Assets $119.32M Alpha 3 yr 3.63 EV/EBITDA (ex fincls/reits) 17.06x Upside Capture 3yr 105.46 Crown Castle International Corp 5.56% P/E FY1 (ex fincls/reits) 29.0x Downside Capture 3 yr 91.53 Charles Schwab Corp 5.53% Invest in businesses, EPS Growth (ex fincls/reits) 25.4% Sharpe Ratio 3 yr 1.04 don't trade stocks United Parcel Service Inc Class B 5.44% ROIC (ex fincls/reits) 14.1% Air Products & Chemicals Inc 5.34% Standard Deviation (3-year) 18.9% Booking Holding Inc 5.04% % of assets in top 5 holdings 29.6% Mastercard Inc A 4.74% % of assets in top 10 holdings 54.7% First American Financial Corp 4.50% Dividend Yield 0.70% Think long term, don't try to time markets Performance vs S&P 500 (Average Annual Returns) Be concentrated, 43.88 GCI Select Equity don't overdiversify 40.79 S&P 500 TR 22.94 20.94 18.12 18.67 17.82 15.25 Use the market, don't rely on it YTD 1 YR 3 YR Inception (01/01/2017) Disclosures Globescan Capital Inc., d/b/a GCI-Investors, is an investment advisor registered with the SEC. -

2G-Amp-3G-Mobile-Communication
2G & 3G Mobile Communication Contents 1 Executive Summary ................................................................................................................. 3 2 Introduction ............................................................................................................................. 4 2.1 Overview of 2G & 3G Technology ............................................................................................................... 4 2.2 Technical Highlights of 2G & 3G .................................................................................................................. 4 2.3 Comparative Study of 2G, 3G & 4G-LTE ...................................................................................................... 5 3 Analysis of the 2G & 3G Patent Landscape ............................................................................. 7 3.1 Patent Categories & Distribution ................................................................................................................ 7 3.2 Top Patent Holders ...................................................................................................................................... 7 3.3 Analysis of Seminal Patents ......................................................................................................................... 9 3.4 Analysis of Standard-Essential Patents ..................................................................................................... 12 3.5 Patent Filing and Grant Trends ................................................................................................................. -

Catholic United Investment Trust Annual Report
CATHOLIC UNITED INVESTMENT TRUST ANNUAL REPORT (AUDITED) December 31, 2015 CATHOLIC UNITED INVESTMENT TRUST TABLE OF CONTENTS Page REPORT OF INDEPENDENT AUDITORS 1-2 Statement of Assets and Liabilities 3-4 Schedule of Investments: Money Market Fund 5-7 Short Bond Fund 8-11 Intermediate Diversified Bond Fund 12-21 Opportunistic Bond Fund 22-27 Balanced Fund 28-38 Value Equity Fund 39-41 Core Equity Index Fund 42-48 Growth Fund 49-52 International Equity Fund 53-56 Small Capitalization Equity Index Fund 57-73 Statements of Operations 74-76 Statements of Changes in Net Assets 77-79 NOTES TO FINANCIAL STATEMENTS 80-92 FINANCIAL HIGHLIGHTS 93-95 Crowe Horwath LLP Independent Member Crowe Horwath International INDEPENDENT AUDITOR'S REPORT To the Members of the Board of Trustees and Unit-holders of Catholic United Investment Trust Report on the Financial Statements We have audited the accompanying financial statements of Catholic United Investment Trust – Money Market Fund, Short Bond Fund, Intermediate Diversified Bond Fund, Opportunistic Bond Fund, Balanced Fund, Value Equity Fund, Core Equity Index Fund, Growth Fund, International Equity Fund, and Small Capitalization Equity Index Fund (the “Trust”), which comprise the statement of assets and liabilities as of December 31, 2015, the schedule of investments as of December 31, 2015, the related statements of operations and statements of changes in net assets for the periods ended December 31, 2015 and 2014, and the financial highlights for the periods ended December 31, 2015 and 2014, and the related notes to the financial statements. Management’s Responsibility for the Financial Statements Management is responsible for the preparation and fair presentation of these financial statements in accordance with accounting principles generally accepted in the United States of America; this includes the design, implementation, and maintenance of internal control relevant to the preparation and fair presentation of financial statements that are free from material misstatement, whether due to fraud or error. -

Introductory Note
Introductory Note: Section 58 of the New Zealand Superannuation and Retirement Income Act 2001 requires that the Guardians must invest the Fund on a prudent, commercial basis, and in a manner consistent with best-practice portfolio management. The Guardians have determined that this requires broad diversification of investments. The Fund’s investment strategy includes holding investments benchmarked to global market indices. On 30 June 2011, the Fund’s portfolio held over 6000 listed companies, providing diversification across most of the world’s countries and industries. The Table below sets out our direct exposure to listed companies, by country of exposure. Country of exposure is defined as location of the ultimate global parent's place of incorporation, except in the case of tax haven countries, where we instead look to the place of business for the headquarters of the ultimate global parent. The Fund also has indirect exposure to other companies through total return swaps linked to market indices and through investment in pooled funds. As the Fund increases in value, both the number of securities and the average size of each holding tend to increase. Security Name Value in New Zealand Dollars Australia Abacus Property Group 32,897 Acrux Ltd 36,391 Adelaide Brighton Ltd 101,165 AGL Energy Ltd 1,957,445 Alesco Corp Ltd 19,809 Alkane Resources Ltd 28,026 Alumina Ltd 145,456 Amcor Ltd 255,625 AMP Ltd 4,032,208 Ansell Ltd 116,456 APA Group 131,716 APN News & Media Ltd 2,829,583 Aquila Resources Ltd 84,275 ARB Corp Ltd 32,632 Ardent Leisure -

H-1B Petition Approvals for Initial Benefits by Employers FY07
NUMBER OF H-1B PETITIONS APPROVED BY USCIS FOR INITIAL BENEFICIARIES FY 2007 Approved Employer Petitions INFOSYS TECHNOLOGIES LIMITED 4,559 WIPRO LIMITED 2,567 SATYAM COMPUTER SERVICES LTD 1,396 COGNIZANT TECH SOLUTIONS US CORP 962 MICROSOFT CORP 959 TATA CONSULTANCY SERVICES LIMITED 797 PATNI COMPUTER SYSTEMS INC 477 US TECHNOLOGY RESOURCES LLC 416 I-FLEX SOLUTIONS INC 374 INTEL CORPORATION 369 ACCENTURE LLP 331 CISCO SYSTEMS INC 324 ERNST & YOUNG LLP 302 LARSEN & TOUBRO INFOTECH LIMITED 292 DELOITTE & TOUCHE LLP 283 GOOGLE INC 248 MPHASIS CORPORATION 248 UNIVERSITY OF ILLINOIS AT CHICAGO 246 AMERICAN UNIT INC 245 JSMN INTERNATIONAL INC 245 OBJECTWIN TECHNOLOGY INC 243 DELOITTE CONSULTING LLP 242 PRINCE GEORGES COUNTY PUBLIC SCHS 238 JPMORGAN CHASE & CO 236 MOTOROLA INC 234 MARLABS INC 229 KPMG LLP 227 GOLDMAN SACHS & CO 224 TECH MAHINDRA AMERICAS INC 217 VERINON TECHNOLOGY SOLUTIONS LTD 213 THE JOHNS HOPKINS MED INSTS OIS 205 YASH TECHNOLOGIES INC 202 ADVANSOFT INTERNATIONAL INC 201 UNIVERSITY OF MARYLAND 199 BALTIMORE CITY PUBLIC SCHOOLS 196 PRICEWATERHOUSECOOPERS LLP 192 POLARIS SOFTWARE LAB INDIA LTD 191 UNIVERSITY OF MICHIGAN 191 EVEREST BUSINESS SOLUTIONS INC 190 IBM CORPORATION 184 APEX TECHNOLOGY GROUP INC 174 NEW YORK CITY PUBLIC SCHOOLS 171 SOFTWARE RESEARCH GROUP INC 167 EVEREST CONSULTING GROUP INC 165 UNIVERSITY OF PENNSYLVANIA 163 GSS AMERICA INC 160 QUALCOMM INCORPORATED 158 UNIVERSITY OF MINNESOTA 151 MASCON GLOBAL CONSULTING INC 150 MICRON TECHNOLOGY INC 149 THE OHIO STATE UNIVERSITY 147 STANFORD UNIVERSITY 146 COLUMBIA -

Lapis Global Top 50 Dividend Yield Index Ratios
Lapis Global Top 50 Dividend Yield Index Ratios MARKET RATIOS 2012 2013 2014 2015 2016 2017 2018 2019 2020 P/E Lapis Global Top 50 DY Index 14,45 16,07 16,71 17,83 21,06 22,51 14,81 16,96 19,08 MSCI ACWI Index (Benchmark) 15,42 16,78 17,22 19,45 20,91 20,48 14,98 19,75 31,97 P/E Estimated Lapis Global Top 50 DY Index 12,75 15,01 16,34 16,29 16,50 17,48 13,18 14,88 14,72 MSCI ACWI Index (Benchmark) 12,19 14,20 14,94 15,16 15,62 16,23 13,01 16,33 19,85 P/B Lapis Global Top 50 DY Index 2,52 2,85 2,76 2,52 2,59 2,92 2,28 2,74 2,43 MSCI ACWI Index (Benchmark) 1,74 2,02 2,08 2,05 2,06 2,35 2,02 2,43 2,80 P/S Lapis Global Top 50 DY Index 1,49 1,70 1,72 1,65 1,71 1,93 1,44 1,65 1,60 MSCI ACWI Index (Benchmark) 1,08 1,31 1,35 1,43 1,49 1,71 1,41 1,72 2,14 EV/EBITDA Lapis Global Top 50 DY Index 9,52 10,45 10,77 11,19 13,07 13,01 9,92 11,82 12,83 MSCI ACWI Index (Benchmark) 8,93 9,80 10,10 11,18 11,84 11,80 9,99 12,22 16,24 FINANCIAL RATIOS 2012 2013 2014 2015 2016 2017 2018 2019 2020 Debt/Equity Lapis Global Top 50 DY Index 89,71 93,46 91,08 95,51 96,68 100,66 97,56 112,24 127,34 MSCI ACWI Index (Benchmark) 155,55 137,23 133,62 131,08 134,68 130,33 125,65 129,79 140,13 PERFORMANCE MEASURES 2012 2013 2014 2015 2016 2017 2018 2019 2020 Sharpe Ratio Lapis Global Top 50 DY Index 1,48 2,26 1,05 -0,11 0,84 3,49 -1,19 2,35 -0,15 MSCI ACWI Index (Benchmark) 1,23 2,22 0,53 -0,15 0,62 3,78 -0,93 2,27 0,56 Jensen Alpha Lapis Global Top 50 DY Index 3,2 % 2,2 % 4,3 % 0,3 % 2,9 % 2,3 % -3,9 % 2,4 % -18,6 % Information Ratio Lapis Global Top 50 DY Index -0,24 -

Arbitrage Pricing Theory: Theory and Applications to Financial Data Analysis Basic Investment Equation
Risk and Portfolio Management Spring 2010 Arbitrage Pricing Theory: Theory and Applications To Financial Data Analysis Basic investment equation = Et equity in a trading account at time t (liquidation value) = + Δ Rit return on stock i from time t to time t t (includes dividend income) = Qit dollars invested in stock i at time t r = interest rate N N = + Δ + − ⎛ ⎞ Δ ()+ Δ Et+Δt Et Et r t ∑Qit Rit ⎜∑Qit ⎟r t before rebalancing, at time t t i=1 ⎝ i=1 ⎠ N N N = + Δ + − ⎛ ⎞ Δ + ε ()+ Δ Et+Δt Et Et r t ∑Qit Rit ⎜∑Qit ⎟r t ∑| Qi(t+Δt) - Qit | after rebalancing, at time t t i=1 ⎝ i=1 ⎠ i=1 ε = transaction cost (as percentage of stock price) Leverage N N = + Δ + − ⎛ ⎞ Δ Et+Δt Et Et r t ∑Qit Rit ⎜∑Qit ⎟r t i=1 ⎝ i=1 ⎠ N ∑ Qit Ratio of (gross) investments i=1 Leverage = to equity Et ≥ Qit 0 ``Long - only position'' N ≥ = = Qit 0, ∑Qit Et Leverage 1, long only position i=1 Reg - T : Leverage ≤ 2 ()margin accounts for retail investors Day traders : Leverage ≤ 4 Professionals & institutions : Risk - based leverage Portfolio Theory Introduce dimensionless quantities and view returns as random variables Q N θ = i Leverage = θ Dimensionless ``portfolio i ∑ i weights’’ Ei i=1 ΔΠ E − E − E rΔt ΔE = t+Δt t t = − rΔt Π Et E ~ All investments financed = − Δ Ri Ri r t (at known IR) ΔΠ N ~ = θ Ri Π ∑ i i=1 ΔΠ N ~ ΔΠ N ~ ~ N ⎛ ⎞ ⎛ ⎞ 2 ⎛ ⎞ ⎛ ⎞ E = θ E Ri ; σ = θ θ Cov Ri , R j = θ θ σ σ ρ ⎜ Π ⎟ ∑ i ⎜ ⎟ ⎜ Π ⎟ ∑ i j ⎜ ⎟ ∑ i j i j ij ⎝ ⎠ i=1 ⎝ ⎠ ⎝ ⎠ ij=1 ⎝ ⎠ ij=1 Sharpe Ratio ⎛ ΔΠ ⎞ N ⎛ ~ ⎞ E θ E R ⎜ Π ⎟ ∑ i ⎜ i ⎟ s = s()θ ,...,θ = ⎝ ⎠ = i=1 ⎝ ⎠ 1 N ⎛ ΔΠ ⎞ N σ ⎜ ⎟ θ θ σ σ ρ Π ∑ i j i j ij ⎝ ⎠ i=1 Sharpe ratio is homogeneous of degree zero in the portfolio weights. -
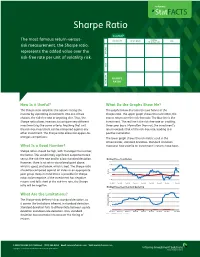
Sharpe Ratio
StatFACTS Sharpe Ratio StatMAP CAPITAL The most famous return-versus- voLATILITY BENCHMARK TAIL PRESERVATION risk measurement, the Sharpe ratio, RN TU E represents the added value over the R risk-free rate per unit of volatility risk. K S I R FF O - E SHARPE AD R RATIO T How Is it Useful? What Do the Graphs Show Me? The Sharpe ratio simplifies the options facing the The graphs below illustrate the two halves of the investor by separating investments into one of two Sharpe ratio. The upper graph shows the numerator, the choices, the risk-free rate or anything else. Thus, the excess return over the risk-free rate. The blue line is the Sharpe ratio allows investors to compare very different investment. The red line is the risk-free rate on a rolling, investments by the same criteria. Anything that isn’t three-year basis. More often than not, the investment’s the risk-free investment can be compared against any return exceeds that of the risk-free rate, leading to a other investment. The Sharpe ratio allows for apples-to- positive numerator. oranges comparisons. The lower graph shows the risk metric used in the denominator, standard deviation. Standard deviation What Is a Good Number? measures how volatile an investment’s returns have been. Sharpe ratios should be high, with the larger the number, the better. This would imply significant outperformance versus the risk-free rate and/or a low standard deviation. Rolling Three Year Return However, there is no set-in-stone breakpoint above, 40% 30% which is good, and below, which is bad. -

A Sharper Ratio: a General Measure for Correctly Ranking Non-Normal Investment Risks
A Sharper Ratio: A General Measure for Correctly Ranking Non-Normal Investment Risks † Kent Smetters ∗ Xingtan Zhang This Version: February 3, 2014 Abstract While the Sharpe ratio is still the dominant measure for ranking risky investments, much effort has been made over the past three decades to find more robust measures that accommodate non- Normal risks (e.g., “fat tails”). But these measures have failed to map to the actual investor problem except under strong restrictions; numerous ad-hoc measures have arisen to fill the void. We derive a generalized ranking measure that correctly ranks risks relative to the original investor problem for a broad utility-and-probability space. Like the Sharpe ratio, the generalized measure maintains wealth separation for the broad HARA utility class. The generalized measure can also correctly rank risks following different probability distributions, making it a foundation for multi-asset class optimization. This paper also explores the theoretical foundations of risk ranking, including proving a key impossibility theorem: any ranking measure that is valid for non-Normal distributions cannot generically be free from investor preferences. Finally, we show that approximation measures, which have sometimes been used in the past, fail to closely approximate the generalized ratio, even if those approximations are extended to an infinite number of higher moments. Keywords: Sharpe Ratio, portfolio ranking, infinitely divisible distributions, generalized rank- ing measure, Maclaurin expansions JEL Code: G11 ∗Kent Smetters: Professor, The Wharton School at The University of Pennsylvania, Faculty Research Associate at the NBER, and affiliated faculty member of the Penn Graduate Group in Applied Mathematics and Computational Science. -

In-Sample and Out-Of-Sample Sharpe Ratios of Multi-Factor Asset Pricing Models
In-sample and Out-of-sample Sharpe Ratios of Multi-factor Asset Pricing Models RAYMOND KAN, XIAOLU WANG, and XINGHUA ZHENG∗ This version: November 2020 ∗Kan is from the University of Toronto, Wang is from Iowa State University, and Zheng is from Hong Kong University of Science and Technology. We thank Svetlana Bryzgalova, Peter Christoffersen, Victor DeMiguel, Andrew Detzel, Junbo Wang, Guofu Zhou, seminar participants at Chinese University of Hong Kong, London Business School, Louisiana State University, Uni- versity of Toronto, and conference participants at 2019 CFIRM Conference for helpful comments. Corresponding author: Raymond Kan, Joseph L. Rotman School of Management, University of Toronto, 105 St. George Street, Toronto, Ontario, Canada M5S 3E6; Tel: (416) 978-4291; Fax: (416) 978-5433; Email: [email protected]. In-sample and Out-of-sample Sharpe Ratios of Multi-factor Asset Pricing Models Abstract For many multi-factor asset pricing models proposed in the recent literature, their implied tangency portfolios have substantially higher sample Sharpe ratios than that of the value- weighted market portfolio. In contrast, such high sample Sharpe ratio is rarely delivered by professional fund managers. This makes it difficult for us to justify using these asset pricing models for performance evaluation. In this paper, we explore if estimation risk can explain why the high sample Sharpe ratios of asset pricing models are difficult to realize in reality. In particular, we provide finite sample and asymptotic analyses of the joint distribution of in-sample and out-of-sample Sharpe ratios of a multi-factor asset pricing model. For an investor who does not know the mean and covariance matrix of the factors in a model, the out-of-sample Sharpe ratio of an asset pricing model is substantially worse than its in-sample Sharpe ratio. -

National Pension Reserve Fund Annual Report 2010
-9% 23% Annual Report and Financial Statements 2010 Treasury Building, Grand Canal Street, Dublin 2, Ireland. Telephone: (353 1) 664 0800 Fax: (353 1) 664 0890 30 June 2011 Mr. Michael Noonan, T.D., Minister for Finance, Government Buildings, Upper Merrion Street, Dublin 2 Dear Minister, I have the honour to submit to you the Report and Accounts of the National Pensions Reserve Fund Commission for the year ended 31 December 2010. Yours sincerely, Paul Carty, Chairman National Pensions Reserve Fund Commission Annual Report and Financial Statements 2010 Annual Report and Financial Statements Financial and Report Annual Annual Report and Financial Statements 2 National Pensions Reserve Fund Commission Annual Report and Financial Statements 2010 Contents REPORT From the Chairman 4 Annual Report and Financial Statements Key Facts and Figures 6 Fund Overview 7 Directed Investments 9 Investment Strategy Review 11 Market Review 15 Performance 17 Portfolio Review 19 Responsible Investment 26 Risk, Oversight and Controls 29 Fees and Expenses 30 Current Commissioners 31 Fund Governance 32 FINANCIAL STATEMENTS Commission Members and Other Information 38 Investment Report 39 Statement of Commission’s Responsibilities 40 Statement on the System of Internal Financial Control 41 Report of the Comptroller and Auditor General 43 Accounting Policies 44 Fund Account 46 Net Assets Statement 47 Administration Account 48 Notes to the Accounts 49 Annual Report and Financial Statements PORTFOLIO OF INVESTMENTS Portfolio of Investments 70 Glossary 112 National Treasury Management Agency – Corporate Information 113 3 National Pensions Reserve Fund Commission Annual Report and Financial Statements 2010 From the Chairman The structure of the National Principal developments Pensions Reserve Fund The principal developments during 2010 were: (“NPRF” or “the Fund”) and Annual Report and Financial Statements Financial and Report Annual the outlook for its future have In respect of the Discretionary Portfolio: significantly changed over the – the Commission agreed an updated investment past year. -

United States District Court for the Southern District of New York
UNITED STATES DISTRICT COURT FOR THE SOUTHERN DISTRICT OF NEW YORK PLAINTIFF, Individually and on Behalf of All Others Similarly Situated, CLASS ACTION COMPLAINT FOR Plaintiff, VIOLATION OF THE FEDERAL SECURITIES LAWS v. JURY TRIAL DEMANDED GENERAL ELECTRIC COMPANY, JEFFREY R. IMMELT, JEFFREY S. BORNSTEIN, JOHN L. FLANNERY, and JAMIE MILLER, Defendants. Plaintiff, individually and on behalf of all others similarly situated, alleges the following based on personal knowledge as to Plaintiff and Plaintiff’s own acts, and upon information and belief as to all other matters based upon the investigation conducted by and through Plaintiff’s attorneys, which included, among other things, a review of Securities and Exchange Commission (“SEC”) filings by General Electric Company (“General Electric” or the “Company”), as well as conference call transcripts and media and analyst reports about the Company. Plaintiff believes that substantial evidentiary support will exist for the allegations set forth herein after a reasonable opportunity for discovery. INTRODUCTION 1. This is a class action brought on behalf of all persons or entities who purchased or otherwise acquired the publicly traded securities of General Electric between December 15, 2016 and November 10, 2017, inclusive (the “Class Period”). The action is brought against General Electric and certain of the Company’s current and former senior executives (collectively, “Defendants”) for violations of Sections 10(b) and 20(a) of the Securities Exchange Act of 1934 (the “Exchange Act”), and Rule