DOCSLIB.ORG

Application of a Mass Balance Partitioning Model of Ra-226, Pb-210 and Po-210 to Freshwater Lakes and Streams

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Application of a Mass Balance Partitioning Model of Ra-226, Pb-210 and Po-210 to Freshwater Lakes and Streams Application of a mass balance partitioning model of Ra-226, Pb-210 and Po-210 to freshwater lakes and streams Submitted by: Kevin John Britton Thesis submitted to the Faculty of Graduate and Postdoctoral Studies in partial fulfillment of the requirements for the Master of Science degree specialization in Chemical and Environmental Toxicology (Earth Sciences) Department of Earth Sciences Faculty of Science University of Ottawa Supervisors: Robert Jack Cornett† (Department of Earth Sciences) Ian D Clark (Department of Earth Sciences) Co-Supervisors: Trevor J Stocki (Department of Earth Sciences) Adrienne LM Ethier (Department of Earth Sciences) Thesis Committee: Clément Bataille Laurel Sinclair 2018 November 15 © Kevin John Britton, Ottawa, Canada, 2018 Abstract The objectives of this thesis were: (1) to develop a mass balance partitioning model of the natural uranium-238 series comprising radium-226, lead-210 and polonium-210 and (2) to apply the model to estimate the source and fate of these radionuclides in freshwater lakes and streams. Samples were collected from Ottawa River watershed tributaries and measured for lead-210 and polonium-210 content to determine the water concentrations that were input to the model. The radium-226 partitioning model was developed by reconstructing and analyzing Quantitative Water, Air, Sediment Interaction (QWASI) models of lead for Lake Ontario and Hamilton Harbour and selecting parameters for an updated QWASI model of lead for a Lake Ontario basin. This study gave insight about model basis definition, and partition coefficient and sediment particle constraint. The radium-226 series model was formulated by connecting separate QWASI modules for radium-226, lead-210 and polonium-210 with decay and ingrowth terms. The radium-226 model was applied to studies of Crystal Lake, Wisconsin; Bickford Pond, Massachusetts; and Clinton River, Michigan, using parameters reported in these and other studies. Model error was evident in the applications to Crystal Lake due to underlying lake heterogeneity, to Bickford Pond due to unidentified sources of lead-210 from sediment diffusion or watershed runoff, and to Clinton River from watershed runoff. The model was applied to seven Laurentian Shield lakes in the Ottawa River watershed using the sample measurements as the basis for water concentration inputs. The application showed that hydrologic flushing rate may be a factor in the proportion of watershed atmospheric deposition and overall Pb-210 input to the water. Laurentian Shield Lakes with the lowest hydrologic flushing rates (<3 a-1) had proportions of Pb-210 losses to sediment greater than 85%. In another application to Judge Sissons Lake, Nunavut, the model indicated that the watershed was the source of about 85% of Pb-210 and 98% of Po-210 input to the water, and that a significant geologic component of Pb-210 input to the lake was likely. The model indicated that most of the Pb-210 in Judge Sissons Lake was lost to outflow, and that most of the Po-210 was lost to sediment. The model showed that sedimentation is a better proxy measurement for atmospheric deposition of Pb-210 to the Laurentian lakes than originally estimated. The model also showed that watershed contributions to Judge Sissons Lake could explain the observed background concentrations of Pb-210 and Po-210. ii Acknowledgements I would like to acknowledge and thank Adrienne Ethier and Canadian Nuclear Laboratories (CNL) for initiating this research into adaptation of the HERMES model to uranium series radionuclides. Adrienne provided the original HERMES model, hosted me in the Environmental Protection Branch at CNL, and assisted with manuscript review. I would also like to thank Marilyne Stuart for assuming the role as CNL liaison. I would like to thank Diane Martens at AREVA (Orano) Resources Canada for providing the Kiggavik study data reports. I am most grateful to Jack Cornett at the University of Ottawa who enabled this thesis. I was fortunate for the time he shared with me. He is missed by many students. I would like to thank the staff and students of A. E. Lalonde Laboratory, particularly Barbara Francisco, Soroush Fard and Cole MacDonald. I would like to acknowledge and thank Trevor Stocki at Health Canada. Trevor assumed the role of supervisor after Jack. He gave many detailed reviews during manuscript writing. I would like to express special thanks to Ian Clark for bridging the gap at the University of Ottawa as official supervisor in these final months. Both made completion of this project possible. I would like to acknowledge and thank Jack Cornett and Canadian Nuclear Laboratories for funding this project. iii Statement of Originality Chapter 2 I studied the QWASI aquivalence model for lead in Lake Ontario and Hamilton Harbour developed by Dr. Donald Mackay et al to identify challenges to the planned extension to the Ra-226 series nuclides. I expected that the QWASI aquivalence model applications would be internally and mutually consistent. I studied the model partly by verifying and adapting the HERMES mercury model developed by Dr. Adrienne Ethier et al. to the QWASI lead formulation. I reproduced QWASI aquivalence model applications and confirmed the sources for the parameters cited. I found no unexpected inconsistencies among the QWASI aquivalence model applications, but two of the three did not constrain particle flux for molar conservation. Further, I found that input and output concentrations were not consistent, which I addressed with a modification of the basic QWASI aquivalence model to differentiate between diffusion from water to sediment and from sediment to water. I implemented the diffusion modification and particle conservation constraint to the existing applications. I applied the updated model of lead in Lake Ontario using some parameters from a rate constant study, and to a Lake Ontario basin using a combination of parameters representing a new application. Chapter 3 The updated QWASI aquivalence model was applicable to lead but needed to be further developed for the Ra-226 series, and a method was required to fit parameters for specific applications. I expected that the model would be applicable to Pb-210 using many of the existing parameters and could be extended to Ra-226 and Po-210 by selection of appropriate parameters from existing studies and the literature. I expected that the separate modules could be connected by terms for decay and ingrowth. I developed the Ra-226 model by linking the updated QWASI modules with terms for loss and ingrowth by decay for Ra-226, Pb-210 and Po-210. I assigned parameters to this model from previously published studies of Crystal Lake, Wisconsin; Bickford Pond, Massachusetts; and Clinton River, Michigan; and other sources, and adjusted the parameters in an optimization process developed from the Chapter 2 study. The results indicated that the model was extendable to each of the selected Ra-226 nuclides, and that modules could be linked to account for radioactive decay and ingrowth. The developed method was effective in adjusting parameters to the data in the original studies. Comparison of the Ra-226 model to the original dynamic study models revealed discrepancies, attributed either to the original models missing episodic events, and / or to the inability of the steady-state Ra-226 model to represent the effects of parameter variation by single expected values. Chapter 4 Two hypotheses were investigated in Chapter 4 with the Ra-226 series model developed in Chapter 3. The first question was whether the sedimentation iv proportion of Pb-210 losses from the water in a set of Laurentian lakes was as low as estimated in a previous study (CORNETT, 1984). The second question was whether water and sediment measurements of Judge Sissons Lake at the proposed Nunavut mine site (GUERIN, 2012) indicated a watershed contribution to Pb-210 and Po-210 concentrations. I augmented the Laurentian lakes study data with measurements of water from local streams. I selected sample locations, collected samples and with Soroush Fard I performed wet chemistry operations in the A. E. Lalonde actinide laboratory at the University of Ottawa under the direction of Dr. Robert Cornett. Dr. Cornett performed the alpha spectrometry measurements and Cole MacDonald and Dr. Barbara Francisco performed the Inductively-Coupled Plasma Source Mass Spectrometry (ICP-MS) measurements. I applied the Ra-226 model to the original studies using data from these and other sources. I used the Ra-226 model to estimate lake process rates in the original studies. The sedimentation rates in the Laurentian lakes were concluded to be higher than originally estimated: above 85% in five of the seven lakes. I concluded that the watershed was the source of most of the Pb-210 and Po-210 in Judge Sissons Lake water and sediment, and further that a significant proportion from the watershed may originate in the ground. v Contents Abstract ........................................................................................................ ii Acknowledgements ....................................................................................... iii Statement of Originality ................................................................................. iv Contents ...................................................................................................... vi Abbreviations .............................................................................................. xiv 1 Introduction ............................................................................................
Load more

Recommended publications
  • Newsletterlake Kashagawigamog Organization
    WINTER 2019 NEWSLETTERLake Kashagawigamog Organization THE BEAUTY OF WINTER ON KASHAGAWIGAMOG! Lake Kashagawigamog Organization LAKE KASHAGAWIGAMOG ORGANIZATION NEWSLETTER LAKE KASHAGAWIGAMOG ORGANIZATION NEWSLETTER Greetings From The President LKO Annual SEPTIC Winter 2019 INSPECTIONS As autumn fades and winter arrives it is time to reflect on the FOCA, and local politicians to handle General summer of 2019 on Lake Kashagawigamog. The ice finally the many issues relating to the lake. receded at the beginning of May and after a wet spring we We need your help! First, we need you to Meeting The preservation of our natural environment is headed into a drought which meant sunny weekends through speak to your friends and neighbours on most of the summer. Good planning and water management an endeavour that we all share. To this end it the lake to get them to become members of the LKO. Together we will be the small individual efforts that will resulted in us having above average water levels for the season. have a more powerful voice to get things done. SATURDAY JUNE 27, 2020 make the difference, natural shorelines and The LKO had a busy summer. We started with a very successful Second, we need volunteers. They say that many hands make responsible management of our onsite Love your Lake Seminar, our Annual General Meeting, a Cottage 9:00 A.M. light work. Well, we have light work but we need more hands to wastewater. The little steps can pay big Succession Planning seminar with Soyers Lake and FOCA (www. get it done. We want to continue to put on educational and fun Location: To Be Determined foca.on.ca), and another successful Kash Bash.
    [Show full text]
  • Miskwabi Area Watershed Plan * Are Unique in That They Form the Head Waters of the Burnt River System
    ATVing MISKWABI Litter Waterskiing AREA Acid Rain Motor Swimming WATERSHED Canoeing Boating PLAN Renting Roads Logging An Integral Vision for the Fishing Invasive Species Lakes of Long, Miskwabi, Negaunee and Wenona Hunting Water Nutrients • Everything interconnects. Levels Hiking • Everything affects every other thing. Wildlife Forests Streams Septic • Everything brings change to Systems all. Shorelines • Everything influences the Global entire web of the watershed. Warming Personal Watercraft Nothing is separate! Snowmobiling TABLE OF CONTENTS INTRODUCTION................................................... 2 PHYSICAL ELEMENTS ............................................. 16 SOILS ............................................................................ 16 VALUES AND MISSION ................................................. 4 MINERALS & AGGREGATES .......................................... 16 THE WATERSHED PLAN SURVEY ............................... 4 STEEP SLOPES............................................................... 16 MISSION STATEMENT ............................................... 5 NARROW WATER BODIES ............................................ 16 SUMMARY OF STEWARDSHIP ACTION PLAN ....... 6 SOCIAL ELEMENTS ................................................. 48 LAKE DESCRIPTION ............................................ 10 SOCIAL CULTURE .......................................................... 48 HISTORY .................................................................. 10 TRANQUILITY & NIGHT SKIES ......................................
    [Show full text]
  • Trent Assessment Report
    TRENT CONSERVATION COALITION SOURCE PROTECTION REGION Approved Trent Assessment Report Approved October 1, 2014 Volume 1 of 3 Effective Janurary 1, 2015 Updated February 15, 2018 Trent Source Protection Areas: Crowe Valley Source Protection Area Kawartha-Haliburton Source Protection Area Lower Trent Source Protection Area Otonabee-Peterborough Source Protection Area Made possible through the support of the Government of Ontario www.trentsourceprotection.on.ca This Assessment Report was prepared on behalf of the Trent Conservation Coalition Source Protection Committee under the Clean Water Act, 2006. TRENT CONSERVATION COALITION SOURCE PROTECTION COMMITTEE Jim Hunt (Chair) Municipal The Trent Conservation Coalition Source Dave Burton Protection Committee is a locally based Rob Franklin (Bruce Craig to June 2011) committee, comprised of 28 Dave Golem representatives from municipal Rosemary Kelleher‐MacLennan government, First Nations, the Gerald McGregor commercial/industrial/agriculture sectors, Mary Smith and other interests. The Committee’s Richard Straka ultimate role is to develop a Source Protection Plan that establishes policies for Commercial/Industrial preventing, reducing, or eliminating threats Monica Berdin, Recreation/Tourism to sources of drinking water. In developing Edgar Cornish, Agriculture the plan, the committee members are Kerry Doughty, Aggregate/Mining Robert Lake, Economic Development committed to the following: Glenn Milne, Agriculture . Basing policies on the best available Bev Spencer, Agriculture science, and
    [Show full text]
  • Eat Play Stay
    Canoe Longspur Source Lake Canisbay Lake Lake Lake Jack Lake Bonita Lake Smoke Tanamakoon Lake of Tea Lake Lake Lake Cache Two Rivers Little Island Lake Provoking Swan Lake Lake Lake Norway 1 Lake Fork Lake Ragged Lake 3 3 2 4 Oxtongue Lake Oxtongue Lake Algonquin To North Bay Highlands (125 km) Clinto ALGONQUIN Lake Selected Features Tock Lake 1 Point of Interest 5 2 Kawagama 1 Trail Head 6 Lake 127 Lake of Bays Dorset 1 1 Point of Interest & Trail Head PROVINCIAL Raven HALIBURTON FOREST Lake FROST CENTRE AND WILDLIFE RESERVE AREA Little Kennisis Lake Red Pine 5 Nunikani 7 Lake Lake Kennisis Lake Macdonald Lake Follow to Sherborne Lake St. Nora Little PARK Highway 62 South 8 Lake Big Hawk 9 Redstone continue to Lake Lake Marsden Lake 8 Peterson Rd Little Hawk turns into Halls Lake Kabakwa Lake 4 County Road 10 Lake Redstone (Elephant Lake Rd) Halls Percy Kushog Lake Lake (55 km) POKER LAKES Lake Fort Irwin AREA Lake 58 mins 12 Haliburton 10 West Guilford Lake Moose Lake 11 Maple Kingscote Lake Big East Pine Eagle Lake Lake Eagle Lake Lake Beech 26 Lake Boshkung Lake Lake 10 22 9 13 Little Boshkung Carnarvon Crotchet Lake 6 Lake 14 Benoir Lake Twelve Mile Dysart et al 6 2 Lake 16 Minden Fishtail Lake 1 23 Soyers 7 Follow to Hills Lake g Haliburton Horseshoe mo Spruce Lake Highway 62 North ga Drag Lake Lake wi Elephant Lake 25 ga Kennibik Lake Mountain a 15 continue to Big Trout ash Lake ke K 27 17 Lake 18 La Highway 127 North 18 Grace 15 21 Miskwabi Farquhar follow to Lake 20 22 Lake Lake Harcourt Bob Lake Highway 60 West Canning Donald
    [Show full text]
  • The Beautiful Lake: a Bi‐National Biodiversity Conservation Strategy for Lake Ontario
    The Beautiful Lake A Bi‐national Biodiversity Conservation Strategy for Lake Ontario Prepared by the Lake Ontario Bi‐national Biodiversity Conservation Strategy Working Group In cooperation with the U.S. – Canada Lake Ontario Lakewide Management Plan April 2009 ii The name "Ontario" comes from a native word, possibly "Onitariio" or "Kanadario", loosely translated as "beautiful" or "sparkling" water or lake. (Government of Ontario 2008) The Beautiful Lake: A Bi‐national Biodiversity Conservation Strategy for Lake Ontario April 2009 Prepared by: Lake Ontario Biodiversity Strategy Working Group In co‐operation with: U.S. – Canada Lake Ontario Lake‐wide Management Plan Acknowledgements Funding for this initiative was provided by the Great Lakes National Program Office and Region 2 of the U.S. Environmental Protection Agency, the Canada‐Ontario Agreement Respecting the Great Lakes Basin Ecosystem, The Nature Conservancy and The Nature Conservancy of Canada. This conservation strategy presented in this report reflects the input of over 150 experts representing 53 agencies including Conservation Authorities, universities, and NGOs (see Appendix A.1). In particular, the authors acknowledge the guidance and support of the project Steering Committee: Mark Bain (Cornell University), Gregory Capobianco (New York Department of State), Susan Doka (Department of Fisheries and Oceans), Bonnie Fox (Conservation Ontario), Michael Greer (U.S. Army Corps of Engineers), Frederick Luckey (U.S. Environmental Protection Agency), Jim MacKenzie (Ontario Ministry of Natural Resources), Mike McMurtry (Ontario Ministry of Natural Resources), Joseph Makarewicz (SUNY‐Brockport), Angus McLeod (Parks Canada), Carolyn O’Neill (Environment Canada1), Karen Rodriquez (U.S. Environmental Protection Agency) and Tracey Tomajer (New York State Department of Environmental Conservation).
    [Show full text]
  • Sturgeon Lake Watershed Characterization Report
    Sturgeon Lake Watershed Characterization Report 2014 ii STURGEON LAKE WATERSHED CHARACTERIZATION REPORT KAWARTHA CONSERVATION About Kawartha Conservation A plentiful supply of clean water is a key component of our natural infrastructure. Our surface and groundwater resources supply our drinking water, maintain property values, sustain an agricultural industry and support tourism. Kawartha Conservation is the local environmental agency through which we can protect our water and other natural resources. Our mandate is to ensure the conservation, restoration and responsible management of water, land and natural habitats through programs and services that balance human, environmental and economic needs. We are a non-profit environmental organization, established in 1979 under the Ontario Conservation Authorities Act (1946). We are governed by the six municipalities that overlap the natural boundaries of our watershed and voted to form the Kawartha Region Conservation Authority. These municipalities include the City of Kawartha Lakes, Township of Scugog (Region of Durham), Township of Brock (Region of Durham), the Municipality of Clarington (Region of Durham), Township of Cavan Monaghan, and the Municipality of Trent Lakes. iv STURGEON LAKE WATERSHED CHARACTERIZATION REPORT KAWARTHA CONSERVATION Acknowledgements This Watershed Characterization Report was prepared by the Technical Services Department team of Kawartha Conservation with considerable support from other staff. The following individuals have written sections of the report: Alexander
    [Show full text]
  • Real Estate Guide Waterfront
    Issue 8 • August 1, 2013 STATE GUIDE STATE E REAL Real Estate Guide WATERFRONT Marj & John Parish Sales Representatives Living, Loving, CONDOS and Selling Life in the Highlands! RE/MAXNORTH COUNTRY REALTY INC, BROKERAGE 1-800-465-2984 Offi ce: 705-457-1011 Ext: 226 RESIDENTIAL [email protected] www.johnparish.net Home: 705-457-2986 Check out our listings on pg 2 Cover photo courtesy of Elizabeth Thompson LAND Haliburton O ce Minden O ce Kinmount O ce 705-457-2414 705-286-1234 705-488-3077 197 Highland Street 12621 Highway 35 3613 Cty Road 121 www.royallepagelakeso aliburton.ca COTTAGES RE/MAX NORTH COUNTRY Marj & John 1-800-465-2984 REALTY INC, BROKERAGE OFFICE: 705-457-1011 EXT: 226 1-800-465-2984 Offi ce: 705-457-1011 EXT: 226 [email protected] [email protected] Parish WWW.JOHNPARISH.NET www.johnparish.net Home: 705-457-2986 Sales Representatives WELCOME TO SUNSET POINT KENNISIS LAKE - $769,900 Welcome to Sunset Point on prestigious Kennisis Lake! This is it, the perfect blend of peace & serenity. Its all yours on this private, level, Algonquin style paradise on 2 Separate Deeded Lots! The winterized pine interior cottage sits on one lot & a dry boathouse that sleeps 5 on the other. Your cottage is approached via a circular driveway off a year round twp road. Wander through your forest of windswept pines & hemlock to the rocky point waterfront. Go for a swim off the dock in deep crystal clear water or wade in the sandy cove, then sit by the fi re as you watch the most amazing sunsets from your front row seat and enjoy this million dollar big lake view! For a more private sunset experience sit on the upper deck hidden in the trees that was designed specifi cally for sunset viewing.
    [Show full text]
  • AGENDA Regular Council Meeting
    The Municipality of Dysart et al AGENDA Regular Council Meeting August 27, 2012 9:00 a.m. Page 1. ADOPTION OF AGENDA 2. DISCLOSURE OF PECUNIARY INTEREST 3. ADOPTION OF MINUTES FROM PREVIOUS MEETING 5-22 4. FINANCE DEPARTMENT 23 July 2012 Cheque Summary. 24-25 Monthly Revenue/Expense Report as at July 31, 2012. 26 Metered Sewage Report for July 2012. 27-28 s.357/358 Tax Adjustments. 29 Thunder Bay & Area Disaster Relief Fund Re: Request for Financial Support. 5. DELEGATIONS 9:30 a.m. - Gail Stelter, Colourfest Coordinator Re: Colourfest 2012. 10:00 a.m. - Greg Bishop, Items P-14, 15, 18 and 19. 6. FIRE DEPARTMENT 30 Fire Chief Report. 7. ROADS DEPARTMENT 31 Roads Update. 32-35 Roads Needs Study. 36 Ontario Good Roads Association - Alert Re: Minister of Transportation Agrees to "Open Up" MMS Regulations. 8. ENVIRONMENT 37 Recycled Material Report - July 2012. Page 1 of 251 Page 8. ENVIRONMENT 38 Landfill Tipping Fees Report - July. 9. PARKS AND RECREATION DEPARTMENT 39 Parks and Recreation Update. 10. BUILDING AND BY-LAW DEPARTMENT 40 Building Permit Report to July 31, 2012. 41-42 By-law Department Report - July 2012. 11. ADMINISTRATION 43-45 Environment and Green Energy Committee Re: Minutes of July 3, 2012 Meeting. 46-49 Ground Mount Solar Installations. 50-52 Housing and Business Development Committee Re: Minutes of July 3, 2012 Meeting. 53-56 Haliburton Highlands Museum Board Re: a) Minutes of July 3, 2012 Meeting. b) Request for Installation of Railing for Front Ramp. 57-60 Glebe Park Committee Re: Minutes of June 12, 2012 Meeting.
    [Show full text]
  • Lake Plan February 2015
    Gull Lake - Lake Plan February 2015 Acknowledgements Prepared by: The Gull Lake - Lake Plan Steering Committee, consisting of: • Mike Thorne - Committee Chair • Don Drouillard - GLCA Lake Steward • Bruce McClennan-Water Resource Specialist • Richard Newman - GLCA Vice President • Larry Clarke - Councillor, Township of Minden Hills • With assistance from French Planning Services Inc. (Randy French and Julia Sutton) Sponsored by: • Gull Lake Cottagers Association and the generous donations and volunteer time of many individuals. Special thanks to: The following people that helped to gather and present background information for various Sections of this Report: • Heather Reid Past Executive Director, U-Links • Emily Grubb (U-links, Trent University, research project) • Don Drouillard (interpretation of data) • Helga Sonnenberg (in-depth study of lake water and source water, benthics, water quality, and toxicology) • Glen Bonham and David Flowers (fish community) • Dave Bonham (Light Pollution) • Bill Chambers (invasive species and climate change) • Marilyn Hagerman (Lake History) • Don Bell (Boating) • Kathy Hamilton (Physical Elements • Bill Lett (Land Development) • Carol McClennan (Land Use) Also a Special Thanks to Maxxam Laboratories for their analysis of the Benthic and Chemical samples and to Stantec Environmental Consultants for the interpretation of the benthic samples. Also a special thanks to Glen Bonham for his detailed review of the draft document for spelling and grammar. As well, 2 key reference documents that provided background support in the development of the Lake Plan should be noted, namely; the Lake Stewards Handbook (Haliburton Highlands Stewardship Council); and the Lake Planning Handbook for Community Groups (FOCA, French Planning Services, and Haliburton Highlands Stewardship Council). i Table of Contents Page Executive Summary ...................................................................................................................
    [Show full text]
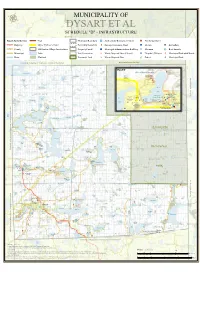
  • Infrastructure
    d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ d[ µ MUNICIPALITY OF DYSART ET AL SCHEDULE "D" - INFRASTRUCTURE d[ Road Jurisdiction Trail Municipal Boundary !Z Auditorium/Recreation Centre «¬ Fire Department 12 (! Highway Major Hydro Corridor Township Boundary ³ Sewage Treatment Plant IH Library . Art Gallery (! County Haliburton Village Service Area Property Parcel ÆX Municipal Administration Building ²¸ Museum d[ Boat Launch Municipal Lake Lot/Concession L Waste Disposal Sites (Closed) ÆP Hospital/Heliport Ý Municipal Park with Beach d[ River Wetland Provincial Park L Waste Disposal Sites 5 SchooÝl Ý Municipal Park Township of Algonquin Highlands, County of Haliburton AlgLonquin Provincial Park INSET Glebe Park Ý Haliburton Highlands Museum ²¸ Kawagama Lake Fleming College - Head Lake Wildcat Lake Haliburton School Trail South of the Arts g Wildcat Slipper Lake n i Lake 5 s i p Head Lake Trail p Stocking i Lake N Havelock Lake Head f o t c Lake i r t ³ s HAVELOCK Haliburton County i Library - D Stuart W. Haliburton Head Lake/ Dysart Branch Grass Baker Highlands Rotary Beach Park Ý Johnson Secondary Sam Lake Elementary Haliburton County IH Drag River Goodwin Lake Ý . School 5 Slick Rail Trail Trail Buckhorn Lake EYRE School d[ Lake Park Rails End 5 J. Douglas A.J. Larue CLYDE Community 5 Hodgson Gallery and Kelly Arts Centre ÆX Centre Lake Elementary !Z Little !Z n School Kennisis Haliburton Curling Club «¬ o t Lake PÆ and Squash Club r u Bone Lake b i l a Red H Ý Pine f Little Eyre Lake Lake o Clean Clean Lake y Kennisis Lake
    [Show full text]
  • Parks Canada Agency Drag Lake Dams Rehabilitation
    PARKS CANADA AGENCY DRAG LAKE DAMS REHABILITATION SPECIFICATIONS Rev. 2 - Issued for Tender June 17, 2016 Prepared by KGS Group TABLE OF CONTENTS Section Number Title 01 11 00 Summary of Work 01 14 00 Work Restrictions 01 22 01 Measurement and Payment 01 31 19 Project Meetings 01 33 00 Submittal Procedures 01 35 29 Health and Safety Requirements 01 35 43 Environmental Procedures 01 45 00 Quality Control 01 52 00 Construction Facilities 01 56 00 Temporary Barriers and Enclosures 01 71 00 Examination and Preparation 01 74 11 Cleaning 01 77 00 Closeout Procedures 01 78 00 Closeout Submittals 02 41 19 Selective Structure Demolition 03 10 00 Concrete Forming and Accessories 03 20 00 Concrete Reinforcing 03 30 00 Cast-in-Place Concrete 03 37 26 Underwater Placed Concrete 05 12 23 Structural Steel 05 51 29 Metal Stairs 31 11 00 Clearing and Grubbing 31 68 13 Post-Tensioned Anchor 35 20 21 Cofferdam and Dewatering 14-1538-002 Section 01 11 00 June 2016 SUMMARY OF WORK Drag Lake Dam Rehabilitation Page 1 Part 1 General 1.1 RELATED REQUIREMENTS .1 Section 01 14 00: Work Restriction .2 Section 01 33 00: Submittal Procedures .3 Section 01 35 43: Environmental Procedures .4 Section 01 45 00: Quality Control .5 Section 01 71 00: Examination and Preparation 1.2 DEFINITIONS .1 Departmental Representative: Parks Canada Agency (PCA) .2 Consultant: KGS Group .3 Contractor: General Contractor who assumes the role of Constructor 1.3 WORK COVERED BY CONTRACT DOCUMENTS .1 Work of this Contract comprises rehabilitation of Drag Lake North Dam and South Dam, located on the Drag River in the Burnt River watershed at the outlet of Outlet Bay (on Drag Lake), near Haliburton, Ontario.
    [Show full text]
  • Water Management Plan
    Water Management Plan For Waterpower Drag Lake Generating Station March 2005 1 WATER MANAGEMENT PLAN FOR WATERPOWER for the Drag Lake Generating Station on the Drag River OMNR Bancroft District, Southern Region Algonquin Power Fund “Canada” Incorporated for the 10-year period April 1, 2005 to March 31, 2015 In submitting this plan, I declare that this water management plan for waterpower has been prepared in accordance with the Ontario Ministry of Natural Resources, Water Management Planning Guidelines for Waterpower, as approved by the Minister of Natural Resources on May 14, 2002. _______________________________________________________________________ David Kerr, Principal, Algonquin Power Fund “Canada” Incorporated Date I have authority to bind the corporation. I certify that this water management plan has been prepared in accordance with the Ontario Ministry of Natural Resources, Water Management Planning Guidelines for Waterpower, as approved by the Minister of Natural Resources on May 14, 2002, and that direction from other sources, relevant policies and other obligations have been considered. I recommend this plan be approved for implementation. ________________________________________________________________________ Monique Rolf von den Baumen-Clark, District Manager, Bancroft District Date Ministry of Natural Resources Approved by: __________________________________ Ron Running, Regional Director, Southern Region Ministry of Natural Resources In 1994, MNR finalized its Statement of Environmental Values (SEV) under the Environmental Bill of Rights. The SEV is a document that describes how the purposes of the EBR are to be considered whenever decisions that might significantly affect the environment are made in the ministry. During the development of this water management plan, the ministry has considered its SEV. 2 This water management plan (WMP) sets out legally enforceable provisions for the management of flows and levels on this river within the values and conditions identified in the WMP.
    [Show full text]