An Introduction to the Standard Model of Particle Physics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Five Common Particles
The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2. -

Fundamentals of Particle Physics
Fundamentals of Par0cle Physics Particle Physics Masterclass Emmanuel Olaiya 1 The Universe u The universe is 15 billion years old u Around 150 billion galaxies (150,000,000,000) u Each galaxy has around 300 billion stars (300,000,000,000) u 150 billion x 300 billion stars (that is a lot of stars!) u That is a huge amount of material u That is an unimaginable amount of particles u How do we even begin to understand all of matter? 2 How many elementary particles does it take to describe the matter around us? 3 We can describe the material around us using just 3 particles . 3 Matter Particles +2/3 U Point like elementary particles that protons and neutrons are made from. Quarks Hence we can construct all nuclei using these two particles -1/3 d -1 Electrons orbit the nuclei and are help to e form molecules. These are also point like elementary particles Leptons We can build the world around us with these 3 particles. But how do they interact. To understand their interactions we have to introduce forces! Force carriers g1 g2 g3 g4 g5 g6 g7 g8 The gluon, of which there are 8 is the force carrier for nuclear forces Consider 2 forces: nuclear forces, and electromagnetism The photon, ie light is the force carrier when experiencing forces such and electricity and magnetism γ SOME FAMILAR THE ATOM PARTICLES ≈10-10m electron (-) 0.511 MeV A Fundamental (“pointlike”) Particle THE NUCLEUS proton (+) 938.3 MeV neutron (0) 939.6 MeV E=mc2. Einstein’s equation tells us mass and energy are equivalent Wave/Particle Duality (Quantum Mechanics) Einstein E -

Introduction to Particle Physics
SFB 676 – Projekt B2 Introduction to Particle Physics Christian Sander (Universität Hamburg) DESY Summer Student Lectures – Hamburg – 20th July '11 Outline ● Introduction ● History: From Democrit to Thomson ● The Standard Model ● Gauge Invariance ● The Higgs Mechanism ● Symmetries … Break ● Shortcomings of the Standard Model ● Physics Beyond the Standard Model ● Recent Results from the LHC ● Outlook Disclaimer: Very personal selection of topics and for sure many important things are left out! 20th July '11 Introduction to Particle Physics 2 20th July '11 Introduction to Particle PhysicsX Files: Season 2, Episode 233 … für Chester war das nur ein Weg das Geld für das eigentlich theoretische Zeugs aufzubringen, was ihn interessierte … die Erforschung Dunkler Materie, …ähm… Quantenpartikel, Neutrinos, Gluonen, Mesonen und Quarks. Subatomare Teilchen Die Geheimnisse des Universums! Theoretisch gesehen sind sie sogar die Bausteine der Wirklichkeit ! Aber niemand weiß, ob sie wirklich existieren !? 20th July '11 Introduction to Particle PhysicsX Files: Season 2, Episode 234 The First Particle Physicist? By convention ['nomos'] sweet is sweet, bitter is bitter, hot is hot, cold is cold, color is color; but in truth there are only atoms and the void. Democrit, * ~460 BC, †~360 BC in Abdera Hypothesis: ● Atoms have same constituents ● Atoms different in shape (assumption: geometrical shapes) ● Iron atoms are solid and strong with hooks that lock them into a solid ● Water atoms are smooth and slippery ● Salt atoms, because of their taste, are sharp and pointed ● Air atoms are light and whirling, pervading all other materials 20th July '11 Introduction to Particle Physics 5 Corpuscular Theory of Light Light consist out of particles (Newton et al.) ↕ Light is a wave (Huygens et al.) ● Mainly because of Newtons prestige, the corpuscle theory was widely accepted (more than 100 years) Sir Isaac Newton ● Failing to describe interference, diffraction, and *1643, †1727 polarization (e.g. -

Read About the Particle Nature of Matter
READING MATERIAL Read About the Particle Nature of Matter PARTICLES OF MATTER DEFINITION Matter is anything that has weight and takes up space. A particle is the smallest possible unit of matter. Understanding that matter is made of tiny particles too small to be seen can help us understand the behavior and properties of matter. To better understand how the 3 states of matter work…. LET’S BREAK IT DOWN! All matter is made of particles that are too small to be seen. Everything you can see and touch is made of matter. It is all the “stuff” in the universe. Things that are not made of matter include energy, and ideas like peace and love. Matter is made up of small particles that are too small to be seen, even with a powerful microscope. They are so small that you would have to put about 100,000 particles in a line to equal the width of a human hair! Page 1 The arrangement of particles determines the state of matter. Particles are arranged and move differently in each state of matter. Solids contain particles that are tightly packed, with very little space between particles. If an object can hold its own shape and is difficult to compress, it is a solid. Liquids contain particles that are more loosely packed than solids, but still closely packed compared to gases. Particles in liquids are able to slide past each other, or flow, to take the shape of their container. Particles are even more spread apart in gases. Gases will fill any container, but if they are not in a container, they will escape into the air. -

Quantum Field Theory*
Quantum Field Theory y Frank Wilczek Institute for Advanced Study, School of Natural Science, Olden Lane, Princeton, NJ 08540 I discuss the general principles underlying quantum eld theory, and attempt to identify its most profound consequences. The deep est of these consequences result from the in nite number of degrees of freedom invoked to implement lo cality.Imention a few of its most striking successes, b oth achieved and prosp ective. Possible limitation s of quantum eld theory are viewed in the light of its history. I. SURVEY Quantum eld theory is the framework in which the regnant theories of the electroweak and strong interactions, which together form the Standard Mo del, are formulated. Quantum electro dynamics (QED), b esides providing a com- plete foundation for atomic physics and chemistry, has supp orted calculations of physical quantities with unparalleled precision. The exp erimentally measured value of the magnetic dip ole moment of the muon, 11 (g 2) = 233 184 600 (1680) 10 ; (1) exp: for example, should b e compared with the theoretical prediction 11 (g 2) = 233 183 478 (308) 10 : (2) theor: In quantum chromo dynamics (QCD) we cannot, for the forseeable future, aspire to to comparable accuracy.Yet QCD provides di erent, and at least equally impressive, evidence for the validity of the basic principles of quantum eld theory. Indeed, b ecause in QCD the interactions are stronger, QCD manifests a wider variety of phenomena characteristic of quantum eld theory. These include esp ecially running of the e ective coupling with distance or energy scale and the phenomenon of con nement. -

B2.IV Nuclear and Particle Physics
B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ...................... -
Pair Energy of Proton and Neutron in Atomic Nuclei
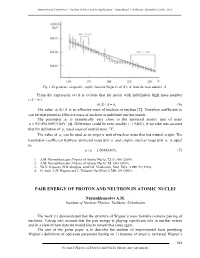
International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again. -

A Young Physicist's Guide to the Higgs Boson
A Young Physicist’s Guide to the Higgs Boson Tel Aviv University Future Scientists – CERN Tour Presented by Stephen Sekula Associate Professor of Experimental Particle Physics SMU, Dallas, TX Programme ● You have a problem in your theory: (why do you need the Higgs Particle?) ● How to Make a Higgs Particle (One-at-a-Time) ● How to See a Higgs Particle (Without fooling yourself too much) ● A View from the Shadows: What are the New Questions? (An Epilogue) Stephen J. Sekula - SMU 2/44 You Have a Problem in Your Theory Credit for the ideas/example in this section goes to Prof. Daniel Stolarski (Carleton University) The Usual Explanation Usual Statement: “You need the Higgs Particle to explain mass.” 2 F=ma F=G m1 m2 /r Most of the mass of matter lies in the nucleus of the atom, and most of the mass of the nucleus arises from “binding energy” - the strength of the force that holds particles together to form nuclei imparts mass-energy to the nucleus (ala E = mc2). Corrected Statement: “You need the Higgs Particle to explain fundamental mass.” (e.g. the electron’s mass) E2=m2 c4+ p2 c2→( p=0)→ E=mc2 Stephen J. Sekula - SMU 4/44 Yes, the Higgs is important for mass, but let’s try this... ● No doubt, the Higgs particle plays a role in fundamental mass (I will come back to this point) ● But, as students who’ve been exposed to introductory physics (mechanics, electricity and magnetism) and some modern physics topics (quantum mechanics and special relativity) you are more familiar with.. -

Baryon and Lepton Number Anomalies in the Standard Model
Appendix A Baryon and Lepton Number Anomalies in the Standard Model A.1 Baryon Number Anomalies The introduction of a gauged baryon number leads to the inclusion of quantum anomalies in the theory, refer to Fig. 1.2. The anomalies, for the baryonic current, are given by the following, 2 For SU(3) U(1)B , ⎛ ⎞ 3 A (SU(3)2U(1) ) = Tr[λaλb B]=3 × ⎝ B − B ⎠ = 0. (A.1) 1 B 2 i i lef t right 2 For SU(2) U(1)B , 3 × 3 3 A (SU(2)2U(1) ) = Tr[τ aτ b B]= B = . (A.2) 2 B 2 Q 2 ( )2 ( ) For U 1 Y U 1 B , 3 A (U(1)2 U(1) ) = Tr[YYB]=3 × 3(2Y 2 B − Y 2 B − Y 2 B ) =− . (A.3) 3 Y B Q Q u u d d 2 ( )2 ( ) For U 1 BU 1 Y , A ( ( )2 ( ) ) = [ ]= × ( 2 − 2 − 2 ) = . 4 U 1 BU 1 Y Tr BBY 3 3 2BQYQ Bu Yu Bd Yd 0 (A.4) ( )3 For U 1 B , A ( ( )3 ) = [ ]= × ( 3 − 3 − 3) = . 5 U 1 B Tr BBB 3 3 2BQ Bu Bd 0 (A.5) © Springer International Publishing AG, part of Springer Nature 2018 133 N. D. Barrie, Cosmological Implications of Quantum Anomalies, Springer Theses, https://doi.org/10.1007/978-3-319-94715-0 134 Appendix A: Baryon and Lepton Number Anomalies in the Standard Model 2 Fig. A.1 1-Loop corrections to a SU(2) U(1)B , where the loop contains only left-handed quarks, ( )2 ( ) and b U 1 Y U 1 B where the loop contains only quarks For U(1)B , A6(U(1)B ) = Tr[B]=3 × 3(2BQ − Bu − Bd ) = 0, (A.6) where the factor of 3 × 3 is a result of there being three generations of quarks and three colours for each quark. -

Introduction to Supersymmetry
Introduction to Supersymmetry Pre-SUSY Summer School Corpus Christi, Texas May 15-18, 2019 Stephen P. Martin Northern Illinois University [email protected] 1 Topics: Why: Motivation for supersymmetry (SUSY) • What: SUSY Lagrangians, SUSY breaking and the Minimal • Supersymmetric Standard Model, superpartner decays Who: Sorry, not covered. • For some more details and a slightly better attempt at proper referencing: A supersymmetry primer, hep-ph/9709356, version 7, January 2016 • TASI 2011 lectures notes: two-component fermion notation and • supersymmetry, arXiv:1205.4076. If you find corrections, please do let me know! 2 Lecture 1: Motivation and Introduction to Supersymmetry Motivation: The Hierarchy Problem • Supermultiplets • Particle content of the Minimal Supersymmetric Standard Model • (MSSM) Need for “soft” breaking of supersymmetry • The Wess-Zumino Model • 3 People have cited many reasons why extensions of the Standard Model might involve supersymmetry (SUSY). Some of them are: A possible cold dark matter particle • A light Higgs boson, M = 125 GeV • h Unification of gauge couplings • Mathematical elegance, beauty • ⋆ “What does that even mean? No such thing!” – Some modern pundits ⋆ “We beg to differ.” – Einstein, Dirac, . However, for me, the single compelling reason is: The Hierarchy Problem • 4 An analogy: Coulomb self-energy correction to the electron’s mass A point-like electron would have an infinite classical electrostatic energy. Instead, suppose the electron is a solid sphere of uniform charge density and radius R. An undergraduate problem gives: 3e2 ∆ECoulomb = 20πǫ0R 2 Interpreting this as a correction ∆me = ∆ECoulomb/c to the electron mass: 15 0.86 10− meters m = m + (1 MeV/c2) × . -

Prospects for Measurements with Strange Hadrons at Lhcb
Prospects for measurements with strange hadrons at LHCb A. A. Alves Junior1, M. O. Bettler2, A. Brea Rodr´ıguez1, A. Casais Vidal1, V. Chobanova1, X. Cid Vidal1, A. Contu3, G. D'Ambrosio4, J. Dalseno1, F. Dettori5, V.V. Gligorov6, G. Graziani7, D. Guadagnoli8, T. Kitahara9;10, C. Lazzeroni11, M. Lucio Mart´ınez1, M. Moulson12, C. Mar´ınBenito13, J. Mart´ınCamalich14;15, D. Mart´ınezSantos1, J. Prisciandaro 1, A. Puig Navarro16, M. Ramos Pernas1, V. Renaudin13, A. Sergi11, K. A. Zarebski11 1Instituto Galego de F´ısica de Altas Enerx´ıas(IGFAE), Santiago de Compostela, Spain 2Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom 3INFN Sezione di Cagliari, Cagliari, Italy 4INFN Sezione di Napoli, Napoli, Italy 5Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom, now at Universit`adegli Studi di Cagliari, Cagliari, Italy 6LPNHE, Sorbonne Universit´e,Universit´eParis Diderot, CNRS/IN2P3, Paris, France 7INFN Sezione di Firenze, Firenze, Italy 8Laboratoire d'Annecy-le-Vieux de Physique Th´eorique , Annecy Cedex, France 9Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology, Kalsruhe, Germany 10Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology, Kalsruhe, Germany 11School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom 12INFN Laboratori Nazionali di Frascati, Frascati, Italy 13Laboratoire de l'Accelerateur Lineaire (LAL), Orsay, France 14Instituto de Astrof´ısica de Canarias and Universidad de La Laguna, Departamento de Astrof´ısica, La Laguna, Tenerife, Spain 15CERN, CH-1211, Geneva 23, Switzerland 16Physik-Institut, Universit¨atZ¨urich,Z¨urich,Switzerland arXiv:1808.03477v2 [hep-ex] 31 Jul 2019 Abstract This report details the capabilities of LHCb and its upgrades towards the study of kaons and hyperons. -

The Standard Model and Beyond Maxim Perelstein, LEPP/Cornell U
The Standard Model and Beyond Maxim Perelstein, LEPP/Cornell U. NYSS APS/AAPT Conference, April 19, 2008 The basic question of particle physics: What is the world made of? What is the smallest indivisible building block of matter? Is there such a thing? In the 20th century, we made tremendous progress in observing smaller and smaller objects Today’s accelerators allow us to study matter on length scales as short as 10^(-18) m The world’s largest particle accelerator/collider: the Tevatron (located at Fermilab in suburban Chicago) 4 miles long, accelerates protons and antiprotons to 99.9999% of speed of light and collides them head-on, 2 The CDF million collisions/sec. detector The control room Particle Collider is a Giant Microscope! • Optics: diffraction limit, ∆min ≈ λ • Quantum mechanics: particles waves, λ ≈ h¯/p • Higher energies shorter distances: ∆ ∼ 10−13 cm M c2 ∼ 1 GeV • Nucleus: proton mass p • Colliders today: E ∼ 100 GeV ∆ ∼ 10−16 cm • Colliders in near future: E ∼ 1000 GeV ∼ 1 TeV ∆ ∼ 10−17 cm Particle Colliders Can Create New Particles! • All naturally occuring matter consists of particles of just a few types: protons, neutrons, electrons, photons, neutrinos • Most other known particles are highly unstable (lifetimes << 1 sec) do not occur naturally In Special Relativity, energy and momentum are conserved, • 2 but mass is not: energy-mass transfer is possible! E = mc • So, a collision of 2 protons moving relativistically can result in production of particles that are much heavier than the protons, “made out of” their kinetic