Electromagnetic System Design for Wireless Power
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Report of Contributions
MT25 Conference 2017 - Timetable, Abstracts, Orals and Posters Report of Contributions https://indico.cern.ch/e/MT25-2017 MT25 Conferenc … / Report of Contributions 3D Electromagnetic Analysis of Tu … Contribution ID: 5 Type: Poster Presentation of 1h45m 3D Electromagnetic Analysis of Tubular Permanent Magnet Linear Launcher Tuesday, 29 August 2017 13:15 (1h 45m) A short stroke and large thrust axial magnetized tubular permanent magnet linear launcher (TPMLL) with non-ferromagnetic rings is presented in this paper. Its 3D finite element (FE) models are estab- lished for sensitivity analyses on some parameters, such as air gap thickness, permanent magnet thickness, permanent magnet width, stator yoke thickness and four types of permanent magnet material, ferrite, NdFeB, AlNiCO5 and Sm2CO17 are conducted to achieve greatest thrust. Then its 2D finite element (FE) models are also established. The electromagnetic thrusts calculated by 2D and 3D finite element method (FEM) and got from prototype test are compared. Moreover, the prototype static and dynamic tests are conducted to verify the 2D and 3D electromagnetic analysis. The FE software FLUX provides the interface with the MATLAB/Simulink to establish combined simulation. To improve the accuracy of the simulation, the combined simulation between the model of the control system in Matlab/Simulink and the 3D FE model of the TPMLL in FLUX is built in this paper. The combined simulation between the control system and the 3D FE modelof the TPMLL is built. A prototype is manufactured according to the final designed dimensions. The photograph of the developed TPMLL prototype with thrust sensor and the magnetic powder brake as the load are shown. -

IEEE/PES Transformers Committee
Transformers Committee Chair: Sue McNelly Vice Chair: Bruce Forsyth Secretary: Ed teNyenhuis Treasurer: Paul Boman Awards Chair/Past Chair: Stephen Antosz Standards Coordinator: Jim Graham IEEE/PES Transformers Committee Spring 2019 Meeting Minutes Anaheim, CA March 24 – 28, 2019 Unapproved (These minutes are on the agenda to be approved at the next meeting in Fall 2019) TABLE OF CONTENTS GENERAL ADMINISTRATIVE ITEMS 1.0 Agenda 2.0 Attendance OPENING SESSION – MONDAY MARCH 25, 2019 3.0 Approval of Agenda and Previous Minutes – Susan McNelly 4.0 Chair’s Remarks & Report – Susan McNelly 5.0 Vice Chair’s Report – Bruce Forsyth 6.0 Secretary’s Report – Ed teNyenhuis 7.0 Treasurer’s Report – Paul Boman 8.0 Awards Report – Stephen Antosz 9.0 Administrative SC Meeting Report – Susan McNelly 10.0 Standards Report – Jim Graham 11.0 Liaison Reports 11.1. CIGRE – Craig Swinderman 11.2. IEC TC14 – Phil Hopkinson 11.3. Standards Coordinating Committee, SCC No. 18 (NFPA/NEC) – David Brender 11.4. Standards Coordinating Committee, SCC No. 4 (Electrical Insulation) – Evanne Wang 11.5. ASTM D27 – Tom Prevost 12.0 Approval of Transformer Committee P&P Manual - Bruce Forsyth 13.0 Hot Topics for the Upcoming – Subcommittee Chairs 14.0 Opening Session Adjournment CLOSING SESSION – THURSDAY MARCH 28, 2019 15.0 Chair’s Remarks and Announcements – Susan McNelly 16.0 Meetings Planning SC Minutes & Report – Tammy Behrens 17.0 Reports from Technical Subcommittees (decisions made during the week) 18.0 Report from Standards Subcommittee (issues from the week) 19.0 -

Eletoz/Vie Patented Sept
Sept. 7, 1926. 1,598,673 O. B. BLACKWELL ET AL SECRECY COMMUNICATION SYSTEM Filed Dec. 18, 1920 R (2AA%aeaeAA 8 eletoz/vie Patented Sept. 7, 1926. 1,598,673 UNITED STATES PATENT office. OTTO B. BLACKWELL, OF GARDEN CITY, NEW YORK; DE Loss K. MARTIN, or oRANGE, NEW JERSEY; AND GILBERT S. VERNAM, OF BROOKLYN, NEw YoRK, AssGNORs TO AMERICAN TELEPHONE AND TELEGRAPH. COMPANY, A CoRFoRATION of NEW YORK, sECREGY coMMUNICATIoN sYSTEM. Application filed December 18, 1920. Serial No. 431,721. This invention relates to a signaling sys pear more fully from the detailed descrip 50 tem wherein signals are transmitted by the tion hereinafter given. agency of a high frequency wave modu The arrangements of the invention are ill lated in accordance with said signals, and lustrated in the accompanying drawing, in more particularly to a signalling system em the figure of which is shown a sendingsta ploying a plurality of high frequency tion of a system embodying the invention. 35 waves. It is the object of the invention to In the arrangements of the drawing are rovide a system of communication where shown four low frequency channels 1, 2, 3 y secret communications between stations and 4 from which the low frequency sig 10 may be had to the end that stations, other nals, such as four telephone messages, may than those designed to receive, may not re be transmitted through modulating appara 60 ceive complete, intelligible signals. tus out over a transmission line L. The Heretofore in certain types of signaling modulating apparatus is shown schemati systems, in which a high frequency wave is cally and includes the modulators M., M., 15 utilized as the agency for transmitting the Me and Ma, with which are associated the signals, he signals have been transmitted high frequency sources A, B, C, and D, 65 by electromagnetic waves of a definite high which are of suitable different frequencies. -

IP 202-1 List of Materials
Changes to the List of Materials August 3, 2021 1. Page be(2.3) a. Added Siemens i. CMR May 6, 2021 1. Page Ugn-2 a. Added Aluma-Form i. ENC Series April 27, 2021 1. Page Ugk-2.2 a. Added Prysmian i. PCT Series (15, 25, 35kV) February 9, 2021 1. Page be(4.3) a. Added Southern States single-phase SSR type recloser. February 4, 2021 1. Pages rp(1), rp(1.2) a. Revised “Cantega” to “Hubbell Power Systems”. b. Added trademark to Reliaguard. December 10, 2020 1. Page ap-2 a. Modified page number from “1.1” to “2”. November 18, 2020 1. Pages an-3 and an(3.1) a. Moved Virginia Transformer from page an(3.1) Conditional to page an-3 Full Acceptance. November 6, 2020 1. Page ae-1 a. Added Celeco i. Catalog Numbers: HSCEL, RPCEL October 26, 2020 1. Page Uhb-1.1 a. Added TE Connectivity i. Catalog Numbers: 25 kV, used with loadbreak connectors (without test point) - ELB-25- 200 series without jacket seal, ELB-25-200-ES series with jacket seal October 23, 2020 1. Page p(1) a. Added TE Connectivity (Raychem) i. Catalog number: TIL Series September 30, 2020 1. Pages a(3), ea(4), ea(5) – Added new Hendrix insulator models. a. Catalog Numbers: HPI-15VTC, HPI-15VTP, HPI-25VTC-02, HPI-35VTC-02, HPI-35VTP-02, HPI-LP-14FS/FA, HPI-LP-16F, HPI-CLP-15, HPI-CLP-17, HPI-CLP-20 July 7, 2020 1. Page cm-2 – Added Aluma-Form, Inc. -

Practical Transformer Handbook
Practical Transformer Handbook Practical Transformer Handbook Irving M. Gottlieb RE. <» Newnes OXFORD BOSTON JOHANNESBURG MELBOURNE NEW DELHI SINGAPORE Newnes An Imprint of Butterworth-Heinemann Linacre House, Jordan Hill, Oxford OX2 8DP 225 Wildwood Avenue, Woburn, MA 01801-2041 A division of Reed Educational and Professional Publishing Ltd S. A member of the Reed Elsevier pic group First published 1998 Transferred to digital printing 2004 © Irving M. Gottlieb 1998 All rights reserved. No part of this publication may be reproduced in any material form (including photocopying or storing in any medium by electronic means and whether or not transiently or incidentally to some other use of this publication) without the written permission of the copyright holder except in accordance with the provisions of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London, England WIP 9HE. Applications for the copyright holder's written permission to reproduce any part of this publication should be addressed to the publishers British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library ISBN 0 7506 3992 X Library of Congress Cataloguing in Publication Data A catalogue record for this book is available from the Library of Congress DLAOTA TREE Typeset by Jayvee, Trivandrum, India Contents Preface ix Introduction xi 1 An overview of transformer sin electrical technology 1 Amber, lodestones, galvanic cells -

19660019609.Pdf
1966019609-002 i 0 • n l _," i i ,, i, i m i "4 VIRGINIA I I .i POLYTECHNIC t ) i INSTITUTE --. i i i i ENGINEERING EXTENSION SERIES CIRCULAR No. 4 YI (In four parts: A,B,C,D) "_ ¢ PART A ._ ! 4 f • zi PROCEEDINGS OF THE CONFERENCE ON -- The Role of 3z""muta' #on" in Space Technology AUGUST 17-21, 1964 Supported by grants from the National Aeronautics and Space Administration and the National Science Foundation; assisted in planning and presentation , by the NASA Langley Rasearch Center. 1966019609-003 ACKNOWLEDGMENTS VPI is indebted to the National Science Foundation for providing funds for travel and expenses for educational personnel attending the conference and to the National Aeronautics and Space Administration (through the • Virginia Associated Research Center) for providing funds for speakers and incidental expenses. VPI is particularly indebted to the Langley Research Center of NASA for assistance in planning the conference and to the NASA in general for providing many of the speakers and session chairmen. The helpful co-operation of Poly-Scientific Division, Litton Precision i Products, Inc. of Blacksburg, for arranging a plant tour showing their facil- ities for manufacturing slip rings and torque motors and for sponsoring the reception before the banquet is also acknowledged, i The conference committee wishes also to express its gratitude to the conference speakers, session chairmen and local personnel who have contri- i ! buted to the success of the meeting. _ The Conference Committee M. L. Collier, Jr., Professor, Engineering Mechanics J. B. Eades, Jr., Head, Aerospace Engineering T. -

Input Transformers
INPUT TRANSFORMERS MANUFACTURE JANUARY 1965 DISCONTINUED (Pile ss Card 1 on Input Transformers) The manufacture of the following input tranformers has been discontinued and it is not considered necessary to maintain cmplete information in the catalogue. For information on codes not listed below, see other cards on input transformers. Code Replaced by Code Replaced by Code Replaced by Code Replaced by 2OOA & B 215A 227C 243B 2olA to T 216A 2288 & B 244A 202A 218B 218G 229A 245A & B 203A to G 218C to F 230A & B 246A 205A to F 218R to N 231A 246C 207A 219A 2328 & B 247B 208A to L 220A 221D 233A & B 247D to H 208M 2408 220B 221D 233C 281A recom. 247K to N 208N to T 221B 224B 2333 & F 2488 208U 231B 221c 224C 233H 272C recm. 250A & B 208W & Y 221D 224A 2335 251A & D 208AA 223B 222A 233L 252B 208AB 223A to D 2348 to D 2538 208AD 224A 234A 2358 2548 208AF to AH 224B 234B 2368 255B to C 209A & B 224C 238A 2553 to H 210A to E 2258 & B 2398 2555 255K 211A to C 2268 240B to J 255K 212A & B 226B <a, 241A & B 256A 212c 618B recom. 226C 233B 241D 2578 213A to C 226D to H 2428 242B 2588 (a) Replaced by a 634B together with one PlZA710 adapter, one P16A771 instruction sheet, form Pl11869 screws and four P242132 washers. INPUT TRANSFORMERS JAUUAK!l 1965 I (File as Card 2 on In1 put Transformers) I Coda Replaced by Code Replaced by Code Replaced by Code Replaced by 259A&B 274A 292D & E 633A 633G 26OAbrB 274C 298A 298B 633B 6331 261A 275A 299B 614A 633D 262A 2JJA to C 600B 638D 263A 279A 601A 6438 DlJ6227 264D 282C 603B 6448 265A to C 285A to D 611A 64JA 64JB 2668 61 B 285G to J 612A 64JC (a> 26JA 285N 613A 65JA 6 B 268A D93983 285B 614A 661B 2698 286A 615A 662A 2JOA to C 28811 2886 61JA 664A 663B 2JOE 288C 618D 669C 2JOF 2705 288D 618B raccm. -

IBM Confidential Field Engineering Education Student Self-Study Course
Field Engineering Education Student Self-Study Course IBM Confidential Field Engineering Education Student Self-Study Course IBM CDnfidential This document contains information of a proprietary nature. ALL INFORMATION CONTAINED HEREIN SHALL BE KEPT IN CONFI DENCE. None of this information shall be divulged to persons other than: IBM employees authorized by the nature of their duties to receive such information or individuals or organizations authorized by the Field Engineering Division in accordance with existing policy regarding release of company information. Common Carrier Facilities for Teleprocessing PREFACE This course is provided to acquaint Customer Engi neers with some of the important concepts of Com mon Carrier equipment and facilities as used in Teleprocessing environment. This course will also provide the Customer Engineer with a permanent reference for these facilities. Address comments concerning the contents of this publication to: IBM Corporation, Field Engineering Education, Dept. 911, Poughkeepsie, N. Y., 12602 Printed March 1966 IBM CONFIDENTIAL CONTENTS SECTION 1. TELEGRAPH SESSION 3, LONG DISTANCE SYSTEMS • 39 Review Questions 40 SESSION 1, TELEGRAPH SYSTEMS 5 Telegraph Principles 6 SESSION 4, CHANNEL FACILITIES. 41 Transmission Methods • 6 Channels Necessary • 41 Functional Units 6 Grades of Channels • 41 Polar Relays 6 Review Questions 43 Junction Boxes 6 Line Arrestor (Heat) Coils 9 SESSION 5, CIRCUIT CHARACTERISTICS • 45 Repeaters 9 Review Questions 47 Representative Type Equipment 11 Basic Telegraph Circuit -

No V. 2, 1943., N
No_v. 2, 1943., N. BOTSFORD 2,333,148 INDUCTANCE APPARATUS Filed June 28, 1941 LEAKAGE MUCH/WE ‘ LEAKAG! _J MGM'TIC INDUCDINCE CORE ,45 A A l 44 4/ LEAKAGE LEA/(46C _ INDUCTZNCE ‘ 57 TRANSMISSION L INE' INVENTOR N. BOTSFORD AT TORNEV Patented Nov. 2, 1943 r 2,333,148 ‘UNITED STATES PATENT OFFICE Nelson Botsi'ord, Rutherford, N. J., assignor to Bell Telephone Laboratories, Incorporated, New York, N. Y., a corporation of New York Application June 28, 1941, Serial No. 400,339 10 Claims. (01. 178-44) ’ ‘This invention relates to inductance appara- . A further object is to simplify the manufac~ tus, ‘and more particularly to inductance appa ture of: inductance apparatus. ratus for transmitting signaling waves extend ing over, a relatively broad band of frequencies ' . A further object is to compensate‘for the leak with substantially uniform attenuation and rel ageinductance of inductance apparatus in so atively low re?ection. v far as such inductance affects re?ection and Carrier current transmission systems are be ' transmission. ‘ ing presently designed withvv higher frequencies Another object is to provide in a system proper to provide a larger number of discrete carrier terminations for apparatus which functions most channels. This means that certain inductance effectively, only when terminated in the imped ance out of and into which such apparatus is apparatus, such as repeating coils and:trans-/ designed to ‘Operate. formers, is 'also being designed to transmit a '; Another'object is to minimize between adja wider band of frequencies. In the design of’ ' such inductance apparatus, one vfactor involves cent transmission lines crosstalk caused by re controlling the re?ection characteristic. -
Telephone Repeater
r . , , -. ~ .. - ' ..- . ,;:· ; ·; .·-~ I ··, ·, .{ ...... - ,. \: ••· .'}f '---:. !\ ' . ' 111-'..!_..,.,,;..;: ...-.. ..... ' ·• , I ~:-U;. '- .~~ ... ~.<-I -~ I r··· i..:'t '.. --~ INSTRUCTION BULLETIN FOR TELEPHONE REPEATER-<P-7 Signal Corps, U. S. Army Order No. 12930 - Phila. - 42 FORT MONMOUTH SIGNAL CORPS PUBLICATIONS AGENCY FOR REFERENCE ONLY DO NOT TAKE FROM THIS ROOM • BY ORDER OF THE DIRECTOR n4- F't. Mon.- J2-4-43-5M--HQ ~~~~~~~~e_ MANUF ACTUBED BY !ntcrnational retepltone ~ J<adio ;Mfg. eorp. UNITED STATES OF AMERICA INSTRUCTION BULLETIN FOR TELEPHONE REPEATER TP-7 Signal Corps, U. S. Army Order No. 12930 - Phila. - 42 MANUFACTURED BY JJtterJtatioJta! retepltoJte .t J(adio ;tlfp. eorp. UNITED STATES OF AMERICA I October 15, 1942 CONTENTS Section Subj ect Page General .................................................................. ....... 2 Mechan ical Description 2. 1 l ~epeate r U nit ............. .................... ............ ................. 2.2 Power U ni t .................................. .. .............................. 2 2.3 !\ ssem b Ie d Units ---- -·- ·····················---·-·--- ········-········-- 2 3 Circuit D escription 3. 1 I ~ cpea ter Unit ................. ............................................. 2 3.2 l)o wer Unit ............................ ...................................... 5 4 O peration 4.1 General .................................................. ........................ 5 4.2 ·Power Connections ..................... ............................... 6 4.3 Line Connections -
Microwave Electronic News Gathering Chapter 3: Television Field Production Z Chapter 4: Telephone Systems and Interfacing Cc
z o Chapter 1: Radio Field Production F- Chapter 2: Microwave Electronic News Gathering Chapter 3: Television Field Production z_ Chapter 4: Telephone Systems and Interfacing cc co cc o a w o w oc mg M1111111 ma 7 t w 6.1 Radio Field Production Jerry Whitaker Editor Broadcast Engineering Magazine Overland Park, Kansas Radio stations have used the remote location is heard at such gatherings, resist the urge to be broadcast for decades to bring the listener an negative when someone asks for a level of per- added sense of realism and excitement. Although formance that is not practical. Hear everyone out. the concept of the remote -as it is better Even though the engineers present at the meetings known -has not changed substantially over the may know that it is impossible to provide every years, the means to accomplish the task has been reporter on the staff with a separate frequency quantum leaps in performance, ease of operation that can be received at the studio from anywhere and reliability. Radio Electronic News Gathering in town, at least listen to what the users would (RENG) systems of today can be configured to like the system to do. The realities of station provide virtually any degree of sophistication re- economics and the laws of physics can be ex- quired by the station. As with any other area of plained after the desires of the participants have broadcasting, the key to a successful RENG sys- been outlined. Many -perhaps most -RENG sys- tem is thoughtful planning. tems were built on a piecemeal basis, as needs dictated and economics allowed. -
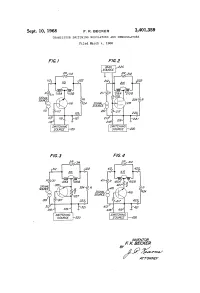
[Aka/QMA T TORNEV 3,401,359 United States Patent 0 ”Ice Patented Sept
Sept. 10, 1968 F. K. BECKER 3,401,359 TRANSISTOR SWITCHING MODULATORS AND DEMODULATORS Filed March 4, 1966 - SIG/ML SOURCE SW/TCH/NG S W/ TCH/NG S OURCE "/20 S OURCE "220 SW/TC‘H/NG SWITCH/N6 soupcg ~320 SOURCE ~420 lNl/ENTOR E K BECKER [aka/QMA T TORNEV 3,401,359 United States Patent 0 ”ice Patented Sept. 10, 1968 1 2 gate according to this invention using a balancing resistor 3,401,359 in series with a switching transistor of the junction type. TRANSISTOR SWITCHING MODULATORS An illustrative embodiment of a switching modulator AND DEMODULATORS ' according to this invention is shown in FIG. 1. This modu Floyd K. Becker, Colts Neck, N.J., assignor to Bell Tele UK lator comprises a bridging resistor 114, a center-tapped phone Laboratories, Incorporated, New York, N.Y., a inductor 115 having matched, mutually coupled sections corporation of New York Filed Mar. 4, 1966, Ser. No. 531,935 115A and 115B, junction transistor 116 having its emitter 11 Claims. (Cl. 332—16) electrode connected to the center tap of inductor 115, a pair of input terminals 112-113 and a pair of output This invention relates to signal modulators of the switch 10 terminals 122-123. Terminals 113 and 123 are connected ing type, and also to modi?cations thereof operable as in common to a ground reference point 121. The col transmission gates. lector electrode of transistor 116, illustrated as the n-p-n Modulators ?nd applications in a large variety of data type, is also connected to reference point 121.