DOCSLIB.ORG

Honoring a Gift from Kumbakonam, Volume 53, Number 6

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Honoring a Gift from Kumbakonam Ken Ono oday was an absolutely This adventure was a pilgrimage to glorious day in Madison, pay homage to Srinivasa Ramanu- Wisconsin. It is Christmas jan, the Indian legend whose con- 2005, and everyone in the gruences, formulas, and identities Thouse is asleep after a long have inspired much of my own work. day of enjoying family, opening pre- This fulfilled a personal journey, one sents, and eating enormous portions of with an unlikely beginning in 1984. mashed potatoes and yule log cake. Yet powerful images keep me The Story of Ramanujan awake. Ramanujan was born on December Thirty-six hours ago I returned 22, 1887, in Erode, a small town from a six-day whirlwind jour- about 250 miles southwest of Chen- ney to a far-off place. I spent nai (formerly known as Madras). forty hours on airplanes, and I He was a Brahmin, a member of endured fourteen hours in cars India’s priestly caste, and as a con- dodging bicycles, rickshaws, sequence he lived his life as a cows, goats, and masses of peo- strict vegetarian. ple on roads severely damaged When Ramanujan was one year by recent flooding. These floods old, he moved to Kumbakonam, a would be blamed1 for at least forty-two small town about 170 miles south of deaths. Despite these hardships and Chennai, where his father Srinivasa bad luck, this adventure exceeded my Bust of Srinivasa was a cloth merchant’s clerk. Kum- lofty expectations. Ramanujan by artist Paul bakonam, which is situated on the I ostensibly travelled to Kum- Granlund. banks of the sacred Kaveri River, bakonam with the purpose of giving a was (and remains today) a cos- lecture on mock theta functions and Maass forms mopolitan center of the rural Indian district of at the International Conference on Number Theory Tanjore in the state of Tamil Nadu. Thanks to the and Mathematical Physics at SASTRA University. I area’s rich soil and tropical climate, rice and sugar could have offered other worthy pretexts: I wanted cane crops thrive. In Ramanujan’s day, Kum- to see my student Karl Mahlburg give his first ple- bakonam had a population of fifty thousand. nary lecture. I wanted to applaud my friends Man- Kumbakonam is one of India’s sacred Hindu jul Bhargava and Kannan Soundararajan (he goes towns. It boasts seventeen Hindu temples (eleven by Sound) as they won a prestigious prize. However, honoring the Hindu god Lord Siva, and six honor- my primary reason was personal, not professional. ing the god Lord Vishnu). The town is perhaps most well-known for its Mahamaham Festival, which Ken Ono is the Solle P. and Margaret Manasse Professor is held every twelve lunar years when the Sun en- of Letters and Science at the University of Wisconsin, Madi- ters the constellation of Aquarius and Jupiter en- son. His email address is [email protected]. ters Leo. Nearly one million Hindu pilgrims de- 1This was reported in The Hindu on December 20, 2005. scend on Kumbakonam for the festival. In a ritual 640 NOTICES OF THE AMS VOLUME 53, NUMBER 6 In July 1909, Ramanujan married nine-year-old meant to absolve sins, pilgrims bathe in the S. Janaki Ammal; it was an arranged marriage. After Mahamaham tank, which symbolizes the waters of a short stay with Ramanujan and his family, Janaki India’s holy rivers. returned to her home to learn domestic skills and As a young boy, Ramanujan was a stellar student. pass time until she reached puberty. Ramanujan He entered Town High School in 1898, and he moved to Madras in 1911 and Janaki joined him in would go on to win many awards there. He was a 1912 to begin their married life. To support them, strong student in all subjects, and he stood out as Ramanujan took a post as a clerk in the account- the school’s best math student. His life took a dra- ing department of the Madras Port Trust. matic turn when a friend loaned him the Govern- Ramanujan continued his research in near iso- ment College library’s copy of G. S. Carr’s Synop- lation. His job at the Port Trust provided a salary sis of Elementary Results in Pure Mathematics. G. H. Hardy, the celebrated Cambridge professor, and left time for mathematics. Despite these cir- later described (see page 3 of [17]) the book as cumstances, his frustration mounted. Although some Indian patrons acknowledged his genius, he …the “synopsis” it professes to be. It was unable to find suitable mentors. Indian math- contains enunciations of 6,165 theo- ematicians did not understand his work. rems, systematically and quite scien- After years of such frustration, Ramanujan tifically arranged, with proofs which are boldly wrote distinguished English mathemati- often little more than cross-references… cians. He first wrote H. F. Baker, and then E. W. Hob- Ramanujan became addicted to mathematics son, both times without success. His letters con- research, and he recorded his findings in note- sisted mostly of bare statements of formal books, imitating Carr’s format. He typically offered identities, recorded without any indication of proof. no proofs of any kind. Based on his education, he Due to his lack of formal training, he claimed some presumably did not understand the obligation known results as his own, and he offered others, mathematicians have for justifying their claims such as his work on prime numbers, which were with proofs. plainly false. In this regard, Hardy would later write Thanks to his exemplary performance at Town (see page xxiv of [16]): High School, Ramanujan won a scholarship to Gov- ernment College. However, by the time he enrolled Ramanujan’s theory of primes was vi- there in 1904, his addiction to mathematics made tiated by his ignorance of the theory of it impossible for him to focus on schoolwork. He a complex variable. It was (so to say) unceremoniously flunked out. He would later get what the theory might be if the Zeta- a second chance, a scholarship to attend function had no complex zeroes. …Ra- Pachaiyappa’s College in Madras. However, math- manujan’s Indian work on primes, and ematics again kept him from his schoolwork, and on all the allied problems of the theory, he flunked out a second time. was definitely wrong. By 1907, the gifted Ramanujan was an academic failure. There was no room for him in India’s sys- Ramanujan’s work on Bernoulli numbers, which tem of higher education. Despite his failures, his he presumably included in his letters, also includes friends and parents supported him. They must an incredible mistake involving explicit numbers. have recognized his genius, for they allowed him The Bernoulli numbers [23] are the rational num- to work on mathematics unabated. Vivid accounts 2 bers B2 = 1/6,B4 = 1/30,... defined by portray Ramanujan hunched over his slate on the B B B porch of his house and in the halls of Sarangapani x cot x = 1 − 2 (2x)2 − 4 (2x)4 − 6 (2x)6 −··· . Temple, working feverishly. 2! 4! 6! ….Ramanujan would sit working on the Ramanujan falsely conjectured (see equation (14) pial (porch) of his house on Sarangapani of [23]) that if n is a positive even number, then the Street, legs pulled into his body, a large numerator of Bn/n, when written in lowest terms, slate spread across his lap, madly scrib- is prime.3 This conjecture is false, as is plainly bling, …When he figured something out, seen by he sometimes seemed to talk to himself, B 174611 283 × 617 smile, and shake his head with plea- 20 = = . sure. 20 6600 23 × 3 × 52 × 11 R. Kanigel (see page 67 of [20]) 2This is a slight departure from the modern definition of the Bernoulli numbers b2n. These numbers are related by n+1 It is said (for example, [3, 20]) that Ramanujan the relation B2n =(−1) b2n . believed that his findings were divine, told to him 3Ramanujan obviously considered 1 to be a prime for in dreams by Namagiri, the goddess of Namakkal. this conjecture. JUNE/JULY 2006 NOTICES OF THE AMS 641 In fact, among the even numbers n less than 2000, Newton. News of his election spread quickly, and Ramanujan’s conjecture holds only for the twenty in India he was hailed as a national hero. numbers Ramanujan grew ill towards the end of his stay 2, 4, 6, 8, 10, 12, 14, 16, 18, 26, 34, 36, in England. One of the main reasons for his de- clining health was malnutrition. He was a vegetar- 38, 42, 74, 114, 118, 396, 674, 1870. ian living in World War I England, a time when al- In view of these facts, it is not surprising that Baker most no one else was a vegetarian. Ramanujan also and Hobson dismissed him as a crank. struggled with the severe change in climate; he Then on January 16, 1913, Ramanujan wrote was not accustomed to English weather. He did not G. H. Hardy, a thirty-five year old analyst and num- have (or did not wear) appropriate clothes to pro- ber theorist at Cambridge University. With his let- tect himself from the elements. These conditions ter he included nine pages of mathematical scrawl. took their toll, and Ramanujan became gravely ill. C. P. Snow elegantly recounted (see pages 30-33 of He was diagnosed with tuberculosis. More recently, [18]) Hardy’s reaction to the letter: hepatic amoebiasis [4, 29], a parasitic infection of One morning in 1913, he (Hardy) found, the liver, has been suggested as the true cause of among the letters on his breakfast table, his illness.
Recommended publications
  • Telephone Numbers

    Telephone Numbers

    DISTRICT DISASTER MANAGEMENT AUTHORITY THANJAVUR IMPORTANT TELEPHONE NUMBERS DISTRICT EMERGENCY OPERATION CENTRE THANJAVUR DISTRICT YEAR-2018 2 INDEX S. No. Department Page No. 1 State Disaster Management Department, Chennai 1 2. Emergency Toll free Telephone Numbers 1 3. Indian Meteorological Research Centre 2 4. National Disaster Rescue Team, Arakonam 2 5. Aavin 2 6. Telephone Operator, District Collectorate 2 7. Office,ThanjavurRevenue Department 3 8. PWD ( Buildings and Maintenance) 5 9. Cooperative Department 5 10. Treasury Department 7 11. Police Department 10 12. Fire & Rescue Department 13 13. District Rural Development 14 14. Panchayat 17 15. Town Panchayat 18 16. Public Works Department 19 17. Highways Department 25 18. Agriculture Department 26 19. Animal Husbandry Department 28 20. Tamilnadu Civil Supplies Corporation 29 21. Education Department 29 22. Health and Medical Department 31 23. TNSTC 33 24. TNEB 34 25. Fisheries 35 26. Forest Department 38 27. TWAD 38 28. Horticulture 39 29. Statisticts 40 30. NGO’s 40 31. First Responders for Vulnerable Areas 44 1 Telephone Number Officer’s Details Office Telephone & Mobile District Disaster Management Agency - Thanjavur Flood Control Room 1077 04362- 230121 State Disaster Management Agency – Chennai - 5 Additional Cheif Secretary & Commissioner 044-28523299 9445000444 of Revenue Administration, Chennai -5 044-28414513, Disaster Management, Chennai 044-1070 Control Room 044-28414512 Emergency Toll Free Numbers Disaster Rescue, 1077 District Collector Office, Thanjavur Child Line 1098 Police 100 Fire & Rescue Department 101 Medical Helpline 104 Ambulance 108 Women’s Helpline 1091 National Highways Emergency Help 1033 Old Age People Helpline 1253 Coastal Security 1718 Blood Bank 1910 Eye Donation 1919 Railway Helpline 1512 AIDS Helpline 1097 2 Meteorological Research Centre S.
  • Kumbakonam Bye-Pass - Land Acquisition Sanctioned - Revised Administrative Sanction Accorded - Orders Issued

    Kumbakonam Bye-Pass - Land Acquisition Sanctioned - Revised Administrative Sanction Accorded - Orders Issued

    ABSTRACT Highways Department - Tamil Nadu Road Sector Project - Kumbakonam bye-pass - Land Acquisition sanctioned - Revised Administrative Sanction accorded - Orders Issued. HIGHWAYS (HN1) DEPARTMENT G.O. Ms. No. 189 Dated: 17-10-2002 Read the following 1. G.O. Ms. No. 533 TPT dated. 23.5.1989 2. G.O..Ms .No.59 Highways (HN1) Department dated 16.3.2001 3. From the Project Director ,Tamil Nadu Road Sector Project letter No.1414/2002 /B Section dated. 23.7.2002. ORDER: In the G.O. first read above the Government have accorded administrative sanction of Rs.40.00 lakhs for acquisition of lands for Kumbakonam bye-pass. 2. In the G.O. Second read above the Government have sanctioned Rs.49.50 Crores for acquisition of lands under Tamil Nadu Road Sector Project . 3. In his letter third read above the Project Director, Tamil Nadu Road Sector Project has stated that the approved Kumbakonam bye-pass alignment starts at km 2/10 of Kumbakonam-Sirkazhi road and ends at km. 129/4 of Kumbakonam-Thanjavur road for a length of 8.20 km. The estimate for Rs.44.00 lakhs was technically sanctioned by Chief Engineer (General). This envisages acquisition of lands of about 26 hectares in 10 villages. Lands were acquired to an extent of 11.05.00 hectares at a cost of Rs.34.58 lakhs in 6 villages. Lands were partly acquired in 4 other villages for an extent of 9.75.50 hectares. The value of these lands of 9.75.50 hectares is Rs.36.15 lakhs.
  • A Life Inspired by an Unexpected Genius

    A Life Inspired by an Unexpected Genius

    Quanta Magazine A Life Inspired by an Unexpected Genius The mathematician Ken Ono believes that the story of Srinivasa Ramanujan — mathematical savant and two-time college dropout — holds valuable lessons for how we find and reward hidden genius. By John Pavlus The mathematician Ken Ono in his office at Emory University in Atlanta. For the first 27 years of his life, the mathematician Ken Ono was a screw-up, a disappointment and a failure. At least, that’s how he saw himself. The youngest son of first-generation Japanese immigrants to the United States, Ono grew up under relentless pressure to achieve academically. His parents set an unusually high bar. Ono’s father, an eminent mathematician who accepted an invitation from J. Robert Oppenheimer to join the Institute for Advanced Study in Princeton, N.J., expected his son to follow in his footsteps. Ono’s mother, meanwhile, was a quintessential “tiger parent,” discouraging any interests unrelated to the steady accumulation of scholarly credentials. This intellectual crucible produced the desired results — Ono studied mathematics and launched a promising academic career — but at great emotional cost. As a teenager, Ono became so desperate https://www.quantamagazine.org/the-mathematician-ken-onos-life-inspired-by-ramanujan-20160519/ May 19, 2016 Quanta Magazine to escape his parents’ expectations that he dropped out of high school. He later earned admission to the University of Chicago but had an apathetic attitude toward his studies, preferring to party with his fraternity brothers. He eventually discovered a genuine enthusiasm for mathematics, became a professor, and started a family, but fear of failure still weighed so heavily on Ono that he attempted suicide while attending an academic conference.
  • SNO APP.No Name Contact Address Reason 1 AP-1 K

    SNO APP.No Name Contact Address Reason 1 AP-1 K

    SNO APP.No Name Contact Address Reason 1 AP-1 K. Pandeeswaran No.2/545, Then Colony, Vilampatti Post, Intercaste Marriage certificate not enclosed Sivakasi, Virudhunagar – 626 124 2 AP-2 P. Karthigai Selvi No.2/545, Then Colony, Vilampatti Post, Only one ID proof attached. Sivakasi, Virudhunagar – 626 124 3 AP-8 N. Esakkiappan No.37/45E, Nandhagopalapuram, Above age Thoothukudi – 628 002. 4 AP-25 M. Dinesh No.4/133, Kothamalai Road,Vadaku Only one ID proof attached. Street,Vadugam Post,Rasipuram Taluk, Namakkal – 637 407. 5 AP-26 K. Venkatesh No.4/47, Kettupatti, Only one ID proof attached. Dokkupodhanahalli, Dharmapuri – 636 807. 6 AP-28 P. Manipandi 1stStreet, 24thWard, Self attestation not found in the enclosures Sivaji Nagar, and photo Theni – 625 531. 7 AP-49 K. Sobanbabu No.10/4, T.K.Garden, 3rdStreet, Korukkupet, Self attestation not found in the enclosures Chennai – 600 021. and photo 8 AP-58 S. Barkavi No.168, Sivaji Nagar, Veerampattinam, Community Certificate Wrongly enclosed Pondicherry – 605 007. 9 AP-60 V.A.Kishor Kumar No.19, Thilagar nagar, Ist st, Kaladipet, Only one ID proof attached. Thiruvottiyur, Chennai -600 019 10 AP-61 D.Anbalagan No.8/171, Church Street, Only one ID proof attached. Komathimuthupuram Post, Panaiyoor(via) Changarankovil Taluk, Tirunelveli, 627 761. 11 AP-64 S. Arun kannan No. 15D, Poonga Nagar, Kaladipet, Only one ID proof attached. Thiruvottiyur, Ch – 600 019 12 AP-69 K. Lavanya Priyadharshini No, 35, A Block, Nochi Nagar, Mylapore, Only one ID proof attached. Chennai – 600 004 13 AP-70 G.
  • Arxiv:1906.07410V4 [Math.NT] 29 Sep 2020 Ainlpwrof Power Rational Ftetidodrmc Ht Function Theta Mock Applications

    Arxiv:1906.07410V4 [Math.NT] 29 Sep 2020 Ainlpwrof Power Rational Ftetidodrmc Ht Function Theta Mock Applications

    MOCK MODULAR EISENSTEIN SERIES WITH NEBENTYPUS MICHAEL H. MERTENS, KEN ONO, AND LARRY ROLEN In celebration of Bruce Berndt’s 80th birthday Abstract. By the theory of Eisenstein series, generating functions of various divisor functions arise as modular forms. It is natural to ask whether further divisor functions arise systematically in the theory of mock modular forms. We establish, using the method of Zagier and Zwegers on holomorphic projection, that this is indeed the case for certain (twisted) “small divisors” summatory functions sm σψ (n). More precisely, in terms of the weight 2 quasimodular Eisenstein series E2(τ) and a generic Shimura theta function θψ(τ), we show that there is a constant αψ for which ∞ E + · E2(τ) 1 sm n ψ (τ) := αψ + X σψ (n)q θψ(τ) θψ(τ) n=1 is a half integral weight (polar) mock modular form. These include generating functions for combinato- rial objects such as the Andrews spt-function and the “consecutive parts” partition function. Finally, in analogy with Serre’s result that the weight 2 Eisenstein series is a p-adic modular form, we show that these forms possess canonical congruences with modular forms. 1. Introduction and statement of results In the theory of mock theta functions and its applications to combinatorics as developed by Andrews, Hickerson, Watson, and many others, various formulas for q-series representations have played an important role. For instance, the generating function R(ζ; q) for partitions organized by their ranks is given by: n n n2 n (3 +1) m n q 1 ζ ( 1) q 2 R(ζ; q) := N(m,n)ζ q = −1 = − − n , (ζq; q)n(ζ q; q)n (q; q)∞ 1 ζq n≥0 n≥0 n∈Z − mX∈Z X X where N(m,n) is the number of partitions of n of rank m and (a; q) := n−1(1 aqj) is the usual n j=0 − q-Pochhammer symbol.
  • Changing Land Use Pattern in Nilgiris Hill Environment Using Geospatial Technology P

    Changing Land Use Pattern in Nilgiris Hill Environment Using Geospatial Technology P

    Available Online at http://www.recentscientific.com International Journal of Recent Scientific International Journal of Recent Scientific Research Research Vol. 6, Issue, 4, pp.3679-3683, April, 2015 ISSN: 0976-3031 RESEARCH ARTICLE CHANGING LAND USE PATTERN IN NILGIRIS HILL ENVIRONMENT USING GEOSPATIAL TECHNOLOGY P. Thirumalai*, P.H. Anand and J.Murugesan ARTICLE INFODepartment of Geography,ABSTRACT Govt. Arts College (A), Kumbakonam, TamilNadu, India Article History: The Nilgiri mountain range in south India is considered unique by anthropologists, geologists, Received 2nd, March, 2015 climatologists, botanists as well as tourists. It has remained a subject of constant study and research over Received in revised form 10th, the last two centuries. Man-nature balance had continued undisturbed in the Nilgiris for thousands of March, 2015 years until the early 19th century when it became a British colony attracting, in due course, various Accepted 4th, April, 2015 developmental activities. Subsequently, the Nilgiris and its popular hill stations emerged as favourite Published online 28th, places for rest and recuperation, game and for raising commercial plantations. In the process, the April, 2015 traditional indigenous crops were replaced by “English” vegetables and then natural forests gave way to commercial plantations of coffee, tea and other exoticspecies of trees. Land use is the term that is used to describe human uses of the land, or immediate actions modifying or converting land cover. It includes Key words: such broad categories as human settlements, protected areas and agriculture. Within those broad Land use, Hill environment, categories are more refined categories, such as urban and rural settlements, irrigated and rainfed fields, geospatial, English vegetables, national parks and forest reserves, and transportation and other infrastructure.
  • UBC Math Distinguished Lecture Series Ken Ono (Emory University)

    UBC Math Distinguished Lecture Series Ken Ono (Emory University)

    PIMS- UBC Math Distinguished Lecture Series Ken Ono (Emory University) Nov 9, 2017 University of British Columbia Room: ESB 2012 Vancouver, BC 3:30pm Polya’s Program for the Riemann Hypothesis and Related Problems In 1927 Polya proved that the Riemann Hypothesis is equivalent to the hyperbolicity of Jensen polynomials for Riemann’s Xi-function. This hyperbolicity has only been proved for degrees d=1, 2, 3. We prove the hyperbolicity of 100% of the Jensen poly- nomials of every degree. We obtain a general theorem which models such polyno- mials by Hermite polynomials. This theorem also allows us to prove a conjecture of Chen, Jia, and Wang on the partition function. This is joint work with Michael Griffin, Larry Rolen, and Don Zagier. KEN ONO is the Asa Griggs Candler Professor of Mathematics at Emory University. He is considered to be an expert in the theory of integer partitions and modular forms. His contributions include several monographs and over 150 research and popular articles in number theory, combinatorics and algebra. He received his Ph.D. from UCLA and has received many awards for his research in number theory, including a Guggenheim Fellowship, a Packard Fellowship and a Sloan Fellowship. He was awarded a Presidential Early Career Award for Science and Engineering (PECASE) by Bill Clinton in 2000 and he was named the National Science Foundation’s Distinguished Teaching Scholar in 2005. He serves as Editor-in-Chief for several journals and is an editor of The Ramanujan Journal. Visit his web page at http://www.mathcs.emory.edu/~ono/ Light refreshments will be served in ESB 4133 from 3:00pm For more details please visit the PIMS Webpage at: https://www.pims.math.ca/scientific-event/171109-pumdcko www.pims.math.ca @pimsmath facebook.com/pimsmath .
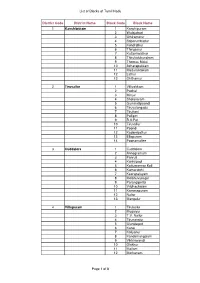
  • List of Blocks of Tamil Nadu District Code District Name Block Code

    List of Blocks of Tamil Nadu District Code District Name Block Code

    List of Blocks of Tamil Nadu District Code District Name Block Code Block Name 1 Kanchipuram 1 Kanchipuram 2 Walajabad 3 Uthiramerur 4 Sriperumbudur 5 Kundrathur 6 Thiruporur 7 Kattankolathur 8 Thirukalukundram 9 Thomas Malai 10 Acharapakkam 11 Madurantakam 12 Lathur 13 Chithamur 2 Tiruvallur 1 Villivakkam 2 Puzhal 3 Minjur 4 Sholavaram 5 Gummidipoondi 6 Tiruvalangadu 7 Tiruttani 8 Pallipet 9 R.K.Pet 10 Tiruvallur 11 Poondi 12 Kadambathur 13 Ellapuram 14 Poonamallee 3 Cuddalore 1 Cuddalore 2 Annagramam 3 Panruti 4 Kurinjipadi 5 Kattumannar Koil 6 Kumaratchi 7 Keerapalayam 8 Melbhuvanagiri 9 Parangipettai 10 Vridhachalam 11 Kammapuram 12 Nallur 13 Mangalur 4 Villupuram 1 Tirukoilur 2 Mugaiyur 3 T.V. Nallur 4 Tirunavalur 5 Ulundurpet 6 Kanai 7 Koliyanur 8 Kandamangalam 9 Vikkiravandi 10 Olakkur 11 Mailam 12 Merkanam Page 1 of 8 List of Blocks of Tamil Nadu District Code District Name Block Code Block Name 13 Vanur 14 Gingee 15 Vallam 16 Melmalayanur 17 Kallakurichi 18 Chinnasalem 19 Rishivandiyam 20 Sankarapuram 21 Thiyagadurgam 22 Kalrayan Hills 5 Vellore 1 Vellore 2 Kaniyambadi 3 Anaicut 4 Madhanur 5 Katpadi 6 K.V. Kuppam 7 Gudiyatham 8 Pernambet 9 Walajah 10 Sholinghur 11 Arakonam 12 Nemili 13 Kaveripakkam 14 Arcot 15 Thimiri 16 Thirupathur 17 Jolarpet 18 Kandhili 19 Natrampalli 20 Alangayam 6 Tiruvannamalai 1 Tiruvannamalai 2 Kilpennathur 3 Thurinjapuram 4 Polur 5 Kalasapakkam 6 Chetpet 7 Chengam 8 Pudupalayam 9 Thandrampet 10 Jawadumalai 11 Cheyyar 12 Anakkavoor 13 Vembakkam 14 Vandavasi 15 Thellar 16 Peranamallur 17 Arni 18 West Arni 7 Salem 1 Salem 2 Veerapandy 3 Panamarathupatti 4 Ayothiyapattinam Page 2 of 8 List of Blocks of Tamil Nadu District Code District Name Block Code Block Name 5 Valapady 6 Yercaud 7 P.N.Palayam 8 Attur 9 Gangavalli 10 Thalaivasal 11 Kolathur 12 Nangavalli 13 Mecheri 14 Omalur 15 Tharamangalam 16 Kadayampatti 17 Sankari 18 Idappady 19 Konganapuram 20 Mac.
  • Thanjavur Sl.No

    Thanjavur Sl.No

    THANJAVUR SL.NO. APPLICATION. NO. NAME AND ADDRESS K.PRIYA D/O KARUNANITHI 9, VATTIPILLAIYAR KOVIL 1 2189 STREET, KUMBAKONAM, THANJAVUR 612001 K.RAMESHKUMAR S/O A.KALIYAMOORTHY 1220METTU ST, 2 2190 MATHI ANNALAGRAHARAM, KUMBAKONAM TK, THANJAVUR 612401 S.SIVAMOHAN S/O S.S RINIVASANATHI 3 2191 PULIYUR POST, KEEZHVELUR T.K, NAGAPATTINAM 611105 N.SRIDHAR SARAVANABAVAN 19/ 3, 18B, T.B. ROAD, 4 2192 THENPATHY, NAGAPATTINAM 609113 K.SARABOSE S/O KULANTHAIVELU 96 SARATHA NAGAR, 5 2193 M.C.ROAD, MANOJIPAT TI, THANJAVUR U.SURESH S/O P.UTHIRAPATHY 6 2194 10,VELLATHI DAL ST, THITTACHERY &POST, NAGAPATTINAM 609703 K.MOHANRAJ S/O V.KATHAN 7 2195 KARUNGANNI POST, KILVELUR TALUK, NAGAPATTINAM B.JAMUNADEVI D/O BALA JOTHINATHAN 8 2196 8 NEW ARCH ST, WEST GATE ROAD, NAGAPATTINAM 611001 K.RAMESHKUMAR S/O A.KALYAMOORTHY 1220 METTU ST, 9 2197 MATHI ANNALAGRAHARA, KUMBAKONAM TK, THANJAVUR 612401 A.HONESTRAJ S/O A.AROKIARAJ SUNAMPUK ALAVAI, 10 2198 THERUMARUNTHUKO, THALAROAD, NAGAPATTINAM 611001 T.ARUL MOOLANGUDI ROAD STREET, 11 2199 ANAIKUPPAM PO, NANNILAM TK, THIRUVARUR 610105 E.SATHISH KUMAR S/O K.ELANGOVAN, AYYANAR KOIL ST, 12 2200 SOMESWARAPURAM PO, PAPANASAM-TK, THANJAVUR B.ARUN S/O BALAKRIS HNAN 13 2201 3/93,AGRAHARA M, 58,ALATHUR POST, NAGAPATTINAM 609604 M.RAVI D/O D.MANICKAM EAST STREET, 14 2202 SANKARANPA NDAL POST, TRANQUEBAR TK, NAGAPATTINAM R.RAJAPRIYA D/O M.RAJAGOPAL 15 2203 T.B.SANATORIYAM, SENGIPATTY POST, THANJAVUR 613401 M.DINESH S/O A.MOHAN 16 2204 99, THULASAPURAM, CO-OPERTATIVE COLONLY, THANJAVUR 613007 T. INDRAKAMATCHI D/O THANGARAJU 17
  • Thanjavur District Industrial Profile 2020-21

    Thanjavur District Industrial Profile 2020-21

    Ministry of Micro, Small and Medium Enterprises Government of India Thanjavur District Industrial Profile 2020-21 Prepared by MSME Development Institute - Chennai Office of the Development Commissioner Ministry of Micro Small and Medium Enterprises Government of India INDEX CHAPTER CONTENT PAGE NO. 1 DISTRICT AT A GLANCE 4 2 INTRODUCTION 10 3 AVAILABLITY OF RESOURCES 16 4 INFRASTRUCTURE FACILITY EXISTING IN 23 THANJAVUR 5 INDUSTRIAL SCENARIO AND MSMEs AT 25 THANJAVUR 6 MICRO SMALL ENTERPRISES- CLUSTER 33 DEVELOPMENT PROGRAMME 7 SWOT ANALYISIS FOR ENTERPRISES 36 DEVELOPMENT 8 INSTITUTIONAL SUPPORT FOR MSMEs 37 9 STEPS TO SET UP ENTERPRISES 44 10 IMPORTANT SCHEMES AND ITS PERFORMANCE 59 11 ADDITIONAL INFORMATION ANNEXURE- ADDRESSESS OF CENTRAL AND STATE GOVT 67 I AUTHORITIES ANNEXURE- IMPORTANT CONTACTS IN THANJAVUR 71 II 2 DISTRICT MAP - THANJAVUR DISTRICT 3 CHAPTER-I THANJAVUR DISTRICT AT A GLANCE 1. PHYSICAL & ADMINISTRATIVE FEATURES Total Geographical Area (Sq.km) 3397 Division Taluks Thanjavur 1 Thanjavur 2 Orathanadu 3 Thiruvaiyaru 4 Budalur Kumbakonam 5 Kumbakonam 6 Papanasam 7 Thiruvidaimaruthur Pattukottai 8 Pattukottai 9 Peravurani Firkas 50 Revenue Villages 906 2. SOIL & CLIMATE Agro-climatic Zone Humid Tropical climate, Zone XI Climate Hot & Humid Soil Type Mainly alluvial 3. LAND UTILISATION [Ha] - (DSH - 2013-14) Total Area Reported 339657 Forest Land 3390 Area Not Available for Cultivation 83879 Permanent Pasture and Grazing Land 1218 Land under Miscellaneous Tree Crops 5337 Cultivable Wasteland 12097 Current Fallow 17943 Other Fallow 28458 Net Sown Area 187335 Total or Gross Cropped Area 267747 Area Cultivated More than Once 80412 Cropping Inensity [GCA/NSA] 143 4 4. RAINFALL & GROUND WATER (DSH - 2013-14) Rainfall [in Normal Actual 2011-12 2012-13 2013-14 mm] 1013 874 757 756 Variation from -13.7% -25.3% -25.4% Normal Availability Net Net Balance of Ground annual annual Water [Ham] recharge draft 73605 52788 20817 5.
  • Sixth Ramanujan Colloquium

    Sixth Ramanujan Colloquium

    University of Florida, Mathematics Department SIXTH RAMANUJAN* COLLOQUIUM by Professor Ken Ono ** Emory University on Adding and Counting Date and Time: 4:05 - 4:55pm, Monday, March 12, 2012 Room: LIT 109 Refreshments: After Colloquium in the Atrium (LIT 339) Abstract: One easily sees that 4 = 3+1 = 2+2 = 2+1+1 = 1+1+1+1, and so we say there are five partitions of 4. What may come as a surprise is that this simple task leads to very subtle and difficult problems in mathematics. The nature of adding and counting has fascinated many of the world's leading mathematicians: Euler, Ramanujan, Hardy, Rademacher, Dyson, to name a few. And as is typical in number theory, some of the most fundamental (and simple to state) questions have remained open. In 2010, with the support of the American Institute for Mathematics and the National Science Foundation, the speaker assembled an international team of researchers to attack some of these problems. Come hear about their findings: new theories which solve some of the famous old questions. * ABOUT RAMANUJAN: Srinivasa Ramanujan (1887-1920), a self-taught genius from South India, dazzled mathematicians at Cambridge University by communicating bewildering formulae in a series of letters. G. H. Hardy invited Ramanujan to work with him at Cambridge, convinced that Ramanujan was a "Newton of the East"! Ramanujan's work has had a profound and wide impact within and outside mathematics. He is considered one of the greatest mathematicians in history. ** ABOUT THE SPEAKER: Ken Ono is one of the top number theorists in the world and a leading authority in the theory of partitions, modular forms, and the work of the Indian genius Srinivasa Ramanujan.
  • Mentoring Graduate Students: Some Personal Thoughts3

    Mentoring Graduate Students: Some Personal Thoughts3

    Early Career the listeners. Like a toddler. He said he tested this when I am not quite sure how I successfully navigated the he was a PhD student. He wanted to know what “ho- stormy seas that defined my early career in mathematics. lomorphic vector bundle” means. So, he went to the What I do know is that I am now fifty-one years old, and math lounge and repeated those three words over and I have enjoyed a privileged career as a research mathe- over again. Now he is an expert in complex geometry. matician. I have had the pleasure of advising thirty PhD • Waking up to Email. Every mentor has a different style. students, with most assuming postdoctoral positions at So does every mentee. A while back, PhD students at top Group 1 institutions. Furthermore, I am proud of the Berkeley complained that they do not get enough at- fact that mathematics continues to play a central role in tention from their advisors. My students think that they their daily lives. receive too much attention from their advisor. A friend How did I make it? Good question. I do know that I once referred to my style as “the samurai method.” It needed the strong support of mentors who kept me afloat involves a barrage of emails, usually sent between 4am along the way. You might know their names: Paul Sally, and 5am. While this is fine for some, it does not work Basil Gordon, and Andrew Granville. I learned a lot from for others. these teachers, and I hope that I have been able to pass their wisdom on to my students of all ages.