DOCSLIB.ORG

Measurements of an FM Receiver in FM Interference

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measurements of an FM Receiver in FM Interference N ITA-REPORT-79-27 Measurements of an FM Receiver in FM Interference J. R. Juroshek u.s. DEPARTMENT OF COMMERCE Juanita M. Kreps, Secretary Henry Geller, Assistant Secretary for Communications and Information October 1979 TABLE OF CONTENTS PAGE LIST OF FIGURES iv LIST OF TABLES v ABSTRACT 1 1. INTRODUCTION 1 2. TEST DESCRIPTION 2 3. TEST RESULTS 7 4. SPECTRUM PHOTOGRAPHS 27 5. SUMMARY AND CONCLUSIONS 31 6 • REFERENCES 33 iii LIST OF FIGURES PAGE Figure 1. Block diagram of equipment. 3 Figure 2. Phase noise from FM generators. 5 Figure 3. Measured performance of an FM receiver 9 in Gaussian noise. Figure 4. Measured performance of an FM receiver 10 with a single FM interferer. Figure 5. Measured performance of an FM receiver 11 with two equal amplitude interferers. Figure 6. Measured performance of an FM receiver 12 with three equal amplitude interferers. Figure 7. Measured performance of an FM receiver 15 with 1, 2 and 3 equal amplitude FM interferers. Peak deviation of all FM generators is e = 3 kHz. Figure 8. Measured performance of an FM receiver 16 with a singLe FM interferer and positi ve and negative frequency offsets~ Peak deviation of generators is '8 = 3 k Hz , Figure 9. Measured performance of an FM receiver with 17 a single FM interferer. Peak frequency deviation of all FM signals is e = 3 kHz. Figure 10. Measured performance of an FM receiver 18 with two FM interferers. Peak frequency deviation of all FM signals is e = 3 kHz. Figure 11. Measurements of SII N required to produce 20 a SINAD = 12 dB witfl a single FM interferer and Gaussian noise. Peak frequency deviation of all FM signals is e = 3 kHz. Figure 12. Measurements of SII N required to produce 21 a SI~D = 12 dB witfl 2 equal amplitude interferers and Gaussian noise. Peak frequency deviation of all FM signal is e = 3 kHz. iv PAGE Figure 13. Threshold of perceptible interference for 23 an FM receiver with a single FM interferer. Peak frequency deviation is 8 = 3 kHz. Figure 14. Threshold of perceptible interference for 24 an FM receiver with equal amplitude FM interferers. Peak frequency deviation is 8 = 3 kHz. Figure 15. Measurements of SINAD as a function of 26 normalized input signal-to-interference ratio for various frequency offsets ~f. Interference is a single FM signal. Peak frequency deviation of all FM generators is 8 = 3 kHz. Figure 16. Spectra of a 171'.8 MHz FM signal modulated 28 with (a) a voice signal and (b) a 400 Hz tone. Peak frequency deviation is e = 3 kHz. Figure 17. Spectra of the audio output from an FM 29 receiver with (a) receiver background noise, (b) Gaussian noise of SiN N = 10 dB, (c) a single FM interferer of S}IIN = 10 dB, and (d) 3 equal amplitude FM interferers of S/IIN = 10 dB. Figure 18. Spectra of the audio output from an FM 30 receiver with a single FM interferer offset in frequency by (a) ~f = 0 kHz, (b) ~f = 4kHz, (c) ~f = 12 kHz and (d) ~f = 24kHz. Peak frequency deviation of all FM signals is 8 = 3 kH~. LIST OF TABLES TABLE 1. Estimates of S/NIN required to produce 13 aSINAD = 12 dB. TABLE 2 • Estimates of SINAD for S/IIN Or 13 S/NIN = 20 dB. TABLE 3. Summary of S/II~ required to produce a 22 SINAD = 12 dB wlth 8 = 3 kHz. v MEASUREMENTS OF AN FM RECEIVER IN FM INTERFERENCE John R. Juroshek* This report investigates the performance of an FM, landrnobile, receiver in FM interference. Measurements are described showing the effects of multiple interfering FM signals as a function of modulation index, signal-to-interference ratio, signal-to-noise ratio, and frequency offset between the victim and interferer. The perfor­ mance of the receiver is measured with various combinations of one to three interfering FM signals. The report also describes the spectra of the audio output during various interference conditions. Key words: frequency modulation; spectrum; interference; communications; land-mobile radio 1. INTRODUCTION An estimate of the performance of an FM system is often based on t he assumption that white Gaussian noise is the factor limiting performance. Increased demands for spectrum, however, are resulting in more instances where interfering signals are the dominant source of degradation. Thus, it becomes increasingly important to understand how an FM receiver behaves in FM interference. This report will discuss the laboratory measurements of a single FM receiver in a co-channel and off-frequency FM interference environment. The effects of one to three independent, interfering, FM signals are measured as a function of modulation index, signal-to-interference ratio, * The author is with u.S. Department of Commerce, Institute for Telecommunication Sciences, National Telecommunications and Information Administration, Boulder, Colorado 80303. signal-to-noise ratio,and frequency offset between victim and interferer. The measurements are limited to a single mobile transceiver that operates on a frequency of 171.8 MHz. The measurements also are limited to laboratory tests with nonfading signals. 2. TEST DESCRIPTION A block diagram of the test setup is shown in Figure 1. As can be seen, the output from four FM signal generators is added in a 50 ohm summing circuit. One of these generators represents the desired signal, while the other three are the interfering signals. Modulation for the FM signal generators is obtained either from the internal sine wave sources within the units or from external voice signals. Each of the external voice modulating signals is independent and is obtained from cassette recordings of spoken phrases. All voice signals are low-pass filtered to eliminate high frequency components f.rom the cassette recorders. These are "Butterworth" filters with a cutoff frequency of 5 kHz and attenuation of 24 dB per octave. White Gaussian noise is included in the tests as shown in the lower part of Figure 1. The output from a noise diode is filtered with a bandpass filter centered at 171.8 MHz and bandwidth of 8 MHz. The filtered noise is amplified in a 40 dB amplifier and sent to the summing circuit. The purpose of the noise filter is simply to prevent overloading of the RF amplifier by the out-of-band noise. The s ummed vs i qnal containing desired and interfering signals, and noise is connected to I t he RF input terminals of the victim FM receiver. All RF connections use double shielded 50 ohm coax. The audio output from the receiver is directed either to a speaker or to a noise and distortion 2 FM Voice "'1 LP SIG FILTER GEN FM Voice"'2 --1 LP I ~I SIG FILTER .. I "S , GEN 1 I 3~ II RF Input \ NOISE & LP FM fM Voice-3 , .... 1 FILTER I -I SIG ~I L H• MOBILE ~ DISTORTION GEN I¥; REC I~ :2 METER w II Audio Output ~ I J fM Voice#4~ LP FILTER SIG I --I GEN NOISE BP RF DIOl! FIL TER AMP Figure 1. Block diagram of equipment. meter whose input is terminated with a noninductive resistor equal to the nominal speaker impedance. Whenever possible, the tests were conducted according to the procedures recommended in EIA Standard RS-204-A (Electronic Industries Association, 1972). The only major deviation from the recommended standard occurs when the FM signal generators are voice modulated. The standard requires that the FM generators be tone-modulated and thus does not define test procedures for voice modulation. Although most of the tests were conducted with tone modulation, it was felt that at least a few tests should use voice modulation to see if there were any major differences. The FM generators were modern units whose output could be frequency locked to insure a stability of better than 5 x 10-8• The accuracy of the counter used to set the generators, on the other hand, was only one part in lOG. Thus, the frequency that the generators are tuned to is known to an accuracy of 500 Hz. This accuracy, however, is sufficient for these tests. One problem that was discovered during the tests is the off-frequency phase noise that is emitted from the FM gener­ ators. The generator specifications state that the phase noise, 20 kHz offset from the carrier, be less than 136 dB below the carrier in a 1 Hz bandwidth. A plot of the phase noise specifications for the FM generators at other frequencies is given in Figure 2. Thus, a receiver with 10 kHz equivalent rectangular bandwidth, at Fe +20 kHz, could expect to receive a signal of approximately P¢ = -136 + 10 log 10 4 dB (1) below the carrier, or P¢ = -96 dB. (2) 4 This, of course, limits the dynamic range over which off­ frequency tests can be made. In practice, the dynamic range of off-frequency testing should be limited to approximately -90 dB below the carrier since the interference from adjacent channel effects must be distinguishable from the - 96 dB phase noise. Thus, throughout the report we shall assume that the dynamic range of the test setup is limited to -90 dB relative to the carrier for frequency offsets of 25 kHz < ~f <30 kHz. .~ -120 I .-5 3: OJ CD (LN -13D £DI -0 .- C c -140 OJ ~ Receiver with (f) OJ ~ ·0 .~ v 7 7 7 7 7 7 10 kHz BW z~ Tuned to 0 OJU -150 tc + 25 kHz (f) o.E .J::. CL -160 fc +IOkHZ +20kHz +30kHz Frequency Figure 2. Phase noise from FM generators. Unfortunately, the test receiver had a selectivity or adjacent channel rejection specification of -100 dBm.
Load more

Recommended publications
  • All You Need to Know About SINAD Measurements Using the 2023
    applicationapplication notenote All you need to know about SINAD and its measurement using 2023 signal generators The 2023A, 2023B and 2025 can be supplied with an optional SINAD measuring capability. This article explains what SINAD measurements are, when they are used and how the SINAD option on 2023A, 2023B and 2025 performs this important task. www.ifrsys.com SINAD and its measurements using the 2023 What is SINAD? C-MESSAGE filter used in North America SINAD is a parameter which provides a quantitative Psophometric filter specified in ITU-T Recommendation measurement of the quality of an audio signal from a O.41, more commonly known from its original description as a communication device. For the purpose of this article the CCITT filter (also often referred to as a P53 filter) device is a radio receiver. The definition of SINAD is very simple A third type of filter is also sometimes used which is - its the ratio of the total signal power level (wanted Signal + unweighted (i.e. flat) over a broader bandwidth. Noise + Distortion or SND) to unwanted signal power (Noise + The telephony filter responses are tabulated in Figure 2. The Distortion or ND). It follows that the higher the figure the better differences in frequency response result in different SINAD the quality of the audio signal. The ratio is expressed as a values for the same signal. The C-MES signal uses a reference logarithmic value (in dB) from the formulae 10Log (SND/ND). frequency of 1 kHz while the CCITT filter uses a reference of Remember that this a power ratio, not a voltage ratio, so a 800 Hz, which results in the filter having "gain" at 1 kHz.
    [Show full text]
  • Next Topic: NOISE
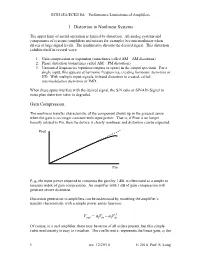
    ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize.
    [Show full text]
  • Smart Innovation, Systems and Technologies
    Smart Innovation, Systems and Technologies Volume 235 Series Editors Robert J. Howlett, Bournemouth University and KES International, Shoreham-by-Sea, UK Lakhmi C. Jain, KES International, Shoreham-by-Sea, UK The Smart Innovation, Systems and Technologies book series encompasses the topics of knowledge, intelligence, innovation and sustainability. The aim of the series is to make available a platform for the publication of books on all aspects of single and multi-disciplinary research on these themes in order to make the latest results available in a readily-accessible form. Volumes on interdisciplinary research combining two or more of these areas is particularly sought. The series covers systems and paradigms that employ knowledge and intelligence in a broad sense. Its scope is systems having embedded knowledge and intelligence, which may be applied to the solution of world problems in industry, the environment and the community. It also focusses on the knowledge-transfer methodologies and innovation strategies employed to make this happen effectively. The combination of intelligent systems tools and a broad range of applications introduces a need for a synergy of disciplines from science, technology, business and the humanities. The series will include conference proceedings, edited collections, monographs, hand- books, reference books, and other relevant types of book in areas of science and technology where smart systems and technologies can offer innovative solutions. High quality content is an essential feature for all book proposals accepted for the series. It is expected that editors of all accepted volumes will ensure that contributions are subjected to an appropriate level of reviewing process and adhere to KES quality principles.
    [Show full text]
  • Receiver Sensitivity and Equivalent Noise Bandwidth Receiver Sensitivity and Equivalent Noise Bandwidth
    11/08/2016 Receiver Sensitivity and Equivalent Noise Bandwidth Receiver Sensitivity and Equivalent Noise Bandwidth Parent Category: 2014 HFE By Dennis Layne Introduction Receivers often contain narrow bandpass hardware filters as well as narrow lowpass filters implemented in digital signal processing (DSP). The equivalent noise bandwidth (ENBW) is a way to understand the noise floor that is present in these filters. To predict the sensitivity of a receiver design it is critical to understand noise including ENBW. This paper will cover each of the building block characteristics used to calculate receiver sensitivity and then put them together to make the calculation. Receiver Sensitivity Receiver sensitivity is a measure of the ability of a receiver to demodulate and get information from a weak signal. We quantify sensitivity as the lowest signal power level from which we can get useful information. In an Analog FM system the standard figure of merit for usable information is SINAD, a ratio of demodulated audio signal to noise. In digital systems receive signal quality is measured by calculating the ratio of bits received that are wrong to the total number of bits received. This is called Bit Error Rate (BER). Most Land Mobile radio systems use one of these figures of merit to quantify sensitivity. To measure sensitivity, we apply a desired signal and reduce the signal power until the quality threshold is met. SINAD SINAD is a term used for the Signal to Noise and Distortion ratio and is a type of audio signal to noise ratio. In an analog FM system, demodulated audio signal to noise ratio is an indication of RF signal quality.
    [Show full text]
  • Noise Is Widespread
    NoiseNoise A definition (not mine) Electrical Noise S. Oberholzer and E. Bieri (Basel) T. Kontos and C. Hoffmann (Basel) A. Hansen and B-R Choi (Lund and Basel) ¾ Electrical noise is defined as any undesirable electrical energy (?) T. Akazaki and H. Takayanagi (NTT) E.V. Sukhorukov and D. Loss (Basel) C. Beenakker (Leiden) and M. Büttiker (Geneva) T. Heinzel and K. Ensslin (ETHZ) M. Henny, T. Hoss, C. Strunk (Basel) H. Birk (Philips Research and Basel) Effect of noise on a signal. (a) Without noise (b) With noise ¾ we like it though (even have a whole conference on it) National Center on Nanoscience Swiss National Science Foundation 1 2 Noise may have been added to by ... Introduction: Noise is widespread Noise (audio, sound, HiFi, encodimg, MPEG) Electrical Noise Noise (industrial, pollution) Noise (in electronic circuits) Noise (images, video, encoding) Noise (environment, pollution) it may be in the “source” signal from the start Noise (radio) it may have been introduced by the electronics Noise (economic => theory of pricing with fluctuating it may have been added to by the envirnoment source terms) it may have been generated in your computer Noise (astronomy, big-bang, cosmic background) Noise figure Shot noise Thermal noise for the latter, e.g. sampling noise Quantum noise Neuronal noise Standard quantum limit and more ... 3 4 Introduction: Noise is widespread Introduction (Wikipedia) Noise (audio, sound, HiFi, encodimg, MPEG) Electronic Noise (from Wikipedia) Noise (industrial, pollution) Noise (in electronic circuits) Noise (images, video, encoding) Electronic noise exists in any electronic circuit as a result of random variations in current or voltage caused by the random movement of the Noise (environment, pollution) electrons carrying the current as they are jolted around by thermal energy.energy Noise (radio) The lower the temperature the lower is this thermal noise.
    [Show full text]
  • Understanding Noise Figure
    Understanding Noise Figure Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul One of the most frequently discussed forms of noise is known as Thermal Noise. Thermal noise is a random fluctuation in voltage caused by the random motion of charge carriers in any conducting medium at a temperature above absolute zero (K=273 + °Celsius). This cannot exist at absolute zero because charge carriers cannot move at absolute zero. As the name implies, the amount of the thermal noise is to imagine a simple resistor at a temperature above absolute zero. If we use a very sensitive oscilloscope probe across the resistor, we can see a very small AC noise being generated by the resistor. • The RMS voltage is proportional to the temperature of the resistor and how resistive it is. Larger resistances and higher temperatures generate more noise. The formula to find the RMS thermal noise voltage Vn of a resistor in a specified bandwidth is given by Nyquist equation: Vn = 4kTRB where: k = Boltzmann constant (1.38 x 10-23 Joules/Kelvin) T = Temperature in Kelvin (K= 273+°Celsius) (Kelvin is not referred to or typeset as a degree) R = Resistance in Ohms B = Bandwidth in Hz in which the noise is observed (RMS voltage measured across the resistor is also function of the bandwidth in which the measurement is made). As an example, a 100 kΩ resistor in 1MHz bandwidth will add noise to the circuit as follows: -23 3 6 ½ Vn = (4*1.38*10 *300*100*10 *1*10 ) = 40.7 μV RMS • Low impedances are desirable in low noise circuits.
    [Show full text]
  • MT-004: the Good, the Bad, and the Ugly Aspects of ADC Input Noise-Is
    MT-004 TUTORIAL The Good, the Bad, and the Ugly Aspects of ADC Input Noise—Is No Noise Good Noise? by Walt Kester INTRODUCTION All analog-to-digital converters (ADCs) have a certain amount of "input-referred noise"— modeled as a noise source connected in series with the input of a noise-free ADC. Input-referred noise is not to be confused with quantization noise which only occurs when an ADC is processing an ac signal. In most cases, less input noise is better, however there are some instances where input noise can actually be helpful in achieving higher resolution. This probably doesn't make sense right now, so you will just have to read further into this tutorial to find out how SOME noise can be GOOD noise. INPUT-REFERRED NOISE (CODE TRANSITION NOISE) Practical ADCs deviate from ideal ADCs in many ways. Input-referred noise is certainly a departure from the ideal, and its effect on the overall ADC transfer function is shown in Figure 1. As the analog input voltage is increased, the "ideal" ADC (shown in Figure 1A) maintains a constant output code until the transition region is reached, at which point the output code instantly jumps to the next value and remains there until the next transition region is reached. A theoretically perfect ADC has zero "code transition" noise, and a transition region width equal to zero. A practical ADC has certain amount of code transition noise, and therefore a transition region width that depends on the amount of input-referred noise present (shown in Figure 1B).
    [Show full text]
  • Clock Jitter Effects on the Performance of ADC Devices
    Clock Jitter Effects on the Performance of ADC Devices Roberto J. Vega Luis Geraldo P. Meloni Universidade Estadual de Campinas - UNICAMP Universidade Estadual de Campinas - UNICAMP P.O. Box 05 - 13083-852 P.O. Box 05 - 13083-852 Campinas - SP - Brazil Campinas - SP - Brazil [email protected] [email protected] Karlo G. Lenzi Centro de Pesquisa e Desenvolvimento em Telecomunicac¸oes˜ - CPqD P.O. Box 05 - 13083-852 Campinas - SP - Brazil [email protected] Abstract— This paper aims to demonstrate the effect of jitter power near the full scale of the ADC, the noise power is on the performance of Analog-to-digital converters and how computed by all FFT bins except the DC bin value (it is it degrades the quality of the signal being sampled. If not common to exclude up to 8 bins after the DC zero-bin to carefully controlled, jitter effects on data acquisition may severely impacted the outcome of the sampling process. This analysis avoid any spectral leakage of the DC component). is of great importance for applications that demands a very This measure includes the effect of all types of noise, the good signal to noise ratio, such as high-performance wireless distortion and harmonics introduced by the converter. The rms standards, such as DTV, WiMAX and LTE. error is given by (1), as defined by IEEE standard [5], where Index Terms— ADC Performance, Jitter, Phase Noise, SNR. J is an exact integer multiple of fs=N: I. INTRODUCTION 1 s X = jX(k)j2 (1) With the advance of the technology and the migration of the rms N signal processing from analog to digital, the use of analog-to- k6=0;J;N−J digital converters (ADC) became essential.
    [Show full text]
  • Analog-To-Digital Conversion Revolutionized by Deep Learning Shaofu Xu1, Xiuting Zou1, Bowen Ma1, Jianping Chen1, Lei Yu1, Weiwen Zou1, *
    Analog-to-digital Conversion Revolutionized by Deep Learning Shaofu Xu1, Xiuting Zou1, Bowen Ma1, Jianping Chen1, Lei Yu1, Weiwen Zou1, * 1State Key Laboratory of Advanced Optical Communication Systems and Networks, Department of Electronic Engineering, Shanghai Jiao Tong University, Shanghai 200240, China. *Correspondence to: [email protected]. Abstract: As the bridge between the analog world and digital computers, analog-to-digital converters are generally used in modern information systems such as radar, surveillance, and communications. For the configuration of analog- to-digital converters in future high-frequency broadband systems, we introduce a revolutionary architecture that adopts deep learning technology to overcome tradeoffs between bandwidth, sampling rate, and accuracy. A photonic front-end provides broadband capability for direct sampling and speed multiplication. Trained deep neural networks learn the patterns of system defects, maintaining high accuracy of quantized data in a succinct and adaptive manner. Based on numerical and experimental demonstrations, we show that the proposed architecture outperforms state-of- the-art analog-to-digital converters, confirming the potential of our approach in future analog-to-digital converter design and performance enhancement of future information systems. bandwidth, sampling rate, and accuracy (dynamic range) From the advent of digital processing and the von remains a challenge for all existing ADC architectures. Neumann computing scheme, the continuous world has become discrete by use of analog-to-digital converters Deep learning techniques involve a family of data (ADCs). Discrete digital signals are easier to process, processing algorithms that use deep neural networks to store, and display; thus, they are integral to modern manipulate data (10).
    [Show full text]
  • Measurement of Delta-Sigma Converter
    FACULTY OF ENGINEERING AND SUSTAINABLE DEVELOPMENT . Measurement of Delta-Sigma Converter Liu Xiyang 06/2011 Bachelor’s Thesis in Electronics Bachelor’s Program in Electronics Examiner: Niclas Bjorsell Supervisor: Charles Nader 1 2 Liu Xiyang Measurement of Delta-Sigma Converter Acknowledgement Here, I would like to thank my supervisor Charles. Nader, who gave me lots of help and support. With his guidance, I could finish this thesis work. 1 Liu Xiyang Measurement of Delta-Sigma Converter Abstract With today’s technology, digital signal processing plays a major role. It is used widely in many applications. Many applications require high resolution in measured data to achieve a perfect digital processing technology. The key to achieve high resolution in digital processing systems is analog-to-digital converters. In the market, there are many types ADC for different systems. Delta-sigma converters has high resolution and expected speed because it’s special structure. The signal-to-noise-and-distortion (SINAD) and total harmonic distortion (THD) are two important parameters for delta-sigma converters. The paper will describe the theory of parameters and test method. Key words: Digital signal processing, ADC, delta-sigma converters, SINAD, THD. 2 Liu Xiyang Measurement of Delta-Sigma Converter Contents Acknowledgement................................................................................................................................... 1 Abstract ..................................................................................................................................................
    [Show full text]
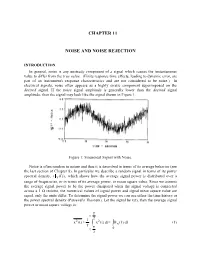
  • Chapter 11 Noise and Noise Rejection
    CHAPTER 11 NOISE AND NOISE REJECTION INTRODUCTION In general, noise is any unsteady component of a signal which causes the instantaneous value to differ from the true value. (Finite response time effects, leading to dynamic error, are part of an instrument's response characteristics and are not considered to be noise.) In electrical signals, noise often appears as a highly erratic component superimposed on the desired signal. If the noise signal amplitude is generally lower than the desired signal amplitude, then the signal may look like the signal shown in Figure 1. Figure 1: Sinusoidal Signal with Noise. Noise is often random in nature and thus it is described in terms of its average behavior (see the last section of Chapter 8). In particular we describe a random signal in terms of its power spectral density, (x (f )) , which shows how the average signal power is distributed over a range of frequencies, or in terms of its average power, or mean square value. Since we assume the average signal power to be the power dissipated when the signal voltage is connected across a 1 Ω resistor, the numerical values of signal power and signal mean square value are equal, only the units differ. To determine the signal power we can use either the time history or the power spectral density (Parseval's Theorem). Let the signal be x(t), then the average signal power or mean square voltage is: T t 2 221 x(t) x(t)dtx (f)df (1) T T t 0 2 11-2 Note: the bar notation, , denotes a time average taken over many oscillations of the signal.
    [Show full text]
  • Impact of PLL Jitter to GSPS ADC's SNR and Performance Optimization
    www.ti.com Table of Contents Application Report Impact of PLL Jitter to GSPS ADC's SNR and Performance Optimization Neeraj Gill, Salvo Finocchiaro ABSTRACT Jitter noise contributed by the clock source (frequency synthesizer or phase-locked loop (PLL)) has a big impact on the performance of new generation high-performance Gsps analog-to-digital converters (ADC). Both in-band and out of-band noise performance of the PLL impact the ADC signal-to-noise ratio (SNR), and consequently the effective resolution of the ADC (ENOB). The noise contributed by the PLL can be reduced by operating the PLL Phase Frequency Detector (PFD) at higher frequencies, reducing the input -output multiplication factor N, and using a bandpass filter to reduce far-out noise (or noise floor). This application note describes how to estimate the jitter requirements, translate that into a PLL phase noise requirement, and determine (recommending) the filter bandwidth needed to minimize the SNR performance degradation due to the clocking source. While this analysis is generic and applies to any PLL and ADC, a specific example will be provided by using TI LMX2594 high performance PLL and ADC12DJ5200 12-bit, 5-GSPS ADC. Table of Contents 1 PLL Phase Noise and RMS Jitter...........................................................................................................................................2 2 ADC SNR and Jitter Impact....................................................................................................................................................4
    [Show full text]