DOCSLIB.ORG

Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces DEGREE PROJECT IN MATHEMATICS, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2020 Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ENGINEERING SCIENCES Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON Degree Projects in Mathematical Statistics (30 ECTS credits) Master's Programme in Applied and Computational Mathematics (120 credits) KTH Royal Institute of Technology year 2020 Supervisor at Nasdaq Technology AB: Sebastian Lindberg Supervisor at KTH: Fredrik Viklund Examiner at KTH: Fredrik Viklund TRITA-SCI-GRU 2020:081 MAT-E 2020:044 Royal Institute of Technology School of Engineering Sciences KTH SCI SE-100 44 Stockholm, Sweden URL: www.kth.se/sci Abstract The implied volatility surface plays an important role for Front office and Risk Manage- ment functions at Nasdaq and other financial institutions which require mark-to-market of derivative books intraday in order to properly value their instruments and measure risk in trading activities. Based on the aforementioned business needs, being able to calibrate an end of day implied volatility surface based on new market information is a sought after trait. In this thesis a statistical learning approach is used to calibrate the implied volatility surface intraday. This is done by using OMXS30-2019 implied volatil- ity surface data in combination with market information from close to at the money options and feeding it into 3 Machine Learning models. The models, including Feed For- ward Neural Network, Recurrent Neural Network and Gaussian Process, were compared based on optimal input and data preprocessing steps. When comparing the best Ma- chine Learning model to the benchmark the performance was similar, indicating that the calibration approach did not offer much improvement. However the calibrated models had a slightly lower spread and average error compared to the benchmark indicating that there is potential of using Machine Learning to calibrate the implied volatility surface. Sammanfattning Implicita volatilitetsytor ¨arett viktigt vektyg f¨orfront office- och riskhanteringsfunk- tioner hos Nasdaq och andra finansiella institut som beh¨over omv¨arderaderas portf¨oljer best˚aendeav derivat under dagen men ocks˚af¨oratt m¨atarisk i handeln. Baserat p˚a ovann¨amndaaff¨arsbehov ¨ardet eftertraktat att kunna kalibrera de implicita volatilitets ytorna som skapas i slutet av dagen n¨astkommande dag baserat p˚any marknadsin- formation. I denna uppsats anv¨andsstatistisk inl¨arningf¨oratt kalibrera dessa ytor. Detta g¨orsgenom att uttnytja historiska ytor fr˚anoptioner i OMXS30 under 2019 i kombination med optioner n¨ara at the money f¨oratt tr¨ana3 Maskininl¨arningsmod- eller. Modellerna inkluderar Feed Forward Neural Network, Recurrent Neural Network och Gaussian Process som vidare j¨amf¨ordesbaserat p˚adata som var bearbetat p˚aolika s¨att. Den b¨astaMaskinl¨arnings modellen j¨amf¨ordesmed ett basv¨ardesom bestod av att anv¨andaf¨oreg˚aendedags yta d¨arresultatet inte innebar n˚agonst¨orref¨orb¨attring. Samtidigt hade modellen en l¨agrespridning samt genomsnittligt fel i j¨amf¨orelsemed basv¨ardetsom indikerar att det finns potential att anv¨anda Maskininl¨arningf¨oratt kalibrera dessa ytor. Acknowledgements We would like to express our gratitude towards our examiner Fredrik Viklund at the De- partment of Mathematics at the Royal Institute of Technology for his feedback regarding our thesis. We would also like to thank our supervisor at Nasdaq, Sebastian Lindberg, for his support, feedback and genuine interest in our project. Also a big thanks to our manager Henrik Hedlund who made sure that we had the data required for this project and David White who introduced us to the subject. Contents List of Figuresi List of Tables iii Acronyms iv 1 Introduction1 1.1 Problem Setting................................2 1.2 Previous Work.................................3 1.3 Thesis Outline.................................3 2 Financial Background4 2.1 Options.....................................4 2.1.1 Put and Call Options.........................4 2.1.2 Option Spreads and Arbitrage....................5 2.1.3 Black Scholes Options Pricing.....................8 2.1.4 Option Risks.............................. 11 2.2 Volatility.................................... 12 2.2.1 Implied Volatility............................ 12 2.2.2 Constructing a Implied Volatility Surface.............. 13 3 Mathematical Background 15 3.1 Statistical Learning Theory.......................... 15 3.1.1 The Loss Function........................... 16 3.1.2 Model Selection: The Bias Variance Dilemma............ 18 3.1.3 Regularisation............................. 19 3.1.4 Dimension Reduction......................... 20 3.2 Artificial Neural Networks........................... 22 3.2.1 Feed Forward Neural Network..................... 22 3.2.2 Recurrent Neural Networks...................... 23 3.2.3 Training a Neural Network...................... 25 3.2.4 Choosing a Network Architecture................... 29 3.2.5 Neural Network Drawbacks...................... 30 3.3 The Gaussian Process............................. 31 3.3.1 Gaussian Process Regression..................... 31 3.3.2 Gaussian Process Model Selection.................. 34 4 Methods 36 4.1 Statistical Learning Approach......................... 36 4.2 The Data.................................... 36 4.2.1 Implied Volatility Data........................ 36 4.2.2 Intraday Data.............................. 38 4.2.3 Feature Engineering.......................... 38 4.2.4 The Final Data Set........................... 39 4.3 Hyperparameter Optimization......................... 39 4.3.1 Optimized Model Parameters..................... 40 4.4 Algorithm Selection.............................. 41 5 Results and Analysis 43 5.1 Data Comparison................................ 43 5.1.1 Feature Engineering.......................... 43 5.1.2 ATM Options.............................. 45 5.2 Model Comparison............................... 46 5.3 Benchmark Comparison............................ 47 6 Discussion and Conclusion 51 6.1 Results Evaluation............................... 51 6.1.1 Data Comparison............................ 51 6.1.2 Model Comparison........................... 52 6.1.3 Benchmark Comparison........................ 52 6.2 Conclusion................................... 52 6.3 Future Work.................................. 53 References 55 Appendicesa A..........................................a A.1 List of OMXS30 listed companies 2019................a A.2 Feature Engineering..........................b List of Figures 2.1 Example of premiums for call and put options with 30 days until expiration.5 2.2 Profit based on stock price for a given vertical spread............6 2.3 Profit based on stock price for a given butterfly spread...........7 2.4 Profit based on stock price for a given calendar spread............8 2.5 Example of a Implied Volatility Surface.................... 13 3.1 Illustration of bias-variance trade-off...................... 19 3.2 Comparison of training and validation error.................. 20 3.3 Single hidden layer Feed Forward Neural Network architecture....... 22 3.4 Example of recurrence in a computational graph............... 24 3.5 Comparison of path of descent for Gradient (red) and Stochastic Gradient Descent (blue), where f(0; 0) minimises the function............. 27 3.6 Computational graph for a single hidden layer Feed Forward Neural Net- work........................................ 28 3.7 Gaussian Processes Regression of the function f(x) = x · sin(x)...... 33 4.1 Comparison of number of unique options observed per trading day using only traded or traded and order data..................... 37 5.1 Comparison of Root Mean Squared Error and Mean Absolute Error be- tween the three different approaches to preprocess the input data..... 44 5.2 Comparison between using three, six or nine closest at the money options in the intraday data per model in terms of Root Mean Squared Error and Mean Absolute Error using Principal Component Analysis data...... 45 5.3 Comparison of Root Mean Squared Error and Mean Absolute Error be- tween the different models for the selected optimal dataset......... 46 5.4 Comparison to see if either model is closer to the previous or future end of day implied volatility surface in terms of Root Mean Squared Error and Mean Absolute Error for optimal data set................... 47 5.5 Comparison of sample Root Mean Squared Error and Mean Absolute Er- ror between the Benchmark and Gaussian Process for the selected optimal dataset...................................... 48 i LIST OF FIGURES 5.6 Comparison of Absolute Error for the implied volatility surface based on time to maturity and log moneyness...................... 49 5.7 3D Comparison of the Root Mean Squared Error for the implied volatility surface based on time to maturity and log moneyness............ 49 5.8 3D Comparison of the Mean Absolute Error for the implied volatility surface based on time to maturity and log moneyness............ 50 A.1 Comparison of Root Mean Squared Error and Mean Absolute Error be- tween the three different approaches to preprocess the input data.....b A.2 Comparison of Root Mean Squared Error and Mean Absolute Error be- tween the three different approaches to preprocess the input data.....b ii List of Tables 4.1 Vol1-Vol5 is the implied volatility at 5 different
Load more

Recommended publications
  • Users/Robertjfrey/Documents/Work
    AMS 511.01 - Foundations Class 11A Robert J. Frey Research Professor Stony Brook University, Applied Mathematics and Statistics [email protected] http://www.ams.sunysb.edu/~frey/ In this lecture we will cover the pricing and use of derivative securities, covering Chapters 10 and 12 in Luenberger’s text. April, 2007 1. The Binomial Option Pricing Model 1.1 – General Single Step Solution The geometric binomial model has many advantages. First, over a reasonable number of steps it represents a surprisingly realistic model of price dynamics. Second, the state price equations at each step can be expressed in a form indpendent of S(t) and those equations are simple enough to solve in closed form. 1+r D-1 u 1 1 + r D 1 + r D y y ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = u fl u = 1+r D u-1 u 1+r-u 1 u 1 u yd yd ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+r D ÅÅÅÅÅÅÅÅ1 uêÅÅÅÅ-ÅÅÅÅu ÅÅ H L H ê L i y As we will see shortlyH weL Hwill solveL the general problemj by solving a zsequence of single step problems on the lattice. That K O K O K O K O j H L H ê L z sequence solutions can be efficientlyê computed because wej only have to zsolve for the state prices once. k { 1.2 – Valuing an Option with One Period to Expiration Let the current value of a stock be S(t) = 105 and let there be a call option with unknown price C(t) on the stock with a strike price of 100 that expires the next three month period.
    [Show full text]
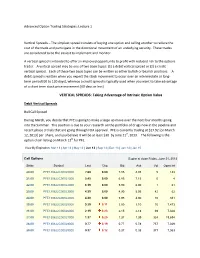
  • VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value
    Advanced Option Trading Strategies: Lecture 1 Vertical Spreads – The simplest spread consists of buying one option and selling another to reduce the cost of the trade and participate in the directional movement of an underlying security. These trades are considered to be the easiest to implement and monitor. A vertical spread is intended to offer an improved opportunity to profit with reduced risk to the options trader. A vertical spread may be one of two basic types: (1) a debit vertical spread or (2) a credit vertical spread. Each of these two basic types can be written as either bullish or bearish positions. A debit spread is written when you expect the stock movement to occur over an intermediate or long- term period [60 to 120 days], whereas a credit spread is typically used when you want to take advantage of a short term stock price movement [60 days or less]. VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value Debit Vertical Spreads Bull Call Spread During March, you decide that PFE is going to make a large up move over the next four months going into the Summer. This position is due to your research on the portfolio of drugs now in the pipeline and recent phase 3 trials that are going through FDA approval. PFE is currently trading at $27.92 [on March 12, 2013] per share, and you believe it will be at least $30 by June 21st, 2013. The following is the option chain listing on March 12th for PFE. View By Expiration: Mar 13 | Apr 13 | May 13 | Jun 13 | Sep 13 | Dec 13 | Jan 14 | Jan 15 Call Options Expire at close Friday,
    [Show full text]
  • A Glossary of Securities and Financial Terms
    A Glossary of Securities and Financial Terms （English to Traditional Chinese） 9-times Restriction Rule 九倍限制規則 24-spread rule 24 個價位規則 1 A AAAC see Academic and Accreditation Advisory Committee【SFC】 ABS see asset-backed securities ACCA see Association of Chartered Certified Accountants, The ACG see Asia-Pacific Central Securities Depository Group ACIHK see ACI-The Financial Markets of Hong Kong ADB see Asian Development Bank ADR see American depositary receipt AFTA see ASEAN Free Trade Area AGM see annual general meeting AIB see Audit Investigation Board AIM see Alternative Investment Market【UK】 AIMR see Association for Investment Management and Research AMCHAM see American Chamber of Commerce AMEX see American Stock Exchange AMS see Automatic Order Matching and Execution System AMS/2 see Automatic Order Matching and Execution System / Second Generation AMS/3 see Automatic Order Matching and Execution System / Third Generation ANNA see Association of National Numbering Agencies AOI see All Ordinaries Index AOSEF see Asian and Oceanian Stock Exchanges Federation APEC see Asia Pacific Economic Cooperation API see Application Programming Interface APRC see Asia Pacific Regional Committee of IOSCO ARM see adjustable rate mortgage ASAC see Asian Securities' Analysts Council ASC see Accounting Society of China 2 ASEAN see Association of South-East Asian Nations ASIC see Australian Securities and Investments Commission AST system see automated screen trading system ASX see Australian Stock Exchange ATI see Account Transfer Instruction ABF Hong
    [Show full text]
  • Volatility As Investment - Crash Protection with Calendar Spreads of Variance Swaps
    Journal of Applied Operational Research (2014) 6(4), 243–254 © Tadbir Operational Research Group Ltd. All rights reserved. www.tadbir.ca ISSN 1735-8523 (Print), ISSN 1927-0089 (Online) Volatility as investment - crash protection with calendar spreads of variance swaps Uwe Wystup 1,* and Qixiang Zhou 2 1 MathFinance AG, Frankfurt, Germany 2 Frankfurt School of Finance & Management, Germany Abstract. Nowadays, volatility is not only a risk measure but can be also considered an individual asset class. Variance swaps, one of the main investment vehicles, can obtain pure exposure on realized volatility. In normal market phases, implied volatility is often higher than the realized volatility will turn out to be. We present a volatility investment strategy that can benefit from both negative risk premium and correlation of variance swaps to the underlying stock index. The empirical evidence demonstrates a significant diversification effect during the financial crisis by adding this strategy to an existing portfolio consisting of 70% stocks and 30% bonds. The back-testing analysis includes the last ten years of history of the S&P500 and the EUROSTOXX50. Keywords: volatility; investment strategy; stock index; crash protection; variance swap * Received July 2014. Accepted November 2014 Introduction Volatility is an important variable of the financial market. The accurate measurement of volatility is important not only for investment but also as an integral part of risk management. Generally, there are two methods used to assess volatility: The first one entails the application of time series methods in order to make statistical conclusions based on historical data. Examples of this method are ARCH/GARCH models.
    [Show full text]
  • Spread Scanner Guide Spread Scanner Guide
    Spread Scanner Guide Spread Scanner Guide ..................................................................................................................1 Introduction ...................................................................................................................................2 Structure of this document ...........................................................................................................2 The strategies coverage .................................................................................................................2 Spread Scanner interface..............................................................................................................3 Using the Spread Scanner............................................................................................................3 Profile pane..................................................................................................................................3 Position Selection pane................................................................................................................5 Stock Selection pane....................................................................................................................5 Position Criteria pane ..................................................................................................................7 Additional Parameters pane.........................................................................................................7 Results section .............................................................................................................................8
    [Show full text]
  • The Impact of Implied Volatility Fluctuations on Vertical Spread Option Strategies: the Case of WTI Crude Oil Market
    energies Article The Impact of Implied Volatility Fluctuations on Vertical Spread Option Strategies: The Case of WTI Crude Oil Market Bartosz Łamasz * and Natalia Iwaszczuk Faculty of Management, AGH University of Science and Technology, 30-059 Cracow, Poland; [email protected] * Correspondence: [email protected]; Tel.: +48-696-668-417 Received: 31 July 2020; Accepted: 7 October 2020; Published: 13 October 2020 Abstract: This paper aims to analyze the impact of implied volatility on the costs, break-even points (BEPs), and the final results of the vertical spread option strategies (vertical spreads). We considered two main groups of vertical spreads: with limited and unlimited profits. The strategy with limited profits was divided into net credit spread and net debit spread. The analysis takes into account West Texas Intermediate (WTI) crude oil options listed on New York Mercantile Exchange (NYMEX) from 17 November 2008 to 15 April 2020. Our findings suggest that the unlimited vertical spreads were executed with profits less frequently than the limited vertical spreads in each of the considered categories of implied volatility. Nonetheless, the advantage of unlimited strategies was observed for substantial oil price movements (above 10%) when the rates of return on these strategies were higher than for limited strategies. With small price movements (lower than 5%), the net credit spread strategies were by far the best choice and generated profits in the widest price ranges in each category of implied volatility. This study bridges the gap between option strategies trading, implied volatility and WTI crude oil market. The obtained results may be a source of information in hedging against oil price fluctuations.
    [Show full text]
  • Copyrighted Material
    Index AA estimate, 68–69 At-the-money (ATM) SPX variance Affine jump diffusion (AJD), 15–16 levels/skews, 39f AJD. See Affine jump diffusion Avellaneda, Marco, 114, 163 Alfonsi, Aurelien,´ 163 American Airlines (AMR), negative book Bakshi, Gurdip, 66, 163 value, 84 Bakshi-Cao-Chen (BCC) parameters, 40, 66, American implied volatilities, 82 67f, 70f, 146, 152, 154f American options, 82 Barrier level, Amortizing options, 135 distribution, 86 Andersen, Leif, 24, 67, 68, 163 equal to strike, 108–109 Andreasen, Jesper, 67, 68, 163 Barrier options, 107, 114. See also Annualized Heston convexity adjustment, Out-of-the-money barrier options 145f applications, 120 Annualized Heston VXB convexity barrier window, 120 adjustment, 160f definitions, 107–108 Ansatz, 32–33 discrete monitoring, adjustment, 117–119 application, 34 knock-in options, 107 Arbitrage, 78–79. See also Capital structure knock-out options, 107, 108 arbitrage limiting cases, 108–109 avoidance, 26 live-out options, 116, 117f calendar spread arbitrage, 26 one-touch options, 110, 111f, 112f, 115 vertical spread arbitrage, 26, 78 out-of-the-money barrier, 114–115 Arrow-Debreu prices, 8–9 Parisian options, 120 Asymptotics, summary, 100 rebate, 108 Benaim, Shalom, 98, 163 At-the-money (ATM) implied volatility (or Berestycki, Henri, 26, 163 variance), 34, 37, 39, 79, 104 Bessel functions, 23, 151. See also Modified structure, computation, 60 Bessel function At-the-money (ATM) lookback (hindsight) weights, 149 option, 119 Bid/offer spread, 26 At-the-money (ATM) option, 70, 78, 126, minimization,
    [Show full text]
  • Smile Arbitrage: Analysis and Valuing
    UNIVERSITY OF ST. GALLEN Master program in banking and finance MBF SMILE ARBITRAGE: ANALYSIS AND VALUING Master’s Thesis Author: Alaa El Din Hammam Supervisor: Prof. Dr. Karl Frauendorfer Dietikon, 15th May 2009 Author: Alaa El Din Hammam Title of thesis: SMILE ARBITRAGE: ANALYSIS AND VALUING Date: 15th May 2009 Supervisor: Prof. Dr. Karl Frauendorfer Abstract The thesis studies the implied volatility, how it is recognized, modeled, and the ways used by practitioners in order to benefit from an arbitrage opportunity when compared to the realized volatility. Prediction power of implied volatility is exam- ined and findings of previous studies are supported, that it has the best prediction power of all existing volatility models. When regressed on implied volatility, real- ized volatility shows a high beta of 0.88, which contradicts previous studies that found lower betas. Moment swaps are discussed and the ways to use them in the context of volatility trading, the payoff of variance swaps shows a significant neg- ative variance premium which supports previous findings. An algorithm to find a fair value of a structured product aiming to profit from skew arbitrage is presented and the trade is found to be profitable in some circumstances. Different suggestions to implement moment swaps in the context of portfolio optimization are discussed. Keywords: Implied volatility, realized volatility, moment swaps, variance swaps, dispersion trading, skew trading, derivatives, volatility models Language: English Contents Abbreviations and Acronyms i 1 Introduction 1 1.1 Initial situation . 1 1.2 Motivation and goals of the thesis . 2 1.3 Structure of the thesis . 3 2 Volatility 5 2.1 Volatility in the Black-Scholes world .
    [Show full text]
  • Fidelity 2017 Credit Spreads
    Credit Spreads – And How to Use Them Marty Kearney 789768.1.0 1 Disclaimer Options involve risks and are not suitable for everyone. Individuals should not enter into options transactions until they have read and understood the risk disclosure document, Characteristics and Risks of Standardized Options, available by visiting OptionsEducation.org. To obtain a copy, contact your broker or The Options Industry Council at One North Wacker Drive, Chicago, IL 60606. Individuals should not enter into options transactions until they have read and understood this document. In order to simplify the computations used in the examples in these materials, commissions, fees, margin interest and taxes have not been included. These costs will impact the outcome of any stock and options transactions and must be considered prior to entering into any transactions. Investors should consult their tax advisor about any potential tax consequences. Any strategies discussed, including examples using actual securities and price data, are strictly for illustrative and educational purposes and should not be construed as an endorsement, recommendation, or solicitation to buy or sell securities. Past performance is not a guarantee of future results. 2 Spreads . What is an Option Spread? . An Example of a Vertical Debit Spread . Examples of Vertical Credit Spreads . How to choose strike prices when employing the Vertical Credit Spread strategy . Note: Any mention of Credit Spread today is using a Vertical Credit Spread. 3 A Spread A Spread is a combination trade, buying and/or selling two or more financial products. It could be stock and stock (long Coca Cola – short shares of Pepsi), Stock and Option (long Qualcomm, short a March QCOM call - many investors have used the “Covered Call”), maybe long an IBM call and Put.
    [Show full text]
  • Arbitrage Spread.Pdf
    Arbitrage spreads Arbitrage spreads refer to standard option strategies like vanilla spreads to lock up some arbitrage in case of mispricing of options. Although arbitrage used to exist in the early days of exchange option markets, these cheap opportunities have almost completely disappeared, as markets have become more and more efficient. Nowadays, millions of eyes as well as computer software are hunting market quote screens to find cheap bargain, reducing the life of a mispriced quote to a few seconds. In addition, standard option strategies are now well known by the various market participants. Let us review the various standard arbitrage spread strategies Like any trades, spread strategies can be decomposed into bullish and bearish ones. Bullish position makes money when the market rallies while bearish does when the market sells off. The spread option strategies can decomposed in the following two categories: Spreads: Spread trades are strategies that involve a position on two or more options of the same type: either a call or a put but never a combination of the two. Typical spreads are bull, bear, calendar, vertical, horizontal, diagonal, butterfly, condors. Combination: in contrast to spreads combination trade implies to take a position on both call and puts. Typical combinations are straddle, strangle1, and risk reversal. Spreads (bull, bear, calendar, vertical, horizontal, diagonal, butterfly, condors) Spread trades are a way of taking views on the difference between two or more assets. Because the trading strategy plays on the relative difference between different derivatives, the risk and the upside are limited. There are many types of spreads among which bull, bear, and calendar, vertical, horizontal, diagonal, butterfly spreads are the most famous.
    [Show full text]
  • The Option Trader Handbook Strategies and Trade Adjustments
    The Option Trader Handbook Strategies and Trade Adjustments Second Edition GEORGE VI. JABBOIiR, PhD PHILIP H. BUDWICK, MsF WILEY John Wiley & Sons, Inc. Contents Preface to the First Edition xlli Preface to the Second Edition xvli CHAPTER 1 Trade and Risk Management 1 Introduction 1 The Philosophy of Risk 2 Truth About Reward 5 Risk Management 6 Risk 6 Reward 9 Breakeven Points , 11 Trade Management 11 Trading Theme 11 The Theme of Your Portfolio 14 Diversification and Flexibility 15 Trading as a Business 16 Start-Up Phase 16 Growth Phase 19 Mature Phase 20 Just Business, Nothing Personal 21 SCORE—The Formula for Trading Success 21 Select the Investment 22 Choose the Best Strategy 23 Open the Trade with a Plan v, 24 Remember Your Plan and Stick to It 26 Exit Your Trade 26 Vl CONTENTS CHAPTER 2 Tools of the Trader 29 Introduction 29 Option Value 30 Option Pricing 31 Stock Price 31 Strike Price 32 Time to Expiration 32 Volatility 33 Dividends 33 Interest Rates 33 Option Greeks and Risk Management 34 Time Decay 34 Trading Lessons Learned from Time Decay (Theta). 41 Delta/Gamma 43 Deep-in-the-Money Options 46 Implied Volatility 49 Early Assignment 63 Synthetic Positions 65 Synthetic Stock 66 Long Stock 66 Short Stock 67 Synthetic Call 68 Synthetic Put 70 Basic Strategies 71 Long Call , 71 Short Call . - 72 Long Put .' 73 Short Put 74 Basic Spreads and Combinations 75 Bull Call Spread 75 Bull Put Spread 76 Bear Call Spread 77 Bear Put Spread 78 Long Straddle 78 Long Strangle 79 Short Straddle 80 Short Strangle 81 Advanced Spreads 82 Call Ratio
    [Show full text]
  • Causes of Market Anomalies of Crude Oil Calendar Spreads: Does Theory of Storage Address the Issue?”
    “Causes of market anomalies of crude oil calendar spreads: does theory of storage address the issue?” AUTHORS Kirill Perchanok Nada K. Kakabadse Kirill Perchanok and Nada K. Kakabadse (2013). Causes of market anomalies of ARTICLE INFO crude oil calendar spreads: does theory of storage address the issue?. Problems and Perspectives in Management, 11(2) RELEASED ON Monday, 01 July 2013 JOURNAL "Problems and Perspectives in Management" FOUNDER LLC “Consulting Publishing Company “Business Perspectives” NUMBER OF REFERENCES NUMBER OF FIGURES NUMBER OF TABLES 0 0 0 © The author(s) 2021. This publication is an open access article. businessperspectives.org Problems and Perspectives in Management, Volume 11, Issue 2, 2013 SECTION 2. Management in firms and organizations Kirill Perchanok (UK), Nada K. Kakabadse (UK) Causes of market anomalies of crude oil calendar spreads: does theory of storage address the issue? Abstract Beginning with the 2008 financial crisis, crude oil futures market participants began to observe situations where contango spread values exceeded carrying charge amounts many times over and lasted relatively long. The article describes these unusual occurrences on the example of the behavior of crude oil calendar spreads and analyzes the causes for such anomalies. Moreover, most researchers have focused on studying the market in a state of normal backwardation, paying much less attention to the market in contango. The recent appearance of “wild” contangos of anomalous dimensions in the futures markets shows that the theory of storage and the cost of carry model requires revision in order to align the model’s theoretical foundation with the empirical observations. This article’s main aim is the desire to draw attention to the need for updating the theory of storage and the cost of carry model.
    [Show full text]