DOCSLIB.ORG

Users/Robertjfrey/Documents/Work

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Users/Robertjfrey/Documents/Work AMS 511.01 - Foundations Class 11A Robert J. Frey Research Professor Stony Brook University, Applied Mathematics and Statistics [email protected] http://www.ams.sunysb.edu/~frey/ In this lecture we will cover the pricing and use of derivative securities, covering Chapters 10 and 12 in Luenberger’s text. April, 2007 1. The Binomial Option Pricing Model 1.1 – General Single Step Solution The geometric binomial model has many advantages. First, over a reasonable number of steps it represents a surprisingly realistic model of price dynamics. Second, the state price equations at each step can be expressed in a form indpendent of S(t) and those equations are simple enough to solve in closed form. 1+r D-1 u 1 1 + r D 1 + r D y y ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = u fl u = 1+r D u-1 u 1+r-u 1 u 1 u yd yd ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+r D ÅÅÅÅÅÅÅÅ1 uêÅÅÅÅ-ÅÅÅÅu ÅÅ H L H ê L i y As we will see shortlyH weL Hwill solveL the general problemj by solving a zsequence of single step problems on the lattice. That K O K O K O K O j H L H ê L z sequence solutions can be efficientlyê computed because wej only have to zsolve for the state prices once. k { 1.2 – Valuing an Option with One Period to Expiration Let the current value of a stock be S(t) = 105 and let there be a call option with unknown price C(t) on the stock with a strike price of 100 that expires the next three month period. We’ll use a single binomial step, so D = 0.25 months. For the period of t to t+D the risky return is u = 110%; the binomial probability is Pu = 0.50, and the annual risk free rate is r = 0.04. 1 1 + r D 1 + r D 1 1.01 1.01 y y S t = u S t S t u u fl 105 = 115.50 95.45 u y y C t max u S t - K, 0 max S t u - K, 0 d C t 15.5 0 d H L H L ji zy ji zy ji zy ji zy j z j z j z j z We can solvej H L thez firstj two equationsH L for the stateH pricesL ê usingz Kthe closedO formj solutionz j z K O j z j z j z j z k H L { k 1+r D-@ 1 u H L D 1+0.04µ@0.25H L-ê1 1.10 D { k H L { y ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 0.523 k { u = 1+r D u-1 u = 1+0.04µ0.25 1.10-1 1.10 = 1+r D-u 1+0.04µ0.25-1.10 yd 0.467 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+r D ÅÅÅÅÅÅÅÅ1 uêÅÅÅÅ-ÅÅÅÅu ÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+0.04µ0.25 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1 1.10ê -ÅÅÅÅÅÅÅÅ1.10ÅÅÅÅÅ H L H ê L H L H ê L i y i y If we take these valuesj and substitutez j them into the last rowz we realize a call premium of C(t) > 5.23. K O j H L H ê L z j H L H ê L z K O j è z j z The risk neutral kmeasure P is { k { 2 ams-511-lec-11A-p.nb è Pu 1 yu 1 0.673 0.529 è = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = Pd 1 + r D yd 1 + 0.01 0.288 0.471 It is remarkablei y but, other than meeting the requirement that 0 < P < 1, the ordinary probability measure does not play a role j z u in the solution.j z K O K O K O k { 1.3 – The General Binomial Option Pricing Model We’ll return to the example above but now assume that the option expires is six months, but we wish to model the stock price evolution using two lattice steps. The binomial lattice for the stock is then 127.05 115.50 105.00 105.00 95.45 86.78 As before, the risk neutral measure is è Pu 0.529 è = Pd 0.471 The “leaves”i y of the lattice above occur at expiry, so for each price node we can calculate the value of the call option. This j z gives us jthe z K O k { 27.05 5.00 0.00 è T T 1 Pu 27.05 1 0.529 27.05 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ è = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = 16.49 1 + r D Pd 5.00 1.01 0.471 5.00 i è yT T 1 j Pu z 5.00 1 0.529 5.00 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ j è z K O= ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ K O K =O 2.62 1 + r D k Pd { 0.00 1.01 0.471 0.00 i y j z j z K O K O K O k { ams-511-lec-11A-p.nb 3 We can now add this information to the lattice. 27.05 16.49 5.00 2.62 0.00 è T T 1 Pu 16.49 1 0.529 16.49 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ è = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = 9.85 1 + r D Pd 2.62 1.01 0.471 2.62 This allows us toi completey the lattice. The value at the “root”, 9.85, is the value of the call option. j z j z K O K O K O k { 27.05 16.49 9.85 5.00 2.62 0.00 1.4 – Calibrating the Model to Market Data For a given stepsize D we have two free parameters in the geometric binomial model: Pu and u. As was shown earlier, with a sufficient number of steps the log price tends towards a Normal distribution. The calibration of the geometric binomial model at stepsize D, therefore, involves selecting a set of parameters Pu and u so that the mean and standard deviation of the log price are matched. S t + 1 m = E log ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ S t + 2 H S t L 1 s = VarC Clog ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅGGÅÅÅÅÅÅÅÅ H LS t 1 m H L Pu = ÅÅÅÅÅ 1C + CÅÅÅÅÅÅÅ D GG 2 s H L s D u = e è!!!! J N è!!!! 4 ams-511-lec-11A-p.nb 1.5 – Mathematica Code This code is not the most efficient; it’s meant to illustrate the computations in the simplest terms. Each step or level in the lattice is represented by a list. The entire lattice is a list of such lists, e.g., {{x11},. {x21, x22}, {x31, x32, x33}, ...}. The function fLatticeForwardStep takes one level of the lattice and produces the successor level using the supplied nUpFactor. fLatticeForwardStep vnOneLevel_, nUpFactor_ := Append vnOneLevel nUpFactor, Last vnOneLevel nUpFactor ; è The function fRiskNeutralMeasure calculates the value of Pu assuming a geometric binomial model. @ D fRiskNeutralMeasure nRiskFree_, DTime_, nUpFactor_ := @ @ D ê D -1 + nUpFactor + nRiskFree nUpFactor DTime ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ; -1 + nUpFactor2 @ D These functions are used at the leaves of the undelying’s lattice to compute the leaves of the option’s lattice. fCallAtExpiry nNowPrice_, nStrikePrice_ := Max nNowPrice - nStrikePrice, 0 ; fPutAtExpiry nNowPrice_, nStrikePrice_ := Max nStrikePrice@ - nNowPrice, 0 ; D @ D fLatticeBackStep vnOneLevel_, nRiskFree_,@ DTime_, nRiskNeutralProb_D := Module i@, D Table @ nRiskNeutralProb vnOneLevel i + 1D- nRiskNeutralProb@ 8 < vnOneLevel i + 1 1 + nRiskFree DTime , i, 1@, Length vnOneLevel - 1 H P T H L ; P TL ê H L 8 @ D < D D ams-511-lec-11A-p.nb 5 This is the top-level function. It returns the risk neutral measure, the underlying’s “forward” lattice, and the option’s “backward” lattice. Note that the forward and backward lattices, whose variables I’ve somewhat incorrectly called trees in the code, are computed by using NestList to recursively apply fLatticeForwardStep from the root to the leaves and then fLatticeBackStep from the leaves to the root. The last parameter is a character with “c” for a call and “p” for a put. fGeometricBinomialOption nNowPrice_, nUpFactor_, nStrikePrice_, nRiskFree_, iIntervals_, DTime_, cPutCall_ := Module vvnBackwardTree, @ vnExpiryPrice, vvnForwardTree, nRiskNeutralProb , vvnForwardTree = NestListD @ 8 fLatticeForwardStep #, nUpFactor &, nNowPrice , < iIntervals @ ; @ D nRiskNeutralProb8 < = fRiskNeutralMeasure nRiskFree, DTime, nUpFactor ; vnExpiryPriceD = If cPutCall == c, fCallAtExpiry #, nStrikePrice & ü Last vvnForwardTree , fPutAtExpiry #, nStrikePrice@ & ü Last vvnForwardTreeD ; @ vvnBackwardTree@= NestList D ê @ D fLatticeBackStep@ #, nRiskFreeD, DêTime, nRiskNeutralProb@ D &, DvnExpiryPrice, iIntervals @ ; @ D nRiskNeutralProb, vvnForwardTree, vvnBackwardTree ; D 8 < D 6 ams-511-lec-11A-p.nb 1.6 – Example: Pricing a Put Option Consider a stock with current price S(0)=125. It’s log mean and variance are m = 0.10 and s2=0.01. There is a put option on the stock with expiry T=0.5 and a strike price K = 120. The annual risk free rate is 4%. Estimate the price of the put option using a 5-step geometric binomial option model. nTimeToExpiry = 0.5; iIntervals = 10; DTime = nTimeToExpiry iIntervals; nUpFactor = Exp 0.01 DTime ; ê nRiskNeutral, vvnStockLatticeè!!!!!!!!!!!!!!!!!!!!!!!!! , vvnOptionLattice = fGeometricBinomialOptionB F125, nUpFactor, 120, 0.04, iIntervals, DTime, p ; 8 < MatrixForm ü vvnStockLattice@ MatrixForm ü vvnOptionLattice D ê ê ams-511-lec-11A-p.nb 7 ol o 136.696 o 133.673 o 130.717 130.717 o o 127.827 127.827 o 125 , , 125. , , 125. , o 122.236 122.236 o i y o 119.533 j 119.533 z o ji 116.89 zy j z o ji zy j z j 114.305 z o j z j z j z mH L K O j z j z j z o j z j z j z o j z j z j z o k { j z j z o k { j z o o k { o o o o o o n 156.322 149.485 152.866 149.485 146.18 142.948 142.948 146.18 142.948 139.787 139.787 139.787 136.696 136.696 ji 136.696 zyo| j zo 133.673 133.673 ji 133.673 zy j zo 130.717 ji 130.717 zy j z j 130.717 zo 127.827 i 127.827 y j z j z j zo i 125.
Load more

Recommended publications
  • Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces
    DEGREE PROJECT IN MATHEMATICS, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2020 Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ENGINEERING SCIENCES Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON Degree Projects in Mathematical Statistics (30 ECTS credits) Master's Programme in Applied and Computational Mathematics (120 credits) KTH Royal Institute of Technology year 2020 Supervisor at Nasdaq Technology AB: Sebastian Lindberg Supervisor at KTH: Fredrik Viklund Examiner at KTH: Fredrik Viklund TRITA-SCI-GRU 2020:081 MAT-E 2020:044 Royal Institute of Technology School of Engineering Sciences KTH SCI SE-100 44 Stockholm, Sweden URL: www.kth.se/sci Abstract The implied volatility surface plays an important role for Front office and Risk Manage- ment functions at Nasdaq and other financial institutions which require mark-to-market of derivative books intraday in order to properly value their instruments and measure risk in trading activities. Based on the aforementioned business needs, being able to calibrate an end of day implied volatility surface based on new market information is a sought after trait. In this thesis a statistical learning approach is used to calibrate the implied volatility surface intraday. This is done by using OMXS30-2019 implied volatil- ity surface data in combination with market information from close to at the money options and feeding it into 3 Machine Learning models. The models, including Feed For- ward Neural Network, Recurrent Neural Network and Gaussian Process, were compared based on optimal input and data preprocessing steps.
    [Show full text]
  • Shadow Banking
    Federal Reserve Bank of New York Staff Reports Shadow Banking Zoltan Pozsar Tobias Adrian Adam Ashcraft Hayley Boesky Staff Report No. 458 July 2010 Revised February 2012 FRBNY Staff REPORTS This paper presents preliminary findings and is being distributed to economists and other interested readers solely to stimulate discussion and elicit comments. The views expressed in this paper are those of the authors and are not necessar- ily reflective of views at the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the authors. Shadow Banking Zoltan Pozsar, Tobias Adrian, Adam Ashcraft, and Hayley Boesky Federal Reserve Bank of New York Staff Reports, no. 458 July 2010: revised February 2012 JEL classification: G20, G28, G01 Abstract The rapid growth of the market-based financial system since the mid-1980s changed the nature of financial intermediation. Within the market-based financial system, “shadow banks” have served a critical role. Shadow banks are financial intermediaries that con- duct maturity, credit, and liquidity transformation without explicit access to central bank liquidity or public sector credit guarantees. Examples of shadow banks include finance companies, asset-backed commercial paper (ABCP) conduits, structured investment vehicles (SIVs), credit hedge funds, money market mutual funds, securities lenders, limited-purpose finance companies (LPFCs), and the government-sponsored enterprises (GSEs). Our paper documents the institutional features of shadow banks, discusses their economic roles, and analyzes their relation to the traditional banking system. Our de- scription and taxonomy of shadow bank entities and shadow bank activities are accom- panied by “shadow banking maps” that schematically represent the funding flows of the shadow banking system.
    [Show full text]
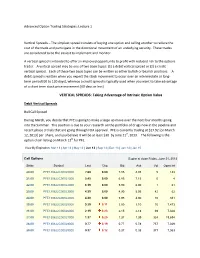
  • VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value
    Advanced Option Trading Strategies: Lecture 1 Vertical Spreads – The simplest spread consists of buying one option and selling another to reduce the cost of the trade and participate in the directional movement of an underlying security. These trades are considered to be the easiest to implement and monitor. A vertical spread is intended to offer an improved opportunity to profit with reduced risk to the options trader. A vertical spread may be one of two basic types: (1) a debit vertical spread or (2) a credit vertical spread. Each of these two basic types can be written as either bullish or bearish positions. A debit spread is written when you expect the stock movement to occur over an intermediate or long- term period [60 to 120 days], whereas a credit spread is typically used when you want to take advantage of a short term stock price movement [60 days or less]. VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value Debit Vertical Spreads Bull Call Spread During March, you decide that PFE is going to make a large up move over the next four months going into the Summer. This position is due to your research on the portfolio of drugs now in the pipeline and recent phase 3 trials that are going through FDA approval. PFE is currently trading at $27.92 [on March 12, 2013] per share, and you believe it will be at least $30 by June 21st, 2013. The following is the option chain listing on March 12th for PFE. View By Expiration: Mar 13 | Apr 13 | May 13 | Jun 13 | Sep 13 | Dec 13 | Jan 14 | Jan 15 Call Options Expire at close Friday,
    [Show full text]
  • A Glossary of Securities and Financial Terms
    A Glossary of Securities and Financial Terms （English to Traditional Chinese） 9-times Restriction Rule 九倍限制規則 24-spread rule 24 個價位規則 1 A AAAC see Academic and Accreditation Advisory Committee【SFC】 ABS see asset-backed securities ACCA see Association of Chartered Certified Accountants, The ACG see Asia-Pacific Central Securities Depository Group ACIHK see ACI-The Financial Markets of Hong Kong ADB see Asian Development Bank ADR see American depositary receipt AFTA see ASEAN Free Trade Area AGM see annual general meeting AIB see Audit Investigation Board AIM see Alternative Investment Market【UK】 AIMR see Association for Investment Management and Research AMCHAM see American Chamber of Commerce AMEX see American Stock Exchange AMS see Automatic Order Matching and Execution System AMS/2 see Automatic Order Matching and Execution System / Second Generation AMS/3 see Automatic Order Matching and Execution System / Third Generation ANNA see Association of National Numbering Agencies AOI see All Ordinaries Index AOSEF see Asian and Oceanian Stock Exchanges Federation APEC see Asia Pacific Economic Cooperation API see Application Programming Interface APRC see Asia Pacific Regional Committee of IOSCO ARM see adjustable rate mortgage ASAC see Asian Securities' Analysts Council ASC see Accounting Society of China 2 ASEAN see Association of South-East Asian Nations ASIC see Australian Securities and Investments Commission AST system see automated screen trading system ASX see Australian Stock Exchange ATI see Account Transfer Instruction ABF Hong
    [Show full text]
  • Credit Derivatives in Managing Off Balance Sheet Risks by Banks
    City University Business School MSc in Finance 2001 Credit Derivatives in Managing Off Balance Sheet Risks by Banks Submitted by Murat Cakir Supervisor: Giorgio S. Questa This project is submitted as part of the requirements for the award of the MSc in Finance. July 2001 ABSTRACT Credit risk has been a worrying type of risk for financial managers. Fortunately, a recent market development –credit derivatives- has made the credit risk more manageable. The loan portfolio management has become more practicable than it used to be in the past. However, credit derivatives are still not well examined. There are uncertainties about and difficulties in the pricing and portfolio management of credit derivatives due to the non-normality in probability distribution of credit risk. Various models have been developed for credit derivatives pricing. After having drawn the general picture for the credit derivatives, we have studied some recent pricing models in a Das (1999) framework, in this study. Also appended is a an attempt to a step forward for simulating the risk-free rates and spreads, to test how powerful simulation can be in modeling the credit risk and pricing of it. Moreover, with highly developed computer technology, it is possible to make sensitivity analysis under several scenarios, to form imaginary loan portfolios, find their risk exposures, and perform a successful risk management practice. COPYRIGHT MURAT ÇAKIR Central Bank of the Republic of Turkey. All rights reserved. No part of this work 2 may be reproduced, stored in a retrieval system, transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except formal use of reference to the author without the written permission thereof Acknowledgements I am deeply grateful to my supervisor Mr.
    [Show full text]
  • The Impact of Implied Volatility Fluctuations on Vertical Spread Option Strategies: the Case of WTI Crude Oil Market
    energies Article The Impact of Implied Volatility Fluctuations on Vertical Spread Option Strategies: The Case of WTI Crude Oil Market Bartosz Łamasz * and Natalia Iwaszczuk Faculty of Management, AGH University of Science and Technology, 30-059 Cracow, Poland; [email protected] * Correspondence: [email protected]; Tel.: +48-696-668-417 Received: 31 July 2020; Accepted: 7 October 2020; Published: 13 October 2020 Abstract: This paper aims to analyze the impact of implied volatility on the costs, break-even points (BEPs), and the final results of the vertical spread option strategies (vertical spreads). We considered two main groups of vertical spreads: with limited and unlimited profits. The strategy with limited profits was divided into net credit spread and net debit spread. The analysis takes into account West Texas Intermediate (WTI) crude oil options listed on New York Mercantile Exchange (NYMEX) from 17 November 2008 to 15 April 2020. Our findings suggest that the unlimited vertical spreads were executed with profits less frequently than the limited vertical spreads in each of the considered categories of implied volatility. Nonetheless, the advantage of unlimited strategies was observed for substantial oil price movements (above 10%) when the rates of return on these strategies were higher than for limited strategies. With small price movements (lower than 5%), the net credit spread strategies were by far the best choice and generated profits in the widest price ranges in each category of implied volatility. This study bridges the gap between option strategies trading, implied volatility and WTI crude oil market. The obtained results may be a source of information in hedging against oil price fluctuations.
    [Show full text]
  • Copyrighted Material
    Index AA estimate, 68–69 At-the-money (ATM) SPX variance Affine jump diffusion (AJD), 15–16 levels/skews, 39f AJD. See Affine jump diffusion Avellaneda, Marco, 114, 163 Alfonsi, Aurelien,´ 163 American Airlines (AMR), negative book Bakshi, Gurdip, 66, 163 value, 84 Bakshi-Cao-Chen (BCC) parameters, 40, 66, American implied volatilities, 82 67f, 70f, 146, 152, 154f American options, 82 Barrier level, Amortizing options, 135 distribution, 86 Andersen, Leif, 24, 67, 68, 163 equal to strike, 108–109 Andreasen, Jesper, 67, 68, 163 Barrier options, 107, 114. See also Annualized Heston convexity adjustment, Out-of-the-money barrier options 145f applications, 120 Annualized Heston VXB convexity barrier window, 120 adjustment, 160f definitions, 107–108 Ansatz, 32–33 discrete monitoring, adjustment, 117–119 application, 34 knock-in options, 107 Arbitrage, 78–79. See also Capital structure knock-out options, 107, 108 arbitrage limiting cases, 108–109 avoidance, 26 live-out options, 116, 117f calendar spread arbitrage, 26 one-touch options, 110, 111f, 112f, 115 vertical spread arbitrage, 26, 78 out-of-the-money barrier, 114–115 Arrow-Debreu prices, 8–9 Parisian options, 120 Asymptotics, summary, 100 rebate, 108 Benaim, Shalom, 98, 163 At-the-money (ATM) implied volatility (or Berestycki, Henri, 26, 163 variance), 34, 37, 39, 79, 104 Bessel functions, 23, 151. See also Modified structure, computation, 60 Bessel function At-the-money (ATM) lookback (hindsight) weights, 149 option, 119 Bid/offer spread, 26 At-the-money (ATM) option, 70, 78, 126, minimization,
    [Show full text]
  • Put/Call Parity
    Execution * Research 141 W. Jackson Blvd. 1220A Chicago, IL 60604 Consulting * Asset Management The grain markets had an extremely volatile day today, and with the wheat market locked limit, many traders and customers have questions on how to figure out the futures price of the underlying commodities via the options market - Or the synthetic value of the futures. Below is an educational piece that should help brokers, traders, and customers find that synthetic value using the options markets. Any questions please do not hesitate to call us. Best Regards, Linn Group Management PUT/CALL PARITY Despite what sometimes seems like utter chaos and mayhem, options markets are in fact, orderly and uniform. There are some basic and easy to understand concepts that are essential to understanding the marketplace. The first and most important option concept is called put/call parity . This is simply the relationship between the underlying contract and the same strike, put and call. The formula is: Call price – put price + strike price = future price* Therefore, if one knows any two of the inputs, the third can be calculated. This triangular relationship is the cornerstone of understanding how options work and is true across the whole range of out of the money and in the money strikes. * To simplify the formula we have assumed no dividends, no early exercise, interest rate factors or liquidity issues. By then using this concept of put/call parity one can take the next step and create synthetic positions using options. For example, one could buy a put and sell a call with the same exercise price and expiration date which would be the synthetic equivalent of a short future position.
    [Show full text]
  • Smile Arbitrage: Analysis and Valuing
    UNIVERSITY OF ST. GALLEN Master program in banking and finance MBF SMILE ARBITRAGE: ANALYSIS AND VALUING Master’s Thesis Author: Alaa El Din Hammam Supervisor: Prof. Dr. Karl Frauendorfer Dietikon, 15th May 2009 Author: Alaa El Din Hammam Title of thesis: SMILE ARBITRAGE: ANALYSIS AND VALUING Date: 15th May 2009 Supervisor: Prof. Dr. Karl Frauendorfer Abstract The thesis studies the implied volatility, how it is recognized, modeled, and the ways used by practitioners in order to benefit from an arbitrage opportunity when compared to the realized volatility. Prediction power of implied volatility is exam- ined and findings of previous studies are supported, that it has the best prediction power of all existing volatility models. When regressed on implied volatility, real- ized volatility shows a high beta of 0.88, which contradicts previous studies that found lower betas. Moment swaps are discussed and the ways to use them in the context of volatility trading, the payoff of variance swaps shows a significant neg- ative variance premium which supports previous findings. An algorithm to find a fair value of a structured product aiming to profit from skew arbitrage is presented and the trade is found to be profitable in some circumstances. Different suggestions to implement moment swaps in the context of portfolio optimization are discussed. Keywords: Implied volatility, realized volatility, moment swaps, variance swaps, dispersion trading, skew trading, derivatives, volatility models Language: English Contents Abbreviations and Acronyms i 1 Introduction 1 1.1 Initial situation . 1 1.2 Motivation and goals of the thesis . 2 1.3 Structure of the thesis . 3 2 Volatility 5 2.1 Volatility in the Black-Scholes world .
    [Show full text]
  • Fidelity 2017 Credit Spreads
    Credit Spreads – And How to Use Them Marty Kearney 789768.1.0 1 Disclaimer Options involve risks and are not suitable for everyone. Individuals should not enter into options transactions until they have read and understood the risk disclosure document, Characteristics and Risks of Standardized Options, available by visiting OptionsEducation.org. To obtain a copy, contact your broker or The Options Industry Council at One North Wacker Drive, Chicago, IL 60606. Individuals should not enter into options transactions until they have read and understood this document. In order to simplify the computations used in the examples in these materials, commissions, fees, margin interest and taxes have not been included. These costs will impact the outcome of any stock and options transactions and must be considered prior to entering into any transactions. Investors should consult their tax advisor about any potential tax consequences. Any strategies discussed, including examples using actual securities and price data, are strictly for illustrative and educational purposes and should not be construed as an endorsement, recommendation, or solicitation to buy or sell securities. Past performance is not a guarantee of future results. 2 Spreads . What is an Option Spread? . An Example of a Vertical Debit Spread . Examples of Vertical Credit Spreads . How to choose strike prices when employing the Vertical Credit Spread strategy . Note: Any mention of Credit Spread today is using a Vertical Credit Spread. 3 A Spread A Spread is a combination trade, buying and/or selling two or more financial products. It could be stock and stock (long Coca Cola – short shares of Pepsi), Stock and Option (long Qualcomm, short a March QCOM call - many investors have used the “Covered Call”), maybe long an IBM call and Put.
    [Show full text]
  • Implied Index and Option Pricing Errors: Evidence from the Taiwan Option Market
    The International Journal of Business and Finance Research ♦ Volume 5 ♦ Number 2 ♦ 2011 IMPLIED INDEX AND OPTION PRICING ERRORS: EVIDENCE FROM THE TAIWAN OPTION MARKET Ching-Ping Wang, National Kaohsiung University of Applied Sciences Hung-Hsi Huang, National Pingtung University of Science and Technology Chien-Chia Hung, National Pingtung University of Science and Technology ABSTRACT This study examines both restricted and unrestricted Black-Sholes models, according to Longstaff (1995). Using the Taiwan index options for each day from January 2005 to December 2008, the unrestricted model simultaneously solves the implied index value and implied volatility whereas the restricted model only solves the implied volatility. Next, this study compares the pricing performance of restricted and unrestricted Black-Scholes models. The empirical results show he implied index value is almost higher than the actual index value. Moneyness has a significant negative impact on the index pricing error for calls but negative impact for puts. Open interest has a significantly negative impact on the index pricing error for calls. Volatility for calls has no significant effect on the index pricing error. The path-dependent effect on index pricing error increases with index returns. The unrestricted model has significantly less option pricing bias for calls than the restricted model. The option pricing error for calls in the restricted model has much larger negative bias near the middle maturity. The R-square in the restricted model is always much larger than the unrestricted model for both calls and puts. Finally, the option pricing errors are significantly affected by moneyness and time to expiration for all cases; this fact is consistent with Longstaff (1995).
    [Show full text]
  • Options Trading
    OPTIONS TRADING: THE HIDDEN REALITY RI$K DOCTOR GUIDE TO POSITION ADJUSTMENT AND HEDGING Charles M. Cottle ● OPTIONS: PERCEPTION AND DECEPTION and ● COULDA WOULDA SHOULDA revised and expanded www.RiskDoctor.com www.RiskIllustrated.com Chicago © Charles M. Cottle, 1996-2006 All rights reserved. No part of this publication may be printed, reproduced, stored in a retrieval system, or transmitted, emailed, uploaded in any form or by any means, electronic, mechanical photocopying, recording, or otherwise, without the prior written permission of the publisher. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold with the understanding that neither the author or the publisher is engaged in rendering legal, accounting, or other professional service. If legal advice or other expert assistance is required, the services of a competent professional person should be sought. From a Declaration of Principles jointly adopted by a Committee of the American Bar Association and a Committee of Publishers. Published by RiskDoctor, Inc. Library of Congress Cataloging-in-Publication Data Cottle, Charles M. Adapted from: Options: Perception and Deception Position Dissection, Risk Analysis and Defensive Trading Strategies / Charles M. Cottle p. cm. ISBN 1-55738-907-1 ©1996 1. Options (Finance) 2. Risk Management 1. Title HG6024.A3C68 1996 332.63’228__dc20 96-11870 and Coulda Woulda Shoulda ©2001 Printed in the United States of America ISBN 0-9778691-72 First Edition: January 2006 To Sarah, JoJo, Austin and Mom Thanks again to Scott Snyder, Shelly Brown, Brian Schaer for the OptionVantage Software Graphics, Allan Wolff, Adam Frank, Tharma Rajenthiran, Ravindra Ramlakhan, Victor Brancale, Rudi Prenzlin, Roger Kilgore, PJ Scardino, Morgan Parker, Carl Knox and Sarah Williams the angel who revived the Appendix and Chapter 10.
    [Show full text]