DOCSLIB.ORG

Modified Z-Scan Techniques for Investigations of Nonlinear Chiroptical Effects

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modified Z-Scan Techniques for Investigations of Nonlinear Chiroptical Effects Modified Z-scan techniques for investigations of nonlinear chiroptical effects Przemyslaw P. Markowicza), Marek Samoca,c), John Cerneb), Paras N. Prasada,b), Andrea Puccid) and Giacomo Ruggerid) a) Institute for Lasers, Photonics and Biophotonics b) Department of Physics State University of New York at Buffalo, Buffalo, NY 14260, USA c) Laser Physics Centre, Australian National University, Canberra, ACT 0200, Australia d) INSTM UdR Pisa c/o Dipartimento di Chimica e Chimica Industriale, Via Risorgimento 35, 56126 Pisa, Italy [email protected], [email protected], [email protected], [email protected], [email protected], [email protected] Abstract: We present simple modifications of the classic Z-scan technique for the investigations of nonlinear chiroptical effects, i.e. nonlinear circular birefringence and two-photon circular dichroism. Two methods for studying these effects: a “polarimetric Z-scan” and a “polarization modulated Z- scan” are described in detail. These techniques were applied to estimate the order of magnitude of the effects for several different materials. 2004 Optical Society of America OCIS codes: (190.4710) Optical nonlinearities in organic materials; References 1. P. N. Prasad. Introduction to biophotonics (Wiley & Sons, Hoboken, New Jersey, 2003). 2. I. Tinoco, Jr., "Two-photon circular dichroism," J. Chem. Phys. 62, 1006-1009 (1975). 3. E. A. Power, "Two-photon circular dichroism," J. Chem. Phys. 63, 1348-1350 (1975). 4. G. Wagniere, "Optical-activity of higher-order in a medium of randomly oriented molecules," J. Chem. Phys. 77, 2786-2792 (1982). 5. S. Kielich, "Nonlinear optical activity in liquids," Acta Physica Polonica 35, 861-862 (1969). 6. D. V. Vlasov and V. P. Zaitsev, "Experimental observation of nonlinear optical activity," Pis'ma Zh. Eksp. Teor. Fiz. 14, 171-175 (1971). 7. R. Cameron and G. C. Tabisz, "Observation of two-photon optical rotation by molecules," Mol. Phys. 90, 159-164 (1997). 8. F. Hache, H. Mesnil, M. C. Schanne-Klein, "Nonlinear circular dichroism in a liquid of chiral molecules: A theoretical investigation," Phys. Rev. B 60, 6405-6411 (1999). 9. H. Mesnil and F. Hache, "Experimental evidence of third-order nonlinear dichroism in a liquid of chiral molecules," Phys. Rev. Lett. 85, 4257-4260 (2000). 10. H. Mesnil, M. C. Schanne-Klein, F. Hache, M. Alexandre, G. Lemercier, C. Andraud, "Experimental observation of nonlinear circular dichroism in a pump-probe experiment," Chem. Phys. Lett. 338, 269-276 (2001). 11. H. Mesnil, M. C. Schanne-Klein, F. Hache, M. Alexandre, G. Lemercier, C. Andraud, "Wavelength dependence of nonlinear circular dichroism in a chiral ruthenium-tris(bipyridyl) solution," Phys. Rev. A 66, 013802 (2002). 12. J. Sztucki and W. Strek, "Two-photon circular dichroism in lanthanide(III) complexes," J. Chem. Phys. 85, 5547-5550 (1986). 13. K. E. Gunde and F. S. Richardson, "Fluorescence-detected two-photon circular dichroism of Gd3+ in trigonal Na3[Gd(C4H4O5)3].2NaClO4.6H2O," Chem. Phys. 194, 195-206 (1995). 14. M. Sheikh-bahae, A. A. Said, T. Wei, D. J. Hagan, E. W. v. Stryland, "Sensitive measurement of optical nonlinearities using a single beam," IEEE J. Quantum Electron. 26, 760-769 (1990). 15. A. Pucci, S. Nannizzi, G. Pescitelli, L. D. Bari, G. Ruggeri, "Chiroptical properties of terthiophene chromophores dispersed in oriented and unoriented polyethylene films," Macrom. Chemistry and Physics 205, 786-794 (2004). 16. D. H. Turner, I. Tinoco, M. Maestre, "Fluorescence detected circular-dichroism," J. Am. Chem. Soc. 96, 4340-4342 (1974). 17. X. Xie and J. D. Simon, "Picosecond circular dichroism spectroscopy: A Jones matrix analysis," J. Opt. Soc. Am. B 7, 1673-1684 (1990). #5140 - $15.00 US Received 27 August 2004; revised 6 October 2004; accepted 8 October 2004 (C) 2004 OSA 18 October 2004 / Vol. 12, No. 21 / OPTICS EXPRESS 5209 1. Introduction Optical isomers, i.e., molecules existing in two mirror image forms that cannot be superimposed by simple rotation (the phenomenon of chirality), commonly appear in all living organisms and their existence has very important consequences in biology and in biophotonics [1]. The properties of these molecules involve a slight difference in the interaction with left and right handed circularly polarized light. Such differences should also apply to nonlinear optical processes. There is already a great body of theoretical and experimental research on second-order nonlinear optical phenomena in chiral media. The studies of the combination of chirality with third-order (cubic) optical nonlinearity can further broaden our knowledge about light-matter interaction and may be of great practical interest as third-order effects are more general, requiring no special symmetry conditions. Theoretical description of the interaction of chiral molecules with high-intensity light has been carried out for quite some time [2-4] but the experimental evidence is scarce. As early as in 1969, Kielich discussed the theory of nonlinear optical rotation [5] and there are indications that this phenomenon has been observed [6,7]. In 1975, Tinoco [2] and Power [3] published independent papers on two- photon circular dichroism. Later, Wagniere [4] predicted that optical activity of higher order should be observable in various third-order optical nonlinearity related experiments. Recently, a French group [8-11] has provided extensive experimental and theoretical treatment of the case of chiral contribution to absorption saturation which may be considered as an effective χ(3) process in the sense that it is an intensity-dependent absorption. Nonlinear circular dichroism has also been reported for lanthanides [12,13]. In principle, a multitude of nonlinear optical phenomena can arise from the handedness of light-matter interaction. We limit the scope of this paper to two phenomena which may be treated either as the chirality-induced modifications of the cubic nonlinear optical properties or, alternatively, as the nonlinear part of the usual chiroptical properties, i.e. the circular birefringence (optical activity) and circular dichroism. For fully degenerate third-order nonlinear optical phenomena defined by the nonlinear refractive index, n2, and the nonlinear absorption coefficient, β, one can introduce their chiral counterparts as δn2,c and δβc where the δ symbol stands for the difference between the value of the parameter for right- and left- handed circular polarization. On the other hand, the nonlinear circular birefringence δn2,c can be treated as derived from the optical rotation strength coefficient [α] which can be considered intensity dependent, with the coefficient d[α]/dI being a measure of the nonlinearity. One can show that d[α]/dI = π/λ δn2,c . In a similar way, the nonlinear dichroism which is related to the imaginary part of the complex susceptibility, is δβc = d(δε)/dI, where δε is the linear circular dichroism expressed as the difference of absorption coefficients (ε) for right and left handed circularly polarized light. The estimation of the order of magnitude of the nonlinear chiroptical effects has been attempted in several theoretical papers. Wagniere [4] predicted that the chiral modulation of NLO effects (i.e. the relative difference between the values of a nonlinear coefficient for the left-handed and right-handed circularly polarized light) may be of the order of 10-2. Estimates given by other authors are between 10-4 and 10-2. Thus, the effects should be measurable using standard modulation techniques. A convenient and ingeniously simple technique for measuring intensity dependent effects like nonlinear absorption and refraction is that of Z- scan [14]. We propose here two modifications of this technique for detection of nonlinear chiroptical effects: the “polarimetric Z-scan” and the “polarization modulated Z-scan”. 2. Polarimetric Z-scan The “polarimetric” Z-scan is presented in Fig. 1. As in a simple polarimeter, placing an optically active sample between crossed polarizers results in appearance of light transmission. By rotating the analyzer by angle φ one can achieve the minimum transmission condition. However, as the optically active sample is translated along the z axis, the changing light intensity leads to reappearance of the transmission which peaks at the z=0 position, i.e. where #5140 - $15.00 US Received 27 August 2004; revised 6 October 2004; accepted 8 October 2004 (C) 2004 OSA 18 October 2004 / Vol. 12, No. 21 / OPTICS EXPRESS 5210 the intensity is the highest. This simple principle can be used to determine the nonlinear optical rotation, however, the appearance of increased transmission as the sample is near the focal plane of the lens may also be attributed to other effects causing depolarisation of the light transmitted through the sample. A necessary check that the light polarization plane has indeed been rotated is performing the Z-scan at analyzer positions rotated slightly off the crossing position. polarizerOpt. active sample analyzer D lens lens z Fig. 1. Principle of polarimetric Z-scan. Figure 2 shows an example of such a set of results obtained using 100 fs pulses at 650 nm (1 kHz repetition rate) and a solution of sucrose as a sample. The existence of the intensity dependent rotation of the polarization plane is confirmed by the characteristic “heterodyne” effect which is due to the light transmitted through the analyzer acting as a local oscillator when mixing with the transmission due to the nonlinear polarization rotation. The theoretical lines in the figures were calculated using the Malus law dφ P = P + P sin2Ω+ I(z) T S 0 dI where PT and P0 are the transmitted and incident power, Ω is the angle of rotation of the analyzer from the low intensity minimum position, dφ/dI is the nonlinearity of the optical rotation strength of the substance in the cell, and I(z) is the cell-position-dependent intensity calculated knowing the Rayleigh length of the beam, zR A small background transmitted power PS is due to scattering.
Load more

Recommended publications
  • Exp 1 - Separation of Limonene Name ______And Carvone, Due Date in Syllabus
    CHEM 8M, Binder UCSC Experiment 1 - Separation of Carvone and Limonene Reading Assignment Mohrig Chapter 19.1, 19.2, 19.5a, 19.7 (Liquid / Column Chromatography) Review Topics: Polarimetry (Chapter 17), TLC (Chapter 18), GC (Chapter 20) Terpenes encompass a large family of organic compounds widespread in nature and occurring in all organisms from bacteria to mammals. They are prevalent in plants, where they act as volatile chemical messengers to attract insects and also to defend the plant’s territory. Mixtures of volatile and scented compounds, very rich in terpenes, can be obtained by steam distillation of plant tissues (as in the isolation of citrus oils experiment). These mixtures are called essential oils. Carvone is a naturally occurring ketone found in the essential oils of caraway, dill, and spearmint in association with other terpenoids such as limonene. Limonene is found in spearmint, caraway, lemon, and orange oils. Carvone and limonene, both monoterpenes, have only one stereogenic center and can exist in two enantiomeric forms: R and S. Enantiomers have the same physical and chemical properties, except that they interact differently with polarized light and other chiral molecules. The two enantiomers of carvone have different smells, one fresh and minty, and the other sweet and somehow unpleasant, especially at high concentrations. The olfactory receptors that line our nasal mucus are chiral ensembles with an exquisite sensitivity to the size, shape, and chirality of the odorant. Their interaction with individual enantiomers is often specific, resulting in the production of distinctive smells. The odor difference between the two enantiomeric forms of carvone is obvious to most people.
    [Show full text]
  • The Optical Rotation of Liquids Its Variation with Wave Length Temperature, Solvent and Concentration
    U. S. DEPARTMENT OF COMMERCE BUREAU OF STANDARDS THE OPTICAL ROTATION OF LIQUIDS ITS VARIATION WITH WAVE LENGTH TEMPERATURE, SOLVENT AND CONCENTRATION By T. MARTIN LOWRY MISCELLANEOUS PUBLICATION No. 118 U. S. DEPARTMENT OF COMMERCE R. P. LAMONT, Secretary BUREAU OF STANDARDS GEORGE K. BURGESS, Director Miscellaneous Publication No. 118 THE OPTICAL ROTATION OF LIQUIDS ITS VARIATION WITH WAVE LENGTH TEMPERATURE, SOLVENT AND CONCENTRATION BY T. MARTIN LOWRY MARCH 25, 1932 UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON : 1932 For sale by the superintendent of Documents, Washington, d. c. PREFACE The compilation of the available data on this topic, as presented in the following pages, was made in conjunction with work undertaken for the International Critical Tables and covers, with the exceptions noted below, the literature preceding January 1, 1923. No attempt has been made to include fragmentary data. Data for the sodium D-line at ordinary temperatures and in the common solvents will be found in International Critical Tables. 1 The common sugars have also been omitted from the present compilation, since they have been covered in the saccharimetry section of International Critical Tables. 2 i Int. Crit. Tables, 7, pp. 355-489. McGraw-Hill Book Co., New York; 1931. » Int. Crit. Tables, 2, pp. 334-355. McGraw-Hill Book Co., New York; 1927. CONTENTS Page Preface n L Arrangement 1 II. Symbols and abbreviations 2 III. Class I. Organic substances in which the asymmetric carbon atom does not form part of a ring 2 IB. The molecule contains one carbon atom attached to four different atoms or groups 2 IBi.
    [Show full text]
  • The Optical Rotation of Liquids Its Variation with Wave Length Temperature, Solvent and Concentration
    U. S. DEPARTMENT OF COMMERCE BUREAU OF STANDARDS THE OPTICAL ROTATION OF LIQUIDS ITS VARIATION WITH WAVE LENGTH TEMPERATURE, SOLVENT AND CONCENTRATION By T. MARTIN LOWRY MISCELLANEOUS PUBLICATION No. 118 U. S. DEPARTMENT OF COMMERCE R. P. LAMONT, Secretary BUREAU OF STANDARDS GEORGE K. BURGESS, Director Miscellaneous Publication No. 118 THE OPTICAL ROTATION OF LIQUIDS ITS VARIATION WITH WAVE LENGTH TEMPERATURE, SOLVENT AND CONCENTRATION BY T. MARTIN LOWRY MARCH 25, 1932 UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON : 1932 For sale by the superintendent of Documents, Washington, d. c. PREFACE The compilation of the available data on this topic, as presented in the following pages, was made in conjunction with work undertaken for the International Critical Tables and covers, with the exceptions noted below, the literature preceding January 1, 1923. No attempt has been made to include fragmentary data. Data for the sodium D-line at ordinary temperatures and in the common solvents will be found in International Critical Tables. 1 The common sugars have also been omitted from the present compilation, since they have been covered in the saccharimetry section of International Critical Tables. 2 i Int. Crit. Tables, 7, pp. 355-489. McGraw-Hill Book Co., New York; 1931. » Int. Crit. Tables, 2, pp. 334-355. McGraw-Hill Book Co., New York; 1927. CONTENTS Page Preface n L Arrangement 1 II. Symbols and abbreviations 2 III. Class I. Organic substances in which the asymmetric carbon atom does not form part of a ring 2 IB. The molecule contains one carbon atom attached to four different atoms or groups 2 IBi.
    [Show full text]
  • An Evaluation of Four Commercial HPLC Chiral Detectors: a Comparison of Three Polarimeters and a Circular Dichroism Detector
    An evaluation of four commercial HPLC chiral detectors: A comparison of three polarimeters and a circular dichroism detector. by Laila Kott*, W. Brian Holzheuer, Megan M. Wong and Gregory K. Webster Analytical Research & Development Pfizer Global Research and Development 2800 Plymouth Road Ann Arbor, MI 48105 Keywords: Chiral HPLC detectors, circular dichroism detector, comparison of commercial polarimeters, ORD *Corresponding author. Tel: +1 734 622 4925; fax: +1 734 622 7711. Email address: [email protected] Manuscript Submitted to Journal of Pharmaceutical and Biomedical Analysis December 2005 1 ABSTRACT With increasing frequency, new drug candidates being introduced into pharmaceutical drug pipelines are chiral. Often only one enantiomer exhibits the desired biological activity and the other enantiomer may exhibit undesired side effects, thereby making chiral purity an important parameter. The introduction of chiral analysis adds additional complications in drug development. The pharmaceutical industry is constantly striving to streamline processes and improve efficiencies in an effort to move molecules to market quickly. In order to simplify the process of chiral method development, chiral screening can be set up, however a successful chiral screen depends on optimizing two factors: the column and the detector. The following work investigated the second factor and evaluated two types of commercially available chiral detectors for their possible use in chiral method development and screening: polarimeters and circular dichroism (CD) detectors. Linearity, precision, and the limit of detection (LD) of six compounds (trans-stilbene oxide, ethyl chrysanthemate, propranolol, 1-methyl-2-tetralone, naproxen, methyl methionine) on four commercial detectors (3 polarimeters and 1 CD detector) were determined experimentally and the limit of quantitation (LQ) calculated from the experimental LD.
    [Show full text]
  • Chirality: the Handedness of Molecules
    06 Chirality: The Handedness of Molecules Tartaric acid is found in grapes and other fruits, both free and as its salts (see Section 6.4B). Inset: A model of tartaric acid. (© fatihhoca/iStockphoto) KEY QUESTIONS 6.1 What Are Stereoisomers? 6.9 What Is the Significance of Chirality in the 6.2 What Are Enantiomers? Biological World? 6.3 How Do We Designate the Configuration of a 6.10 How Can Enantiomers Be Resolved? Stereocenter? HOW TO 6.4 What Is the 2n Rule? 6.1 How to Draw Enantiomers 6.5 How Do We Describe the Chirality of 6.2 How to Determine the R & S Configuration Cyclic Molecules with Two Stereocenters? without Rotating the Molecule 6.6 How Do We Describe the Chirality 6.3 How to Determine Whether Two Compounds Are of Molecules with Three or More the Same, Enantiomers, or Diastereomers without Stereocenters? the Need to Spatially Manipulate the Molecule 6.7 What Are the Properties of Stereoisomers? 6.8 How Is Chirality Detected in the CHEMICAL CONNECTIONS Laboratory? 6A Chiral Drugs IN THIS CHAPTER, we will explore the relationships between three-dimensional ob- jects and their mirror images. When you look in a mirror, you see a reflection, or mirror Mirror image The reflection image, of yourself. Now, suppose your mirror image becomes a three-dimensional object. of an object in a mirror. 167 168 CHAPTER 6 Chirality: The Handedness of Molecules We could then ask, “What is the relationship between you and your mirror image?” By relationship, we mean “Can your reflection be superposed on the original ‘you’ in such a way that every detail of the reflection corresponds exactly to the original?” The answer is that you and your mirror image are not superposable.
    [Show full text]
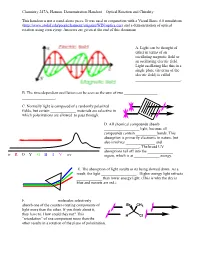
  • Optical Rotation Demonstration Handout
    Chemistry 247A, Hanson. Demonstration Handout—Optical Rotation and Chirality This handout is not a stand-alone piece. It was used in conjunction with a Visual Basic 6.0 simulation (http://www.stolaf.edu/people/hansonr/origami/WIN/optics.exe) and a demonstration of optical rotation using corn syrup. Answers are given at the end of this document. A. Light can be thought of either in terms of an oscillating magnetic field or an oscillating electric field. Light oscillating like this in a single plane (in terms of the electric field) is called _______________________. B. The time-dependent oscillation can be seen as the sum of two _________________ _________________. C. Normally light is composed of a randomly polarized fields, but certain _____________ materials are selective in which polarizations are allowed to pass through. D. All chemical compounds absorb __________________ light, because all compounds contain ___________bonds. This absorption is primarily electronic in nature, but also involves _______________ and __________________. The broad UV absorptions tail off into the _____________ ir R O Y G B I V uv region, which is at _____________ energy. E. The absorption of light results in its being slowed down. As a result, the light __________________. Higher energy light refracts _____________ than lower energy light. (This is why the sky is blue and sunsets are red.) F. _______________ molecules selectively absorb one of the counter-rotating components of Br CH3 light more than the other. If you think about it, they have to. How could they not? This H Cl ―retardation‖ of one component more than the other results in a rotation of the plane of polarization.
    [Show full text]
  • Chapter 6 Chirality: the Handedness of Molecules Table of Contents
    Chapter 6 Chirality: The Handedness of Molecules Table of Contents 1. Chirality and Stereochemistry (Chiral vs. achiral) 2. Isomerism: Constitutional Isomers and Stereoisomers 3. Enantiomers and Chiral Molecules 4. Molecules Having One Chirality Center Are Chiral 5. More about the Biological Importance of Chirality 6. How to Test for Chirality: Planes of Symmetry 7. Naming Enantiomers: The R,S-System 8. Properties of Enantiomers: Optical Activity 9. The Origin of Optical Activity 10. Chiral Drugs 11. Molecules with More than One Chirality Center 12. Fischer Projection Formulas 13. Stereoisomerism of Cyclic Compounds In this chapter we will consider: How to identify, codify, and name the three-dimensional arrangement of atoms and molecules How such arrangements can lead to unique properties and behaviors 1. Chirality & Stereochemistry An object is achiral (not chiral) if the object and its mirror image are identical chiral ! A chiral object is one that cannot be superposed on its mirror image Which are chiral objects? 1A. The Biological Significance of Chirality Chiral molecules are molecules that cannot be superimposed onto their mirror images ● One enantiomer causes birth defects, Thalomide the other cures morning sickness 66% of all drugs in development are chiral, 51% are being studied as a single enantiomer Of the $475 billion in world-wide sales of formulated pharmaceutical products in 2008, $205 billion was attributable to single enantiomer drugs O O CH3 CO2H Aspirine 2. Isomerisom: Constitutional Isomers & Stereoisomers 2A.
    [Show full text]
  • Circular Dichroism Investigations of Chiral Molecules in the Gas Phase
    TECHNISCHE UNIVERSITÄT MÜNCHEN Lehrstuhl für Physikalische Chemie Circular Dichroism Investigations of Chiral Molecules in the Gas Phase with a Laser-Mass Spectrometer Jörn Hendryk Thore Lepelmeier Vollständiger Abdruck der von der Fakultät für Chemie der Technischen Universität München zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften genehmigten Dissertation. Vorsitzender: Prof. Dr. Sebastian Günther Prüfer der Dissertation: 1. Prof. Dr. Ulrich K. Heiz 2. apl. Prof. Dr. Christoph Haisch Die Dissertation wurde am 21.11.2018 bei der Technischen Universität München eingereicht und durch die Fakultät für Chemie am 04.02.2019 angenommen. „For-thi loke thow lovye, As longe as thow durest; For is no science under sonne So sovereyn for the soule.“ - William Langland - CREDIT: UNIVERSITY OF NOTTINGHAM1 „So long as you live, see that you love, For no science under the sun can so heal the soul.” - modern translation by Terrence Tiller - Table of Content A. Abstract ......................................................................................................................... - 1 - 1. Introduction ................................................................................................................... - 5 - 1.1. Chirality - A Fundamental Component of Life .............................................. - 6 - 1.2. Analyzing of Chiral Molecules ..................................................................... - 9 - 1.2.1. Optical Techniques .........................................................................
    [Show full text]
  • Download (4MB)
    THESIS, WITH ADDITIONAL PAPER PRESENTED ALEXANDER HUGE LAMBERTGN, B Sc. FOR THE DEGREE OF Ph.D. Organic Chemistry Department, University of Glasgow. June, 1936. ProQuest Number: 13905232 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 13905232 Published by ProQuest LLC(2019). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 TO My MOTHER. I am deeply indebted to my supervisor, Professor T. S. Patterson, for his advice and assistance. I acknowledge gratefully the receipt of a Mackay Smith Scholarship from the University of Glasgow, and a Research Scholarship from the Carnegie Trust. The majority of the (.micro) nitrogen determinations were carried out by Mr. J. M. L. Cameron, of the Organic Chemistry Department of this University. The remainder of the analyses quoted were due to Dr. G. Weiler, of Oxford. INDEX n Paragraphs11 Page. Titles 1,2 & 82 The Reciprocal Solvent Effect of Some Optically Active Compounds 1 to 56 2-81 A. Introduction 1-2 3 B. Historical 3-11 5 C. Theoretical 12 to 35 14 (ii The Recognition of Mutual Solvent Influence 13 ♦ 15 14 (ii) Recognition of Asymmetric Solvent Influence 16-34 17 (iii) Summary 35 32 D.
    [Show full text]
  • Exp 1 - Separation of Limonene Name ______And Carvone
    CHEM 108M, Binder UCSC Experiment 1 - Separation of Carvone and Limonene Reading: Mohrig Section 18 Terpenes encompass a large family of organic compounds widespread in nature and occurring in all organisms from bacteria to mammals. They are prevalent in higher plants, where they act as volatile chemical messengers to attract insects and also to defend the plant’s territory. Mixtures of volatile and odoriferous compounds, very rich in terpenes, can be obtained by steam distillation of plant tissues (as in the isolation of citrus oils experiment). These mixtures are called essential oils. In this experiment, you will separate carvone and limonene from the essential oil of either spearmint or caraway by column chromatography, a type of adsorption chromatography. The principles of column chromatography and TLC are identical. The stationary phase is silica (SiO2) and the mobile phase is an organic solvent. In this experiment, you will pack a microcolumn with silica gel and use an eluotropic series of hexanes and acetone to separately elute carvone and limonene. As in TLC analysis, this separation is based on polarity. The only difference is in the direction of the movement of the mobile phase. In TLC, the solvent (mobile phase) moves by capillary action against gravity. In column chromatography, the mobile phase is added to the top of the column and moves down with gravity. The stationary phase (silica) is polar and will hold onto the more polar compounds longer. In other words, the less polar compounds in a mixture will elute first. The solvent collected at the bottom of the column can be collected and separated over time.
    [Show full text]
  • Organic Chemistry Laboratory I Extraction of (+) and (-)-Carvone from Oil of Caraway and Oil of Spearmint Experiment Description & Background
    Organic Chemistry Laboratory I Extraction of (+) and (-)-Carvone from Oil of Caraway and Oil of Spearmint Experiment Description & Background Introduction Students will purify and isolate limonene and either (+)-carvone from oil of caraway or (-)-carvone from oil of spearmint using column chromatography. The isolated carvone and limonene will be identified by comparison with standards using thin layer chromatography (TLC) , infrared (IR) spectroscopy, and the optical rotation of the isolated carvone will be determined by polarimetry. Oil of Spearmint and Oil of Caraway Essential oils, derived from natural products, have been used for centuries as flavorings, fragrances and for medicinal purposes. These oils typically contain multiple organic components, generally with one or more compounds dominating the mixture to provide characteristic odor and properties. Essential oils are typically isolated from plant sources through distillation or extraction. Oil of spearmint is derived from the leaves of the spearmint (Mentha spicata) plant. A major constituent of oil of spearmint is the R enantiomer of carvone. Minor amounts of limonene, a metabolic precursor of carvone is also present in oil of spearmint. Caraway oil is extracted from caraway seeds (Carum carvi) and contains manily the S enantiomer of carvone along with higher levels of limonene. The limonene in oil of caraway is also a precuror to S-carvone. Specific carvone enantiomers can be isolated in pure form from oil of spearmint or oil of caraway using column chromatography. Limonene, a less polar constituent of these essential oils can be separated from the carvones Spearmint during chromatography. Purity of the isolated samples can be evaluated by thin layer chromatography and Caraway spectroscopic analysis, and the optical purity of the enatiomers can be evaluated using polarimetry.
    [Show full text]
  • Assigned Readings
    CHEM 221 section 01 LECTURE #18 Thurs., Nov.03, 2005 ASSIGNED READINGS: TODAY’S CLASS: continue Ch.5 NEXT LECTURE: finish Ch.5 http://artsandscience.concordia.ca/facstaff/P-R/rogers (1) 5.5 Drawing enantiomers perspective drawings: use dashes & wedges to show 3D geometry • practice: drawing & rotating molecules on paper & in your head… To draw a molecule’s enantiomer: 1. Draw molecule as a perspective drawing • only need to show all 3D information for asymmetric atoms 2. Imagine reflecting molecule in a mirror • configuration of EVERY asymmetric atom will be inverted 3. Check: is this really a different compound? • original & mirror image are only enantiomers if they are nonsuperimposable mirror images of each other CH3 H3C rotate CH3 * * CH2CH3 H3CH2C CH2CH3 H H H HO HO H OH OH HO H Draw its Can now see: enantiomer… mirror configuration opposite to original Shortcut: to draw a chiral C (i.e., C*) with opposite configuration, detach any 2 groups from that C* & switch their places (2) 5.9 Diastereomers (stereoisomers that are not mirror images) Æ only SOME of their stereocentres have opposite configuration cis /trans isomers: NOT mirror images at this point (C’s with same configuration) Mirror images at this point (C’s with opposite configuration) Each one here is achiral: each has a horizontal internal mirror plane thus: each is superimposable on its own mirror image thus: neither molecule has an enantiomer compounds with chiral centres: Mirror images at this point (C’s with opposite configuration) NOT mirror images at this point (C’s with same configuration) Achiral: Chiral: no internal mirror plane internal mirror plane does have an enantiomer (not shown) (3) Perspective drawings vs.
    [Show full text]