Notes on HF Discone Antennas
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Antenna Theory and Design SECOND EDITION
Antenna Theory and Design SECOND EDITION Warren L. Stutzman Gary A. Thiele WILEY Contents Chapter 1 • Antenna Fundamentals and Definitions 1 1.1 Introduction 1 1.2 How Antennas Radiate 4 1.3 Overview of Antennas 8 1.4 Electromagnetic Fundamentals 12 1.5 Solution of Maxwell's Equations for Radiation Problems 16 1.6 The Ideal Dipole 20 1.7 Radiation Patterns 24 1.7.1 Radiation Pattern Basics 24 1.7.2 Radiation from Line Currents 25 1.7.3 Far-Field Conditions and Field Regions 28 1.7.4 Steps in the Evaluation of Radiation Fields 31 1.7.5 Radiation Pattern Definitions 33 1.7.6 Radiation Pattern Parameters 35 1.8 Directivity and Gain 37 1.9 Antenna Impedance, Radiation Efficiency, and the Short Dipole 43 1.10 Antenna Polarization 48 References 52 Problems 52 Chapter 2 • Some Simple Radiating Systems and Antenna Practice 56 2.1 Electrically Small Dipoles 56 2.2 Dipoles 59 2.3 Antennas Above a Perfect Ground Plane 63 2.3.1 Image Theory 63 2.3.2 Monopoles 66 2.4 Small Loop Antennas 68 2.4.1 Duality 68 2.4.2 The Small Loop Antenna 71 2.5 Antennas in Communication Systems 76 2.6 Practical Considerations for Electrically Small Antennas 82 References 83 Problems 84 Chapter 3 • Arrays 87 3.1 The Array Factor for Linear Arrays 88 3.2 Uniformly Excited, Equally Spaced Linear Arrays 99 3.2.1 The Array Factor Expression 99 3.2.2 Main Beam Scanning and Beamwidth 102 3.2.3 The Ordinary Endfire Array 103 3.2.4 The Hansen-Woodyard Endfire Array 105 3.3 Pattern Multiplication 107 3.4 Directivity of Uniformly Excited, Equally Spaced Linear Arrays 112 3.5 Nonuniformly -

2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI National Radio Science Meeting
2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI National Radio Science Meeting Final Program 7–12 July 2019 Hilton Atlanta Atlanta, Georgia, U.S.A. Conference at a Glance Saturday, July 6 14:00-16:00 Strategic Planning Committee 16:15-17:15 AP-S Meetings Committee 17:15-18:15 JMC Meeting (Closed Session) 18:15-21:30 JMC Meeting, Dinner and Presentations 19:15-21:15 IEEE AP-S Constitution and Bylaws Committee Meeting & Dinner Sunday, July 7 08:00-10:00 Past Presidents’ Breakfast 10:00-18:00 AdCom Meeting 19:30-22:00 Welcome Dessert Reception at the Georgia Aquarium Monday, July 8 07:00-08:00 Amateur Radio Operators Breakfast 08:00-11:40 Technical Sessions 09:00-18:00 Technical Tour - “An Engineer’s Eye View” of the Mercedes Benz Stadium 12:00-13:20 Transactions on Antennas and Propagation Editorial Board Lunch Meeting 13:20-17:00 Technical Sessions 17:00-18:00 URSI Commission A Business Meeting 17:00-18:00 URSI Commission B Business Meeting 17:00-18:00 URSI Commissions C/E (combined) Business Meeting Tuesday, July 9 07:00-08:00 AP Magazine Staff Meeting 07:00-08:00 APS 2020 Committee Meeting 07:00-08:00 Industrial Initiatives 07:00-08:00 Membership Committee Meeting 07:00-08:00 Student Design Contest (Set-Up - Closed to Others) 07:00-08:00 Technical Committee on Antenna Measurement 08:00-11:40 Student Paper Competition 08:00-11:40 Technical Sessions 08:00-09:30 Student Design Contest (Demo for Judges - Closed to Others) 08:30-14:00 Standards Committee Meeting 09:30-12:00 Student Design Contest (Demo for Public) -

Practical Radio-Frequency Handbook
Practical Radio-Frequency Handbook Practical Radio-Frequency Handbook Third edition IAN HICKMAN BSc (Hons), CEng, MIEE, MIEEE Newnes OXFORD AUCKLAND BOSTON JOHANNESBURG MELBOURNE NEW DELHI Newnes An imprint of Butterworth-Heinemann Linacre House, Jordan Hill, Oxford OX2 8DP 225 Wildwood Avenue, Woburn, MA 01801–2041 A division of Reed Educational and Professional Publishing Ltd A member of the Reed Elsevier plc group First published 1993 as Newnes Practical RF Handbook Second edition 1997 Reprinted 1999 (twice), 2000 Third edition 2002 © Ian Hickman 1993, 1997, 2002 All rights reserved. No part of this publication may be reproduced in any material form (including photocopying or storing in any medium by electronic means and whether or not transiently or incidentally to some other use of this publication) without the written permission of the copyright holder except in accordance with the provisions of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London, England W1P 0LP. Applications for the copyright holder’s written permission to reproduce any part of this publication should be addressed to the publishers British Library Cataloguing in Publication Data Hickman, Ian Practical Radio-Frequency Handbook I. Title 621.384 ISBN 0 7506 5369 8 Cover illustrations, clockwise from top left: (a) VHF Log periodic antenna; (b) selection of RF coils; (c) HF receiver; (d) spectrum of IPAL TV signal with NICAM (Courtesy of Thales (a and (c)); Coilcraft -

MFJ 2004 Ham Buyers Guide
QSTCatP01.qxd 10/16/2003 10:03 AM Page 1 MFJ 2004 Ham Buyers Guide See inside for these New MFJ Products! 300W Automatic Tuner Tiny Travel Tuner DC Multi-Outlet Strips Ultra-fast, 2000 memories, antenna Fits in the palm of your hand! 150 has both 5-way binding posts switch, 4:1 balun, Cross-Needle and Watts, 80-10 Meters, Bypass Switch and Digital SWR/Wattmeter, 1.8-30 MHz Anderson PowerPole® connectors MFJ-902 $7995 $ 95 MFJ-1129 $ 95 109 MFJ-993 259 Four New models -- balun, Four new high current 150, 300, 600 Watt models. SWR/Wattmeter . DC multi-outlet strips . See Back Cover See Page 6 See Page 16 Balanced Line Dummy Load Manual Mic/Radio Switch Antenna Tuner SWR/Wattmeter Screwdriver Switch any 2 mics 1.5kW, to any 2 rigs Superb Antenna peak reading Covers 40-2 Meters balance, switchable 1.8-54 MHz, to external MFJ-1662 $ 95 $ 95 300 Watts antenna 129 MFJ-1263 99 $ 95 $ 95 MFJ-974H 189 MFJ-267 149 Four new models . Three new models . See Page 7 See Page 9 See Page 42 See Page 21 10 foot Antenna 160-6 Meter 1.5 kW 4:1 Glazed 4 Foot Telescopic Tripod Doublet current balun ceramic Ground Whip 40-inch Antenna /insulator insulator Rod MFJ-1954 between legs Copper bonded steel MFJ- $ 95 MFJ-1918 MFJ-919 MFJ-16C01 MFJ-1934 19 1777 $ 95 $ 95 $ 95 59 $ 95 3 lengths . 39 49 69c 4 See Page 42 See Page 42 See Page 43 See Page 43 See Page 43 See Page 7 Mobile Discone Atomic Atomic Wireless Speaker/Mic Antennas Antenna 24/12 Clock 24/12 Watch Weather for Yaesu VX-7R MFJ-1456, $14995 25-1300 Station MHz 40/20/15/10/6/2M MFJ- MFJ- MFJ-295R $ 95 $ 95 MFJ-1868 132RC 186RC MFJ-192 MFJ-1438, 99 $ 95 19 10/6/2M/440 MHz $5995 $1495 $2995 59 See Page 41, 39 See Page 40 See Page 29 See Page 30 See Page 30 See Page 35 Ameritron Ameritron Ameritron Hy-Gain Screwdriver Digital Screwdriver flat Mobile 80-10 M Vertical Antenna Antenna Controller SWR/Wattmeter The Classic is Back! 5 1.2 kW, Pittman Super bright high- Just 1 /8” thick, AV-18AVQII Commercial Gear Motor intensity LEDs flat mounts on $ 95 dashboard 229 SDA-100 SDC-100 MK-80, $79.95. -

Sensitive Ambient RF Energy Harvesting
Sensitive Ambient RF Energy Harvesting A thesis submitted in fulfilment of the requirements for the degree of Doctor of Philosophy Negin Shariati Bachelor of Engineering – Electrical and Electronics School of Electrical and Computer Engineering College of Science, Engineering and Health RMIT University August 2015 Declaration I certify that except where due acknowledgement has been made, the work is that of the author alone; the work has not been submitted previously, in whole or in part, to qualify for any other academic award; the content of the thesis is the result of work which has been carried out since the official commencement date of the approved research program; any editorial work, paid or unpaid, carried out by a third party is acknowledged; and, ethics procedures and guidelines have been followed. Negin Shariati 22 August 2015 i To the World Acknowledgements The outcomes presented in this thesis could not have been completed without the support of my supervisors. I would like to express my sincere gratitude to Prof. Kamran Ghorbani, A. Prof. Wayne Rowe and A. Prof. James Scott for their expert supervision, for the opportunity to work alongside them and for their valuable input on this research and academic writing. Greatest appreciation for my senior supervisor Prof. Kamran Ghorbani for promoting forward thinking and for his invaluable guidance and support during this PhD program. A great acknowledgement for Mr. David Welch as the most creative and skilled technical staff member for assistance in fabrication of the rectifier circuits. I would like to acknowledge Dr. Thomas Baum for his input and proof reading of this thesis. -

All About the Discone Antenna: Antenna of Mysterious Origin And
All About the Discone Antenna: Antenna of Mysterious Origin and Superb Broadband Performance Learn about the development, history and some applications of a discone antenna. Steve Stearns, K6OIK he frequency bandwidths as extensions of it.1 The discone antenna ent on the discone antenna. Kandoian’s novel “ demanded by high-definition (Figure 1) is one such extension, in which the or inventive element was apparently that the T television have considerable biconical dipole is asymmetric, one cone’s antenna could be encased in a radome, making range…” With these prescient words, Philip angle being 90°, which gives a flat disk of ra- it suitable for aircraft, not that it used a cone or S. Carter of RCA opened a 1939 paper that dius equal to the cone length. Two years later, disk per se, those ideas being obvious in view compared a variety of antennas for the emerg- in 1943, Armig Kandoian at the Federal Tele- of Schelkunoff’s prior work. The patent was ing field of “high-definition” television. Carter phone and Radio Corporation applied for a pat- granted in 1945, whereupon Kandoian and his showed conclusively that conical antennas colleagues, Sichak, Felsenheld, and Nail, at held distinct advantages over dipoles and fold- 1Notes appear on page 43. the newly renamed Federal Telecommunica- ed dipoles when it comes to broadband perfor- mance. Today, conical antennas are making a comeback for broadband applications such as digital television and UWB (ultra-wideband) or impulse radio. Stacked arrays of bowties and biconical dipoles are gradually displacing traditional mainstay antennas such as Yagis and log-periodics for the rooftop reception of digital television (DTV). -

Design of a Wideband Conformal Array Antenna System with Beamforming and Null Steering, for Application in a DVB-T Based Passive Radar
________________________________________________________________________________ Design of a wideband conformal array antenna system with beamforming and null steering, for application in a DVB-T based passive radar Master of Science Thesis Vedaprabhu Basavarajappa Student number: 4121910 03-July-2012 Supervisors: Dr. Massimiliano Simeoni and Dr. Peter Knott _________________________________________________________________________________ 2 Delft University of Technology Department of Telecommunications The undersigned hereby certify that they have read and recommend to the Faculty of Electrical Engineering, Mathematics and Computer Science for acceptance a thesis entitled “Design of a wideband conformal array antenna system with beamforming and null steering, for application in a DVB-T based passive radar”, by Vedaprabhu Basavarajappa in partial fulfilment of the requirements for the degree of Master of Science in Electrical Engineering. Dated: 03-July-2012 Committee members ____________________________ Prof. Dr. A. Yaravoy (Chair) ____________________________ Dr. M. Simeoni ____________________________ Dr. P. Knott _____________________________ Dr. Ir. B. J. Kooij ____________________________ Dr.ing. I.E. Lager 3 Acknowledgments I would like to express my sincerest thanks to Dr. Peter Knott who was my supervisor at Fraunhofer FHR for his constant support and encouragement. I am very grateful to my supervisor at TU Delft, Dr. Massimiliano Simeoni for having provided this opportunity and for his constant support and motivation and for providing valuable feedback to my work at Fraunhofer FHR. I would also like to extend my heartiest thanks to my graduation professor Prof. Dr. Alexander Yaravoy for his support and for his valuable feedbacks. I would also like to thank Dr. Daniel O’ Hagan of PSK group at FHR for his valuable inputs. I would like to extend my thanks to my friends at Fraunhofer FHR for having provided me with a wonderful atmosphere where I could carry out my thesis. -

Broadband Base Station Antenna the FXDP100-156 Is Designed for Excellent Omnidirectional Coverage Throughout the VHF Band of 100-156 Mhz
Model Name Frequencies FXMP2X15 2-30 MHz FXLP20X5 20-100 MHz FXLP25X4 25-90 MHz FXDC25X4 25-100 MHz FXDC30X3 30-90 MHz FXLP30X3 30-110 MHz FXLP30X17 30-512 MHz FXLP43-53 43-53 MHz FXLP88X7 88-600 MHz FXLP88X11 88-1000 MHz FXLP90X5 90-512 MHz FXDP100-156 100-156 MHz FXMP100X4 100-400 MHz FXDP100X4 100-400 MHz FXDC100X5 100-500 MHz FXLP100X10 100-1000 MHz FXDP100X25 100-2500 MHz FXDC113X4 113-420 MHz FXDP225X2 225-400 MHz FXDP225X2AB 225-400 MHz FXLP225X2 225-450 MHz FXLP225X2AB 225-512 MHz TACTICAL HUB OMNIDIRECTIONAL SERIES 340-6000 MHz FXLP500X5 500-2500 MHz FXLP500X5AB 500-2500 MHz FXLP800X3 800-2100 MHz FXSP806-960-12 806-960 MHz FXCL920-1785 900-940 1755-1815 MHz FXLP1200X2 1200-2000 MHz FXDP1800-1830 1800-1830 MHz FXSP1.8-2.1-12 1800-2100 MHz FXDP2.2-2.4 & 4.8-5.2-7-D 2200-2400 & 4800-5200 MHz FXDP2.3-2.5-7-D 2300-2500 MHz FXDP2.3-2.5-7 & 1710-2170 2300-2500 & 1710-2170 MHz FXDP4.4-4.9-7-D 4400-4900 MHz FXDP4.4-4.9-9-D 4400-4900 MHz FXDP4.4-5.0-7-D 4400-5000 MHz FXDP4.4-5.0-9-D 4400-5000 MHz FXDP5.0-6.0-7-D 5000-6000 MHz FXDP5.0-6.0-7-DAB 5000-6000 MHz FXDP5.0-6.0-7-DAC 5000-6000 MHz FXSP5.0-6.0 5000-6000 MHz FXSP5.0-6.0-D-HV 5000-6000 MHz SERIES II DIPLEXER 20-512 MHz 2-30 MHz FXMP2X15 Transportable Stake Antenna The FXMP2X15 is a portable 2-30 MHz base station antenna that includes nine sections of radiator that are hand tightened together, a ground radial kit and two guying assemblies. -

A Prototype Skeleton Discone Antenna for 2Nd and 3Rd Generation Mobile
Broadband radial discone antenna: Design, application and measurements N.I. Yannopoulou, P.E. Zimourtopoulos and E.T. Sarris The wide band of frequencies that includes all those allocated to 2G/3G applications was defined as 2G/3G band and the discone antenna with a structure of radial wires was defined as radial discone. This antenna was theoretically analysed and software simulated with the purpose of computationally design a broadband model of it. As an application, a radial discone for operation from 800 to 3000 MHz, which include the 2G/3G band, was designed and an experimental model was built and tested. Mathe- matically expressed measurement error bounds were computed in order to evaluate the agreement between theory and practice. Introduction: Kandoian invented the well-known discone antenna in 1945 [1]. Nail gave two simple relations for discone dimensions in 1953 [2]. Rappaport designed discones using an N-type connector feed in 1987 [3]. Cooke studied a discone with a structure of radial wires in 1993 [4]. Kim et al. recently presented a double radial dis- cone antenna for UWB applications [5]. This Letter proposes a broadband radial dis- cone fed by an N-type connector for operation from 800 to 3000 MHz that includes all frequencies allocated to 2G/3G applications. Analysis, Simulation, Design, Application and Measurements: The radial discone was theoretically analysed as a group of identical filamentary V-dipoles with unequal arms connected in parallel. The dipoles recline on equiangular vertical phi-planes around z-axis to form a disc-conical array. Fig. 1-A shows two coplanar dipoles conformed to the apex angle (a). -

COMPOSITE DISCAGE ANTENNA DEVELOPED for 2-TO-30-MC/S BAND Provides Omnidirectional Coverage in Horizontal Plane with VSWR of 3 to 1 Or Better S.E
- I SI "• COMPOSITE DISCAGE ANTENNA DEVELOPED FOR 2-TO-30-MC/S BAND Provides omnidirectional coverage in horizontal plane with VSWR of 3 to 1 or better S.E. Parker, L.G. Robbins, Research and Development Report 8 August 1967 and W.J.E. Edwards CLEAPlINGHOUSEC>L I 'GH0 L(P I THIS D3.CUMENT HAS BEEN APPROVED FOR PUBLIC RELEASE AND SALE; ITS DISTRIBUTICN IS UNLIMITED. It I! Ii PROBLEM Develop a 2-to-30-Mc 's antenna with impedance and pattern characteristics that are satisfactory for general ship and shore applications. RESULTS 1, A composite discone-cage vertically polar; ,-d antenna has been developed. It provides a VSWR of 3 to I or better throughout the 2-to-30-Mc/s band. Its coverage in the horizontal plane is omnidirectional. 2. Scale-model measairements demonstrate that low-angle radiation is provided by the cage section at most frequencies from 2 to 8 Mc/s., The discone section, owing to its elevated feed point, gives multilebed vertical patterns with a major lobe at relatively low angles fron 8 to 30 Mc's and higlwi.• 3. Auxiliary low-pass and high-pass networks can be used to isclate the antenna sections and to obtain favorable impedance transformations.. These networks in- sure that impedance and pattern characteristics will remain stable and predictable. RECOMMENDATIONS 1., Utilize the general-purpose DISCAGE antenna for ship and shore applications requiring an extremely versatile broadband antenna with omnidirectional character- istics. 2. Employ auxiliary low-pass and high-pass networks to obtain highly stable im- pedance and pattern characteristics, particularly when simultaneous operation of the cage and discone sections is required., 3. -
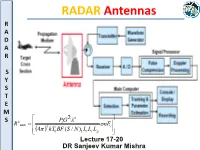
Lecture 17-20: Radar Antennas
RADAR Antennas R A D A R S YS YS TS TE ME 2 2 MS 4 PtG R max nE S 4 3 kT BF (S / N) L L L i 0 1 t r p Lecture 17-20 DR Sanjeev Kumar Mishra Antenna: R • An antenna is A • an electromagnetic radiator, D • a sensor, A • a transducer and R • an impedance matching device • For Radar Application, A directive antenna which concentrates the S energy into a narrow beam. Y • Most popularly used antennas are: Parabolic Reflector Antennas S T • Planar Phased Arrays E • Electronically steered Phased array M antennas S • A typical antenna beamwidth for the detection or tracking of aircraft might be about 1 or 2°. R • An antenna is defined by Webster’s Dictionary as “a usually metallic A device (as a rod or wire) for radiating or receiving radio waves.” D A • The IEEE Standard Definitions [IEEE Std 145–1983]: Antenna (or R aerial) “a means for radiating or receiving radio waves.” S YS YS TS TE ME MS S E & H Fields surrounding an Antenna Antenna as a transition device R A D A R S YS YS Transmission-line Thevenin equivalent of antenna in transmitting mode TS Z A RA jX A TE (R R ) jX ME r L A MS Where ZA : antenna impedance R : Antenna resistance S A Rr : radiation resistance RL :loss resistance (i.e. due to conduction & dielectric losses) XA : equivalent antenna reactance ANTENNA PARAMETERS R • Circuit Parameters A • Input Impedance D • Radiation Resistance A R • Antenna Noise Temperature • Return Loss S • Impedance bandwidth YS • Physical Quantities • Electromagnetic Parameters YS TS • Size • Field Pattern (Beam Area, TE • Weight Directivity, -

Model Name Frequencies
Model Name Frequencies TDMP001 000-000 MHz TDMP002 000-000 MHz TDYA216 000-000 MHz TDMP2X15 & TDMP3X10 2-30 & 3-30 MHz MPDP2X15AB 2-30 MHz TDLP90X5 90-500 MHz TDBC100X5 100-512 MHz TDDC113X4 113-420 MHz TDLP136-174 136-174 MHz SAMP138-153 138-153 MHz TDGP138-153 138-153 MHz SAMP146-313 138-153 & 310-315 MHz TDGP146-313 138-153 & 310-315 MHz TDLP200X3 200-600 MHz MVST240-320AB 240-320 MHz SAMP250-325 250-325 MHz TDGP250-325 250-325 MHz SADP902-928 902-928 MHz "RTDP" Rapid Tactical Deployable Series 2200-6000 MHz SERIES II DIPLEXER 20-512 MHz Customer Specified MHz TDMP001 Telescoping Antenna The TDMP001 antenna is a single frequency telescoping tactical antenna that is designed to meet submersible depth requirements of 65 ft. (20 m). The antenna is a center loaded, telescoping, stainless steel radiator encased in a rugged black polycarbonate tubular case. By unscrewing the captivated end caps the antenna can be fully extended to a length of 56.5 in. (1.44 m) and mounted to an electronics device with a matching connector. The stowed dimensions are 9 in. (229 mm) at a net weight of 0.5 lb. (0.23 kg) Made in the USA P.O. Box 909, Palmetto, Florida 34220-0909 ISO 9001:2008 Certified Tel: 941-723-2833 • Fax: 941-723-1628 (1Y02950) www.hascall-denke.com Customer Specified MHz TDMP001 Telescoping Antenna Specifications ELECTRICAL: Frequency Range: Customer Specified Gain: Customer Specified VSWR: Customer Specified Input Impedance: 50 Ω Nominal Power: 25 Was Polarizaon: Vercal Radiaon Paern: Azimuth: 360° Elevaon: 90° Input Connector: 1/4‐28UNF Thread MECHANICAL: Overall Height: 56.5 in.