Squibs and Discussions: Memoization in Top-Down Parsing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Design and Evaluation of an Auto-Memoization Processor
DESIGN AND EVALUATION OF AN AUTO-MEMOIZATION PROCESSOR Tomoaki TSUMURA Ikuma SUZUKI Yasuki IKEUCHI Nagoya Inst. of Tech. Toyohashi Univ. of Tech. Toyohashi Univ. of Tech. Gokiso, Showa, Nagoya, Japan 1-1 Hibarigaoka, Tempaku, 1-1 Hibarigaoka, Tempaku, [email protected] Toyohashi, Aichi, Japan Toyohashi, Aichi, Japan [email protected] [email protected] Hiroshi MATSUO Hiroshi NAKASHIMA Yasuhiko NAKASHIMA Nagoya Inst. of Tech. Academic Center for Grad. School of Info. Sci. Gokiso, Showa, Nagoya, Japan Computing and Media Studies Nara Inst. of Sci. and Tech. [email protected] Kyoto Univ. 8916-5 Takayama Yoshida, Sakyo, Kyoto, Japan Ikoma, Nara, Japan [email protected] [email protected] ABSTRACT for microprocessors, and it made microprocessors faster. But now, the interconnect delay is going major and the This paper describes the design and evaluation of main memory and other storage units are going relatively an auto-memoization processor. The major point of this slower. In near future, high clock rate cannot achieve good proposal is to detect the multilevel functions and loops microprocessor performance by itself. with no additional instructions controlled by the compiler. Speedup techniques based on ILP (Instruction-Level This general purpose processor detects the functions and Parallelism), such as superscalar or SIMD, have been loops, and memoizes them automatically and dynamically. counted on. However, the effect of these techniques has Hence, any load modules and binary programs can gain proved to be limited. One reason is that many programs speedup without recompilation or rewriting. have little distinct parallelism, and it is pretty difficult for We also propose a parallel execution by multiple compilers to come across latent parallelism. -
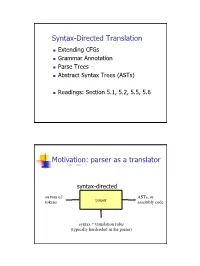
Syntax-Directed Translation, Parse Trees, Abstract Syntax Trees
Syntax-Directed Translation Extending CFGs Grammar Annotation Parse Trees Abstract Syntax Trees (ASTs) Readings: Section 5.1, 5.2, 5.5, 5.6 Motivation: parser as a translator syntax-directed translation stream of ASTs, or tokens parser assembly code syntax + translation rules (typically hardcoded in the parser) 1 Mechanism of syntax-directed translation syntax-directed translation is done by extending the CFG a translation rule is defined for each production given X Æ d A B c the translation of X is defined in terms of translation of nonterminals A, B values of attributes of terminals d, c constants To translate an input string: 1. Build the parse tree. 2. Working bottom-up • Use the translation rules to compute the translation of each nonterminal in the tree Result: the translation of the string is the translation of the parse tree's root nonterminal Why bottom up? a nonterminal's value may depend on the value of the symbols on the right-hand side, so translate a non-terminal node only after children translations are available 2 Example 1: arith expr to its value Syntax-directed translation: the CFG translation rules E Æ E + T E1.trans = E2.trans + T.trans E Æ T E.trans = T.trans T Æ T * F T1.trans = T2.trans * F.trans T Æ F T.trans = F.trans F Æ int F.trans = int.value F Æ ( E ) F.trans = E.trans Example 1 (cont) E (18) Input: 2 * (4 + 5) T (18) T (2) * F (9) F (2) ( E (9) ) int (2) E (4) * T (5) Annotated Parse Tree T (4) F (5) F (4) int (5) int (4) 3 Example 2: Compute type of expr E -> E + E if ((E2.trans == INT) and (E3.trans == INT) then E1.trans = INT else E1.trans = ERROR E -> E and E if ((E2.trans == BOOL) and (E3.trans == BOOL) then E1.trans = BOOL else E1.trans = ERROR E -> E == E if ((E2.trans == E3.trans) and (E2.trans != ERROR)) then E1.trans = BOOL else E1.trans = ERROR E -> true E.trans = BOOL E -> false E.trans = BOOL E -> int E.trans = INT E -> ( E ) E1.trans = E2.trans Example 2 (cont) Input: (2 + 2) == 4 1. -

Parallel Backtracking with Answer Memoing for Independent And-Parallelism∗
Under consideration for publication in Theory and Practice of Logic Programming 1 Parallel Backtracking with Answer Memoing for Independent And-Parallelism∗ Pablo Chico de Guzman,´ 1 Amadeo Casas,2 Manuel Carro,1;3 and Manuel V. Hermenegildo1;3 1 School of Computer Science, Univ. Politecnica´ de Madrid, Spain. (e-mail: [email protected], fmcarro,[email protected]) 2 Samsung Research, USA. (e-mail: [email protected]) 3 IMDEA Software Institute, Spain. (e-mail: fmanuel.carro,[email protected]) Abstract Goal-level Independent and-parallelism (IAP) is exploited by scheduling for simultaneous execution two or more goals which will not interfere with each other at run time. This can be done safely even if such goals can produce multiple answers. The most successful IAP implementations to date have used recomputation of answers and sequentially ordered backtracking. While in principle simplifying the implementation, recomputation can be very inefficient if the granularity of the parallel goals is large enough and they produce several answers, while sequentially ordered backtracking limits parallelism. And, despite the expected simplification, the implementation of the classic schemes has proved to involve complex engineering, with the consequent difficulty for system maintenance and extension, while still frequently running into the well-known trapped goal and garbage slot problems. This work presents an alternative parallel backtracking model for IAP and its implementation. The model fea- tures parallel out-of-order (i.e., non-chronological) backtracking and relies on answer memoization to reuse and combine answers. We show that this approach can bring significant performance advantages. Also, it can bring some simplification to the important engineering task involved in implementing the backtracking mechanism of previous approaches. -

An Efficient Implementation of the Head-Corner Parser
An Efficient Implementation of the Head-Corner Parser Gertjan van Noord" Rijksuniversiteit Groningen This paper describes an efficient and robust implementation of a bidirectional, head-driven parser for constraint-based grammars. This parser is developed for the OVIS system: a Dutch spoken dialogue system in which information about public transport can be obtained by telephone. After a review of the motivation for head-driven parsing strategies, and head-corner parsing in particular, a nondeterministic version of the head-corner parser is presented. A memorization technique is applied to obtain a fast parser. A goal-weakening technique is introduced, which greatly improves average case efficiency, both in terms of speed and space requirements. I argue in favor of such a memorization strategy with goal-weakening in comparison with ordinary chart parsers because such a strategy can be applied selectively and therefore enormously reduces the space requirements of the parser, while no practical loss in time-efficiency is observed. On the contrary, experiments are described in which head-corner and left-corner parsers imple- mented with selective memorization and goal weakening outperform "standard" chart parsers. The experiments include the grammar of the OV/S system and the Alvey NL Tools grammar. Head-corner parsing is a mix of bottom-up and top-down processing. Certain approaches to robust parsing require purely bottom-up processing. Therefore, it seems that head-corner parsing is unsuitable for such robust parsing techniques. However, it is shown how underspecification (which arises very naturally in a logic programming environment) can be used in the head-corner parser to allow such robust parsing techniques. -

Derivatives of Parsing Expression Grammars
Derivatives of Parsing Expression Grammars Aaron Moss Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, Canada [email protected] This paper introduces a new derivative parsing algorithm for recognition of parsing expression gram- mars. Derivative parsing is shown to have a polynomial worst-case time bound, an improvement on the exponential bound of the recursive descent algorithm. This work also introduces asymptotic analysis based on inputs with a constant bound on both grammar nesting depth and number of back- tracking choices; derivative and recursive descent parsing are shown to run in linear time and constant space on this useful class of inputs, with both the theoretical bounds and the reasonability of the in- put class validated empirically. This common-case constant memory usage of derivative parsing is an improvement on the linear space required by the packrat algorithm. 1 Introduction Parsing expression grammars (PEGs) are a parsing formalism introduced by Ford [6]. Any LR(k) lan- guage can be represented as a PEG [7], but there are some non-context-free languages that may also be represented as PEGs (e.g. anbncn [7]). Unlike context-free grammars (CFGs), PEGs are unambiguous, admitting no more than one parse tree for any grammar and input. PEGs are a formalization of recursive descent parsers allowing limited backtracking and infinite lookahead; a string in the language of a PEG can be recognized in exponential time and linear space using a recursive descent algorithm, or linear time and space using the memoized packrat algorithm [6]. PEGs are formally defined and these algo- rithms outlined in Section 3. -

Unfold/Fold Transformations and Loop Optimization of Logic Programs
Unfold/Fold Transformations and Loop Optimization of Logic Programs Saumya K. Debray Department of Computer Science The University of Arizona Tucson, AZ 85721 Abstract: Programs typically spend much of their execution time in loops. This makes the generation of ef®cient code for loops essential for good performance. Loop optimization of logic programming languages is complicated by the fact that such languages lack the iterative constructs of traditional languages, and instead use recursion to express loops. In this paper, we examine the application of unfold/fold transformations to three kinds of loop optimization for logic programming languages: recur- sion removal, loop fusion and code motion out of loops. We describe simple unfold/fold transformation sequences for these optimizations that can be automated relatively easily. In the process, we show that the properties of uni®cation and logical variables can sometimes be used to generalize, from traditional languages, the conditions under which these optimizations may be carried out. Our experience suggests that such source-level transformations may be used as an effective tool for the optimization of logic pro- grams. 1. Introduction The focus of this paper is on the static optimization of logic programs. Speci®cally, we investigate loop optimization of logic programs. Since programs typically spend most of their time in loops, the generation of ef®cient code for loops is essential for good performance. In the context of logic programming languages, the situation is complicated by the fact that iterative constructs, such as for or while, are unavailable. Loops are usually expressed using recursive procedures, and loop optimizations have be considered within the general framework of inter- procedural optimization. -

Dynamic Programming Via Static Incrementalization 1 Introduction
Dynamic Programming via Static Incrementalization Yanhong A. Liu and Scott D. Stoller Abstract Dynamic programming is an imp ortant algorithm design technique. It is used for solving problems whose solutions involve recursively solving subproblems that share subsubproblems. While a straightforward recursive program solves common subsubproblems rep eatedly and of- ten takes exp onential time, a dynamic programming algorithm solves every subsubproblem just once, saves the result, reuses it when the subsubproblem is encountered again, and takes p oly- nomial time. This pap er describ es a systematic metho d for transforming programs written as straightforward recursions into programs that use dynamic programming. The metho d extends the original program to cache all p ossibly computed values, incrementalizes the extended pro- gram with resp ect to an input increment to use and maintain all cached results, prunes out cached results that are not used in the incremental computation, and uses the resulting in- cremental program to form an optimized new program. Incrementalization statically exploits semantics of b oth control structures and data structures and maintains as invariants equalities characterizing cached results. The principle underlying incrementalization is general for achiev- ing drastic program sp eedups. Compared with previous metho ds that p erform memoization or tabulation, the metho d based on incrementalization is more powerful and systematic. It has b een implemented and applied to numerous problems and succeeded on all of them. 1 Intro duction Dynamic programming is an imp ortant technique for designing ecient algorithms [2, 44 , 13 ]. It is used for problems whose solutions involve recursively solving subproblems that overlap. -

A Right-To-Left Type System for Value Recursion
1 A right-to-left type system for value recursion 61 2 62 3 63 4 Alban Reynaud Gabriel Scherer Jeremy Yallop 64 5 ENS Lyon, France INRIA, France University of Cambridge, UK 65 6 66 1 Introduction Seeking to address these problems, we designed and imple- 7 67 mented a new check for recursive definition safety based ona 8 In OCaml recursive functions are defined using the let rec opera- 68 novel static analysis, formulated as a simple type system (which we 9 tor, as in the following definition of factorial: 69 have proved sound with respect to an existing operational seman- 10 let rec fac x = if x = 0 then 1 70 tics [Nordlander et al. 2008]), and implemented as part of OCaml’s 11 else x * (fac (x - 1)) 71 type-checking phase. Our check was merged into the OCaml distri- 12 Beside functions, let rec can define recursive values, such as 72 bution in August 2018. 13 an infinite list ones where every element is 1: 73 Moving the check from the middle end to the type checker re- 14 74 let rec ones = 1 :: ones stores the desirable property that compilation of well-typed programs 15 75 Note that this “infinite” list is actually cyclic, and consists of asingle does not go wrong. This property is convenient for tools that reuse 16 76 cons-cell referencing itself. OCaml’s type-checker without performing compilation, such as 17 77 However, not all recursive definitions can be computed. The MetaOCaml [Kiselyov 2014] (which type-checks quoted code) and 18 78 following definition is justly rejected by the compiler: Merlin [Bour et al. -

Modular Logic Grammars
MODULAR LOGIC GRAMMARS Michael C. McCord IBM Thomas J. Watson Research Center P. O. Box 218 Yorktown Heights, NY 10598 ABSTRACT scoping of quantifiers (and more generally focalizers, McCord, 1981) when the building of log- This report describes a logic grammar formalism, ical forms is too closely bonded to syntax. Another Modular Logic Grammars, exhibiting a high degree disadvantage is just a general result of lack of of modularity between syntax and semantics. There modularity: it can be harder to develop and un- is a syntax rule compiler (compiling into Prolog) derstand syntax rules when too much is going on in which takes care of the building of analysis them. structures and the interface to a clearly separated semantic interpretation component dealing with The logic grammars described in McCord (1982, scoping and the construction of logical forms. The 1981) were three-pass systems, where one of the main whole system can work in either a one-pass mode or points of the modularity was a good treatment of a two-pass mode. [n the one-pass mode, logical scoping. The first pass was the syntactic compo- forms are built directly during parsing through nent, written as a definite clause grammar, where interleaved calls to semantics, added automatically syntactic structures were explicitly built up in by the rule compiler. [n the two-pass mode, syn- the arguments of the non-terminals. Word sense tactic analysis trees are built automatically in selection and slot-filling were done in this first the first pass, and then given to the (one-pass) pass, so that the output analysis trees were actu- semantic component. -

Adaptive LL(*) Parsing: the Power of Dynamic Analysis
Adaptive LL(*) Parsing: The Power of Dynamic Analysis Terence Parr Sam Harwell Kathleen Fisher University of San Francisco University of Texas at Austin Tufts University [email protected] [email protected] kfi[email protected] Abstract PEGs are unambiguous by definition but have a quirk where Despite the advances made by modern parsing strategies such rule A ! a j ab (meaning “A matches either a or ab”) can never as PEG, LL(*), GLR, and GLL, parsing is not a solved prob- match ab since PEGs choose the first alternative that matches lem. Existing approaches suffer from a number of weaknesses, a prefix of the remaining input. Nested backtracking makes de- including difficulties supporting side-effecting embedded ac- bugging PEGs difficult. tions, slow and/or unpredictable performance, and counter- Second, side-effecting programmer-supplied actions (muta- intuitive matching strategies. This paper introduces the ALL(*) tors) like print statements should be avoided in any strategy that parsing strategy that combines the simplicity, efficiency, and continuously speculates (PEG) or supports multiple interpreta- predictability of conventional top-down LL(k) parsers with the tions of the input (GLL and GLR) because such actions may power of a GLR-like mechanism to make parsing decisions. never really take place [17]. (Though DParser [24] supports The critical innovation is to move grammar analysis to parse- “final” actions when the programmer is certain a reduction is time, which lets ALL(*) handle any non-left-recursive context- part of an unambiguous final parse.) Without side effects, ac- free grammar. ALL(*) is O(n4) in theory but consistently per- tions must buffer data for all interpretations in immutable data forms linearly on grammars used in practice, outperforming structures or provide undo actions. -

Parsing 1. Grammars and Parsing 2. Top-Down and Bottom-Up Parsing 3
Syntax Parsing syntax: from the Greek syntaxis, meaning “setting out together or arrangement.” 1. Grammars and parsing Refers to the way words are arranged together. 2. Top-down and bottom-up parsing Why worry about syntax? 3. Chart parsers • The boy ate the frog. 4. Bottom-up chart parsing • The frog was eaten by the boy. 5. The Earley Algorithm • The frog that the boy ate died. • The boy whom the frog was eaten by died. Slide CS474–1 Slide CS474–2 Grammars and Parsing Need a grammar: a formal specification of the structures allowable in Syntactic Analysis the language. Key ideas: Need a parser: algorithm for assigning syntactic structure to an input • constituency: groups of words may behave as a single unit or phrase sentence. • grammatical relations: refer to the subject, object, indirect Sentence Parse Tree object, etc. Beavis ate the cat. S • subcategorization and dependencies: refer to certain kinds of relations between words and phrases, e.g. want can be followed by an NP VP infinitive, but find and work cannot. NAME V NP All can be modeled by various kinds of grammars that are based on ART N context-free grammars. Beavis ate the cat Slide CS474–3 Slide CS474–4 CFG example CFG’s are also called phrase-structure grammars. CFG’s Equivalent to Backus-Naur Form (BNF). A context free grammar consists of: 1. S → NP VP 5. NAME → Beavis 1. a set of non-terminal symbols N 2. VP → V NP 6. V → ate 2. a set of terminal symbols Σ (disjoint from N) 3. -

Abstract Syntax Trees & Top-Down Parsing
Abstract Syntax Trees & Top-Down Parsing Review of Parsing • Given a language L(G), a parser consumes a sequence of tokens s and produces a parse tree • Issues: – How do we recognize that s ∈ L(G) ? – A parse tree of s describes how s ∈ L(G) – Ambiguity: more than one parse tree (possible interpretation) for some string s – Error: no parse tree for some string s – How do we construct the parse tree? Compiler Design 1 (2011) 2 Abstract Syntax Trees • So far, a parser traces the derivation of a sequence of tokens • The rest of the compiler needs a structural representation of the program • Abstract syntax trees – Like parse trees but ignore some details – Abbreviated as AST Compiler Design 1 (2011) 3 Abstract Syntax Trees (Cont.) • Consider the grammar E → int | ( E ) | E + E • And the string 5 + (2 + 3) • After lexical analysis (a list of tokens) int5 ‘+’ ‘(‘ int2 ‘+’ int3 ‘)’ • During parsing we build a parse tree … Compiler Design 1 (2011) 4 Example of Parse Tree E • Traces the operation of the parser E + E • Captures the nesting structure • But too much info int5 ( E ) – Parentheses – Single-successor nodes + E E int 2 int3 Compiler Design 1 (2011) 5 Example of Abstract Syntax Tree PLUS PLUS 5 2 3 • Also captures the nesting structure • But abstracts from the concrete syntax a more compact and easier to use • An important data structure in a compiler Compiler Design 1 (2011) 6 Semantic Actions • This is what we’ll use to construct ASTs • Each grammar symbol may have attributes – An attribute is a property of a programming language construct