DOCSLIB.ORG

ARITHMETIC: a Textbook for Math 01 3Rd Edition (2012)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ARITHMETIC: a Textbook for Math 01 3Rd Edition (2012) ARITHMETIC: A Textbook for Math 01 3rd edition (2012) Anthony Weaver Department of Mathematics and Computer Science Bronx Community College Page 2 3rd Edition. Copyright c Anthony Weaver, June 2012, Department of Mathematics and Computer ! Science, CPH 315, Bronx Community College, 2155 University Avenue, Bronx, NY 10453. Thanks to the following colleagues for various combinations of proof-reading, technical help, im- provements in pedagogy and/or exposition: Nikos Apostolakis, Luis Fernandez, Marie Hercule, Uma Iyer, Toni Kasper, Alexander Kheyfits, Roman Kossak, George Leibman, Emanuel Paki, Maria Psarelli, Philipp Rothmaler, Camilo Sanabria. Responsibility for errors remains with me. – A.W. June, 2012. Page 3 Page 4 Contents 1 Whole Numbers 9 1.0.1 Exercises . 10 1.1 Adding Whole Numbers . 10 1.1.1 Commutativity, Associativity, Identity . 10 1.1.2 Multi-digit addition . 11 1.1.3 Exercises . 12 1.2 Subtracting Whole Numbers . 14 1.2.1 Commutativity, Associativity, Identity . 15 1.2.2 Multi-digit subtractions . 15 1.2.3 Checking Subtractions . 16 1.2.4 Borrowing . 16 1.2.5 Exercises . 18 1.3 Multiplying Whole Numbers . 20 1.3.1 Commutativity, Associativity, Identity, the Zero Property . 21 1.3.2 Multi-digit multiplications . 21 1.3.3 Exercises . 25 1.4 Powers of Whole Numbers . 26 1.4.1 Squares and Cubes . 27 1.4.2 Exercises . 27 1.4.3 Square Roots . 28 1.4.4 Exercises . 29 1.5 Division of Whole Numbers . 29 1.5.1 Quotient and Remainder . 30 1.5.2 Long Division . 31 1.5.3 Exercises . 35 1.6 Order of operations . 36 1.6.1 Exercises . 38 1.7 Average . 39 1.7.1 Exercises . 39 1.8 Perimeter, Area and the Pythagorean Theorem . 40 1.8.1 Exercises . 47 2 Fractions and Mixed Numbers 49 2.1 What fractions mean . 49 2.2 Proper and Improper Fractions . 50 2.2.1 Zero as Numerator and Denominator . 51 5 2.2.2 Exercises . 52 2.3 Mixed Numbers . 53 2.3.1 Converting an improper fraction into a mixed or whole number . 53 2.3.2 Exercises . 54 2.3.3 Converting a mixed or whole number to an improper fraction . 55 2.3.4 Exercises . 56 2.4 Multiplication of Fractions . 57 2.4.1 Exercises . 59 2.5 Equivalent Fractions . 59 2.5.1 Cancellation and Lowest Terms . 60 2.5.2 Exercises . 62 2.6 Prime Factorization and the GCF . 62 2.6.1 Exercises . 64 2.6.2 Finding the GCF . 64 2.6.3 Exercises . 65 2.6.4 Cancelling the GCF for lowest terms . 65 2.6.5 Exercises . 66 2.7 Pre-cancelling when Multiplying Fractions . 67 2.7.1 Exercises . 69 2.8 Adding and Subtracting Fractions . 69 2.8.1 Exercises . 70 2.8.2 Adding and Subtracting Unlike Fractions . 71 2.8.3 The LCM . 72 2.8.4 Exercises . 73 2.8.5 The LCD . 74 2.8.6 Exercises . 75 2.9 Comparison of Fractions . 76 2.9.1 Exercises . 78 2.10 Division of Fractions . 78 2.10.1 Reciprocals . 78 2.10.2 Exercises . 79 2.10.3 Division is Multiplication by the Reciprocal of the Divisor . 79 2.10.4 Exercises . 81 2.11 Mixed Numbers and Mixed Units . 82 2.11.1 Vertical Addition and Subtraction . 82 2.11.2 Exercises . 84 2.11.3 Measurements in Mixed Units . 85 2.11.4 Exercises . 87 2.12 Combined operations with fractions and mixed numbers . 87 2.12.1 Exercises . 89 3 Decimals and Percents 91 3.1 Decimal place values . 92 3.1.1 Exercises . 93 3.2 Significant and Insignificant 0’s . 93 3.3 Comparing Decimals . 94 3.3.1 Exercises . 95 Page 6 3.4 Rounding-off . 95 3.4.1 Exercises . 97 3.5 Adding and Subtracting Decimals . 97 3.5.1 Exercises . 99 3.6 Multiplying and Dividing Decimals by Powers of 10 . 99 3.6.1 Exercises . 101 3.7 Multiplication of general decimals . 101 3.7.1 Exercises . 102 3.8 Division of a decimal by a whole number . 103 3.8.1 Exercises . 108 3.9 Division of a decimal by a decimal . 108 3.9.1 Exercises . 109 3.10 Percents, Conversions . ..
Load more

Recommended publications
  • Db Math Marco Zennaro Ermanno Pietrosemoli Goals
    dB Math Marco Zennaro Ermanno Pietrosemoli Goals ‣ Electromagnetic waves carry power measured in milliwatts. ‣ Decibels (dB) use a relative logarithmic relationship to reduce multiplication to simple addition. ‣ You can simplify common radio calculations by using dBm instead of mW, and dB to represent variations of power. ‣ It is simpler to solve radio calculations in your head by using dB. 2 Power ‣ Any electromagnetic wave carries energy - we can feel that when we enjoy (or suffer from) the warmth of the sun. The amount of energy received in a certain amount of time is called power. ‣ The electric field is measured in V/m (volts per meter), the power contained within it is proportional to the square of the electric field: 2 P ~ E ‣ The unit of power is the watt (W). For wireless work, the milliwatt (mW) is usually a more convenient unit. 3 Gain and Loss ‣ If the amplitude of an electromagnetic wave increases, its power increases. This increase in power is called a gain. ‣ If the amplitude decreases, its power decreases. This decrease in power is called a loss. ‣ When designing communication links, you try to maximize the gains while minimizing any losses. 4 Intro to dB ‣ Decibels are a relative measurement unit unlike the absolute measurement of milliwatts. ‣ The decibel (dB) is 10 times the decimal logarithm of the ratio between two values of a variable. The calculation of decibels uses a logarithm to allow very large or very small relations to be represented with a conveniently small number. ‣ On the logarithmic scale, the reference cannot be zero because the log of zero does not exist! 5 Why do we use dB? ‣ Power does not fade in a linear manner, but inversely as the square of the distance.
    [Show full text]
  • The Five Fundamental Operations of Mathematics: Addition, Subtraction
    The five fundamental operations of mathematics: addition, subtraction, multiplication, division, and modular forms Kenneth A. Ribet UC Berkeley Trinity University March 31, 2008 Kenneth A. Ribet Five fundamental operations This talk is about counting, and it’s about solving equations. Counting is a very familiar activity in mathematics. Many universities teach sophomore-level courses on discrete mathematics that turn out to be mostly about counting. For example, we ask our students to find the number of different ways of constituting a bag of a dozen lollipops if there are 5 different flavors. (The answer is 1820, I think.) Kenneth A. Ribet Five fundamental operations Solving equations is even more of a flagship activity for mathematicians. At a mathematics conference at Sundance, Robert Redford told a group of my colleagues “I hope you solve all your equations”! The kind of equations that I like to solve are Diophantine equations. Diophantus of Alexandria (third century AD) was Robert Redford’s kind of mathematician. This “father of algebra” focused on the solution to algebraic equations, especially in contexts where the solutions are constrained to be whole numbers or fractions. Kenneth A. Ribet Five fundamental operations Here’s a typical example. Consider the equation y 2 = x3 + 1. In an algebra or high school class, we might graph this equation in the plane; there’s little challenge. But what if we ask for solutions in integers (i.e., whole numbers)? It is relatively easy to discover the solutions (0; ±1), (−1; 0) and (2; ±3), and Diophantus might have asked if there are any more.
    [Show full text]
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
  • James Clerk Maxwell
    James Clerk Maxwell JAMES CLERK MAXWELL Perspectives on his Life and Work Edited by raymond flood mark mccartney and andrew whitaker 3 3 Great Clarendon Street, Oxford, OX2 6DP, United Kingdom Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries c Oxford University Press 2014 The moral rights of the authors have been asserted First Edition published in 2014 Impression: 1 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above You must not circulate this work in any other form and you must impose this same condition on any acquirer Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016, United States of America British Library Cataloguing in Publication Data Data available Library of Congress Control Number: 2013942195 ISBN 978–0–19–966437–5 Printed and bound by CPI Group (UK) Ltd, Croydon, CR0 4YY Links to third party websites are provided by Oxford in good faith and for information only.
    [Show full text]
  • Act Mathematics
    ACT MATHEMATICS Improving College Admission Test Scores Contributing Writers Marie Haisan L. Ramadeen Matthew Miktus David Hoffman ACT is a registered trademark of ACT Inc. Copyright 2004 by Instructivision, Inc., revised 2006, 2009, 2011, 2014 ISBN 973-156749-774-8 Printed in Canada. All rights reserved. No part of the material protected by this copyright may be reproduced in any form or by any means, for commercial or educational use, without permission in writing from the copyright owner. Requests for permission to make copies of any part of the work should be mailed to Copyright Permissions, Instructivision, Inc., P.O. Box 2004, Pine Brook, NJ 07058. Instructivision, Inc., P.O. Box 2004, Pine Brook, NJ 07058 Telephone 973-575-9992 or 888-551-5144; fax 973-575-9134, website: www.instructivision.com ii TABLE OF CONTENTS Introduction iv Glossary of Terms vi Summary of Formulas, Properties, and Laws xvi Practice Test A 1 Practice Test B 16 Practice Test C 33 Pre Algebra Skill Builder One 51 Skill Builder Two 57 Skill Builder Three 65 Elementary Algebra Skill Builder Four 71 Skill Builder Five 77 Skill Builder Six 84 Intermediate Algebra Skill Builder Seven 88 Skill Builder Eight 97 Coordinate Geometry Skill Builder Nine 105 Skill Builder Ten 112 Plane Geometry Skill Builder Eleven 123 Skill Builder Twelve 133 Skill Builder Thirteen 145 Trigonometry Skill Builder Fourteen 158 Answer Forms 165 iii INTRODUCTION The American College Testing Program Glossary: The glossary defines commonly used (ACT) is a comprehensive system of data mathematical expressions and many special and collection, processing, and reporting designed to technical words.
    [Show full text]
  • Number Theory
    “mcs-ftl” — 2010/9/8 — 0:40 — page 81 — #87 4 Number Theory Number theory is the study of the integers. Why anyone would want to study the integers is not immediately obvious. First of all, what’s to know? There’s 0, there’s 1, 2, 3, and so on, and, oh yeah, -1, -2, . Which one don’t you understand? Sec- ond, what practical value is there in it? The mathematician G. H. Hardy expressed pleasure in its impracticality when he wrote: [Number theorists] may be justified in rejoicing that there is one sci- ence, at any rate, and that their own, whose very remoteness from or- dinary human activities should keep it gentle and clean. Hardy was specially concerned that number theory not be used in warfare; he was a pacifist. You may applaud his sentiments, but he got it wrong: Number Theory underlies modern cryptography, which is what makes secure online communication possible. Secure communication is of course crucial in war—which may leave poor Hardy spinning in his grave. It’s also central to online commerce. Every time you buy a book from Amazon, check your grades on WebSIS, or use a PayPal account, you are relying on number theoretic algorithms. Number theory also provides an excellent environment for us to practice and apply the proof techniques that we developed in Chapters 2 and 3. Since we’ll be focusing on properties of the integers, we’ll adopt the default convention in this chapter that variables range over the set of integers, Z. 4.1 Divisibility The nature of number theory emerges as soon as we consider the divides relation a divides b iff ak b for some k: D The notation, a b, is an abbreviation for “a divides b.” If a b, then we also j j say that b is a multiple of a.
    [Show full text]
  • Operations with Algebraic Expressions: Addition and Subtraction of Monomials
    Operations with Algebraic Expressions: Addition and Subtraction of Monomials A monomial is an algebraic expression that consists of one term. Two or more monomials can be added or subtracted only if they are LIKE TERMS. Like terms are terms that have exactly the SAME variables and exponents on those variables. The coefficients on like terms may be different. Example: 7x2y5 and -2x2y5 These are like terms since both terms have the same variables and the same exponents on those variables. 7x2y5 and -2x3y5 These are NOT like terms since the exponents on x are different. Note: the order that the variables are written in does NOT matter. The different variables and the coefficient in a term are multiplied together and the order of multiplication does NOT matter (For example, 2 x 3 gives the same product as 3 x 2). Example: 8a3bc5 is the same term as 8c5a3b. To prove this, evaluate both terms when a = 2, b = 3 and c = 1. 8a3bc5 = 8(2)3(3)(1)5 = 8(8)(3)(1) = 192 8c5a3b = 8(1)5(2)3(3) = 8(1)(8)(3) = 192 As shown, both terms are equal to 192. To add two or more monomials that are like terms, add the coefficients; keep the variables and exponents on the variables the same. To subtract two or more monomials that are like terms, subtract the coefficients; keep the variables and exponents on the variables the same. Addition and Subtraction of Monomials Example 1: Add 9xy2 and −8xy2 9xy2 + (−8xy2) = [9 + (−8)] xy2 Add the coefficients. Keep the variables and exponents = 1xy2 on the variables the same.
    [Show full text]
  • FROM HARMONIC ANALYSIS to ARITHMETIC COMBINATORICS: a BRIEF SURVEY the Purpose of This Note Is to Showcase a Certain Line Of
    FROM HARMONIC ANALYSIS TO ARITHMETIC COMBINATORICS: A BRIEF SURVEY IZABELLA ÃLABA The purpose of this note is to showcase a certain line of research that connects harmonic analysis, speci¯cally restriction theory, to other areas of mathematics such as PDE, geometric measure theory, combinatorics, and number theory. There are many excellent in-depth presentations of the vari- ous areas of research that we will discuss; see e.g., the references below. The emphasis here will be on highlighting the connections between these areas. Our starting point will be restriction theory in harmonic analysis on Eu- clidean spaces. The main theme of restriction theory, in this context, is the connection between the decay at in¯nity of the Fourier transforms of singu- lar measures and the geometric properties of their support, including (but not necessarily limited to) curvature and dimensionality. For example, the Fourier transform of a measure supported on a hypersurface in Rd need not, in general, belong to any Lp with p < 1, but there are positive results if the hypersurface in question is curved. A classic example is the restriction theory for the sphere, where a conjecture due to E. M. Stein asserts that the Fourier transform maps L1(Sd¡1) to Lq(Rd) for all q > 2d=(d¡1). This has been proved in dimension 2 (Fe®erman-Stein, 1970), but remains open oth- erwise, despite the impressive and often groundbreaking work of Bourgain, Wol®, Tao, Christ, and others. We recommend [8] for a thorough survey of restriction theory for the sphere and other curved hypersurfaces. Restriction-type estimates have been immensely useful in PDE theory; in fact, much of the interest in the subject stems from PDE applications.
    [Show full text]
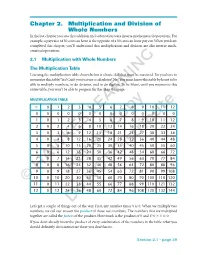
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Pure Mathematics
    Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture.
    [Show full text]
  • From Arithmetic to Algebra
    From arithmetic to algebra Slightly edited version of a presentation at the University of Oregon, Eugene, OR February 20, 2009 H. Wu Why can’t our students achieve introductory algebra? This presentation specifically addresses only introductory alge- bra, which refers roughly to what is called Algebra I in the usual curriculum. Its main focus is on all students’ access to the truly basic part of algebra that an average citizen needs in the high- tech age. The content of the traditional Algebra II course is on the whole more technical and is designed for future STEM students. In place of Algebra II, future non-STEM would benefit more from a mathematics-culture course devoted, for example, to an understanding of probability and data, recently solved famous problems in mathematics, and history of mathematics. At least three reasons for students’ failure: (A) Arithmetic is about computation of specific numbers. Algebra is about what is true in general for all numbers, all whole numbers, all integers, etc. Going from the specific to the general is a giant conceptual leap. Students are not prepared by our curriculum for this leap. (B) They don’t get the foundational skills needed for algebra. (C) They are taught incorrect mathematics in algebra classes. Garbage in, garbage out. These are not independent statements. They are inter-related. Consider (A) and (B): The K–3 school math curriculum is mainly exploratory, and will be ignored in this presentation for simplicity. Grades 5–7 directly prepare students for algebra. Will focus on these grades. Here, abstract mathematics appears in the form of fractions, geometry, and especially negative fractions.
    [Show full text]