Ramji Lal Linear Algebra, Galois Theory, Representation Theory, Group Extensions and Schur Multiplier
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dishant M Pancholi
Dishant M Pancholi Contact Chennai Mathematical Institute Phone: +91 44 67 48 09 59 Information H1 SIPCOT IT Park, Siruseri Fax: +91 44 27 47 02 25 Kelambakkam 603103 E-mail: [email protected] India Research • Contact and symplectic topology Interests Employment Assitant Professor June 2011 - Present Chennai Mathematical Institute, Kelambakkam, India Post doctoral Fellow (January 2008 - January 2010) International Centre for Theoratical physics,Trieste, Italy. Visiting Fellow, (October 2006 - December 2007) TIFR Centre, Bangalore, India. Education School of Mathematics, Tata Institute of Fundamental Research, Mumbai, India. Ph.D, August 1999 - September 2006. Thesis title: Knots, mapping class groups and Kirby calculus. Department of Mathematics, M.S. University of Baroda, Vadodara, India. M.Sc (Mathematics), 1996 - 1998. M.S. University of Baroda, Vadodara, India B.Sc, 1993 - 1996. Awards and • Shree Ranchodlal Chotalal Shah gold medal for scoring highest marks in mathematics Scholarships at M S University of Baroda, Vadodara in M.Sc. (1998) • Research Scholarship at TIFR, Mumbai. (1999) • Best Thesis award TIFR, Mumbai (2007) Research • ( With Siddhartha Gadgil) Publications Homeomorphism and homology of non-orientable surfaces Proceedings of Indian Acad. of Sciences, 115 (2005), no. 3, 251{257. • ( With Siddhartha Gadgil) Non-orientable Thom-Pontryagin construction and Seifert surfaces. Journal of RMS 23 (2008), no. 2, 143{149. • ( With John Etnyre) On generalizing Lutz twists. Journal of the London Mathematical Society (84) 2011, Issue 3, p670{688 Preprints • (With Indranil Biswas and Mahan Mj) Homotopical height. arXiv:1302.0607v1 [math.GT] • (With Roger Casals and Francisco Presas) Almost contact 5{folds are contact. arXiv:1203.2166v3 [math.SG] (2012)(submitted) • (With Roger Casals and Francisco Presas) Contact blow-up. -

Debashish Goswami Jyotishman Bhowmick Quantum Isometry Groups Infosys Science Foundation Series
Infosys Science Foundation Series in Mathematical Sciences Debashish Goswami Jyotishman Bhowmick Quantum Isometry Groups Infosys Science Foundation Series Infosys Science Foundation Series in Mathematical Sciences Series editors Gopal Prasad, University of Michigan, USA Irene Fonseca, Mellon College of Science, USA Editorial Board Chandrasekhar Khare, University of California, USA Mahan Mj, Tata Institute of Fundamental Research, Mumbai, India Manindra Agrawal, Indian Institute of Technology Kanpur, India S.R.S. Varadhan, Courant Institute of Mathematical Sciences, USA Weinan E, Princeton University, USA The Infosys Science Foundation Series in Mathematical Sciences is a sub-series of The Infosys Science Foundation Series. This sub-series focuses on high quality content in the domain of mathematical sciences and various disciplines of mathematics, statistics, bio-mathematics, financial mathematics, applied mathematics, operations research, applies statistics and computer science. All content published in the sub-series are written, edited, or vetted by the laureates or jury members of the Infosys Prize. With the Series, Springer and the Infosys Science Foundation hope to provide readers with monographs, handbooks, professional books and textbooks of the highest academic quality on current topics in relevant disciplines. Literature in this sub-series will appeal to a wide audience of researchers, students, educators, and professionals across mathematics, applied mathematics, statistics and computer science disciplines. More information -

ANNEXURE 1 School of Mathematics Sciences —A Profile As in March 2010
University Yearbook (Academic Audit Report 2005-10) ANNEXURE 1 School of Mathematics Sciences —A Profile as in March 2010 Contents 1. Introduction 1 1.1. Science Education: A synthesis of two paradigms 2 2. Faculty 3 2.1. Mathematics 4 2.2. Physics 12 2.3. Computer Science 18 3. International Links 18 3.1. Collaborations Set Up 18 3.2. Visits by our faculty abroad for research purposes 19 3.3. Visits by faculty abroad to Belur for research purposes 19 4. Service at the National Level 20 4.1. Links at the level of faculty 20 5. Student Placement 21 5.1. 2006-8 MSc Mathematics Batch 21 5.2. 2008-10 MSc Mathematics Batch 22 6. Research 23 1. Introduction Swami Vivekananda envisioned a University at Belur Math, West Bengal, the headquarters of the Ramakrishna Mission. In his conversation with Jamshedji Tata, it was indicated that the spirit of austerity, service and renun- ciation, traditionally associated with monasticism could be united with the quest for Truth and Universality that Science embodies. An inevitable fruit of such a synthesis would be a vigorous pursuit of science as an aspect of Karma Yoga. Truth would be sought by research and the knowledge obtained disseminated through teach- ing, making knowledge universally available. The VivekanandaSchool of Mathematical Sciences at the fledgling Ramakrishna Mission Vivekananda University, headquartered at Belur, has been set up keeping these twin ide- als in mind. We shall first indicate that at the National level, a realization of these objectives would fulfill a deeply felt National need. 1.1. -

LIST of PUBLICATIONS (1) (With S. Ramanan), an Infinitesimal Study of the Moduli of Hitchin Pairs. Journal of the London Mathema
LIST OF PUBLICATIONS INDRANIL BISWAS (1) (With S. Ramanan), An infinitesimal study of the moduli of Hitchin pairs. Journal of the London Mathematical Society, Vol. 49, No. 2, (1994), 219{231. (2) A remark on a deformation theory of Green and Lazarsfeld. Journal f¨urdie Reine und Angewandte Mathematik, Vol. 449 (1994), 103{124. (3) (With N. Raghavendra), Determinants of parabolic bundles on Riemann surfaces. Proceedings of the Indian Academy of Sciences (Math. Sci.), Vol. 103, No. 1, (1993), 41{71. (4) (With K. Guruprasad), Principal bundles on open surfaces and invariant functions on Lie groups. International Journal of Mathematics, Vol. 4, No. 4, (1993), 535{ 544. (5) Secondary invariants of Higgs bundles. International Journal of Mathematics, Vol. 6, No. 2, (1995), 193{204. (6) On the mapping class group action on the cohomology of the representation space of a surface. Proceedings of the American Mathematical Society, Vol. 124, No. 6, (1996), 1959{1965. (7) (With K. Guruprasad), On some geometric invariants associated to the space of flat connections on an open surface. Canadian Mathematical Bulletin, Vol. 39, No. 2, (1996), 169{177. (8) A remark on Hodge cycles on moduli spaces of rank 2 bundles over curves. Journal f¨urdie Reine und Angewandte Mathematik, Vol. 370 (1996), 143{152. (9) On Harder{Narasimhan filtration of the tangent bundle. Communications in Anal- ysis and Geometry, Vol. 3, No. 1, (1995), 1{10. (10) (With N. Raghavendra), Canonical generators of the cohomology of moduli of parabolic bundles on curves. Mathematische Annalen, Vol. 306, No. 1, (1996), 1{14. (11) (With M. -

The Monk Who Is Sold on Geometry: an Interview with Mahan Maharaj
The Monk Who is Sold on Geometry: An Interview with Mahan Maharaj Professor Mahan Mj is a young geometric topologist at Ramakrishna Mission Vivekananda University, who combines an esoteric career as a research mathematician and teacher with that of a monk. He belongs to the monastic order, Ramakrishna Mission, founded in 1897 by Swami Vivekananda, a renowned Hindu philosopher. He is currently a Professor in the Department of Mathematics, Ramakrishna Mission Vivekananda University, whose campus is located just outside Belur Math, the Headquarters of the Mission in Kolkata, India. Mahan Mj was recently awarded the Shanti Swarup Bhatnagar Award in the Mathematical Sciences, India’s topmost national award that recognises scientific contributions made by Indian scientists under the age of 45. Initially reluctant to be interviewed, saying that he believed in the “anonymity that a mathematician’s career affords’’, Mahan Mj graciously relented and spoke to Sujatha Ramdorai. Sujatha Ramdorai (SR): Please tell us a little about your background and early education. Mahan Mj (MM): My early schooling was at St Xavier’s College, Kolkata and then I did an Integrated MSc (Maths) degree at IIT Kanpur. SR: When did it become clear to you that a career in Mathematics was what you preferred? MM: It’s the subject I liked most at school. Nevertheless, due presumably to social conditioning, I opted to join the BTech programme at IIT Kanpur in Electrical Engineering for the “security” it would provide. This was, however, with the intention of switching to Maths after the BTech. I expressed the intention of returning to Kolkata and joining ISI (Indian Statistical Institute) Kolkata BStat, a few months into the programme as I didn’t quite enjoy Engineering studies. -
![Arxiv:2009.11521V2 [Math.GT] 4 Mar 2021](https://docslib.b-cdn.net/cover/0664/arxiv-2009-11521v2-math-gt-4-mar-2021-2990664.webp)
Arxiv:2009.11521V2 [Math.GT] 4 Mar 2021
PROPAGATING QUASICONVEXITY FROM FIBERS MAHAN MJ AND PRANAB SARDAR π Abstract. Let 1 → K −→ G −→ Q be an exact sequence of hyperbolic −1 groups. Let Q1 < Q be a quasiconvex subgroup and let G1 = π (Q1). Under relatively mild conditions (e.g. if K is a closed surface group or a free group and Q is convex cocompact), we show that infinite index quasiconvex subgroups of G1 are quasiconvex in G. Related results are proven for metric bundles, developable complexes of groups and graphs of groups. 1. Introduction The aim of this paper is to provide evidence in favor of the following Scholium. Scholium 1.1. For an exact sequence π 1 → K −→ G −→ Q → 1 of hyperbolic groups, and more generally for hyperbolic metric bundles, quasicon- vexity in fibers propagates to quasiconvexity in subbundles. There are two specific examples in which the exact sequence in Scholium 1.1 has been studied: (1) When K = π1(Σ) is the fundamental group of a closed surface of genus g > 1, and Q < MCG(Σ). Here, the exact sequence comes from the Birman exact sequence π 1 → π1(Σ) −→ MCG(Σ.∗) −→ MCG(Σ) → 1, where MCG(Σ.∗) denotes the mapping class group of Σ equipped with a marked point ∗. (2) When K = Fn is the free group on n generators (n> 2), and Q < Out(Fn). Here, the exact sequence comes from the Birman exact sequence for free arXiv:2009.11521v2 [math.GT] 4 Mar 2021 groups π 1 → Fn −→ Aut(Fn) −→ Out(Fn) → 1. Date: March 5, 2021. 2010 Mathematics Subject Classification. -

B3-I School of Mathematics (Math)
B3-I School of Mathematics (Math) Evaluative Report of Departments (B3) I-Math-1 School of Mathematics 1. Name of the Department : School of Mathematics (Math) 2. Year of establishment : 1945 3. Is the Department part of a School/Faculty of the university? It is an entire School. 4. Names of programmes offered (UG, PG, M.Phil., Ph.D., Integrated Masters; Integrated Ph.D., D. Sc, D. Litt, etc.) 1. Ph.D. 2. Integrated M.Sc.-Ph.D. The minimum eligibility criterion for admission to the Ph.D. programme is a Master's degree in any of Mathematics/Statistics/Science/Technology (M.A. / M.Sc. / M. Math / M. Stat / M.E. / M. Tech.). The minimum eligibility criterion for admission to the Integrated Ph.D. programme is a Bachelor's degree in any of Mathematics/Statistics/Science/Technology (B.A. / B.Sc. / B. Math. / B. Stat. / B.E. / B. Tech.). Students without a Master's degree will generally be admitted to the Integrated Ph.D. program and will obtain an M.Sc. degree along the way subject to the completion of all requirements. Students with a four-year Bachelor's degree may be considered for admission to the Ph.D. Programme. 5. Interdisciplinary programmes and departments involved None 6. Courses in collaboration with other universities, industries, foreign institutions, etc. None TIFR NAAC Self-Study Report 2016 I-Math-2 Evaluative Report of Departments (B3) 7. Details of programmes discontinued, if any, with reasons There are no such programmes. 8. Examination System: Annual/Semester/Trimester/Choice Based Credit System There is an evaluation at the end of each semester course, based on assignments and written examinations, and an annual evaluation of courses based on an interview. -

Chennai Mathematical Institute Annual Report 2011 - 2012 75 76 Chennai Mathematical Institute
Chennai Mathematical Institute Annual Report 2011 - 2012 H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Chennai Mathematical Institute H1, SIPCOT IT Park Padur Post, Siruseri, Tamilnadu 603 103. India. Tel: +91-44-2747 0226, 2747 0227 2747 0228, 2747 0229, +91-44-3298 3441 - 3442 Fax: +91-44-2747 0225 WWW: http://www.cmi.ac.in Design and Printing by: Balan Achchagam, Chennai 600 058 Contents 01. Preface ....................................................................................................................... 5 02. Board of Trustees ..................................................................................................... 8 03. Governing Council ................................................................................................... 9 04. Research Advisory Committee ..............................................................................10 05. Academic Council ...................................................................................................11 06. Boards of Studies ....................................................................................................12 07. Institute Members .................................................................................................13 08. Faculty Profiles .......................................................................................................16 09. Awards ....................................................................................................................26 10. Research Activities -
![Arxiv:1810.11429V2 [Math.GR] 10 Jun 2021 Rjc O 5801-1](https://docslib.b-cdn.net/cover/2235/arxiv-1810-11429v2-math-gr-10-jun-2021-rjc-o-5801-1-4542235.webp)
Arxiv:1810.11429V2 [Math.GR] 10 Jun 2021 Rjc O 5801-1
COMMUTATORS, COMMENSURATORS, AND PSL2 Z p q THOMAS KOBERDA AND MAHAN MJ Abstract. Let H ă PSL2pZq be a finite index normal subgroup which is contained in a principal congruence subgroup, and let ΦpHq‰ H denote a term of the lower central series or the derived series of H. In this paper, we prove that the commensurator of ΦpHq in PSL2pRq is discrete. We thus obtain a natural family of thin subgroups of PSL2pRq whose commensurators are discrete, establishing some cases of a conjecture of Shalom. 1. Introduction The Commensurability Criterion for Arithmeticity due to Margulis [12] [15, 16.3.3] says that among irreducible lattices in semi-simple Lie groups, arithmetic lattices are characterized as those that have dense commensura- tors. During the past decade, Zariski dense discrete subgroups of infinite covolume in semi-simple Lie groups, also known as thin subgroups [17], have gained a lot of attention. Heuristically, thin subgroups should be re- garded as non-arithmetic, even though the essential difference between a thin group and a lattice is that the former has infinite covolume in the ambi- ent Lie group. A question attributed to Shalom makes this heuristic precise in the following way: Question 1.1. [8] Suppose that Γ is a thin subgroup of a semisimple Lie group G. Is the commensurator of Γ discrete? Let X be the symmetric space of non-compact type associated to G and arXiv:1810.11429v2 [math.GR] 10 Jun 2021 X denote its Furstenberg boundary. Question 1.1 has been answered affir- mativelyB in the following cases: Date: June 11, 2021. -
Academic Review
ACADEMIC REVIEW for the period April 2011 { January 2016 Department of Mathematics Indian Institute of Science Bangalore February 08, 2016 Contents 1 About the Department 1 1.1 Institute and Department background ................... 1 1.2 Scientific Staff in the Department ...................... 2 1.2.1 Faculty .................................... 2 1.2.2 UGC Research Scientist ........................... 3 1.2.3 Emeritus Scientists ............................. 3 1.2.4 NMI Distinguished Associate ........................ 3 1.2.5 MO Cell Faculty .............................. 4 1.2.6 INSPIRE Fellows/DST Young Scientists .................. 4 1.2.7 Post Doctoral Fellows/Research Associates ................ 4 1.2.8 Students ................................... 6 1.2.9 Visiting Students .............................. 11 2 Center for Advanced Study 12 2.1 Faculty involved ................................. 12 2.1.1 In the identified thrust area . 12 2.1.2 In other area . 12 3 Major achievements 13 3.1 Teaching ...................................... 13 3.2 Research ...................................... 18 3.2.1 Research Highlights in Thrust area ..................... 18 3.2.2 Research Highlights in other areas ..................... 34 3.2.3 Publications ................................. 44 3.3 Human resource training ........................... 67 3.3.1 The National Mathematics Initiative (NMI) . 67 3.3.2 Mathematical Olympiad ........................... 68 3.3.3 Olympiad training camps .......................... 69 3.3.4 Visiting summer students -
Volume 1. No.1 (2015)
TIFR Alumni Association December 2015 December TAA Newsletter IN THIS ISSUE Editor’s Message From the Patron’s Desk TAA President’s Message Public Lectures Prof. Amit Roy Interviews Awards and Honors TIFR News Contributory Articles Prof. J.N. Goswami Prof. P.C. Agrawal Prof. Jayant Narlikar 1 Editor’s Message Enjoy Reading! We are happy to bring to our TAA mem- bers this year's TAA Newsletter "SAMPARK". The online edition has gained excellent popularity among read- ers since 2008. As in the earlier editions, this year's Newsletter too has public lec- tures by distinguished alumni and their Dr. R. S. Chaughule interviews on their work at TIFR and [email protected] personal life. Ex. Tata Institute of Fund. Research Adjunct Professor Ramnarain Ruia College We are happy to note that the TAA mem- Mumbai bership is increasing due to students' en- rollment. For updates please read our portal TAA- Red.com Happy reading Dr. Sangita Bose [email protected] UM-DAE Center for Excellence in Basic Sciences, (CEBS) Mumbai ---------------------------------------------------- Acknowledgement We thank Mr. Mohan Kakade, TAA Admn. Secretary for his efforts in designing this newsletter. 2 From the Patron’s Desk The TAA has been active in the organi- zation of Public Lectures, interviewing some of the distinguished speakers, recognizing the work of distinguished alumni through TAA Excellence awards and recognizing the students for their exemplary performance in their doc- toral work. The special Cowsik awards have had exceptional works of young scientists being recognized. This year, I am happy to note, that the TAA has introduced the award for Excellence in Teaching, and that four eminent scientists have been chosen in the field of Biology and Physics for this award. -
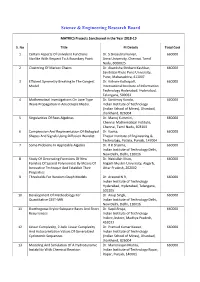
List of MATRICS Projects Funded by SERB During 2018-19
Science & Engineering Research Board MATRICS Projects Sanctioned in the Year 2018-19 S. No Title PI Details Total Cost 1 Certain Aspects Of Univalent Functions Dr. S Sivasubramanian, 660000 Starlike With Respect To A Boundary Point Anna University, Chennai, Tamil Nadu, 6000025 2 Clustering Of Markov Chains Dr. Akanksha Shrikant Kashikar, 660000 Savitribai Phule Pune University, Pune, Maharashtra, 411007 3 Efficient Symmetry Breaking In The Congest Dr. Kishore Kothapalli, 660000 Model International Institute of Information Technology Hyderabad, Hyderabad, Telangana, 500032 4 Mathematical Investigations On Love Type Dr. Santimoy Kundu, 660000 Wave Propagation In Anisotropic Media. Indian Institute of Technology (Indian School of Mines), Dhanbad, Jharkhand, 826004 5 Singularities Of Rees Algebras Dr. Manoj Kummini, 660000 Chennai Mathematical Institute, Chennai, Tamil Nadu, 603103 6 Compression And Representation Of Biological Dr. Kavita, 660000 Shapes And Signals Using Diffusion Wavelet. Thapar Institute of Engineering & Technology, Patiala, Punjab, 147004 7 Some Problems In Applicable Algebra Dr. R K Sharma, 660000 Indian Institute of Technology Delhi, New Delhi, Delhi, 110016 8 Study Of Generating Functions Of New Dr. Nabiullah Khan, 660000 Families Of Special Polynomials By Means Of Aligarh Muslim University, Aligarh, Innovative Technique And Establish Their Uttar Pradesh, 202002 Properties 9 Thresholds For Random Graph Models Dr. Aravind N R, 660000 Indian Institute of Technology Hyderabad, Hyderabad, Telangana, 502205 10 Development Of Methodology For Dr. Anup Singh, 660000 Quantitative CEST-MRI Indian Institute of Technology Delhi, New Delhi, Delhi, 110016 11 Biorthogonal Krylov Subspace Bases And Short Dr. Kapil Ahuja, 660000 Recurrences Indian Institute of Technology Indore, Indore, Madhya Pradesh, 452011 12 Linear Complexity, 2-Adic Linear Complexity Dr.