Options and Futures: a Tutorial
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Up to EUR 3,500,000.00 7% Fixed Rate Bonds Due 6 April 2026 ISIN
Up to EUR 3,500,000.00 7% Fixed Rate Bonds due 6 April 2026 ISIN IT0005440976 Terms and Conditions Executed by EPizza S.p.A. 4126-6190-7500.7 This Terms and Conditions are dated 6 April 2021. EPizza S.p.A., a company limited by shares incorporated in Italy as a società per azioni, whose registered office is at Piazza Castello n. 19, 20123 Milan, Italy, enrolled with the companies’ register of Milan-Monza-Brianza- Lodi under No. and fiscal code No. 08950850969, VAT No. 08950850969 (the “Issuer”). *** The issue of up to EUR 3,500,000.00 (three million and five hundred thousand /00) 7% (seven per cent.) fixed rate bonds due 6 April 2026 (the “Bonds”) was authorised by the Board of Directors of the Issuer, by exercising the powers conferred to it by the Articles (as defined below), through a resolution passed on 26 March 2021. The Bonds shall be issued and held subject to and with the benefit of the provisions of this Terms and Conditions. All such provisions shall be binding on the Issuer, the Bondholders (and their successors in title) and all Persons claiming through or under them and shall endure for the benefit of the Bondholders (and their successors in title). The Bondholders (and their successors in title) are deemed to have notice of all the provisions of this Terms and Conditions and the Articles. Copies of each of the Articles and this Terms and Conditions are available for inspection during normal business hours at the registered office for the time being of the Issuer being, as at the date of this Terms and Conditions, at Piazza Castello n. -

Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces
DEGREE PROJECT IN MATHEMATICS, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2020 Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ENGINEERING SCIENCES Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON Degree Projects in Mathematical Statistics (30 ECTS credits) Master's Programme in Applied and Computational Mathematics (120 credits) KTH Royal Institute of Technology year 2020 Supervisor at Nasdaq Technology AB: Sebastian Lindberg Supervisor at KTH: Fredrik Viklund Examiner at KTH: Fredrik Viklund TRITA-SCI-GRU 2020:081 MAT-E 2020:044 Royal Institute of Technology School of Engineering Sciences KTH SCI SE-100 44 Stockholm, Sweden URL: www.kth.se/sci Abstract The implied volatility surface plays an important role for Front office and Risk Manage- ment functions at Nasdaq and other financial institutions which require mark-to-market of derivative books intraday in order to properly value their instruments and measure risk in trading activities. Based on the aforementioned business needs, being able to calibrate an end of day implied volatility surface based on new market information is a sought after trait. In this thesis a statistical learning approach is used to calibrate the implied volatility surface intraday. This is done by using OMXS30-2019 implied volatil- ity surface data in combination with market information from close to at the money options and feeding it into 3 Machine Learning models. The models, including Feed For- ward Neural Network, Recurrent Neural Network and Gaussian Process, were compared based on optimal input and data preprocessing steps. -

Tracking and Trading Volatility 155
ffirs.qxd 9/12/06 2:37 PM Page i The Index Trading Course Workbook www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page ii Founded in 1807, John Wiley & Sons is the oldest independent publishing company in the United States. With offices in North America, Europe, Aus- tralia, and Asia, Wiley is globally committed to developing and marketing print and electronic products and services for our customers’ professional and personal knowledge and understanding. The Wiley Trading series features books by traders who have survived the market’s ever changing temperament and have prospered—some by reinventing systems, others by getting back to basics. Whether a novice trader, professional, or somewhere in-between, these books will provide the advice and strategies needed to prosper today and well into the future. For a list of available titles, visit our web site at www.WileyFinance.com. www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page iii The Index Trading Course Workbook Step-by-Step Exercises and Tests to Help You Master The Index Trading Course GEORGE A. FONTANILLS TOM GENTILE John Wiley & Sons, Inc. www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page iv Copyright © 2006 by George A. Fontanills, Tom Gentile, and Richard Cawood. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copyright.com. -

(NSE), India, Using Box Spread Arbitrage Strategy
Gadjah Mada International Journal of Business - September-December, Vol. 15, No. 3, 2013 Gadjah Mada International Journal of Business Vol. 15, No. 3 (September - December 2013): 269 - 285 Efficiency of S&P CNX Nifty Index Option of the National Stock Exchange (NSE), India, using Box Spread Arbitrage Strategy G. P. Girish,a and Nikhil Rastogib a IBS Hyderabad, ICFAI Foundation For Higher Education (IFHE) University, Andhra Pradesh, India b Institute of Management Technology (IMT) Hyderabad, India Abstract: Box spread is a trading strategy in which one simultaneously buys and sells options having the same underlying asset and time to expiration, but different exercise prices. This study examined the effi- ciency of European style S&P CNX Nifty Index options of National Stock Exchange, (NSE) India by making use of high-frequency data on put and call options written on Nifty (Time-stamped transactions data) for the time period between 1st January 2002 and 31st December 2005 using box-spread arbitrage strategy. The advantages of box-spreads include reduced joint hypothesis problem since there is no consideration of pricing model or market equilibrium, no consideration of inter-market non-synchronicity since trading box spreads involve only one market, computational simplicity with less chances of mis- specification error, estimation error and the fact that buying and selling box spreads more or less repli- cates risk-free lending and borrowing. One thousand three hundreds and fifty eight exercisable box- spreads were found for the time period considered of which 78 Box spreads were found to be profit- able after incorporating transaction costs (32 profitable box spreads were identified for the year 2002, 19 in 2003, 14 in 2004 and 13 in 2005) The results of our study suggest that internal option market efficiency has improved over the years for S&P CNX Nifty Index options of NSE India. -

Differences Between Financial Options and Real Options
Lecture Notes in Management Science (2012) Vol. 4: 169–178 4th International Conference on Applied Operational Research, Proceedings © Tadbir Operational Research Group Ltd. All rights reserved. www.tadbir.ca ISSN 2008-0050 (Print), ISSN 1927-0097 (Online) Differences between financial options and real options Tero Haahtela Aalto University, BIT Research Centre, Helsinki, Finland [email protected] Abstract. Real option valuation is often presented to be analogous with financial options valuation. The majority of research on real options, especially classic papers, are closely connected to financial option valuation. They share most of the same assumption about contingent claims analysis and apply close form solutions for partial difference equations. However, many real-world investments have several qualities that make use of the classical approach difficult. This paper presents many of the differences that exist between the financial and real options. Whereas some of the differences are theoretical and academic by nature, some are significant from a practical perspective. As a result of these differences, the present paper suggests that numerical methods and models based on calculus and simulation may be more intuitive and robust methods with looser assumptions for practical valuation. New methods and approaches are still required if the real option valuation is to gain popularity outside academia among practitioners and decision makers. Keywords: real options; financial options; investment under uncertainty, valuation Introduction Differences between real and financial options Real option valuation is often presented to be significantly analogous with financial options valuation. The analogy is often presented in a table format that links the Black and Scholes (1973) option valuation parameters to the real option valuation parameters. -

Are Defensive Stocks Expensive? a Closer Look at Value Spreads
Are Defensive Stocks Expensive? A Closer Look at Value Spreads Antti Ilmanen, Ph.D. November 2015 Principal For several years, many investors have been concerned about the apparent rich valuation of Lars N. Nielsen defensive stocks. We analyze the prices of these Principal stocks using value spreads and find that they are not particularly expensive today. Swati Chandra, CFA Vice President Moreover, valuations may have limited efficacy in predicting strategy returns. This piece lends insight into possible reasons by focusing on the contemporaneous relation (i.e., how changes in value spreads are related to returns over the same period). We highlight a puzzling case where a defensive long/short strategy performed well during a recent two- year period when its value spread normalized from abnormally rich levels. For most asset classes, cheapening valuations coincide with poor performance. However, this relationship turns out to be weaker for long/short factor portfolios where several mechanisms can loosen the presumed strong link between value spread changes and strategy returns. Such wedges include changing fundamentals, evolving positions, carry and beta mismatches. Overall, investors should be cognizant of the tenuous link between value spreads and returns. We thank Gregor Andrade, Cliff Asness, Jordan Brooks, Andrea Frazzini, Jacques Friedman, Jeremy Getson, Ronen Israel, Sarah Jiang, David Kabiller, Michael Katz, AQR Capital Management, LLC Hoon Kim, John Liew, Thomas Maloney, Lasse Pedersen, Lukasz Pomorski, Scott Two Greenwich Plaza Richardson, Rodney Sullivan, Ashwin Thapar and David Zhang for helpful discussions Greenwich, CT 06830 and comments. p: +1.203.742.3600 f: +1.203.742.3100 w: aqr.com Are Defensive Stocks Expensive? A Closer Look at Value Spreads 1 Introduction puzzling result — buying a rich investment, seeing it cheapen, and yet making money — in Are defensive stocks expensive? Yes, mildly, more detail below. -

Risk Management Strategies for Cattlemen
RISK MANAGEMENT STRATEGIES FOR CATTLEMEN Kurtis Ward – President/CEO www.kisokc.com As a former agricultural loan officer, I witnessed first-hand the effects that the Dairy Herd Buyout Program had on the Cattle Market of 1986. During this time, I became intrigued by cattlemen who used some form of risk management (Futures, Options, Forward Contracting, etc.) as compared to those who did nothing but speculate on the cash market. It didn’t take long to observe which group made better financial and marketing decisions (perhaps that “hedging stuff” that my college professors were teaching was really important after all). This market event caused my loan officer career to be transformed into a new profession as a commodity futures broker who specialized in risk management strategies for cattlemen. However, my naïve belief back then was that everyone else was having this “illumination” about cattle hedging at the same time. In the 1980’s, it was said that less than 5% of cattlemen were involved in risk management. Fifteen years later, things haven’t changed much which is quite surprising when you look at the total dollars now at risk in any cattle operation. After what we’ve seen during the cattle market of the past two years, I truly believe that cattlemen cannot afford to be just cattlemen any longer. Rather, they must first be “businessmen” who incidentally invest their, time, money and livelihood in a cattle operation. Therefore, the purpose of this article is to quickly review the basics of several risk management strategies in a way that is very simplistic so that the foundational hedging precepts can be easily understood. -

Valuation of Stock Options
VALUATION OF STOCK OPTIONS The right to buy or sell a given security at a specified time in the future is an option. Options are “derivatives’, i.e. they derive their value from the security that is to be traded in accordance with the option. Determining the value of publicly traded stock options is not a problem as the market sets the price. The value of a non-publicly traded option, however, depends on a number of factors: the price of the underlying security at the time of valuation, the time to exercise the option, the volatility of the underlying security, the risk free interest rate, the dividend rate, and the strike price. In addition to these financial variables, subjective variables also play a role. For example, in the case of employee stock options, the employee and the employer have different reasons for valuation, and, therefore, differing needs result in a different valuation for each party. This appendix discusses the reasons for the valuation of non-publicly traded options, explores and compares the two predominant valuation models, and attempts to identify the appropriate valuation methods for a variety of situations. We do not attempt to explain option-pricing theory in depth nor do we attempt mathematical proofs of the models. We focus on the practical aspects of option valuation, directing the reader to the location of computer calculators and sources of the data needed to enter into those calculators. Why Value? The need for valuation arises in a variety of circumstances. In the valuation of a business, for example, options owned by that business must be valued like any other investment asset. -

Users/Robertjfrey/Documents/Work
AMS 511.01 - Foundations Class 11A Robert J. Frey Research Professor Stony Brook University, Applied Mathematics and Statistics [email protected] http://www.ams.sunysb.edu/~frey/ In this lecture we will cover the pricing and use of derivative securities, covering Chapters 10 and 12 in Luenberger’s text. April, 2007 1. The Binomial Option Pricing Model 1.1 – General Single Step Solution The geometric binomial model has many advantages. First, over a reasonable number of steps it represents a surprisingly realistic model of price dynamics. Second, the state price equations at each step can be expressed in a form indpendent of S(t) and those equations are simple enough to solve in closed form. 1+r D-1 u 1 1 + r D 1 + r D y y ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = u fl u = 1+r D u-1 u 1+r-u 1 u 1 u yd yd ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+r D ÅÅÅÅÅÅÅÅ1 uêÅÅÅÅ-ÅÅÅÅu ÅÅ H L H ê L i y As we will see shortlyH weL Hwill solveL the general problemj by solving a zsequence of single step problems on the lattice. That K O K O K O K O j H L H ê L z sequence solutions can be efficientlyê computed because wej only have to zsolve for the state prices once. k { 1.2 – Valuing an Option with One Period to Expiration Let the current value of a stock be S(t) = 105 and let there be a call option with unknown price C(t) on the stock with a strike price of 100 that expires the next three month period. -

Energy-Related Commodity Futures
Universit¨atUlm Institut f¨urFinanzmathematik Energy-Related Commodity Futures Statistics, Models and Derivatives Dissertation zur Erlangung des Doktorgrades Dr. rer. nat. der Fakult¨at f¨urMathematik und Wirtschaftswissenschaften an der Universit¨at Ulm RSITÄT V E U I L N M U · · S O C I D E N N A D R O U · C · D O O C D E N vorgelegt von Dipl.-Math. oec. Reik H. B¨orger, M. S. Ulm, Juni 2007 ii . iii . Amtierender Dekan: Professor Dr. Frank Stehling 1. Gutachter: Professor Dr. R¨udiger Kiesel, Universit¨at Ulm 2. Gutachter: Professor Dr. Ulrich Rieder, Universit¨atUlm 3. Gutachter: Professor Dr. Ralf Korn, Universit¨at Kaiserslautern Tag der Promotion: 15.10.2007 iv Acknowledgements This thesis would not have been possible without the financial and scientific support by EnBW Trading GmbH. In particular, I received instructive input from Dr. Gero Schindlmayr. He suggested many of the problems that have been covered in this work. In numerous discussions he gave insight into physical and financial details of commodities and commodity markets. I also benefited from his suggestions on aspects of the mathematical models and their applicability to practical questions. I take the opportunity to thank my academic advisor Professor Dr. R¨udiger Kiesel who initiated the collaboration with EnBW from the university’s side and who supported my studies in every possible respect. I highly appreciate his confidence in my work and his encouragement which resulted in an enjoyable working environment that goes far beyond the usual conditions. I thank the members of the Institute of Financial Mathematics at Ulm University, in particular Gregor Mummenhoff, Clemens Prestele and Matthias Scherer, for the many mathematical and non-mathematical activities that enriched my time in Ulm. -
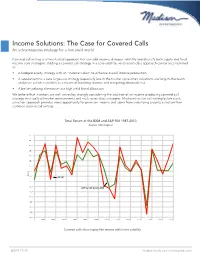
Income Solutions: the Case for Covered Calls an Advantageous Strategy for a Low-Yield World
Income Solutions: The Case for Covered Calls An advantageous strategy for a low-yield world Covered call writing is a time-tested approach that can add income, dampen volatility and diversify both equity and fixed income core strategies. Adding a covered call strategy in a core-satellite, multi-asset-class approach can be accomplished as: • A hedged equity strategy with an “income kicker” to enhance overall income production • A supplement to a core large-cap strategy (especially late in the market cycle when valuations are long-in-the-tooth and price action is volatile) as a means of boosting income and mitigating downside risk • A better-yielding alternative to a high yield bond allocation We believe that investors are well-served by strongly considering the addition of an income-producing covered call strategy in virtually all market environments and multi-asset class strategies. Madison’s active call writing/active stock selection approach provides more opportunity for premium income and alpha from underlying security selection than common passive call writing. Total Return of the BXM and S&P 500 1987-2013 Rolling Returns Source: Morningstar Time Period: 1/1/1987 to 12/31/2013 Rolling Window: 1 Year 1 Year shift 40.0 35.0 30.0 25.0 20.0 15.0 10.0 5.0 Return 0.0 S&P 500 -5.0 -10.0 CBOE S&P 500 Buywrite BXM -15.0 -20.0 -25.0 -30.0 -35.0 -40.0 1989 1991 1993 1995 1997 1999 2001 2003 2005 2007 2009 2011 2013 S&P 500 TR USD Covered calls show equity-likeCBOE returns S&P 500 with Buyw ritelower BXM volatility Source: Morningstar Direct 888.971.7135 madisonfunds.com | madisonadv.com Covered Call Strategy(A) Benefits of Individual Stock Options vs. -

Options Slide Deck Updated Version
www.levelupbootcamps.com 4/4/21 Derivatives Option Strategies 4/4/21 LevelUp, LLC©2021 All rights reserved 1 1 Derivatives & Currency Management Option Strategies 4/4/21 LevelUp, LLC©2021 All rights reserved 2 2 Level Up, LLC©2021 All rights reserved 1 www.levelupbootcamps.com 4/4/21 Risk Management with Options Synthetic Positions • Synthetic Long & Short Forward Option Strategies • Synthetic Puts & Calls Multiple Option Strategies Single Option + Underlying Single Option Directionless Volatility Long U/L Risk Reduction Writing Puts • Long Straddle = LC + LP Covered Call = U/L + SC • Lower purchase cost • Short Straddle = SC + SP • Income enhancement • Fiduciary put = SP + Money Spreads • Reduce at favorable price cash to cover (ftn 13) “Small Moves Up or Down” • Target price realization The Greeks • Bull & Bear Call Spreads • Manza Case 1. Delta + & - • Bear & Bull Put Spreads Protective Put = U/L + LP 2. Gamma + • Insurance Calendar Spreads 3. Theta (time) - Collar = U/L + LP + SC Short “Its all about Theta” 4. Vega (Implied Vol) + • Risk Reversal • Long Calendar Spread Portfolio Mgt • Short Calendar Spread Short U/L Risk Reduction 1. Strategies using • Short U/L + Long Call volatility & market view • Short U/L + Short Put 2. Adjusting risk exposure 4/4/21 LevelUp, LLC©2021 All rights reserved 3 3 Single Option Strategies Refresher . just in case + + X S Long Call – LC S Short Call – SC - - X “writing” Want U/L up – bullish Want U/L down – bearish Right to buy at strike price X Obligated to sell at strike price X Max gain = ∞ when S