Evaluation of Forest Fire Models on a Large Observation Database
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DEFILÉ DES STRETTE ET COLLINES CALCAIRES DE SAINT-FLORENT (Identifiant National : 940013101)
Date d'édition : 20/01/2020 https://inpn.mnhn.fr/zone/znieff/940013101 DEFILÉ DES STRETTE ET COLLINES CALCAIRES DE SAINT-FLORENT (Identifiant national : 940013101) (ZNIEFF Continentale de type 1) (Identifiant régional : 2BSTFLO1) La citation de référence de cette fiche doit se faire comme suite : Piazza C. (Flore 2B), Paradis G. (ASTERE), .- 940013101, DEFILÉ DES STRETTE ET COLLINES CALCAIRES DE SAINT- FLORENT. - INPN, SPN-MNHN Paris, 12P. https://inpn.mnhn.fr/zone/znieff/940013101.pdf Région en charge de la zone : Corse Rédacteur(s) :Piazza C. (Flore 2B), Paradis G. (ASTERE) Centroïde calculé : 1173816°-1768115° Dates de validation régionale et nationale Date de premier avis CSRPN : 02/07/2008 Date actuelle d'avis CSRPN : 02/07/2008 Date de première diffusion INPN : 16/01/2020 Date de dernière diffusion INPN : 16/01/2020 1. DESCRIPTION ............................................................................................................................... 2 2. CRITERES D'INTERET DE LA ZONE ........................................................................................... 3 3. CRITERES DE DELIMITATION DE LA ZONE .............................................................................. 4 4. FACTEUR INFLUENCANT L'EVOLUTION DE LA ZONE ............................................................. 4 5. BILAN DES CONNAISSANCES - EFFORTS DES PROSPECTIONS ........................................... 5 6. HABITATS ..................................................................................................................................... -

Cahier Des Charges De L'appellation D'origine Contrôlée Vin De Corse Ou
Publié au BO-AGRI le Cahier des charges de l’appellation d’origine contrôlée « VIN DE CORSE » ou « CORSE » homologué par le décret n° 2011-1084 du 8 septembre 2011, modifié par arrêté du publié au JORF du CHAPITRE Ier I. - Nom de l’appellation Seuls peuvent prétendre à l’appellation d’origine contrôlée « Vin de Corse » ou « Corse », initialement reconnue par le décret du 22 décembre 1972, les vins répondant aux dispositions particulières fixées ci- après. II. - Dénominations géographiques et mentions complémentaires 1°- Le nom de l’appellation d’origine contrôlée peut être suivi de la dénomination géographique « Calvi » pour les vins répondant aux conditions de production fixées pour cette dénomination géographique dans le présent cahier des charges. 2°- Le nom de l’appellation d’origine contrôlée peut être suivi de la dénomination géographique « Coteaux du Cap Corse » pour les vins répondant aux conditions de production fixées pour cette dénomination géographique dans le présent cahier des charges. 3°- Le nom de l’appellation d’origine contrôlée peut être suivi de la dénomination géographique « Figari » pour les vins répondant aux conditions de production fixées pour cette dénomination géographique dans le présent cahier des charges. 4°- Le nom de l’appellation d’origine contrôlée peut être suivi de la dénomination géographique « Porto- Vecchio » pour les vins répondant aux conditions de production fixées pour cette dénomination géographique dans le présent cahier des charges. 5°- Le nom de l’appellation d’origine contrôlée peut être suivi de la dénomination géographique « Sartène » pour les vins répondant aux conditions de production fixées pour cette dénomination géographique dans le présent cahier des charges. -

Some Reflections on Corsican Secret Societies in the Early Nineteenth Century*
P. SAVIGEAR SOME REFLECTIONS ON CORSICAN SECRET SOCIETIES IN THE EARLY NINETEENTH CENTURY* Stendhal, in La Chartreuse de Parme, described a minister of police who "se garde bien de nier la conspiration, au contraire, seul avec le prince, et arme jusqu'aux dents, il visite tous les coins des appartements, regarde sous les lits et, en un mot, se livre a une foule d'actions ridicules dignes d'une vieille femme." Thus it is when conspiracy is in the air, and such fears were not without parallel in the administrations of the European states in years between 1815 and 1848. The European cabinets in this "age of Metternich" were beset by a fear of revolution, international conspiracy, carbonari and illuminati, and a widespread suspicion of subversion. The picture of clandestine organisation whether drawn in Vienna, Paris, Berlin, Rome or Milan, was not vastly different nor entirely fictitious. The period was punctuated with armed revolts, coups, arrests of agitators, and the appearance of secret societies, often republican, dedicated to the overthrow of the existing order. It is not surprising that contem- poraries and indeed some historians of the period exaggerated the links between these phenomena, even to the extent of occasionally suggesting that one principal organisation was at work with a series of national variants creating an international network. Revolt in Piedmont, Naples and Spain was readily conceived to have a connec- tion with attempted coups elsewhere in Europe. Buonarroti, Mazzini, La Cecilia, Victor Cousin, General Lafayette and many others were observed by the police of Europe as they moved about the continent engaged on legitimate business and perhaps on work of a more sub- versive nature. -

DOCOB ZPS Bonifatu
Document d’objectifs Natura 2000 Zone de Protection Spéciale Site FR9412003 Cirque de Bonifatu (commune de Calenzana, Haute-Corse) Vue panoramique en basse vallée de la ZPS FR 9412003 « Cirque de Bonifatu » S. Nucci Seguin S. Nucci Seguin Milieux rupestres (profil granitique de Bonifatu) et milieux forestiers (pinède essentiellement) de la ZPS « Cirque de Bonifatu ». 2 Document d’objectifs Natura 2000 Zone de Protection Spéciale Site FR9412003 Cirque de Bonifatu (commune de Calenzana, Haute-Corse) Remerciements : à l’ensemble des personnes ayant permis la réalisation de ce document d’objectifs et en particulier à Jean-François Seguin, Mady Torre, José Torre, Brigitte Alessandrini, Franck Finelli (Parc Naturel Régional de Corse) et Bernard Recorbet (DREAL) pour avoir partagé leur connaissances du terrain, des enjeux et des espèces ciblées et pour la relecture attentive du document avant présentation au comité de pilotage. Liste des personnes et structures consultées pour la réalisation des diagnostics et la rédaction des propositions de gestion du site Natura 2000 « Cirque de Bonifatu » : Organisme Personne contactée Forme de la réponse consultation DREAL de Corse Bernard Recorbet Rendez-vous, courrier Oui électronique et appel téléphonique Carole Passigny- Courrier électronique Oui Hernandez Parc Naturel Régional de Jean-François Seguin Rendez-vous Oui Corse Mady Torre Rendez-vous, courrier Oui électronique José Torre Rendez-vous Oui Franck Finelli Rendez-vous Oui Brigitte Alessandrini Rendez-vous Oui Jacky Zuccarrelli Rendez-vous Oui -

Charte Paysagère, Architecturale, Urbaine Et
« L’esprit des lieux » repose sur l’émotion générée par des vues grandioses et rapprochées sur des composantes paysagères singulières Le Grand Site en chiffres Des unités paysagères aux ambiances marquées La côte de Nonza Un paysage étroit où la verticalité des reliefs tombe dans la mer Les crêtes de Teghime Un paysage de montagne avec des vues directes et plongeantes sur les deux côtes de la Corse Les coteaux de Patrimonio Une conque aux facettes paysagères multiples portée par le dynamisme de la viticulture La strette de San Angelo Une bande littorale entre paysage balnéaire et relief symbole La plaine et versants du Nebbiu Un paysage périphérique au territoire du Grand Site Cf. atlas des paysages DREAL Corse Des compositions grandioses, puissantes, colorées et rythmées, dignes d’être peintes Un dynamisme économique porté par Photo @Agauthier la viticulture qui structure et organise le paysage Un respect et un équilibre du patrimoine naturel par une présence discrète des hommes Une puissance minérale qui structure le grand paysage et les perspectives La présence discrète d’un petit patrimoine bâti peu à peu réinvesti Une mémoire collective partagée par de nombreux belvédères et points de vue naturellement présents Un territoire qui favorise aussi des filières non viticoles Filière Bovine Filière Caprine Filière Ovine Filière Apicole L’oliveraie en bordure de mer, un charme indéniable Une finesse du patrimoine bâti et des implantations des villages en harmonie avec le socle géomorphologique Poggio d’Oletta Les Villages de Patrimonio -

Chiffres Clés De L'agriculture Corse
Edition 2015 Chiffres clés de l’agriculture corse Bilan de campagne 2014 Exploitations Vigne Nuciola Elevage Prisuttu Animaux Jeunes agriculteurs Emploi Bovins Données économiques Territoire Casgiu Cheptel Clementina Population agricole AOP Alivu Ovins Castagna Kiwi Caprins Mela Fruits d’été Lait Maraîchage Porcins Fruits à coque Apiculture Agrumes Chiffres clés de l’agriculture corse 2014 - 1 Sommaire DONNÉES GÉNÉRALES Les exploitations ............................................4 Les terres agricoles .........................................5 La population agricole et l’emploi..........................6 Les données économiques .................................7 Les données météorologiques..............................8 LES CULTURES Les agrumes et le kiwi......................................9 La châtaigne ...............................................11 Le maraîchage .............................................12 Les fruits d’été.............................................13 Les fruits à coque..........................................14 L’olive.......................................................15 La vigne ....................................................16 Les fourrages ..............................................18 LES ÉLEVAGES L’apiculture.................................................19 L’élevage bovin.............................................21 L’élevage caprin............................................23 L’élevage ovin ..............................................25 L’élevage porcin............................................27 -

17 Décembre 2019 Page 1 CONVENTION QUINQUENNALE 2020-2024 PREAMBULE La Révision De La Charte Du SM/PNRC : D'une Période D
CONVENTION QUINQUENNALE 2020-2024 RELATIVE A LA DEFINITION ET A LA MISE EN ŒUVRE DES ACTIONS DU SYNDICAT MIXTE DU PARC NATUREL REGIONAL DE CORSE - PARCU DI CORSICA SUR SON TERRITOIRE PREAMBULE La révision de la Charte du SM/PNRC : d’une période d’incertitude à une concertation élargie et déterminante : Le classement du Parc Naturel Régional de Corse (PNRC) avait été renouvelé pour 10 ans par décret du 9 juin 1999 sur un territoire de 145 communes, étendu à deux communes supplémentaires par décret du 12 avril 2007. Une première révision de la charte du Parc Naturel Régional de Corse, avait été prescrite par délibération de l’Assemblée de Corse en date du 30 mars 2007. Elle était initialement envisagée sur un périmètre d’étude identique à celui du périmètre classé en Parc naturel régional. Un débat s’est ensuite instauré sur l’opportunité d’étendre ce périmètre, certains élus considérant que la valeur patrimoniale de la Corse justifiait l’inscription de l’ensemble de l’île en Parc naturel régional. Le diagnostic territorial réalisé en 2011 à la demande de la Collectivité Territoriale de Corse (CTC) a permis d’analyser les possibilités d’extensions pertinentes au regard des critères de classement d’un Parc naturel régional, tels qu’ils sont définis par le code de l’environnement. Le classement du Parc a été prolongé par décret du 2 juin 2009 jusqu’au 9 juin 2011. Depuis cette date, le Parc Naturel Régional de Corse n’était plus classé. La révision de la Charte a par la suite été relancée en juillet 2013, selon un processus concerté avec l’Office de l’Environnement de la Corse, la fédération des parcs naturels régionaux de France et en relation étroite avec l’Etat. -

Liste Des Électeurs Sénatoriaux En Haute-Corse
PRÉFECTURE DE LA HAUTE-CORSE ÉLECTIONS SÉNATORIALES du 27 septembre 2020 ********** Liste des électeurs sénatoriaux (dressé en application des dispositions de l'article R. 146 du code électoral) 1 / 49 1 – SÉNATEUR - CASTELLI Joseph 2 – DÉPUTÉS - ACQUAVIVA Jean-Félix - CASTELLANI Michel 3 - CONSEILLERS A L’ASSEMBLÉE DE CORSE - ARMANET Guy - ARRIGHI Véronique - BENEDETTI François - CARLOTTI Pascal - CASANOVA-SERVAS Marie-Hélène - CECCOLI François-Xavier - CESARI Marcel - COGNETTI-TURCHINI Catherine - DELPOUX Jean-Louis - DENSARI Frédérique - GHIONGA Pierre - GIUDICI Francis - GIOVANNINI Fabienne - GRIMALDI Stéphanie - MARIOTTI Marie-Thérèse - MONDOLONI Jean-Martin - MOSCA Paola - NIVAGGIONI Nadine - ORLANDI François - PADOVANI Marie-Hélène - PAOLINI Julien - PARIGI Paulu-Santu - PIERI Marie-Anne - POLI Antoine - PONZEVERA Juliette - POZZO di BORGO Louis - PROSPERI Rosa - SANTUCCI Anne-Laure - SIMEONI Marie - SIMONI Pascale - TALAMONI Jean-Guy - TOMASI Anne - TOMASI Petr’Antone - VANNI Hyacinthe 4 - DÉLÉGUÉS DES CONSEILS MUNICIPAUX -AGHIONE a) Délégué élu - CASANOVA André b) Suppléants - VIELES Francis - BARCELO Daniel - KLEINEIDAM Hervé -AITI a) Délégué élu - ORSONI Gérard b) Suppléants - ANGELI Marius -ALANDO a) Délégué élu - MAMELLI Guy b) Suppléants - IMPERINETTI Jean-Raphaël - POLETTI Cécile - BERNARDI Jean-François Albert -ALBERTACCE a) Délégué élu - ALBERTINI Pierre-François b) Suppléants - SANTINI Pasquin - ALBERTINI Catherine - ZAMBARO Flavia -ALERIA a) Délégués élus - LUCIANI Dominique - TADDEI Laurence - CHEYNET Patrick - HERMÉ -

Pianello Turene Vassete San-Proteo Pianello Presa
Ruisseau à Mur 120 121 178 73 76 419 296 74 464 d'Otmeta-de-Tuda Mur PIANELLO 8 Ordinaire Chemin Rutali 115 VASSETE 186 465 à 192 RavinRavin 185 Mur 343 Mur 164 295 463 346 187 193 6 294 200 Rutali 10 Mur 9 347 122 291 188 4 11 Mur 163 Chemin 292 191 194 298 293 SAN-PROTEO 159 283 Mur 199 275 Mur 162 Ravin 284 290 Mur 274 Le Bévinco 282 285 Mur d'Olmeta-Di-Tuda 286 289 165 273 189 Mur 276 281 SAN-VITO Mur 204 466 195 203 Ravin 158 345 271 280 Chemin 265 272 198 297 277 288 287 202 161 160 5 458 197 de 459 270 205 123 575 279 460 196 577 576 communal 280 Ravin 278 461 Mur 266 258 264 Mur 124 269 241 462 157 267 240 210 283 268 242 243 257 225 447 156 263 259 239 256 260 238 206 262 255 Ravin 245 207 261 237 (Rivière) Ravin Ravin 236 208 Mur 344 244 Service TURENE 234 235 211 12 Ravin 226 224 253 246 230 209 de 155 de 35 233 Mur Mur 127 213 231 254 247 216 212 252 126 RavinRavin 223 581 281 Ruisseau 250 232 279 227 222 251 214 de 34 248 Ruisseau 448 340 228 154 Mur Ruisseau de Castrabaccha215 221 31 153 13 Chemin Chemin 578 33 249 14 229 36 220 218 282 Ruisseau Castrabaccha 128 152 de 32 dede Ruisseau 217 59 Service 219 278 149 148 129 277 64 B Fureno Saint-Andréà 314 Fureno 147 276 Saint-Andréà 151 30 582 Ravin 275 150 66 PIANELLO 1229 61 63 65 67 315 583 communal Mur 62 579 37 Chemin 131 15 58 313 130 PRESA 60 Mur 312 Bastia Ruisseau Ruisseau 134 Ruisseau 250 50 29 Service 146 de 82 83 de PRESA 57 274 68 Ravin 249 132 1230 133 316 145 273 77 TROITA 135 Tezzola GIUNCULA 16 Mur 584 136 580 Mur de Ruisseau 144 Ordinaire 311 38 39 251 84 -

Avis De La Mission Régionale D'autorité Environnementale De
Corse Avis de la Mission Régionale d’Autorité environnementale de Corse sur l’élaboration du plan local d’urbanisme de VICO (Corse-du-Sud) n°MRAe 2018-02 1 AVIS DÉLIBÉRÉ N° 2018-02 adopté lors de la séance du 11 juin 2018 par La mission régionale d’autorité environnementale de Corse Préambule La Mission régionale d’autorité environnementale (MRAe) de Corse s’est réunie téléphoniquement le XXXXX 2018. L’ordre du jour comportait notamment, l’avis sur l’élaboration du plan local d’urbanisme (PLU) de la commune de Vico. Étaient présents et ont délibéré : Fabienne Allag-Dhuisme présidente, Jet en tant que membres associés, Marie Livia Leoni et Louis Olivier ; Etait excusé : Jean-Pierre Viguier, membre permanent titulaire. Était présent sans voix délibérative : Jean-Marie Seité membre associé suppléant. En application de l’article 9 du règlement intérieur du CGEDD, chacun des membres délibérants cités ci- dessus atteste qu’aucun intérêt particulier ou élément dans ses activités passées ou présentes n’est de nature à mettre en cause son impartialité dans l’avis à donner sur le projet qui fait l’objet du présent avis. L’ordonnance n°2004-489 du 3 juin 2004, portant transposition de la directive 2001/42/CE du parlement européen et du Conseil du 27 juin 2001, a introduit la notion d’évaluation des incidences de certains plans et programmes sur l’environnement. Le décret n°2005-608 du 27 mai 2005 a complété le code de l’urbanisme par les articles désormais codifiés R. 104-1 et suivants. La procédure d’évaluation environnementale, diligentée au stade de la planification, en amont des projets opérationnels, vise à repérer de façon préventive les impacts potentiels des grandes orientations du document d’urbanisme sur l’environnement, à un stade où les infléchissements sont plus aisés à mettre en œuvre. -
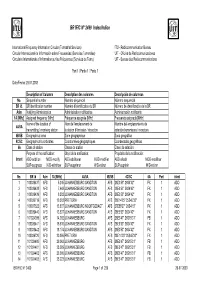
BR IFIC N° 2499 Index/Indice
BR IFIC N° 2499 Index/Indice International Frequency Information Circular (Terrestrial Services) ITU - Radiocommunication Bureau Circular Internacional de Información sobre Frecuencias (Servicios Terrenales) UIT - Oficina de Radiocomunicaciones Circulaire Internationale d'Information sur les Fréquences (Services de Terre) UIT - Bureau des Radiocommunications Part 1 / Partie 1 / Parte 1 Date/Fecha: 29.07.2003 Description of Columns Description des colonnes Descripción de columnas No. Sequential number Numéro séquenciel Número sequencial BR Id. BR identification number Numéro d'identification du BR Número de identificación de la BR Adm Notifying Administration Administration notificatrice Administración notificante 1A [MHz] Assigned frequency [MHz] Fréquence assignée [MHz] Frecuencia asignada [MHz] Name of the location of Nom de l'emplacement de Nombre del emplazamiento de 4A/5A transmitting / receiving station la station d'émission / réception estación transmisora / receptora 4B/5B Geographical area Zone géographique Zona geográfica 4C/5C Geographical coordinates Coordonnées géographiques Coordenadas geográficas 6A Class of station Classe de station Clase de estación Purpose of the notification: Objet de la notification: Propósito de la notificación: Intent ADD-addition MOD-modify ADD-additioner MOD-modifier ADD-añadir MOD-modificar SUP-suppress W/D-withdraw SUP-supprimer W/D-retirer SUP-suprimir W/D-retirar No. BR Id Adm 1A [MHz] 4A/5A 4B/5B 4C/5C 6A Part Intent 1 100039437 AFS 5.245 JOHANNESBURG SANDTON AFS 28E3'53" 26S4'42" FX 1 ADD -

Enquête Sur La Non Restauration De La Chapelle San Tumasgiu Di Pastureccia
Partie 1 Enquête sur la non restauration de la chapelle San Tumasgiu di Pastureccia 1 Présentation 2 Quand je suis dans mon village de Bisinchi, au niveau du chef lieu, je perçois une crête à une altitude semblable d’environ 600 mètres, à moins d’un kilomètre à vol d’oiseau. Elle s’achève par un éperon rocheux qui porte les ruines du château qui dominait les alentours : u Castellu di Rustinu. La crête est couverte de maquis. Si on y prête attention, une bâtisse de taille modeste s’en distingue à sa moitié. Il ne s’agit pas d’un pailler construit dans la pierre locale, du schiste multicolore avec une forte présence de bleu, recouvert de lauzes grisâtres. Non, c’est une chapelle médiévale comme il en existe des dizaines dans l’île. Je quitte Bisinchi pour la rejoindre. Sans croiser aucune voiture, je passe par les hameaux de Vignale, quitte la commune et pénètre dans la commune de Castellu di Rustinu. Sur une étroite route départementale, entre des chênes verts et des châtaigniers parfois centenaires, je prends quelques embranchements avant de me garer au niveau d’un cimetière. Le parking qui comprend quelques places est vide. Une vache broute tranquillement sur un terrain mitoyen. Je pousse la grille, je fais quelques pas. Je me trouve enfin devant la chapelle San Tumasgiu di Pastureccia. Entourée de tombes, sur un site qui ouvre sur une vue panoramique qui plonge sur la vallée du Golu qui 400 mètres plus bas est traversée par le pont génois de Ponte Novu. Le bâtiment est d’une vingtaine de mètres de long.