Surface Waves in Elastic Material
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Acoustic Phonon Scattering from Particles Embedded in an Anisotropic Medium: a Molecular Dynamics Study
University of Pennsylvania ScholarlyCommons Department of Mechanical Engineering & Departmental Papers (MEAM) Applied Mechanics March 2008 Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study Neil Zuckerman University of Pennsylvania Jennifer R. Lukes University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/meam_papers Recommended Citation Zuckerman, Neil and Lukes, Jennifer R., "Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study" (2008). Departmental Papers (MEAM). 145. https://repository.upenn.edu/meam_papers/145 Reprinted from Physical Review B, Volume 77, Article 094302, March 2008, 20 pages. Publisher URL: http://dx.doi.org/10.1103/PhysRevB.77.094302 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/meam_papers/145 For more information, please contact [email protected]. Acoustic phonon scattering from particles embedded in an anisotropic medium: A molecular dynamics study Abstract Acoustic phonon scattering from isolated nanometer-scale impurity particles embedded in anisotropic media is investigated using molecular dynamics simulation. The spectral-directional dependence of the scattering, for both longitudinal and transverse modes, is found through calculation of scattering cross sections and three dimensional scattering phase functions for inclusions of varying sizes, shapes, and stiffnesses and for waves of different wave numbers. The -

Curriculum Overview Physics/Pre-AP 2018-2019 1St Nine Weeks
Curriculum Overview Physics/Pre-AP 2018-2019 1st Nine Weeks RESOURCES: Essential Physics (Ergopedia – online book) Physics Classroom http://www.physicsclassroom.com/ PHET Simulations https://phet.colorado.edu/ ONGOING TEKS: 1A, 1B, 2A, 2B, 2C, 2D, 2F, 2G, 2H, 2I, 2J,3E 1) SAFETY TEKS 1A, 1B Vocabulary Fume hood, fire blanket, fire extinguisher, goggle sanitizer, eye wash, safety shower, impact goggles, chemical safety goggles, fire exit, electrical safety cut off, apron, broken glass container, disposal alert, biological hazard, open flame alert, thermal safety, sharp object safety, fume safety, electrical safety, plant safety, animal safety, radioactive safety, clothing protection safety, fire safety, explosion safety, eye safety, poison safety, chemical safety Key Concepts The student will be able to determine if a situation in the physics lab is a safe practice and what appropriate safety equipment and safety warning signs may be needed in a physics lab. The student will be able to determine the proper disposal or recycling of materials in the physics lab. Essential Questions 1. How are safe practices in school, home or job applied? 2. What are the consequences for not using safety equipment or following safe practices? 2) SCIENCE OF PHYSICS: Glossary, Pages 35, 39 TEKS 2B, 2C Vocabulary Matter, energy, hypothesis, theory, objectivity, reproducibility, experiment, qualitative, quantitative, engineering, technology, science, pseudo-science, non-science Key Concepts The student will know that scientific hypotheses are tentative and testable statements that must be capable of being supported or not supported by observational evidence. The student will know that scientific theories are based on natural and physical phenomena and are capable of being tested by multiple independent researchers. -

Academic Year 2016- 2017 Third Term Science Revision Sheets SCIENCE Name: Date: Grade
Academic Year 2016- 2017 Third Term Science Revision sheets SCIENCE Name: ________________________ Date: _______________ Grade:6 Section: _____________ Q1: Choose the letter of the choice that best answer the questions: 1. How can the speed of a mechanical wave be calculated? A. Add the wavelength and the period. B. Divide the period by the wavelength. C. Divide the wavelength by the period. D. Multiply the wavelength and the period. 2. What is one way that electromagnetic waves differ from mechanical waves? A. Electromagnetic waves move slower. B. Electromagnetic waves are longitudinal. C. Electromagnetic waves can travel through empty space. D. There is no difference between electromagnetic and mechanical waves. 3. What is the name of the lowest point of a wave? A. crest B. trough C. amplitude D. rest position 4. Astronomers study radio waves to learn about the universe. Why might radio waves be used to study objects in space? lesson quiz A. They are sound waves that cause vibrations in stars and planets. B. They are electromagnetic waves, so they don’t require a medium. C. They are mechanical waves that pass through interstellar particles. D. They are longitudinal waves, which create compressions in the fabric of space. 5. Which is the best description of a wave? A. energy that makes particles move B. a disturbance that transfers energy C. a disruption causing the transfer of matter D. any type of matter that vibrates back and forth 6. A wave produced by an earthquake appears in the diagram below: A second wave leaves the center of an earthquake at the same time. -

Chapter 15 Mechanical Waves 1 Types of Mechanical Waves
Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves{waves that travel within some material called a medium. Waves play an important role in how we perceive our physical world (e.g., sight and sound). Not all waves are mechanical, (e.g., electromagnetic waves); however, the terminology and concepts we introduce in this chapter apply to all kinds of waves. A mechanical wave is a disturbance that travels through some material or substance called the medium for the wave. There are basically two kinds of waves{transverse and longitudinal waves. Waves propagate through the medium at a definite speed called the wave speed. As the wave propagates through the medium, the particles sustaining the wave motion move in simple harmonic motion about their equilibrium points. While there is no net transport of matter during the propagation of a wave, there is energy transport from one region to another. 1 2 Periodic Waves As the name implies, these waves occur with a certain repetition that can be de- scribed characteristic properties. A = the amplitude (mm, or m) f = the frequency (Hz) T = the period (s) λ = the wavelength (mm, or m) A special class of periodic waves are harmonic waves. These waves can be described by sine and cosine functions, similar to what we did with simple harmonic motion. For periodic waves, there is a relation between the wavelength and frequency: v = fλ where v is the speed of propagation. 2.1 Transverse Waves Particles in the medium move in a direction perpendicular to the direction of prop- agation. -
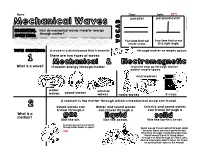
What Is a Wave? Transmit Energy Through Matter
Name: ____________________________________________________________________ Class: ______________ Date: _____________KEY parallel perpendicular How do mechanical waves transfer energy 2018 © Science Sunrise through matter? Two lines that will Two lines that cross never cross. at a right angle. A wave is a disturbance that transmits through matter or empty space. There are two types of waves: What is a wave? Transmit energy through matter. Transmit energy through matter and/or empty space. microwaves water seismic sound waves waves waves radio waves X-rays A medium is the matter through which a mechanical wave can travel. Sound waves can Water and sound waves Seismic and sound waves travel through a can travel through a can travel through a What is a medium? like the air. like the ocean. like the Earth’s crust. Do sound waves travel fastest through solids, liquids, or gases? Sound waves travel fastest through solids solids because there are more particles and they have stronger bonds between them. Sound waves travel 14 times faster through iron than through air! This is why Native Americans used to listen for trains by putting their ears on the tracks! KEY The particles of the medium vibrate in a direction perpendicular What are the to the direction that the main types of Describe the motion of an individual fan wave moves. during ‘The Wave’. How is this an example mechanical of a transverse wave? World Record for Stadium Wave waves and https://tinyurl.com/zn7hr6h Each fan stands up and sits down when ‘The Wave’ energy comes to how do they him/her. The fans are like particles transfer through which energy is transferred, but which do not move. -

1 Phys:1200 Lecture 21 — Vibration, Waves, and Sound
1 PHYS:1200 LECTURE 21 — VIBRATION, WAVES, AND SOUND (2) In the last lecture we discussed oscillating systems which involves the periodic motion of an object like, e.g., a pendulum. However, the system as a whole remains at a fixed location. A wave is an oscillation accompanied by a transfer of energy that travels through space or mass— it is a type of moving oscillation of a medium, or in the case of electromagnetic waves, oscillations of electric and magnetic fields through a vacuum. 21‐1. Waves.—When you toss a pebble into a calm pond, ripples move outward from the point where the pebble enters the water surface. The pebble disturbs the water and wave propagate outward. What we actually see in the rearrangement of the water’s surface is the motion of the disturbance. Some of the energy of the motion of the initial disturbance is transferred outwardly in the water. Notice that the wave (disturbance) moves outward but not the water. When the disturbances reaches a certain position in the water, the water surface rises and falls. Ships moving through the ocean create a disturbance that propagates outward from its sides. A mechanical wave then is a disturbance that propagates through a medium or through space. The water wave is an example of a mechanical wave in which a disturbance moves through a material medium. Another common example of a mechanical wave is a sound wave which is a pressure or density disturbance that propagates through a gas, liquid, or a solid. Mechanical waves must have a medium to propagate the disturbance. -

APS Science Curriculum Unit Planner
APS Science 2011 APS Science Curriculum Unit Planner Grade Level/Subject Physics - Waves Stage 1: Desired Results Enduring Understanding All waves, regardless of origin or type, transmit energy from one place to another and share a common set of characteristics that explain their behavior. Wave behavior can be used to understand and explain many everyday phenomena. Correlations Unifying Understanding VA SOL PH.8 The student will investigate and understand wave phenomena. Key concepts include a) wave characteristics; b) fundamental wave processes; and c) light and sound in terms of wave models. PH.9 The student will investigate and understand that different frequencies and wavelengths in the electromagnetic spectrum are phenomena ranging from radio waves through visible light to gamma radiation. Key concepts include a) the properties, behaviors, and relative size of radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays; b) wave/particle dual nature of light; and c) current applications based on the respective wavelengths. NSES (grade level) Grades 9-12, Standard B essay, pages 177-178 Interactions of Energy and Matter, page 180 AAAS Atlas Waves, Pages 64-65 Essential Questions How do wave characteristics determine their behavior? Knowledge and Skills Students should know: 1 APS Science 2011 •Mechanical waves transport energy as a traveling disturbance in a medium. •In a transverse wave, particles of the medium oscillate in a direction perpendicular to the direction the wave travels. •In a longitudinal wave, particles of the medium oscillate in a direction parallel to the direction the wave travels. •Wave velocity equals the product of the frequency and the wavelength. -

Chapter 24: Waves, Sound, and Light
681-S1-MSS05 8/13/04 4:59 PM Page 692 Waves, Sound, and Light Ups and Downs sections This wind surfer is riding high for now, but 1 Waves that will change soon. The energy carried by 2 Sound Waves ocean waves makes this a thrilling ride, but Lab Sound Waves in Matter other waves carry energy, too. Sound waves 3 Light and light waves carry energy that enable you Lab Bending Light to hear and see the world around you. Virtual Lab What are some Science Journal Write a short paragraph describing characteristics of waves? water waves you have seen. 692 Mark A. Johnson/CORBIS 681-S1-MSS05 8/13/04 4:59 PM Page 693 Start-Up Activities Waves Make the following Foldable to compare and con- trast the characteristics of Wave Properties transverse and compressional waves. If you drop a pebble into a pool of water, you notice how the water rises and falls as waves STEP 1 Fold one sheet of lengthwise paper in half. spread out in all directions. How could you describe the waves? In this lab you’ll make a model of one type of wave. By describing the model, you’ll learn about some properties of all waves. STEP 2 Fold into thirds. 1. Make a model of a wave by forming a piece of thick string about 50-cm long into a series of S shapes with an up and STEP 3 Unfold and draw overlapping ovals. down pattern. Cut the top sheet along the folds. 2. Compare the wave you made with those of other students. -

Chapter 1. Lattice Vibrations in One Dimension
Chapter 1. Lattice Vibrations in One Dimension Chapter 1. Lattice Vibrations in One Dimension Desolation Row Robert Wittig Sometimes I think I'm going to end up alone in a cold apartment living on cat food from a can but I guess that's not so bad since I'm a cat after all. Going Somewhere Soon Brian Andreas 121 Chapter 1. Lattice Vibrations in One Dimension 122 Chapter 1. Lattice Vibrations in One Dimension Contents 1.1. Introduction 125 A Nuanced Model 128 Coupled Wave Equations (Advanced) 130 Model Hamiltonian 133 Born and von Kármán Boundary Conditions 134 1.2. Site-to-Site Phase Progression 135 Diagram from the Hückel Model 143 Mathematical Approach from Phased Antenna Arrays 144 The Complex Plane 145 Physical Space and k-Space 145 Choices of Signs 146 Quantum Route 147 Classical Route 148 Non-Hermitian Operators Qk and Pk 150 1.3. Turning on Quantum Mechanics 151 k-Space Representation of H 153 1.4. Dispersion Relation 155 1.5. Second Quantization 157 Harmonic Oscillator: Raising and Lowering Operators 159 1.6. Interpretation 161 1.7. The Ionic Lattice 168 Amusement 170 Displacements 171 Acoustic Branch 172 Optical Branch 173 123 Chapter 1. Lattice Vibrations in One Dimension Barge Robert Wittig I pass, like night, from land to land; I have strange powers of speech; That moment that his face I see, I know the man that must hear me: To him my tale I teach. The Ancient Mariner Samuel Coleridge 124 Chapter 1. Lattice Vibrations in One Dimension 1.1. Introduction This chapter introduces and examines fundamental aspects of the vibrations that take place in periodic (crystalline) structures. -

Week 8 Packet
At Home Learning Resources Grade 6 - Week 8 Content Time Suggestions Reading At least 30 minutes daily (Read books, watch books read aloud, listen to a book, (Could be about science, social complete online learning) studies, etc) Writing or Word Work or Vocabulary 20-30 minutes daily Math 45 minutes daily Science 25 minutes daily Social Studies 25 minutes daily Arts, Physical Education, or 30 minutes daily Social Emotional Learning These are some time recommendations for each subject. We know everyone’s schedule is different, so do what you can. These times do not need to be in a row/in order, but can be spread throughout the day. Teachers will suggest which parts of the packet need to be completed or teachers may assign alternative tasks. Grade 6 ELA Week 8 Your child can complete any of the activities in weeks 1-7. These can be found on the Lowell Public Schools website: https://www.lowell.k12.ma.us/Page/3802 This week continues a focus on informational or nonfiction reading and writing. Your child should be reading, writing, talking and writing about reading, and exploring new vocabulary each week. Reading: Students need to read each day. They can read the articles included in this packet and/or read any of the nonfiction/informational books that they have at home, or can access online at Epic Books, Tumblebooks, Raz Kids, or other online books. All resources are on the LPS website. There is something for everyone. Talking and Writing about Reading: As students are reading, they can think about their reading, then talk about their reading with a family member and/or write about their reading using the prompts/questions included. -

Analytical and Computational Modeling of Mechanical Waves in Microscale Granular Crystals: Nonlinearity and Rotational Dynamics
Analytical and Computational Modeling of Mechanical Waves in Microscale Granular Crystals: Nonlinearity and Rotational Dynamics Samuel P. Wallen A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2017 Supervisory Committee: Nicholas Boechler, Chair Bernard Deconinck, GSR Ashley Emery, Reading Committee Member I. Y. (Steve) Shen Duane Storti, Reading Committee Member Program Authorized to Offer Degree: Mechanical Engineering c Copyright 2017 Samuel P. Wallen University of Washington Abstract Analytical and Computational Modeling of Mechanical Waves in Microscale Granular Crystals: Nonlinearity and Rotational Dynamics Samuel P. Wallen Chair of the Supervisory Committee: Assistant Professor Nicholas Boechler Mechanical Engineering Granular media are one of the most common, yet least understood forms of matter on earth. The difficulties in understanding the physics of granular media stem from the fact that they are typically heterogeneous and highly disordered, and the grains interact via nonlinear contact forces. Historically, one approach to reducing these complexities and gaining new insight has been the study of granular crystals, which are ordered arrays of similarly-shaped particles (typically spheres) in Hertzian contact. Using this setting, past works explored the rich nonlinear dynamics stemming from contact forces, and proposed avenues where such granular crystals could form designer, dynamically responsive materials, which yield beneficial functionality -

Local Probing of Propagating Acoustic Waves in a Gigahertz Echo Chamber
Local probing of propagating acoustic waves in a gigahertz echo chamber Martin V. Gustafsson†, Paulo V. Santos††, Göran Johansson† and Per Delsing† †Microtechnology and Nanoscience, Chalmers University of Technology, Göteborg, Sweden ††Paul-Drude-Institut für Festkörperelektronik, Berlin, Germany In the same way that micro-mechanical resonators resemble guitar strings and drums, Surface Acoustic Waves (SAW) resemble the sound these instruments produce, but moving over a solid surface rather than through air. In contrast with oscillations in suspended resonators, such propagating mechanical waves have not before been studied near the quantum mechanical limits. Here, we demonstrate local probing of SAW with a displacement sensitivity of 30amRMS/√Hz and detection sensitivity on the single-phonon level after averaging, at a frequency of 932MHz. Our probe is a piezoelectrically coupled Single Electron Transistor, which is sufficiently fast, non- destructive and localized to let us track pulses echoing back and forth in a long acoustic cavity, self- interfering and ringing the cavity up and down. We project that strong coupling to quantum circuits will allow new experiments, and hybrids utilizing the unique features of SAW. Prospects include quantum investigations of phonon-phonon interactions, and acoustic coupling to superconducting qubits, for which we present favourable estimates. Surface acoustic waves exist on scales ranging from the microscopic to the seismic and resemble ripples on a pond, but traversing the surfaces of solids. SAW with wavelengths down to the sub-micrometer range can be efficiently generated and controlled on a piezoelectric chip, using lithographically fabricated transducers and gratings. The waves experience low losses during propagation and reflection, allowing them to be harnessed for a variety of electro-mechanical microwave applications, including acoustic delay lines, resonators and filters1,2.