DOCSLIB.ORG

Intersection of Art and Science II an Educational Exhibition at the Lawson Computer Science Building Purdue University // January 8, 2018 — December 20, 2019

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Intersection of Art and Science II an Educational Exhibition at the Lawson Computer Science Building Purdue University // January 8, 2018 — December 20, 2019 Intersection of Art and Science II An educational exhibition at the Lawson Computer Science Building Purdue University // January 8, 2018 — December 20, 2019 Manuel Baez // Sarah Berube // Robert Bosch and Sage Jenson // Jean-Marc Castera // Marc and Marion Chamberland // Laura De Decker // Bathsheba Grossman // Colin Liotta // Vincent J. Matsko // Kerry Mitchell // Janna Schimka, Rolf Schmuck, and Markus Schwehm // INTERSECTION OF ART AND SCIENCE II Exhibition January 8, 2018 through December 20, 2019 Lawson Computer Science Building 3rd Floor Exhibition Space Purdue University West Lafayette, IN USA This educational exhibition examines a wide range of expressive approaches that emerge in the intersection of art, science, and technology. It is a joint collaboration between the Department of Computer Science and the Patti and Rusty Rueff School of Visual and Performing Arts at Purdue University. The exhibition was curated by Dr. Petronio Bendito and Dr. Tim Korb. Department of Computer Science cs.purdue.edu Patti and Rusty Rueff School of Visual and Performing Arts cla.purdue.edu/academic/vpa/ad Purdue University Department of Computer Science 305 N. University Street West Lafayette, IN 47907-2107 Phone: (765) 494-6010 Fax: (765) 494-0739 Intersection of Art and Science II Exhibition January 8, 2018 through December 20, 2019 Lawson Computer Science Building 3rd Floor Exhibition Area Purdue University West Lafayette, IN USA Intersection of Art and Science Exhibition II Catalog Curated by Petronio Bendito and Tim Korb Published by the Department of Computer Sciences Purdue University, West Lafayette, Indiana 47907 USA http://www.cs.purdue.edu Printed and bound in the USA by Purdue Print and Digital Services, delivered by Xerox Cataloguing Information: Art and Science Exhibition Petronio Bendito and Tim Korb (Curators, Introduction) Artists: Manuel Baez; Sarah Berube; Robert Bosch and Sage Jenson; Jean-Marc Castera; Marc and Marion Chamberland; Laura De Decker; Bathsheba Grossman; Colin Liotta; Vincent J. Matsko; Kerry Mitchell; Janna Schimka, Rolf Schmuck, and Markus Schwehm. ISBN 978-0-692-11256-4 Exhibition, Art, Computer Science, Math, Mathart, Technology, Science, Technology and Civilization, Aesthetic, Geometry, 21st Century, New Media, Painting, Photography, Digital Printmaking In addition to the current exhibition documented in this catalog, works currently on display in Lawson include the “Echo Spiral” (John Misler) stainless-steel sculpture in the Kurz Lobby, “A Parade of Algorithmic Mathematical Art” (Greg Frederickson) featuring geometric dissections, “The Quartet Collection” (Clifford Peterson) of original art that has been altered and multiplied using digital tools, and “Experience Color” (Petronio Bendito) that uses computational processes to explore digital color aesthetic. Creative Processses Involving Science, Computing and Aesthetics Petronio Bendito and Tim Korb We are pleased to showcase a new set of artworks in role that computational processes play in contemporary this 2nd edition of the Intersection of Art and Science color design methods, while “Dancing birds for Reza” Exhibition! This international invitational exhibition (Jean-Marc Castera) shows that random numbers can features fifteen artists and art collaborators that apply produce surprisingly stable results. scientific processes to the creation of visual expressions. It is the latest in a series of exhibitions that examine Students studying computer graphics use 3D printing the melding of art and science in the creation of visual to help visualize complex computer models and expressions, a goal stretching back to 2005 during the mathematical shapes—“Double Schwarz D” (Bathsheba planning of the Lawson Computer Science Building. It Grossman) and “Entangled Snowflakes” (Sarah Berube) contributes to the creation of a teaching, learning, and are printed 3D models of a minimal surface (like a soap working environment that inspires and engages students, bubble) and an icosahedron of snowflakes (like a soccer faculty, and visitors. By fostering computational visual ball), respectively. Translating continuous equations literacy, it is our hope that the works in the exhibit will into discrete steps is central to much of numerical promote collaborations and interdisciplinary thinking and computing—“Exploding Outwards” (Colin Liotta) shows educate our students to engage with the increasingly that the discrete nature of a physical model with repeating growing role that computational and visual processes play pieces can lead to a continuous view. in the creation of real and virtual experiences. Quantum computing involves collaboration among Participating artist Jean-Marc Castera points out that a computer scientists, physicists, and engineers in the practice based on art and science eliminates a feeling development of arguably the next frontier in computing— of ”any discontinuity between a left and right part of [his] “Interference Pattern of Quantum Random Walk” (Laura brain.” Several of the works in this exhibition have a De Decker) illustrates one of the complex and non- direct connection to computer science education, and intuitive concepts in the quantum universe. Modeling even art history. For example, in beginning computer life itself is another leap in computing—“Turing-McCabe science classes, students learn about the importance Pattern” (Janna Schimka, Rolf Schmuck, and Markus of binary concepts—“Kandinsky in Binary” (Marc and Schwehm) explores real-time use of these patterns to Marion Chamberland) and “Sierpinski” (Vincent J. understand movement, music, and visuals. Matsko) illustrate binary numbers and binary trees, respectively. Visually, they show the possibilities in Some real-world objects with complex shapes and combining geometric shapes and color to suggest rhythm, physical properties are extraordinarily difficult to model organization, and, in the case of Sierpinski, texture. A with computer algorithms—the wooden shapes in “The common solution to the knight’s tour chess problem is Light Keeper” (Manuel Baez) illustrate this challenge to often used to illustrate recursive programming, a tricky computer model makers. subject with which beginning students often struggle— “The Knight Tours the Castle” (Robert Bosch and Sage As showcased in this exhibit, math and computing Jenson) is an elegant depiction of one solution to this processes are powerful creative tools. We hope this puzzle. It exemplifies the role that constraints play in exhibition contributes to building a great understanding building a cohesive visual expression. More advanced of how art and science are not mutually exclusive. computer science students learn about fractals and the The works exhibited characterize new possibilities of properties of random numbers—“Newton in Wackyland” human experiences and expressions—from purely (Kerry Mitchell) is an innovative, artistic application of aesthetic enjoyment to the development of deep and Newton’s methods to fractals. It also shows the increasing sophisticated concepts. 3 The Light Keeper (2014-2016) emergence topology by Manuel Báez complexity bio-design Snap to grid version 25” x 25” self-organization morphology Originally Ceremonial Space, 21 foot diameter Birch Plywood, Wiremesh, Stainless Steel Fittings My work as an architect and artist draws inspiration ends overlap, a central pivoting joint allows the ends to rotate, from the forms, structures, and integrative systems deforming the frame and re-aligning the end corners. This generated by elemental processes that exist throughout allows for extension strips to be added and woven together the natural environment and how related developments through their de-formability. The circular frame, pivoting in science and mathematics can provide insights into joint, and woven extension sequences generated the overall their inner workings. Modern analytical tools and such emergent design patterns. Similarly, the interactions between related theories as Complexity and Emergence are the round wires of the mesh and the hinging origami folds revealing a richly diverse morphological realm with are the source of the membrane’s emergent de-formability. implications towards architecture, engineering, design, Thus, dynamic circularity is inherently embodied throughout art, and other disciplines. This deeper understanding the design reflecting its form generating capabilities through a of complex phenomena reveals how these fertile material and dynamic configuration. processes inherently engage elemental relationships that dynamically evolve into rhythmically-entrained patterns within highly integrative systems. The analysis of this generative potential and its interrelated cellular units and Manuel Báez // Carleton University, Azrieli School of self-organizing patterns can yield more comprehensive Architecture and Urbanism, Canada. Báez has been at understanding of emergent complex morphology. Carleton University since 2001. Previously, he taught at The Cooper Union for the Advancement of Science and The Light Keeper is made from two basic materials: 1/8” Art in New York City and Rhode Island School of Design thick birch plywood, cut along the grain into 5’ long and in Providence, RI. The eminent scholar Martin Kemp has 4” wide malleable strips and woven wiremesh fabric. The featured Báez’s research in Structural Intuitions: Seeing de-formability of the plywood strips is explored through Shapes in Art and Science, 2016. Recently, Báez won the the inherent morphological shapes that can be
Load more

Recommended publications
  • THIAGO JOSÉ CÓSER Possibilidades Da Produção Artística Via
    THIAGO JOSÉ CÓSER Possibilidades da produção artística via prototipagem rápida: processos CAD/CAM na elaboração e confecção de obras de arte e o vislumbre de um percurso poético individualizado neste ensaio. Dissertação apresentada ao Instituto de Artes da Universidade Estadual de Campinas, para a obtenção do título de mestre em Artes. Área de concentração: Artes Visuais Orientador: Prof. Dr. Marco Antonio Alves do Valle Campinas 2010 3 FICHA CATALOGRÁFICA ELABORADA PELA BIBLIOTECA DO INSTITUTO DE ARTES DA UNICAMP Cóser, Thiago José. C89p Possibilidades da produção artística via Prototipagem Rápida: Processos CAD/CAM na elaboração e confecção de obras de arte e o vislumbre de um percurso poético individualizado neste ensaio. : Thiago José Cóser. – Campinas, SP: [s.n.], 2010. Orientador: Prof. Dr. Marco Antonio Alves do Valle. Dissertação(mestrado) - Universidade Estadual de Campinas, Instituto de Artes. 1. Prototipagem rápida. 2. Arte. 3. Sistema CAD/CAM. 4. Modelagem 3D. 5. escultura. I. Valle, Marco Antonio Alves do. II. Universidade Estadual de Campinas. Instituto de Artes. III. Título. (em/ia) Título em inglês: “Possibilities of Art via Rapid Prototyping: using CAD / CAM systems to create art works and a glimpse of a poetic route individualized essay.” Palavras-chave em inglês (Keywords): Rapid prototyping ; Art ; CAD/CAM systems. ; 3D modelling ; Sculpture. Titulação: Mestre em Artes. Banca examinadora: Prof. Dr. Marco Antonio Alves do Valle. Profª. Drª. Sylvia Helena Furegatti. Prof. Dr. Francisco Borges Filho. Prof. Dr. Carlos Roberto Fernandes. (suplente) Prof. Dr. José Mario De Martino. (suplente) Data da Defesa: 26-02-2010 Programa de Pós-Graduação: Artes. 4 5 Agradecimentos Ao meu orientador, profº Dr.
    [Show full text]
  • Momath's Intersection of Math And
    Bridges 2020 Conference Proceedings Composite: MoMath’s Intersection of Math and Art Cindy Lawrence1 and Tim Nissen2 1Cindy Lawrence, National Museum of Mathematics, NYC; [email protected] 2Tim Nissen, National Museum of Mathematics, NYC; [email protected] Abstract That there are meaningful connections between art and mathematics is intuitively clear to mathematicians and mathematically-inspired visual artists, but the connection is often less clear to others, especially to those whose negative associations with mathematics during school-age years trigger emotions counter to feelings inspired by beautiful artworks. At the National Museum of Mathematics, the Composite gallery has been a laboratory of temporary art exhibitions. The introduction of tactile interactivity as a bridge between art and geometric forms in Solid Math, and the presentation of origami art through its often-overlooked mathematical makeup in Math Unfolded, highlighted these interconnections for visitors of all ages. New in Composite Since 2014, Composite, the gallery at the National Museum of Mathematics (MoMath) [2], has housed a series of temporary exhibitions of the work of mathematically-inclined artists including Antal Kelle ArtFormer, Miguel Berrocal, Matthew Brand, and Trevor and Ryan Oakes. In 2019, two exhibitions explored the connections between mathematics and art through multi-artist curated shows and physical interactives. Characteristic of the Museum proper, the collection of works and interactives encourages visitors to engage deeply with the content, integrating an array of models and artworks.. Solid Math, which ran from April through July of 2019, explored the geometry of regular polyhedra and showcased art based on these forms. Platonic, Archimedean, and Catalan polyhedra provided the formal constraints as well as the rhythmic underpinnings for the artists’ pieces presented in the show.
    [Show full text]
  • Bathsheba Grossman
    gallery: bathsheba grossman “The universe is orderly and friendly and beautiful. Structure is this lovely, versatile thing.” “It’s either right or it’s wrong. It’s either elegant or not elegant. In math, those are actual properties. Everyone agrees.” 24 Based on mathematical structures, Bathsheba Grossman’s metal artworks are an example of digital sculpture given form. by Raven Hanna Bathsheba Grossman carries around her art wher- grasp. As you attempt to trace the labyrinthine for- ever she goes. She shows strangers her two- mations, you are drawn in, mesmerized. inch metal sculptures, the babies of her collection. Although her sculptures look mathematical, the People hold them, stare at them, love them, and quantitatively-challenged are not put off. “A lot buy them. In this way, she has sold on the spot to of people who don’t know anything about math or barmaids, secretaries, bus drivers, and mail deliverers. science buy these things,” she says. “There’s a The sculptures themselves are their own best lot of raw appeal. People approach them in different marketing. After selling a sculpture to Microsoft’s ways, but almost everybody sees that they are Mark Zbikowski, famous to computer geeks and of interest.” business buffs for developing MS-DOS software, Grossman grew up in a middle-class neighbor- she watched requests from other Microsoft employ- hood in Massachusetts with English professor ees roll in. Grossman makes art people want. parents. At Yale University, she shirked the family “I think they say something important about the tradition by pursuing a degree in mathematics.
    [Show full text]
  • Galerije Antuna Augustin^I]A Original U Skulpturi
    28–29 ANALI ANALI GALERIJE ANTUNA AUGUSTIN^I]A GOD. XXVIII–XXIX (2008.–2009.) • BR. 28–29 • STR. 1–472 • KLANJEC 2010. Simpozij ORIGINAL U SKULPTURI Klanjec, 4. – 6. lipnja 2008. ZBORNIK RADOVA 28 29 ISSN-0352-1826 UDK 71/77(058) ANALI GALERIJE ANTUNA AUGUSTIN^I]A GOD. XXVIII–XXIX (2008.–2009.) • BR. 28–29 • STR. 1–472 • Klanjec 2010. ISSN-0352-1826 UDK 71/77(058) CONTENTS SADR@AJ Editor’s Word Riječ urednika 5 5 LAVINIA BELUŠIĆ LAVINIA BELUŠIĆ The Concept of Originality in Pojam izvornosti u traktatima Rennaisance Italy Treatises (1435–1568) renesansne Italije (1435.–1568.) 35 9 IGOR FISKOVIĆ IGOR FISKOVIĆ The Case of the Renaissance Sculpture Slučaj renesansnog kipa Sv. Petra u of St. Peter in Vrboska Vrboskoj 51 37 VEDRANA GJUKIĆ-BENDER VEDRANA GJUKIĆ-BENDER Sculptor Innocenzo Spinazzi, Creator Innocenzo Spinazzi – kipar stvaratelj and Copyist i kopist 64 53 VESNA LOVRIĆ PLANTIĆ VESNA LOVRIĆ PLANTIĆ »The Montgolfier Brothers’ Balloon« »Balon braće Montgolfier« Luxurious Clock-Sculpture: Problems of Raskošan sat-skulptura: problemi Attribution and Dating atribucije i datacije 84 67 DR. JOSIP KOROŠEC JOSIP KOROŠEC The Role of Sculpture and the Uloga skulpture i značaj njezine Importance of Its Originality izvornosti 96 85 CONTENTS SADR@AJ MARTINA OŽANIĆ MARTINA OŽANIĆ Sculptural Group of The Holy Family – Skulpturalna grupa Svete Obitelji – Sharing Ideas and Authorship in pitanje udjela autorske invencije u Studies and Prints odnosu na grafički predložak 113 97 ANICA RIBIČIĆ-ŽUPANIĆ ANICA RIBIČIĆ-ŽUPANIĆ Francisco Pallas y Puig Francisco
    [Show full text]
  • Bruce Beasley Oakland, California, USA
    Brown Symposium XXXVII at Southwestern University What Things May Come: The Third International 3D Print Sculpture exhibition Artists’ Biographies and Statements Bruce Beasley Oakland, California, USA Biography: Bruce Beasley is one of the United States most prominent sculptors. In 1962 The Museum of Modern Art in New York acquired one of Beasley’s sculptures making him the youngest artist ever to be included in their permanent collection. In 1963, he won the purchase prize in the Paris Biennale, the world’s most prestigious international exhibition. Since that time Beasley has had his sculptures included in the permanent collection of 33 art museums around the world. He has had over 55 solo exhibitions in the US and abroad and has been included in hundreds of important group exhibitions. He has represented the United States in numerous international Biennale exhibitions and world fairs. Beasley has done 35 monumental sculpture commissions in the United States and abroad. Including sculptures for the Beijing Olympic Games and the Shanghai world expo. He has just completed a large granite sculpture for the city of Palo Alto, and he currently has a solo exhibition of 5 large sculptures on the campus of the University of California at Berkeley. www.BruceBeasley.com Artist Statement: I began working with 3D computer modeling in 1987. The issue that drew me to computer modeling was the desire to be able to manipulate and intersect shapes easily and spontaneously, free of the constraints of real material. My background is the direct metal working tradition of sculpture, where the esthetic composition and physical making of the sculpture are one and the same.
    [Show full text]
  • Tesis Margarita Rodríguez Ibáñez
    UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS DE LA INFORMACIÓN Departamento de Comunicación Audiovisual y Publicidad II TESIS DOCTORAL Cambios producidos en al arte por su inclusión en el sistema-red MEMORIA PARA OPTAR AL GRADO DE DOCTOR PRESENTADA POR Margarita Rodríguez Ibáñez Directora Pilar Aumente Rivas Madrid, 2017 © Margarita Rodríguez Ibáñez, 2010 CAMBIOS PRODUCIDOS EN EL ARTE POR SU INCLUSIÓN EN EL SISTEMA-RED TESIS DOCTORAL Margarita Rodríguez Ibáñez Dirigida por Dª. Pilar Aumente Rivas Departamento CAVP II Facultad de Ciencias de la Información UNIVERSIDAD COMPLUTENSE DE MADRID Hechos futuros son todos aquellos que habrán de tener lugar y, por consiguiente, habrán de ser enteramente determinados y sus representaciones o, lo que es lo mismo, sus adivinaciones, singulares y, por tanto, altamente poéticas. Alex Gottilieb Baumgarten Reflexiones filosóficas en torno al poema , 1735, § LXI 2 ÍNDICE ASPECTOS METODOLÓGICOS I. INTRODUCCIÓN Pág. 9 II. OBJETO DE LA INVESTIGACIÓN Pág. 10 III. OBJETIVOS DE LA INVESTIGACIÓN Pág. 11 IV. PREGUNTAS Pág. 11 V. ESTADO DE LA CUESTIÓN Pág. 12 VI. METODOLOGÍA Pág. 21 VII. VALIDEZ Pág. 23 VIII. RESUMEN Pág. 26 INTRODUCCIÓN 1. INTRODUCCIÓN: Pág. 28 PARADIGMA SISTEMA RED 2. CANAL INTERNET: Pág. 41 2.1. Internet y la Web. Pág. 41 2.2. Alcance y progresión. Pág. 42 2.3. Cambios paradigmáticos comunicacionales Pág. 44 2.4. La sociedad informacional Pág. 50 3. EL CIBERESPACIO. Pág. 54 3.1. Las interfaces y programas Pág. 64 3.2. El hipertexto Pág. 65 3.3. Multimedia e Hipermedia Pág. 68 3.4. La interactividad Pág. 70 3.5. Lo virtual Pág. 74 3 3.6.
    [Show full text]
  • Estimular El Crecimiento De Bacterias Para Mejorar Los
    BIOLOGÍA Los investigadores vieron el cambio de contar con los dedos Los hallazgos permiten un soporte empírico más fuerte para la en el momento de empezar a basarse en la memoria cuando existencia de teorías sobre el desarrollo de las matemáticas, en repitieron el experimento un año después con los niños. En palabras de Jessica Cantlon, neurocientífica cognitiva en la esta segunda vez, los niños contaban menos con los dedos y Universidad de Rochester, en Nueva York. Pero añade que: “no APRENDIENDO A SUMAR hacían menos movimientos labiales (como contando en voz sabemos qué información es la que pasa entre el hipocampo alta) que la primera vez. Para poder saber qué pasa realmen- y el neocórtex”. Una manera de demostrar esta cuestión sería DE CABEZA: ¿QUÉ OCURRE te en el cerebro mientras se efectúa una tarea así, se recurrió extender el estudio a niños con el hipocampo dañado o con a la imagen por resonancia magnética funcional (FMRI, por alguna discapacidad en el aprendizaje de las matemáticas. EN EL CEREBRO? sus siglas en inglés). Básicamente, con esta técnica se puede Por Cristóbal Rodero ver qué zonas del cerebro se utilizan más en un determinado Menon sugiere que la maduración del hipocampo y sus conexio- momento en función de la cantidad de sangre que llegue, y nes esconden probablemente no solo el desarrollo de habilida- Recuerdo que en el colegio, para sumar primero me enseñaron en el caso del experimento que estamos comentando, el ele- des matemáticas basadas en la memoria, sino también algún otro con objetos físicos, de ahí a escribir palitos en el papel, lue- gido fue el hipocampo.
    [Show full text]
  • Mathematics and Arts
    Mathematics and arts a classification of mathematical sculpture Ricardo Zalaya, Javier Barrallo Polytechnic University of Valencia, University of the Basque Country [email protected],[email protected] Abstract: In this paper, we define the term Mathematical Sculpture, a task somehow complex. Also, we present a classification of mathematical sculptures as exhaustive and complete as possible. Our idea consists in establishing general groups for different branches of Mathematics, subdividing these groups according to the main mathematical concepts used in the sculpture design. Keywords: Mathematical sculpture Introduction There are several studies on the so-called Mathematical Sculpture, a concept that we will try to define in the next section. These studies deal with specific aspects, such as the mathematical study of the works of a particular sculptor or the analysis of specific types of mathematical sculptures. Also, there are general studies. However, as far as we know, there is no work in the scientific literature providing a systematic analysis of the connections between mathematics and sculpture. Neither is there any study that offers a complete and exhaustive classification of mathematical sculpture. The scarcity and lack of research on this artistic topic led us to choose it as the main topic of the doctoral thesis developed by Ricardo Zalaya, assistant lecturer at the Polytechnic University of Valencia, tutored by Javier Barrallo, professor at the University of the Basque Country, Spain. In this paper we propose a classification for mathematical sculpture, based on the results of our research in the last years, and on the comments and observations provided by other experts on the topic.
    [Show full text]
  • Front Cover 3/16/07 8:54 PM Page 1 Cover 2 3/18/07 8:15 PM Page 2
    Front Cover 3/16/07 8:54 PM Page 1 Cover 2 3/18/07 8:15 PM Page 2 Team Minnesota Sculpts Winning Mathematical Art Stan Wagon Macalester College Stan Wagon Rhapsody in White, Second Place, 2000 Artists’ Choice, People’s Choice Robert Longhurst, designer Stan Wagon A Twist in Time Honorable Mention, 2002 Bathsheba Grossman, designer Stan Wagon Whirled White Web, Second Place, 2003 US Snow Sculpture of the Year Brent Collins and Carlo Séquin, designers Rich Seeley At the 2007 Breckenridge International Snow Sculpture Competition, the Minnesota team of David Chamberlain, Stan Wagon, Dan Schwalbe, Rich Seeley, and Beth Seeley won second place. A spokesperson for the team explained, “the most difficult artistic decision was whether to carve a rectangular box or a perfect cube with a base.” Team Minnesota has a long and successful history of carving beautiful surfaces (see images to the right). Carl Scofield stanwagon.com Stan Wagon teaches mathematics at Macalester College and his web page Cool Jazz, Second Place, 2007 has complete records of the team’s snow sculpting work. David Chamberlain, designer pp.03-04 3/25/07 10:35 PM Page 3 In this Issue Team Minnesota Sculpts Winning Mathematical Art 2 Stan Wagon Math Horizons is for undergraduates and How to sculpt the perfect ice cube. others who are interested in mathematics. Its purpose is to expand both the career and Pythagoras’s Darkest Hour 5 intellectual horizons of students. Colin Adams Truth, betrayal, and hemlock! ARTHUR T. BENJAMIN Harvey Mudd College Hide and Seek 7 JENNIFER J. QUINN Andy Martin Association for Women in Mathematics Drawing a circle around every rational number covers every irrational number, right? Editors When Lions Battle 8 CAROL BAXTER Nicholas Tasaday Managing Editor & Art Director New documents suggest a Newton-Leibniz collaboration.
    [Show full text]
  • O O O N III: 1&1 II :Ii .1&1 U 1&1 A
    at THE NEWSLETTER OF THE MATHEMATICAL ASSOCIATION OF AMERICA .: 1&1 II :I ::::» z o N 1&1 :I .::::»... o > o o o N III: 1&1 II :Ii .1&1 U 1&1 a INSIDE: Art Inspired hy Mathcmatics in New York ................................................................................ .4 (;conlctry for a New (:entury ..................................................................................................... 1) Ah'lI1doning De.ld Ends: Emhmdng Lively Beginnings .......................................................... J() The Brain in the Box ................................................................................................................. 1J FOCUS DECEMBER 2000 FOCUS IS published by the Mathematical Association of America in January, February, March, April, Mayl)une, August/September, October, November. and a FOCUS December. Editor: Fernando Gouvea. Colby College; [email protected] December 2000 Managing Editor: Carol Baxter. MAA Volume 20, Number 9 [email protected] Senior Writer: Harry Waldman. MAA [email protected] Inside Please address advertising inquiries to: Kate 4 Art Inspired by Mathematics in New York Debelack. MAA; [email protected] By Ivars Peterson President: Thomas F. Banchoff. Brown University 6 Science and Technology Policy Site Now Part of MAA Online First Vice-President: Barbara L. Osofsky. By Al Buccino Second Vice-President: Frank Morgan. Secretary: Martha J. Siegel. Associate Secretary: James J. Tattersall. Treasurer: 8 MAA Issues Revised Guidelines for Undergraduate Gerald J. Porter Programs and Departments Executive Director: Tina H. Straley By John Fulton Associate Executive Director and Director of Publications and Electronic Services: 9 Geometry for a New Century Donald J. Albers By Joseph Malkevitch FOCUS Editorial Board: Gerald Alexanderson; Donna Beers; J. Kevin 10 Abandoning Dead Ends: Embracing Lively Beginnings Colligan; Ed Dubinsky; Bill Hawkins; Dan By Edward B. Burger and Michael Starbird Kalman; Maeve McCarthy; Peter Renz; Annie Selden; Jon Scott; Ravi Vakil.
    [Show full text]
  • Mathematical Sculpture Classification
    ISAMA BRIDGES The International Society of the Mathematical Connections Arts, Mathematics, and Architecture in Art, Music, and Science Mathematical Sculpture Classification Ricardo Zalaya * & Javier Barrallo ** * Universidad Politecnica de Valencia ** Universidad del Pais Vasco SPAIN E-mail: [email protected] Abstract The introduction of mathematical sculpture in advanced education needs a taxonomy to classify all the different types of sculpture. From our point of view, this classification has never been arranged deeply. This paper is a first attempt to that classification. We expect to receive suggestions from the Art and Mathematics community in order to start a work that we will take away during the next two years.and whose first step is given with this paper. As a preliminary starting point we have suggested the following nine categories for mathematical .sculpture: I. Polyhedral and classic geometry, II. Non-oriented surfaces, lli. Topological knots, IV. Quadrics and ruled surfaces, V. Symmetric and modular structures, VI. Boolean operations, VII. Minimal surfaces, Vlli. Transformations IX. Others. 1. What is mathematical sculpture? It is surprising that after so many Art & Math, ISAMA and Bridges Conferences, only a reduced number of participants has previously discussed a classification for mathematical sculpture and, as far as we know, never this task has been made with enough accuracy so as be taken as a guide for educators or people deeply interested on the topic. From our point of view, the introduction of mathematical sculpture in schools or universities requires a classification to frame the sculptures in different categories according to the mathematical concepts that they represent. Without that classification, mathematical sculpture can only be introduced in the classroom as a mere slideshow session that, although can be interesting, is not appropriate to teach this topic into high-level courses.
    [Show full text]
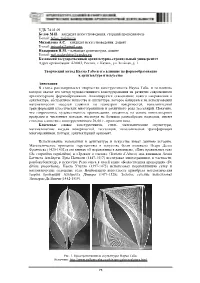
  • УДК 74.01.09 Белов М.И. – Кандидат Искусствоведения, Старший Преподаватель E-Mail: Belov [email protected] Михайлова А.С
    УДК 74.01.09 Белов М.И. – кандидат искусствоведения, старший преподаватель E-mail: [email protected] Михайлова А.С. – кандидат искусствоведения, доцент E-mail: [email protected] Надыршин Н.М. – кандидат архитектуры, доцент E-mail: [email protected] Казанский государственный архитектурно-строительный университет Адрес организации: 420043, Россия, г. Казань, ул. Зелёная, д. 1 Творческий метод Наума Габо и его влияние на формообразование в архитектуре и искусстве Аннотация В статье рассматривается творчество конструктивиста Наума Габо, и то влияние которое оказал его метод художественного конструирования на развитие современного архитектурного формообразования. Анализируется становление нового направления в архитектуре, абстрактном искусстве и скульптуре, которое базируется на использовании математических моделей сложных по геометрии поверхностей, топологической трансформации классических многогранников и различного рода тесселяций. Показано, что современные художественные произведения, созданные на основе компьютерных программ и численных методов, несмотря на большое разнообразие подходов, имеют стилевое единство с конструктивизмом 20-60 г., прошлого века. Ключевые слова: конструктивизм, стиль, математические скульптуры, математические модели поверхностей, тесселяция, топологическая трансформация многогранников, паттерн, архитектурный орнамент. Использование математики в архитектуре и искусстве имеет давнюю историю. Математические принципы перспективы в искусстве были изложены Пьеро Делла Франческа (1420-1492) в его книгах «О перспективе
    [Show full text]