The Olympic 500M Speed Skating
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
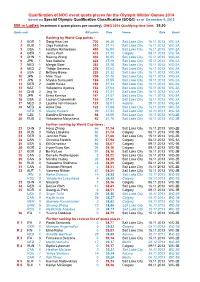
Qualification of NOC Event Quota Places for the Olympic Winter Games 2014 Based on Special Olympic Qualification Classification (SOQC) As of December 9, 2013
Qualification of NOC event quota places for the Olympic Winter Games 2014 based on Special Olympic Qualification Classification (SOQC) as of December 9, 2013 500 m Ladies (maximum 4 quota places per country) OWG 2014 Qualifying time limit: 39,50 Quota rank WC points Time Venue Date Event Ranking by World Cup points : 1 KOR 1 Sang-Hwa Lee 700 36,36 Salt Lake City 16.11.2013 WC-2A 2 RUS 1 Olga Fatkulina 510 37,13 Salt Lake City 16.11.2013 WC-2A 3 USA 1 Heather Richardson 490 36,90 Salt Lake City 16.11.2013 WC-2A 4 GER 1 Jenny Wolf 473 37,14 Calgary 08.11.2013 WC-1A 5 CHN 1 Beixing Wang 430 36,85 Salt Lake City 15.11.2013 WC-2A 6 JPN 1 Nao Kodaira 322 37,29 Salt Lake City 15.11.2013 WC-2A 7 NED 1 Margot Boer 262 37,28 Salt Lake City 15.11.2013 WC-2A 8 NED 2 Thijsje Oenema 258 37,62 Salt Lake City 16.11.2013 WC-2A 9 USA 2 Brittany Bowe 220 37,32 Salt Lake City 15.11.2013 WC-2A 10 JPN 2 Maki Tsuji 209 37,70 Salt Lake City 15.11.2013 WC-2A 11 JPN 3 Miyako Sumiyoshi 186 37,55 Salt Lake City 15.11.2013 WC-2A 12 GER 2 Judith Hesse 180 37,34 Salt Lake City 16.11.2013 WC-2A 13 KAZ 1 Yekaterina Aydova 162 37,64 Salt Lake City 15.11.2013 WC-2A 14 CHN 2 Jing Yu 142 37,31 Salt Lake City 16.11.2013 WC-2A 15 JPN 4 Erina Kamiya 141 37,57 Salt Lake City 16.11.2013 WC-2A 16 USA 3 Lauren Cholewinski 135 37,60 Salt Lake City 15.11.2013 WC-2A 17 NED 3 Laurine van Riessen 122 38,01 Astana 29.11.2013 WC-3A 18 NED 4 Anice Das 122 37,84 Salt Lake City 15.11.2013 WC-2A NED 5 Mayon Kuipers 99 37,92 Salt Lake City 16.11.2013 WC-2A 19 CZE 1 Karolina Erbanová 94 38,09 -

Olympische Kwalificatiewedstijden
ISU WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2019 FEBRUARY, 23 and 24, 2019; ICESTADIUM THIALF - HEERENVEEN Table of contents page 1. World records, World records Jun. ,Track records and Championship records 2, 3 2. Country records 4 3. List of the World Champions Sprint and the numbers 2 and 3 5 – 8 4. Medals Classification World Sprint Championships Ladies and Men 9 - 11 5. Personal Best Ladies and Men 12 - 15 6. Results in previous World Championships Sprint 16, 17 7. Intermediate times and Lap times WR, TR and CR 18 8. Top 10 Ladies and Men in Thialf-Heerenveen 19, 20 February,20; 2019 Statistical Speed Skating Documentation compiled by Ronald Kruit and Alex Dumas ISU WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2019 FEBRUARY, 23 and 24, 2019; ICESTADIUM THIALF - HEERENVEEN Records Ladies 500 meter World record 36,36 Sang-Hwa (KOR) Salt Lake City 16-11-2013 World record Jun. 37,78 Min Seon Kim (KOR) Salt Lake City 08-12-2017 Dutch record 37,06 Thijsje Oenema (NED) Salt Lake City 27-01-2013 Track record 37,17 Nao Kodaira (JPN) Heerenveen 15-12-2018 Championship record 36,75 Nao Kodaira (JPN) Calgary 25-02-2017 1000 meter World record 1.12,09 Nao Kodaira (JPN) Salt Lake City 10-12-2017 World record Jun. 1.14,21 Joy Beune (NED) Salt Lake City 10-03-2018 Dutch record 1.12,53 Jorien ter Mors (NED) Calgary 25-02-2017 Track record 1.13,24 Brittany Bowe (USA) Heerenveen 16-12-2018 Championship record 1.12,28 Heather Bergsma (USA) Calgary 26-02-2017 Points Sprint Combination World record 146.390 Nao Kodaira (JPN) Calgary 25/26-2-2017 (36,75 – 1.12,51 – 36,80 – 1.13,17) World record Jun. -

8.5X11 Event Poster V9
SALT LAKE CITY, UTAH - JANUARY 26 & 27, 2013 WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2013 Essent ISU World Sprint Championships Kearns, Utah Saturday, January 26 & Sunday, January 27, 2013 Ladies and Mens Sprint - Competition start 1:00 p.m. ADULT GENERAL ADMISSION - $5.00 SENIOR/CHILD GENERAL ADMISSION - $2.50 VIP HOSPITALITY PACKAGE AVAILABLE online, www.UtahOlympicLegacy.com Utah Olympic Oval 5662 South Cougar Lane, Kearns, Utah www.UtahOlympicLegacy.com - 801-968-6825 LOCAL SPONSORS JournalsTHE VALLEY ISU Representatives: ISU Council Member Roland Maillard, Switzerland ISU Medical Advisor Dr. Joel Shoebe, USA ISU TC Representative Jildou Gemser, Netherlands Referee Men Erik Osmundset, Norway Assistant Referee Men Paul Stangl, USA Referee Ladies Helmut Ripper, Germany Assistant Referee Richard Hunt, Canada Starter Men Jan Zwier, Netherlands Assistant Starter Men Bruce Lance, USA Starter Ladies Ake Falk, Sweden Assistant Starter Ladies Takeshi Ushida, Japan Utah Olympic Oval Organizing Committee Chair of the Organizing Committee Kari Holt Larson VP Sport & Venue, Marc Norman Sport Services Manager Ann Pearson Competition Services Manager Todd Porter Marketing Manager Tina Esparza Operations Manager Kurt Warren Spectator Services Manager Bob Garcia Staff/Vol Services Manager Amber Clark Technical Volunteer Manager KD Todd Broadcast/Sport Production Manager Derek Parra Accreditation Manager Arlo Anderson Venue Press Chief Lisa Valent Chief Medical Officers Joel Shobe Doping Control Officer Gary Robbins Technical Volunteers: Finish Lynx -

Finishlynx Sports Timing Systems
FinishLynx Timing & Results Systems Lynx System Developers Lynx System FinishLynx Sports Timing & Event Management Solutions July 2017 INTERNATIONAL SPORTS TIMING PACKAGES CONTENTS Description Page Regulatory Acceptance and Reference Letters 4 Athletics – Photo-Finish and Timing for Track Events 6 Athletics - False Start Detection 8 Athletics - Field Events 9 Canoe - Kayak - Rowing – Photo-Finish and Timing 10 Cycling – Photo-Finish and Timing 12 Speed Skating – Photo-Finish and Timing 14 High Velocity Sports – Photo-Finish and Timing 16 Pari-Mutuel Sports – Photo-Finish and Timing 16 Reference Venues & Events 20 www.finishlynx.com PAGE 2 INTERNATIONAL SPORTS TIMING PACKAGES 3 KEY REASONS TO CHOOSE LYNX SIMPLE AND POWERFUL FinishLynx technology incorporates two decades of industry and customer feedback, 1 which yields products that are powerful, customizable, and easy to use. Underlying all Lynx products is a philosophy that all our products should link together seamlessly. This idea of links between products is the motivation for the company name: Lynx. This seamless product integration ensures that producing accurate results is easy. From start lists, to results capture, to information display―data flows instantly and automatically with FinishLynx. MODULAR AND EXPANDABLE The entire Lynx product line is designed so the customer can easily expand in two ways: by 2 adding new products or by upgrading existing ones. Customers can feel confident knowing that if they choose an entry-level system, they can always upgrade to a higher level at a later date. Our commitment to ongoing development means that enhancements are constantly added to our hardware, software, and third-party integration. And thanks to our commitment to free software updates, you can always download the latest software releases right from our website. -

MISTRZOSTWA ŚWIATA NA DYSTANSACH (Mężczyźni - Kobiety)
MISTRZOSTWA ŚWIATA NA DYSTANSACH (Mężczyźni - Kobiety) Pierwsze Mistrzostwa Świata na Dystansach rozegrane zostały w Hamar w Norwegii w roku 1996. W latach Igrzysk Olimpijskich poza rokiem 1998 - I.OL. w Nagano Mistrzostw nie organizowano. Polacy - mężczyźni startowali we wszystkich rozgrywanych Mistrzostwach, kobiety natomiast w latach 1996 - 1999 i 2003 roku w Mistrzostwach Świata ma Dystansach nie występowały. * Mistrzowie - Mistrzynie Świata. 1996 HAMAR 500 m. Hiroyasu SHIMIZU JPN 35,91 / 36,15 72,060 * Tomasz ŚWIST 37,41 / 37,60 75,010 17 miejsce 1000 m. Sergiej KLEWCZENIA RUS 1:13,30 Paweł ZYGMUNT 1;16,24 22 miejsce Tomasz ŚWIST upadek 1500 m. Jeroen STRAATHOF NED 1:53,94 Paweł ZYGMUNT 1:56,63 13 miejsce 5000 m. Ids POSTMA NED 6:47,09 Jaromir RADKE 6:57,29 11 miejsce 10000 m. Gianni ROMME NED 14:05,46 Jaromir RADKE 14:37,38 12 miejsce 1997 WARSZAWA 500 . Manabu HORII JPN 37,08 / 36,47 73,550 Tomasz ŚWIST 38,21 / 38,11 76,320 20 miejsce 1500 m. Jeroen STRAATHOF NED 1:56,57 Artur SZAFRAŃSKI 2:00,63 18 miejsce 1998 CALGARY 500 m. Hiroyasu SCHIMIZU JPN 35,36 / 34,82 70,180 Paweł ABRATKIEWICZ 35,89 / 35,89 71,780 9 miejsce Tomasz ŚWIST 36,06 / dysk. 1000 m. Sylwain BOUCHARD CAN 1:09,60 Paweł ABRATKIEWICZ 1:11,38 15 miejsce 1999 HEERENVEEN 500 m. Hiroyasu SHIMIZU JPN 35,43 / 35,26 70,690 Paweł ABRATKIEWICZ 36,17 / 35,99 72,160 6 miejsce Tomasz ŚWIST 35,84 / 36,34 72,180 7 miejsce 1000 m. -

Herziene Druk, © Margriet De Schutter Eindredacteur
Herziene druk, !"#$ © !"#$ Margriet de Schutter Eindredacteur: Anne Marie Westra-Nijhuis Portretfoto voorkant: Monique Zomer - Goodlookz Fotogra%e Actiefoto voorkant: Soenar Chamid Actiefoto Dennis van der Geest, Bram Ronnes, Rintje Ritsma, Stefan Groothuis, Christijn Groeneveld, Regi Blinker & actie- en portretfoto Mark Huizinga, Yvonne van Gennip, Erben Wennemars, Jochem Uytdehaage: Soenar Chamid Actiefoto Frank Groenendaal: Frank van Boxtel Portretfoto’s Dennis van der Geest, Bram Ronnes, Frank Groenendaal, Regi Blinker en Rintje Ritsma zijn persoonlijk eigendom en exclusief beschikbaar gesteld voor dit boek. Actie- en portretfoto’s Pieter van den Hoogenband, Peter Blangé, Ada Kok en Verona van de Leur zijn persoonlijk eigendom en exclusief beschikbaar gesteld voor dit boek. Producent: Free Musketeers, Zoetermeer www.freemusketeers.nl ISBN: &'(-&"-(!$)$)-"-' NUR: *(& www.stoppenendoorgaan.nl Hoewel aan de totstandkoming van deze uitgave de uiterste zorg is besteed, aan- vaarden de auteur en uitgever geen aansprakelijkheid voor eventuele fouten en onvolkomenheden, noch voor de directe of indirecte gevolgen hiervan. Niets uit deze uitgave mag zonder voorafgaande schriftelijke toestemming van de uitgever worden openbaar gemaakt of verveelvoudigd, waaronder begrepen het reproduceren door middel van druk, o+set, fotokopie of micro%lm of in enige digitale, elektronische, optische of andere vorm of (en dit geldt zonodig in aanvul- ling op het auteursrecht) het reproduceren (I) ten behoeve van een onderneming, organisatie of instelling of (II) voor eigen oefening, studie of gebruik welk(e) niet strikt privé van aard is. stoppen& doorgaan Over het leven na topsport Margriet de Schutter It doesn’t matter how many times you get knocked down but how many times you get up – Vince Lombardi Vincent !omas ‘Vince’ Lombardi ("" juni "#"$ - $ september "#%&) was een succesvol American Football coach in de jaren ‘'&. -

Salt Lake City 2002
SALT LAKE CITY 2002 The Games of the XIX Winter Olympiad. February 8-24, 2002. Salt Lake City, USA. 1 ALPINE SKIING MEN Downhill: 2.Lasse Kjus (Norway) Giant slalom: 3.Lasse Kjus (Norway) Giant slalom: 1.Stephen Eberharter (Austria) Super-G: 2.Stephen Eberharter (Austria) Downhill: 3.Stephen Eberharter (Austria) Combined 1.Kjetil Andre Aamodt (Norway) 2 Combined: 3.Benjamin Raich (Austria) Slalom: 3.Benjamin Raich (Austria) Super-G 1.Kjetil Andre Aamodt (Norway) 3 WOMEN Downhill 2.Isolde Kostner (Italy) Combined: 1.Janica Kostelic (Croatia) Super-G: 2.Janica Kostelic (Croatia) 4 Giant slalom 1.Janica Kostelic (Croatia) 3.Sonja Nef (Switzerland) 15.Brigitte Obermoser (Austria) Slalom 1.Janica Kostelic (Croatia) 5 BIATHLON MEN 20 km individual: 1.Ole Einar Bjorndalen (Norway) 10 km sprint: 1.Ole Einar Bjorndalen (Norway) 12.5 km pursuit: 1.Ole Einar Bjorndalen (Norway) 4 x 7.5 km: 1.Norway (Ole Einar Bjorndalen) 4 x 7.5 km 1.Norway (Halvard Hanevold) 2.Germany 6 BOBSLEIGH Four-man 1.Germany (Andre Lange, Kevin Kuske) 7 CROSS-COUNTRY SKIING MEN 2 x 10 km pursuit 1-2.Thomas Alsgaard (Norway) 15 km classical 1.Andrus Veerpalu (Estonia) 8 50 km classical 2.Andrus Veerpalu (Estonia) 4 x 10 km 1.Norway (Thomas Alsgaard) 9 WOMEN 2 x 5 km pursuit: 2.Katerina Neumannova (Czech Republic) 15 km freestyle mass start: 2.Katerina Neumannova (Czech Republic) 30 km classical: 2.Stefania Belmondo (Italy) 10 km classical: 3.Stefania Belmondo (Italy) 15 km freestyle mass start 1.Stefania Belmondo (Italy) 10 4 x 5 km 2.Norway (Marit Bjorgen) 11 CURLING Men -

Salt Lake City 2002
SALT LAKE CITY 2002 The Games of the XIX Winter Olympiad. February 8-24, 2002. Salt Lake City, USA. 1 ALPINE SKIING MEN Super-G 1.Kjetil Andre Aamodt (Norway) Combined: 1.Kjetil Andre Aamodt (Norway) Downhill: 2.Lasse Kjus (Norway) Giant slalom: 3.Lasse Kjus (Norway) Downhill: 3.Stephan Eberharter (Austria) Combined: 3.Benjamin Raich (Austria) Super-G: 2.Stephan Eberharter (Austria) Slalom: 3.Benjamin Raich (Austria) Giant slalom: 1.Stephan Eberharter (Austria) 2 WOMEN Downhill 2.Isolde Kostner (Italy) Combined: 1.Janica Kostelic (Croatia) Super-G: 2.Janica Kostelic (Croatia) Giant slalom: 1.Janica Kostelic (Croatia) Slalom: 1.Janica Kostelic (Croatia) Giant slalom: 3.Sonja Nef (Switzerland) 3 BIATHLON MEN 20 km individual: 1.Ole Einar Bjorndalen (Norway) 10 km sprint: 1.Ole Einar Bjorndalen (Norway) 12.5 km pursuit: 1.Ole Einar Bjorndalen (Norway) 4 x 7.5 km: 1.Norway (Ole Einar Bjorndalen) 4 x 7.5 km: 1.Norway (Halvard Hanevold) 4 WOMEN 10 km pursuit 3.Irina Nikulchina (Bulgaria) 15 km individual: 3.Magdalena Forsberg (Sweden) 7.5 km sprint: 3.Magdalena Forsberg (Sweden) 5 BOBSLEIGH Two-man 1.Christoph Langen / Markus Zimmermann (Germany) Four-man 1.Germany (Andre Lange, Kevin Kuske) 6 CROSS-COUNTRY SKIING MEN 15 km classical 1.Andrus Veerpalu (Estonia) 50 km classical: 2.Andrus Veerpalu (Estonia) 2 x 10 km pursuit: 1-2.Thomas Alsgaard (Norway) 4 x 10 km: 1.Norway (Thomas Alsgaard) 7 WOMEN 2 x 5 km pursuit: 2.Katerina Neumannova (Czech Republic) 15 km freestyle mass start: 2.Katerina Neumannova (Czech Republic) 10 km classical: 3.Stefania -

Olympische Kwalificatiewedstijden
ISU WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2017 FEBRUARY, 25 and 26, 2017; OLYMPIC OVAL - CALGARY Table of contents page 1. World records, World records Jun. ,Track records and Championship records 2, 3 2. Country records 4 3. List of the World Champions Sprint and the numbers 2 and 3 5 – 8 4. Medals Classification World Sprint Championships Ladies and Men 9 - 11 5. Personal Best Ladies and Men 12, 13 6. Results in previous World Championships Sprint 14, 15 7. Intermediate times and Lap times WR, TR and CR 16 22. February 2017 Statistical Documentation compiled by Ronald Kruit and Alex Dumas (Netherlands) ISU WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2017 FEBRUARY, 25 and 26, 2017; OLYMPIC OVAL - CALGARY Records Ladies 500 meter World record 36,36 Sang-Hwa (KOR) Salt Lake City 16-11-2013 World record Jun. 37,81 Sang-Hwa Lee (KOR) Salt Lake City 10-03-2007 Track record 36,74 Sang-Hwa Lee (KOR) Calgary 09-11-2013 Championship record 36,94 Jing Yu (CHN) Calgary 29-01-2012 1000 meter World record 1.12,18 Brittany Bowe (USA) Salt Lake City 22-11-2015 World record Jun. 1.14,95 Hyun-Yung Kim (KOR) Salt Lake City 17-11-2013 Track record 1.12,51 Heather Bergsma (USA) Calgary 14-11-2015 Championship record 1.12,68 Christine Nesbitt (CAN) Calgary 28-01-2012 Points Sprint Combination World record 147.735 Heather Bergsma (USA) Calgary 19/20-1-2013 (37,12 – 1.13,09 – 37,42 – 1.13,30) World record Jun. 152.470 Karolina Erbanová (CZE) Calgary 28/29-1-2012 (38,17 – 1.16,97 – 38,11 – 1.15,41) Track record see World record Championship record 148.015 Heather Bergsma (USA) Salt Lake City 26/27-1-2013 (37,31 – 1.13,74 – 37,24 – 1.13,19) 2 ISU WORLD SPRINT SPEED SKATING CHAMPIONSHIPS 2017 FEBRUARY, 25 and 26, 2017; OLYMPIC OVAL - CALGARY Records Men 500 meter World record 33,98 Pavel Kulizhnikov (RUS) Salt Lake City 20-11-2015 World record Jun. -

THE ARUP JOURNAL Editorial: Tel: +44 (0)20 7755 3828 Fax: 44 (0)20 7755 3716 E-Mail: [email protected]
Vol 37 No 2, (212002). Ecfrtor: David J Brown Art Editor and Designer: Desmond Wyeth FCSO: Deputy Editor: Karen Svensson THE ARUP JOURNAL Editorial: tel: +44 (0)20 7755 3828 fax: 44 (0)20 7755 3716 e-mail: [email protected] Published by Arup, 13 Fitzroy Street. London W1T 480, UK. Tel: +44 (0)20 7636 1531 Fax: +44 (0)20 7580 3924 e-mail: [email protected] www.arup.com Arup is a global organisation of designers. It has a constantly evolving skills base, and works for local and international clients throughout the world. We shape a better world Front cover: the Acton Peninsula redevelopment, Canberra (pp3-11) Photo: John Gollings Photography Back cover: The Imperial War Museum, London: Stage 3 (pp 42-47) Photo: Andrew Putler 3 12 18 NMA and Druk White Hang Tuah ACE AIATSIS: Lotus School, Platform: The Acton Ladakh, Delivering a Peninsula Northern India new offshore redevelopment, Jim Fleming product Canberra Rory McGowan Gordon Jackson Pippa Connolly Dorothea Richter Brian Raine Jonathan Rose The virtuosic architectural concept for the New Since 1997 a voluntary team of architects and To improve the economics of platform installation Museum of Australia and the Aboriginal and Torres engineers from Arup Associates and Arup has and the practicalities of supporting topsides Islander Institute of Studies in Canberra required worked on this school, which will eventually cater process facilities, Arup developed the ACE range both an innovative structural approach by Arup, for 750 pupils, in a remote corner of Northern of self-installing, moveable platforms for extracting and the use of the alliancing concept between India. -

Dachkonstruktion Speedskating Oval for the 2010 Winter Olympics in V
14. Internationales Holzbau-Forum 08 Speedskating Oval for the 2010 Winter Olympics in Vancouver, Canada | P. Fast 1 Eisschnelllaufhalle der 2010 Winter Olympics, Vancou- ver - Dachkonstruktion Speedskating Oval for the 2010 Winter Olympics in Vancouver, Canada Stadio per pattinaggio di velocità 2010, giochi olimpici invernali Vancouver - Kanada Halle du patinage de vitesse des Jeux olympiques d’hiver 2010 Vancouver – Canada Paul Fast P. Eng., Struct.Eng., P.E. LEED® AP Fast + Epp structural engineers Vancouver, Canada 14. Internationales Holzbau-Forum 08 2 Speedskating Oval for the 2010 Winter Olympics in Vancouver, Canada | P. Fast 14. Internationales Holzbau-Forum 08 Speedskating Oval for the 2010 Winter Olympics in Vancouver, Canada | P. Fast 3 Speedskating Oval for the 2010 Winter Olympics in Vancouver, Canada 1. Introduction When the IOC awarded the 2010 Winter Olympics to Vancouver,B.C., architectural at- tention immediately turned to the building that would host the long track speed skating venue. Speed skating ovals are unique buildings that provide opportunity for striking ar- chitectural- structural expression. Operating on a lean budget, VANOC (Vancouver Olympic Organizing Committee) decided to offload financial risk for the facility by committing the fixed sum of $60M CAD to the neighbouring City of Richmond, who would then assume ownership of the building and responsibility for the remainder of the $178M construction budget. Following an interna- tional request for proposals, Cannon Design Architects was appointed the prime consult- ant with Fast + Epp structural engineers the structural sub-consultant for the roof struc- ture. Figure 1: Richmond Speed Skating Oval, Richmond, British Columbia, Canada 2. Building Description The speed skating oval is a roughly 100m wide by 200m long building with a total roof area including overhangs of 23,700 square metres. -

19-03 Carlson Center Ice Rink Replacement
FNSB CAPITAL IMPROVEMENT PROGRAM 2019 Project Nomination Form Nominations will be accepted from August 12 to October 11. Please fill out the nomination form as completely as possible. If a section does not apply to the project you are nominating, please leave that section blank. Please attach add itional relevant information to this nomination packet as appropriate. There is no limit to the number of projects that can be submitted. Completed nomination forms can be submitted: In person at: By mail to: Fairbanks North Star Borough Fairbanks North Star Borough Attn: Mayor's Office Attn: Capital Improvement Program 907 Terminal Street PO Box 71267 Fa irbanks, AK 99701 Fairbanks, AK 99707 NOMINATOR'S NAME: j t:.. v r T ~8 ~Et,_,=-v $" ORGANIZATION (IF APPLI CABLE) : _____________________ AFFECTED DEPARTMENT: _ ___.~_ A_,,,e._ t,_~-"--"/1/___ ?_ ~_.;v,_ '/_/;:_; _,C,______ _ ___ _ PHONE : I 'jtJ 7 ) JY7 ... 9111 Project Scope/Description: ~6e' -:- A,.,. e -z./ C/7 / /o/ _,,. ,,., ,;-,..,,r ~r:, ,,. e I J- fu:,rr ~ ,,, ///'-</Pf f {~z-y) 77? -- ? 'I z 3 - "f'P~ {_ p Io ) f/~ ~ - ~ tJ 9 I - C ca. _j/4) ,'//,/,t-;M ,7 ei /'t,~ - q //I{ c/'I 'CA- " ~ .,_.,_ Learn mare at: www.fnsb.us/CIP Page 1 of 11 FNSB CAPITAL IMPROVEMENT PROGRAM SAFETY AND CODE COMPLIANCE 1. Does the project reduce or eliminate a health or safety risk? □ Yes D No Please explain: /1?~-,,,.,...u-ee?? ~/?"~ (!)/ 4'v' C ""? /-/ " --v ;5 If N ~ A/V "!? tt,v>-c!Y"'7 4~/&'V ~ ~ 1·" '7A./ q J7.