DOCSLIB.ORG

Rotation of Axes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Rotation of Axes Rotation of Axes The point P is the same in both the xy and xy coordinate systems. The point can be represented in the xy plane as xr cos and yrsin The point can be represented in the xy plane as xr cos and yr sin Using the sum of angles identities from trigonometry gives us ... xrcos yrsin rrcos cos sin sin rrcos sin sin cos xycos sin xysin cos Substituting x and y into the general form Ax22 Bxy Cy Dx Ey F 0 gives: Axcos y sin2 Bx cos y sin x sin y cos Cxsin y cos2 Dx cos y sin Ex sin y cos F 0 Expanding the factors gives: Ax 22cos 2 xy cos sin y 22 sin B x2222cos sin xy cos xy sin y cos sin Cx22sin 2 xy cos sin y 2 cos 2 Dxcos y sin Ex sin y cos F 0 Collecting the terms yields: xA22 cos B cos sin C sin 2 xy Bcos22 sin 2 A C cos sin yA22sin B cos sin C cos 2 xDcos E sin y D sin E cos F 0 The double angle identities cos 2 cos22 sin and sin 2 2cos sin allow us to rewrite the xy term. xA22 cos B cos sin C sin 2 xy Bcos2 A C sin 2 yA22sin B cos sin C cos 2 xDcos E sin y D sin E cos F 0 The general form can be written as Ax 22 Bxy Cy Dx Ey F 0 where AA cos22 B cos sin C sin BB cos 2 AC sin 2 CA sin22 B cos sin C cos DD cos E sin ED sin E cos FF The goal is to find the angle of rotation Some people will find it easier to use such that B 0 . 1 1 B BACcos2 sin 2 0 tan BACcos2 sin 2 2 A C cos 2 AC We don't because it is possible that A C and you might get division by zero. sin 2 B A C cot 2 We can avoid this by using the inverse B cotangent function. We know that B will 1 AC 2cot never be zero since the whole point is to B eliminate the xy term. 1 1 A C Also, the range of the inverse cotangent is cot 2 B between 0E and 180E, so 02180 , which means that 090 . While it is possible to get an angle using this formula, it is usually easier to draw a triangle with 2θ as the angle and use the half-angle identities to find the values for sin θ and cos θ. 1cos2 1cos2 cos2 and sin2 2 2 The discriminant, BAC2 4 , can be used to determine the type of conic section. The discriminant is not affected by the rotation, so you can use the original coefficients or the new ones after the rotation. The discriminant does not detect the degenerate cases. If BAC2 40, the conic is a circle or an ellipse. If BAC2 40, the conic is a parabola. If BAC2 40, the conic is a hyperbola. Example Problem 27xxyy22 270 57 282 25 x 285 22 y 287 0 2 The discriminant is BAC2 4 2 70 4 2 7 5 7 280 280 0 Since the discriminant is 0, this is going to be a parabola. AC27 57 37 3 cot 2 B 270 270210 1210 If you need to know the angle, then tan1 32.31153324 23 But you don't need to know the angle to get rid of the xy term. 3 Draw a triangle so that cot 2 and use it to determine the 210 values for the cosine and sine using the half angle identities. Use the positive values for cos and sin since is an acute angle. 1cos2 13/75 5 cos2 cos 227 7 1cos2 13/72 2 sin2 sin 227 7 Make the substitutions into the formulas above. A 2755 270221 57 1020100 7777 7 310210 B 270 777 27 57 6 6 0 C 2 7221 2 7055 5 7 4 20 25 49 7777 77 5 2 D 28 2 2 5 77 28 5 2 2 2810 10 10 4 392 77 E 28 2 2 52 28 5 2 2 5 77 282 2 10 5 2 10 196 77 F 28 7 The new equation in the xy plane is 00xxyy22 49 392 x 196 y 2870. 777 7 Multiplying everything by gives yxy2 8440. 49 Notice that the discriminant is still zero. Graph before rotation. BAC22404010 If you put general equation into standard form by completing the square, you get yyx2 484 yy2 44844 x yx282 1 2 yx2421 Same graph after rotation by 32.3 . This is a parabola with a vertex at 1, 2 , opening along the positive x axis, with a focal length of 2. That puts the focus at 1, 2 and the directrix at x 3. sin 2 7 2 Use tan to get the correct cos 57 5 angle on the rotated axes. tan1 2 5 32.3.
Load more

Recommended publications
  • Transformation of Axes
    19 Chapter 2 Transformation of Axes 2.1 Transformation of Coordinates It sometimes happens that the choice of axes at the beginning of the solution of a problem does not lead to the simplest form of the equation. By a proper transformation of axes an equation may be simplified. This may be accom- plished in two steps, one called translation of axes, the other rotation of axes. 2.1.1 Translation of axes Let ox and oy be the original axes and let o0x0 and o0y0 be the new axes, parallel respectively to the old ones. Also, let o0(h, k) referred to the origin of new axes. Let P be any point in the plane, and let its coordinates referred to the old axes be (x, y) and referred to the new axes be (x0y0) . To determine x and y in terms of x0, y0, h and x = h + x0 y = k + y0 20 Chapter 2. Transformation of Axes these equations represent the equations of translation and hence, the coeffi- cients of the first degree terms are vanish. 2.1.2 Rotation of axes Let ox and oy be the original axes and ox0 and oy0 the new axes. 0 is the origin for each set of axes. Let the angle x0 ox through which the axes have been rotated be represented by q. Let P be any point in the plane, and let its coordinates referred to the old axes be (x, y) and referred to the new axes be (x0, y0), To determine x and y in terms of x0, y0 and q : x = OM = ON − MN = x0 cos q − y0 sin q and y = MP = MM0 + M0P = NN0 + M0P = x0 sin q + y0 cos q 2.1.
    [Show full text]
  • Analysis of a Hyperbolic Paraboloid Surface with Curved Edges
    ANALYSIS,, OF A HYPERBOLIC PARABOLOID by Carlos Alberto Asturias Theai1 submitted to the Graduate Faculty of the Virginia Polytechnic Institute in candidacy for the degree of MASTER OF SCIENCE in Structural Engineering December 17, 1965 Blacksburg, Virginia · -2- TABLE OF CONTENTS Page I. INTRODUCTION ••••••••••••••••••••••••••••••••••• 5 11. OBJECTIVE •••••••••••••••••••••••••••••••••••••• 8 Ill. HISTORICAL BACKGROUND • ••••••••••••••••••••••••• 9 IV. NOTATION ••••••••••••••••••••••••••••••••••••••• 10 v. METHOD OF ANALYSIS • •••••••••••••••••••••••••••• 12 VI. FORMULATION OF THE METHOD • ••••••••••••••••••••• 15 VII. THEORETICAL INVESTIGATION • ••••••••••••••••••••• 24 A. DEVELOPMENT OF EQUATIONS • •••••••••••••• 24 B. ILLUSTRATIVE EXAMPLE • •••••••••••••••••• 37 VIII. EXPERIMENTAL WORK • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • 50 A. DESCRIPTION OF THE MODEL ••••••••••••••• 50 B. TEST SET UP •••••••••••••••••••••••••••• 53 IX. TEST RESULTS AND CONCLUSIONS • •••••••••••••••••• 61 X. BIBLIOGRAPHY ••••••••••••••••••••••••••••••••••• 65 XI. ACKNOWLEDGMENT • •••••••••••••••••••••••••••••••• 67 XII. VITA • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • 68 -3- LIST OF FIGURES Page FIGURE I. HYPERBOLIC PARABOLOID TYPES ••••••••••••• 7 FIGURE II. DIFFERENTIAL ELEMENT .................... 13 FIGURE III. AXES .................................... 36 FIGURE IV. DIMENSIONS •••••••••••••••••••••••••••••• 36 FIGURE v. STRESSES ., • 0 ••••••••••••••••••••••••••••• 44 FIGURE VI. STRESSES •••••••••••••••••••••••••••
    [Show full text]
  • APPENDIX E Rotation and the General Second-Degree Equation
    APPENDIX E Rotation and the General Second-Degree Equation Rotation of Axes • Invariants Under Rotation y y′ Rotation of Axes In Section 9.1, you learned that equations of conics with axes parallel to one of the coordinate axes can be written in the general form 2 1 2 1 1 1 5 x′ Ax Cy Dx Ey F 0. Horizontal or vertical axes θ Here you will study the equations of conics whose axes are rotated so that they are not x parallel to the x-axis or the y-axis. The general equation for such conics contains an xy-term. Ax2 1 Bxy 1 Cy2 1 Dx 1 Ey 1 F 5 0 Equation in xy-plane To eliminate this xy-term, you can use a procedure called rotation of axes. You want to rotate the x- and y-axes until they are parallel to the axes of the conic. (The rotated axes are denoted as the x9-axis and the y9-axis, as shown in Figure E.1.) After the After rotation of the x- and y-axes counter- rotation has been accomplished, the equation of the conic in the new x9y9-plane will clockwise through an angle u, the rotated have the form axes are denoted as the x9-axis and y9-axis. A9sx9d2 1 C9sy9d2 1 D9x9 1 E9y9 1 F9 5 0. Equation in x9y9-plane Figure E.1 Because this equation has no x9y9-term, you can obtain a standard form by complet- ing the square. The following theorem identifies how much to rotate the axes to eliminate an xy-term and also the equations for determining the new coefficients A9, C9, D9, E9, and F9.
    [Show full text]
  • Rotation of Axes
    ROTATION OF AXES ■■ For a discussion of conic sections, see In precalculus or calculus you may have studied conic sections with equations of the form Calculus, Early Transcendentals, Sixth Edition, Section 10.5. Ax2 ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 Here we show that the general second-degree equation 1 Ax2 ϩ Bxy ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 can be analyzed by rotating the axes so as to eliminate the term Bxy. In Figure 1 the x and y axes have been rotated about the origin through an acute angle ␪ to produce the X and Y axes. Thus, a given point P has coordinates ͑x, y͒ in the first coor- dinate system and ͑X, Y͒ in the new coordinate system. To see how X and Y are related to x and y we observe from Figure 2 that X ෇ r cos ␾ Y ෇ r sin ␾ x ෇ r cos͑␪ ϩ ␾͒ y ෇ r sin͑␪ ϩ ␾͒ y y Y P(x, y) Y P(X, Y) P X Y X r y ˙ ¨ ¨ 0 x 0 x X x FIGURE 1 FIGURE 2 The addition formula for the cosine function then gives x ෇ r cos͑␪ ϩ ␾͒ ෇ r͑cos ␪ cos ␾ Ϫ sin ␪ sin ␾͒ ෇ ͑r cos ␾͒ cos ␪ Ϫ ͑r sin ␾͒ sin ␪ ෇ ⌾ cos ␪ Ϫ Y sin ␪ A similar computation gives y in terms of X and Y and so we have the following formulas: 2 x ෇ X cos ␪ Ϫ Y sin ␪ y ෇ X sin ␪ ϩ Y cos ␪ By solving Equations 2 for X and Y we obtain 3 X ෇ x cos ␪ ϩ y sin ␪ Y ෇ Ϫx sin ␪ ϩ y cos ␪ EXAMPLE 1 If the axes are rotated through 60Њ, find the XY-coordinates of the point whose xy-coordinates are ͑2, 6͒.
    [Show full text]
  • Rotation of Axes 1 Rotation of Axes
    Rotation of Axes 1 Rotation of Axes At the beginning of Chapter 5 we stated that all equations of the form Ax2 + Bxy + Cy2 + Dx + Ey + F =0 represented a conic section, which might possibly be degenerate. We saw in Section 5.2 that the graph of the quadratic equation Ax2 + Cy2 + Dx + Ey + F =0 is a parabola when A =0orC = 0, that is, when AC = 0. In Section 5.3 we found that the graph is an ellipse if AC > 0, and in Section 5.4 we saw that the graph is a hyperbola when AC < 0. So we have classified the situation when B = 0. Degenerate situations can occur; for example, the quadratic equation x2 + y2 + 1 = 0 has no solutions, and the graph of x2 − y2 = 0 is not a hyperbola, but the pair of lines with equations y = x. But excepting this type of situation, we have categorized the graphs of all the quadratic equations with B =0. When B =6 0, a rotation can be performed to bring the conic into a form that will allow us to compare it with one that is in standard position. To set up the discussion, letusfirstsupposethatasetofxy-coordinate axes has been rotated about the origin by an angle θ, where 0 <θ<π=2, to form a new set ofx ^y^-axes, as shown in Figure 1(a). We would like to determine the coordinates for a point P in the plane relative to the two coordinate systems. y y yˆ yˆ P(x, y) P(xˆˆ, y) P(x, y) P(xˆˆ, y) r xˆ r xˆ B f B u u A x A x (a) (b) Figure 1 2 CHAPTER 5 Conic Sections, Polar Coordinates, and Parametric Equations First introduce a new pair of variables r and φ to represent, respectively, the distance from P to the origin and the angle formed by thex ^-axis and the line connecting the origin to P , as shown in Figure 1(b).
    [Show full text]
  • Rotation of Axes
    ROTATION OF AXES ■■ For a discussion of conic sections, see In precalculus or calculus you may have studied conic sections with equations of the form Review of Conic Sections. Ax2 ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 Here we show that the general second-degree equation 1 Ax2 ϩ Bxy ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 can be analyzed by rotating the axes so as to eliminate the term Bxy. In Figure 1 the x and y axes have been rotated about the origin through an acute angle ␪ to produce the X and Y axes. Thus, a given point P has coordinates ͑x, y͒ in the first coor- dinate system and ͑X, Y͒ in the new coordinate system. To see how X and Y are related to x and y we observe from Figure 2 that X ෇ r cos ␾ Y ෇ r sin ␾ x ෇ r cos͑␪ ϩ ␾͒ y ෇ r sin͑␪ ϩ ␾͒ y y Y P(x, y) Y P(X, Y) P X Y X r y ˙ ¨ ¨ 0 x 0 x X x FIGURE 1 FIGURE 2 The addition formula for the cosine function then gives x ෇ r cos͑␪ ϩ ␾͒ ෇ r͑cos ␪ cos ␾ Ϫ sin ␪ sin ␾͒ ෇ ͑r cos ␾͒ cos ␪ Ϫ ͑r sin ␾͒ sin ␪ ෇ ⌾ cos ␪ Ϫ Y sin ␪ A similar computation gives y in terms of X and Y and so we have the following formulas: 2 x ෇ X cos ␪ Ϫ Y sin ␪ y ෇ X sin ␪ ϩ Y cos ␪ By solving Equations 2 for X and Y we obtain 3 X ෇ x cos ␪ ϩ y sin ␪ Y ෇ Ϫx sin ␪ ϩ y cos ␪ EXAMPLE 1 If the axes are rotated through 60Њ, find the XY-coordinates of the point whose xy-coordinates are ͑2, 6͒.
    [Show full text]
  • Rotation of Axes 2 ROTATION of AXES
    Rotation of Axes 2 I ROTATION OF AXES Rotation of Axes GGGGGGGGGGGGGGGG L For a discussion of conic sections, see In precalculus or calculus you may have studied conic sections with equations of the Calculus, Fourth Edition, Section 11.6 form Calculus, Early Transcendentals, Fourth Edition, Section 10.6 Ax2 ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 Here we show that the general second-degree equation 1 Ax2 ϩ Bxy ϩ Cy2 ϩ Dx ϩ Ey ϩ F ෇ 0 can be analyzed by rotating the axes so as to eliminate the term Bxy. In Figure 1 the x and y axes have been rotated about the origin through an acute angle ␪ to produce the X and Y axes. Thus, a given point P has coordinates ͑x, y͒ in the first coordinate system and ͑X, Y͒ in the new coordinate system. To see how X and Y are related to x and y we observe from Figure 2 that X ෇ r cos ␾ Y ෇ r sin ␾ x ෇ r cos͑␪ ϩ ␾͒ y ෇ r sin͑␪ ϩ ␾͒ y y Y P(x, y) Y P(X, Y) P X Y X r y ˙ ¨ ¨ 0 x 0 x X x FIGURE 1 FIGURE 2 The addition formula for the cosine function then gives x ෇ r cos͑␪ ϩ ␾͒ ෇ r͑cos ␪ cos ␾ Ϫ sin ␪ sin ␾͒ ෇ ͑r cos ␾͒ cos ␪ Ϫ ͑r sin ␾͒ sin ␪ ෇ ⌾ cos ␪ Ϫ Y sin ␪ A similar computation gives y in terms of X and Y and so we have the following formulas: 2 x ෇ X cos ␪ Ϫ Y sin ␪ y ෇ X sin ␪ ϩ Y cos ␪ By solving Equations 2 for X and Y we obtain 3 X ෇ x cos ␪ ϩ y sin ␪ Y ෇ Ϫx sin ␪ ϩ y cos ␪ ROTATION OF AXES N 3 EXAMPLE 1 If the axes are rotated through 60Њ, find the XY-coordinates of the point whose xy-coordinates are ͑2, 6͒.
    [Show full text]
  • Rotation of Conics Practice.Tst
    Precalculus Rotation of Conics Identify the equation without completing the square. 1) 4y2 - 3x + 2y = 0 1) A) hyperbola B) ellipse C) parabola D) not a conic Determine the appropriate rotation formulas to use so that the new equation contains no xy -term. 2) x2 + 2xy + y2 - 8x + 8y = 0 2) 2 2 A) x = (xʹ - yʹ) and y = (xʹ + yʹ) 2 2 1 3 3 1 B) x = xʹ - yʹ and y = xʹ + yʹ 2 2 2 2 2 + 2 2 - 2 2 - 2 2 + 2 C) x = xʹ - yʹ and y = xʹ + yʹ 2 2 2 2 D) x = -yʹ and y = xʹ Rotate the axes so that the new equation contains no xy -term. Discuss the new equation. 3) x2 + 2xy + y2 - 8x + 8y = 0 3) A) θ = 36.9° B) θ = 45° xʹ2 yʹ2 yʹ2 = -42xʹ + = 1 4 4 parabola ellipse vertex at (0, 0) center (0, 0) focus at (- 2, 0) major axis is xʹ-axis vertices at (±2, 0) C) θ = 45° D) θ = 36.9° xʹ2 = -42yʹ xʹ2 yʹ2 + = 1 parabola 4 2 vertex at (0, 0) ellipse focus at (0, - 2) center (0, 0) major axis is xʹ-axis vertices at (±2, 0) Identify the equation without applying a rotation of axes. 4) x2 + 12xy + 36y2 - 4x + 3y - 10 = 0 4) A) ellipse B) parabola C) hyperbola D) not a conic 5) 2x2 + 6xy + 9y2 - 3x + 2y + 6 = 0 5) A) hyperbola B) ellipse C) parabola D) not a conic 6) 3x2 + 12xy + 2y2 - 3x - 2y + 5 = 0 6) A) ellipse B) hyperbola C) parabola D) not a conic Precalculus 7) x2 + 3xy - 2y2 + 4x - 4y + 1 = 0 7) A) hyperbola B) parabola C) ellipse D) not a conic 8) 5x2 - 3xy + 2y2 + 3x + 4y + 2 = 0 8) A) hyperbola B) ellipse C) parabola D) not a conic Rotate the axes so that the new equation contains no xy -term.
    [Show full text]
  • Supplement on Rotation of Axes
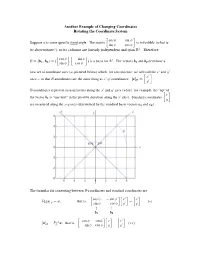
    Another Example of Changing Coordinates Rotating the Coordinate System cos9 sin 9 Suppose 9 is some specific fixed angle. The matrix is invertible ( what is ”sin 9cos 9 • its determinant? ), so its columns are linearly independent and span ‘#. Therefore cos9 sin 9 U œÖ,,ß ×œÖ ß × is a basis for ‘ #. The vectors , and , determine a "# ”sin 9 •”cos 9 • " # new set of coordinate axes (as pictured below) which, for convenience, we will call the Bw and C w w w w B axes so that U-coordinates are the same thing as B- C coordinates: Ò BÓU œ . ”Cw • U-coordinates represent measurements along the Bw and C w axes (where, for example, the “tip” of B the vector , is “one unit” in the positive direction along the Bw axis). Standard coordinates " ”C • are measured along the BC- axes (determined by the standard basis vectors /" and / # ÑÞ The formulas for converting between U-coordinates and standard coordinates are cos 9sin 9 Bw B T ÒB Ó œ B , that is, œ Ð‡Ñ U U ”sin9 cos 9 •”•”•Cw C Å Å ," , # cos 9sin 9 B B w ÒÓœTB" B , that is, œ Ї‡Ñ U U ”sin 9cos 9 •”•”• C C w You may have seen these “rotation of axes” formula written out, in precalculus or calculus, in a harder to remember form: BœBw cos99 Cw sin BœBw cos 99 C sin Ð‡Ñ and Ї‡Ñ œ C œ Bw sin 99 Cw cosœ Cw œ B sin 99 C cos In the future, to get these formulas you just need to remember how to write a rotation matrix and the formula TU ÒB ÓU œ B .
    [Show full text]
  • Math 142 Fall 2000 Rotation of Axes in Section 11.4, We Found That Every
    Math 142 Fall 2000 Rotation of Axes In section 11.4, we found that every equation of the form (1) Ax2 + Cy2 + Dx + Ey + F =0, with A and C not both 0, can be transformed by completing the square into a standard equation of a translated conic section. Thus, the graph of this equation is either a parabola, ellipse, or hyperbola with axes parallel to the x and y-axes (there is also the possibility that there is no graph or the graph is a “degenerate” conic: a point, a line, or a pair of lines). In this section, we will discuss the equation of a conic section which is rotated by an angle θ, so the axes are no longer parallel to the x and y-axes. To study rotated conics, we first look at the relationship between the axes of the conic and the x and y-axes. If we label the axes of the conic by u and v, then we can describe the conic in the usual way in the uv-coordinate system with an equation of the form (2) au2 + cv2 + du + ev + f =0 Label the axis in the first quadrant by u, so that the u-axis is obtained by rotating the x-axis through an angle θ, with 0 <θ<π/2 (see Figure 1). Likewise, the v-axis is obtained by rotating the y-axis through the angle θ.NowifP is any point with usual polar coordinates (r, α), then the polar coordinates of P in the uv system are (r, α − θ) (again, see Figure 1).
    [Show full text]
  • 1 Chapter 4 Coordinate Geometry in Three Dimensions
    1 CHAPTER 4 COORDINATE GEOMETRY IN THREE DIMENSIONS 4.1 Introduction Various geometrical figures in three-dimensional space can be described relative to a set of mutually orthogonal axes O x, Oy, Oz, and a point can be represented by a set of rectangular coordinates ( x, y, z ). The point can also be represented by cylindrical coordinates ( ρ , φ , z) or spherical coordinates ( r , θ , φ ), which were described in Chapter 3. In this chapter, we are concerned mostly with ( x, y, z ). The rectangular axes are usually chosen so that when you look down the z-axis towards the xy -plane, the y-axis is 90 o counterclockwise from the x-axis. Such a set is called a right-handed set. A left-handed set is possible, and may be useful under some circumstances, but, unless stated otherwise, it is assumed that the axes chosen in this chapter are right-handed. An equation connecting x, y and z, such as f (x, y,z) = 0 4.1.1 or z = z(x, y) 4.1.2 describes a two-dimensional surface in three-dimensional space. A line (which need be neither straight nor two-dimensional) can be described as the intersection of two surfaces, and hence a line or curve in three-dimensional coordinate geometry is described by two equations, such as f (x, y, z) = 0 4.1.3 and g (x, y, z) = 0. 4.1.4 In two-dimensional geometry, a single equation describes some sort of a plane curve. For example, y2 = 4 qx 4.1.5 describes a parabola.
    [Show full text]
  • Conic Sections and Polar Coordinates
    4100 AWL/Thomas_ch10p685-745 8/25/04 2:34 PM Page 685 Chapter CONIC SECTIONS 10 AND POLAR COORDINATES OVERVIEW In this chapter we give geometric definitions of parabolas, ellipses, and hyperbolas and derive their standard equations. These curves are called conic sections, or conics, and model the paths traveled by planets, satellites, and other bodies whose motions are driven by inverse square forces. In Chapter 13 we will see that once the path of a mov- ing body is known to be a conic, we immediately have information about the body’s veloc- ity and the force that drives it. Planetary motion is best described with the help of polar co- ordinates, so we also investigate curves, derivatives, and integrals in this new coordinate system. 10.1 Conic Sections and Quadratic Equations In Chapter 1 we defined a circle as the set of points in a plane whose distance from some fixed center point is a constant radius value. If the center is (h, k) and the radius is a, the standard equation for the circle is sx - hd2 + s y - kd2 = a2 . It is an example of a conic section, which are the curves formed by cutting a double cone with a plane (Figure 10.1); hence the name conic section. We now describe parabolas, ellipses, and hyperbolas as the graphs of quadratic equa- tions in the coordinate plane. Parabolas DEFINITIONS Parabola, Focus, Directrix A set that consists of all the points in a plane equidistant from a given fixed point and a given fixed line in the plane is a parabola.
    [Show full text]