DOCSLIB.ORG

Insights Into Cosmological Structure Formation with Machine Learning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Insights Into Cosmological Structure Formation with Machine Learning Insights into cosmological structure formation with machine learning Luisa Lucie-Smith Submitted for the degree of Doctor of Philosophy Department of Physics and Astronomy University College London Supervisors: Examiners: Prof. Hiranya V. Peiris Prof. Benjamin Wandelt Prof. Andrew Pontzen Prof. Ofer Lahav 31st of October, 2019 I, Luisa Lucie-Smith, confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. 1 Abstract Our modern understanding of cosmological structure formation posits that small matter density fluctuations present in the early Universe, as traced by the cosmic microwave background, grow via gravitational instability to form extended haloes of dark matter. A theoretical understanding of the structure, evolution and formation of dark matter haloes is an essential step towards unravelling the intricate connection between halo and galaxy formation, needed to test our cosmological model against data from upcoming galaxy surveys. Physical understanding of the process of dark matter halo formation is made difficult by the highly non-linear nature of the haloes’ evolution. I describe a new approach to gain physical insight into cosmological structure formation based on machine learning. This approach combines the ability of machine learning algorithms to learn non-linear relationships, with techniques that enable us to physically interpret the learnt mapping. I describe applications of the method, with the aim of investigating which aspects of the early universe density field impact the later formation of dark matter haloes. First I present a case where the process of halo formation is turned into a binary classification problem; the algorithm predicts whether or not dark matter ‘particles’ in the initial conditions of a simulation will collapse into haloes of a given mass range. Second, I present its generalization to regression, where the algorithm infers the final mass of the halo to which each particle will later belong. I show that the initial tidal shear does not play a significant role compared to the initial density field in establishing final halo masses. Finally, I demonstrate that extending the framework to deep learning algorithms such as convolutional neural networks allows us to explore connections between the early universe and late time haloes beyond those studied by existing analytic approximations of halo collapse. 2 Impact Statement This thesis presents a new approach based on machine learning, aimed at deepening our under- standing of the formation of dark matter haloes in the Universe. Our goal is to understand what information is learnt by the machine learning algorithm about the underlying connection between the early universe and the late-time dark matter haloes in cosmological simulations; this differs from common approaches where machine learning is utilized as a black-box tool to obtain fast and automated mappings. Our method led to a re-interpretation of the existing understanding of halo formation over the last decades, in particular in relation to the role of the tidal shear tensor in establishing the final mass of dark matter haloes (Chapters3 & 4). This work achieved academic impact through two scientific publications, cited by independent researchers around the world, and over ten professional presentations, including invited talks, at international conferences for broad and specialized audiences from the cosmology and machine learning communities. Thanks to the broad applicability of our method, there has been an upsurge of interest in the community to apply our method to other aspects of dark matter haloes, leading to new international collaborations for the PhD candidate. The advances in machine learning presented in this thesis can be directly applied to industrial and commercial applications of artificial intelligence (AI). One of the key problems faced in the AI community is the issue of interpretability; without a deeper understanding of how deep learning algorithms make their predictions, we cannot trust AI tools in scientific, industrial and commercial applications. Our methods are specifically designed to turn black-box algorithms into interpretable ones, allowing one to better understand the complex systems these algorithms describe. This is particularly relevant for convolutional neural networks (Chapter5), which are used extensively in industry. In addition to being interpretable, our deep learning architecture allows for broader 3 applicability to three-dimensional data sets than conventional architectures applied to 2D images. Finally, this thesis points toward a new branch of machine learning research known as knowledge extraction (Chapter6), where deep learning algorithms are constructed in a manner that allows for the discovery of fundamental properties of the underlying data sets. This work has initiated an international collaboration of experts in the fields of brain sciences, computational psychiatry, crime sciences and physics, as well as Google DeepMind. We expect this collaboration to expedite progress in the ability of humans to extract knowledge from machine learning algorithms. 4 Acknowledgements First, I owe my deepest gratitude to my amazing supervisors, Hiranya Peiris and Andrew Pontzen, for investing an infinite amount of time in making me a better researcher. Thank you for always being there for me, for being extremely attentive mentors, for the endless support and understanding at difficult times and for sharing with me your scientific expertise and insights. Working with you and being your student has been a privilege. Thank you to all the other brilliant cosmologists I was lucky enough to collaborate with – Nina Roth, Michelle Lochner, Brian Nord, Risa Wechsler and Susmita Adhikari – for the all the help in the fun projects carried out together. I am extremely grateful to Edd Edmondson and John Deacon for solving all my IT problems in no time. Special thanks also go to Corentin Cadou, Martin Rey and Sam Witte for proof reading parts of this thesis. Thank you to all the friends I have made at UCL for the laughs, pub trips and occasional trips to Borderline. Special thoughts go to Felix Priestley for listening to extensive monologues starting with ‘about me now’, Arthur Loureiro for keeping me up to date on Brazilian politics, Arianna Sorba for always having an answer to my questions, Niall Jeffrey for that magnum I still owe him, Martin Rey for our morning coffees and paper discussions, Keir Rogers for the wisest advices on surviving a PhD, Michelle Lochner for buying all the rounds at the pub, Andreu Font-Ribera for rigorously drinking only half pints at the pub, Roger Wesson for still not accepting that I won, Jonathan Braden for laughing at the words baryons and stars, Davide Gualdi for excellent coffees in his office, Will Hartley for always reminding us to never work on photo-z and Sam Witte, for introducing me to my newest big loves, Jim Croce and pad thai. Thank you to all the very good friends I made during my time at Fermilab, especially for the numerous pitchers of Aperol spritz drank at the village pub. Special thanks go to Antonella Palmese for making me feel at home and Federico Speranza for our shared passion for country music and for grating parmigiano on my pasta. Thanks to all the Italian 5 songwriters that kept me company during long hours of work, Francesco De Gregori, Lucio Battisti, Brunori Sas and Tiromancino, and to Pyotr Ilyich Tchaikovsky, for the most productive hours of thesis writing. A big thank you and all my love goes to my family. Thanks to my dad, for teaching me special relativity when I was way too young to understand it, my brother, for always being there for all of us, and my sister for the “sclero times” together. Thank you to Martina for being my best friend. My deepest love goes to my mum, Antonella, for being the strongest and most inspiring woman I know on this planet and for all the love and support she has given me. Thank you for your efforts in trying to learn about my research, although I know you still think I work on black holes. I dedicate this thesis to you, cocca. 6 Contents 1 Introduction 19 1.1 The Universe....................................... 19 1.1.1 General relativity................................. 20 1.1.2 The energy content................................ 23 1.1.3 Expansion history................................. 24 1.2 Seeds of cosmic structures................................ 26 1.2.1 The cosmic microwave background....................... 27 1.2.2 Inflation...................................... 29 1.3 Cosmological structure formation............................ 32 1.3.1 Linear growth................................... 33 1.3.2 Non-linear growth................................ 38 1.3.3 Spherical collapse model............................. 38 1.3.4 Press-Schechter Formalism............................ 40 1.4 Numerical simulations.................................. 43 1.4.1 The GADGET code................................. 46 1.4.2 Initial conditions................................. 47 1.4.3 Finding dark matter haloes........................... 48 1.5 Outline of the thesis................................... 49 2 Method 51 2.1 Machine learning algorithms............................... 51 2.1.1 Decision trees................................... 54 7 2.1.2 Ensembles of decision trees........................... 56 2.1.3 Feature importances............................... 60 2.2 Deep learning algorithms...............................
Load more

Recommended publications
  • Annual Report to Industry Canada Covering The
    Annual Report to Industry Canada Covering the Objectives, Activities and Finances for the period August 1, 2008 to July 31, 2009 and Statement of Objectives for Next Year and the Future Perimeter Institute for Theoretical Physics 31 Caroline Street North Waterloo, Ontario N2L 2Y5 Table of Contents Pages Period A. August 1, 2008 to July 31, 2009 Objectives, Activities and Finances 2-52 Statement of Objectives, Introduction Objectives 1-12 with Related Activities and Achievements Financial Statements, Expenditures, Criteria and Investment Strategy Period B. August 1, 2009 and Beyond Statement of Objectives for Next Year and Future 53-54 1 Statement of Objectives Introduction In 2008-9, the Institute achieved many important objectives of its mandate, which is to advance pure research in specific areas of theoretical physics, and to provide high quality outreach programs that educate and inspire the Canadian public, particularly young people, about the importance of basic research, discovery and innovation. Full details are provided in the body of the report below, but it is worth highlighting several major milestones. These include: In October 2008, Prof. Neil Turok officially became Director of Perimeter Institute. Dr. Turok brings outstanding credentials both as a scientist and as a visionary leader, with the ability and ambition to position PI among the best theoretical physics research institutes in the world. Throughout the last year, Perimeter Institute‘s growing reputation and targeted recruitment activities led to an increased number of scientific visitors, and rapid growth of its research community. Chart 1. Growth of PI scientific staff and associated researchers since inception, 2001-2009.
    [Show full text]
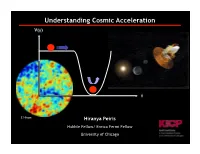
  • Understanding Cosmic Acceleration: Connecting Theory and Observation
    Understanding Cosmic Acceleration V(!) ! E Hivon Hiranya Peiris Hubble Fellow/ Enrico Fermi Fellow University of Chicago #OMPOSITIONOFAND+ECosmic HistoryY%VENTS$ UR/ INGTHE%CosmicVOLUTIONOFTHE5 MysteryNIVERSE presentpresent energy energy Y density "7totTOT = 1(k=0)K density DAR RADIATION KENER dark energy YDENSIT DARK G (73%) DARKMATTER Y G ENERGY dark matter DARK MA(23.6%)TTER TIONOFENER WHITEWELLUNDERSTOOD DARKNESSPROPORTIONALTOPOORUNDERSTANDING BARYONS BARbaryonsYONS AC (4.4%) FR !42 !33 !22 !16 !12 Fractional Energy Density 10 s 10 s 10 s 10 s 10 s 1 sec 380 kyr 14 Gyr ~1015 GeV SCALEFACTimeTOR ~1 MeV ~0.2 MeV 4IME TS TS TS TS TS TSEC TKYR T'YR Y Y Planck GUT Y T=100 TeV nucleosynthesis Y IES TION TS EOUT DIAL ORS TIONS G TION TION Z T Energy THESIS symmetry (ILC XA 100) MA EN EE WNOF ESTHESIS V IMOR GENERATEOBSERVABLE IT OR ELER ALTHEOR TIONS EF SIGNATURESINTHE#-" EAKSYMMETR EIONIZA INOFR Y% OMBINA R E6 EAKDO #X ONASYMMETR SIC W '54SYMMETR IMELINEOF EFFWR Y Y EC TUR O NUCLEOSYN ), * +E R 4 PLANCKENER Generation BR TR TURBA UC PH Cosmic Microwave NEUTR OUSTICOSCILLA BAR TIONOFPR ER A AC STR of primordial ELEC non-linear growth of P 44 LIMITOFACC Background Emitted perturbations perturbations: GENER ES carries signature of signature on CMB TUR GENERATIONOFGRAVITYWAVES INITIALDENSITYPERTURBATIONS acoustic#-"%MITT oscillationsED NON LINEARSTR andUCTUR EIMPARTS #!0-!0OBSERVES#-" ANDINITIALDENSITYPERTURBATIONS GROWIMPARTINGFLUCTUATIONS CARIESSIGNATUREOFACOUSTIC SIGNATUREON#-"THROUGH *throughEFFWRITESUPANDGR weakADUATES WHICHSEEDSTRUCTUREFORMATION
    [Show full text]
  • Annual Review 2011/12
    UCL DEPARTMENT OF PHYSICS AND ASTRONOMY PHYSICS AND ASTRONOMY 2011–12 ANNUAL REVIEW PHYSICS AND ASTRONOMY ANNUAL REVIEW 2011–12 Contents Welcome It is an honour to write this WELCOME 1 introduction standing, to misquote Newton, on the shoulders of giants. COMMUNITY FOCUS 3 Jonathan Tennyson finished his Teaching Lowdown 4 tenure as Head of Department in September 2011 and so the majority Student Accolades 4 of the material contained in this Outstanding PhD Theses Published 5 Review records achievements under his leadership. In addition, Tony Career Profiles 6 Harker is currently acting as Head of Science in Action 8 Department in many matters and will continue to do so until October 2012. Alumni Matters 9 This is due to my on-going commitments with the ATLAS experiment on the ACADEMIC SHOWCASE 11 Large Hadron Collider (LHC) at CERN. Staff Accolades 12 I currently spend a large amount of my time in Geneva and I am very grateful Academic Appointments 14 to both Tony and Jonathan, as well as to other members of staff for helping Doctor of Philosophy (PhD) 15 to make this transition a success. In Portrait of Dr Phil Jones 16 particular I would also like to thank Hilary Wigmore as Departmental Manager and Raman Prinja as the new Director of RESEARCH SPOTLIGHT 17 Teaching for their continued support. Atomic, Molecular, Optical and Position Physics (AMOPP) 19 High Energy Physics (HEP) 21 “Success in such long- Condensed Matter and term, high-impact projects Materials Physics (CMMP) 25 requires sustained vision Astrophysics (Astro) 29 and dedicated work by Biological Physics (BioP) 33 excellent scientists over Research Statistics 35 many years.” Staff Snapshot 38 Underpinning this success is the outstanding quality of scientific research and education within the Department.
    [Show full text]
  • UNIVERSITY COLLEGE LONDON Understanding the Distribution Of
    UNIVERSITY COLLEGE LONDON Department of Physics & Astronomy Understanding the distribution of gas in the Universe Teresita Suarez´ Noguez Thesis presented for the Degree of Doctor of Philosophy Supervisors: Examiners: Dr Andrew Pontzen Prof. Richard Ellis Prof. Hiranya V. Peiris Dr James Bolton January 25, 2018 Declaration I, Teresita Suarez´ Noguez , declare that the thesis entitled Understanding the distribution of gas in the Universe and the work presented in the thesis are both my own, and have been generated by me as the result of my own original research. I confirm the thesis is based on work done by myself jointly with others, I have made clear exactly what was done by others and what I have contributed myself. This work has not been submitted for any other degree at UCL or any other University. London, January 25, 2018 Teresita Suarez´ Noguez Understanding the distribution of gas in the Universe Teresita Suarez´ Noguez Abstract The distribution of gas in the Universe can be observed in absorption in the spectra of quasars. However, interpreting the spectra requires comparison to physical models which map the distribution, temperatures and ionisation states of the gas. First, I focused on understanding the presence of outflowing cold gas around galaxies. I performed numerical simulations to study how outflows, launched from a central galaxy undergoing starbursts, affect the circumgalactic medium. I model an outflow as a rapidly moving bubble of gas above the disk and analyse its evolution. I sampled a distribution of parameters with a grid of two-dimensional hydrodynamical simulations –with and without– radiative cooling, assuming primordial gas composition.
    [Show full text]
  • The Practical Use of Cosmic Shear As a Probe of Gravity
    The Practical use of Cosmic Shear as a Probe of Gravity Donnacha Kirk Thesis submitted for the Degree of Doctor of Philosophy of the University College London Department of Physics & Astronomy UNIVERSITY COLLEGE LONDON April 2011 I, Donnacha Kirk, confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. Specifically: • The work on luminosity functions and red galaxy fractions in section 2.7 was done by Dr. Michael Schneider (then at Durham) as part of our collaboration on the paper Kirk et al. (2010). • The work in chapters 3 & 4 is my contribution to, and will form the substantial part of, papers in preparation with collaborators Prof. Rachel Bean and Istvan Lazslo at Cornell University. The MG effect on the linear growth function was computed by Istvan Lazslo. • The Great08 section of chapter 6 draws on my contributions to the Great08 Handbook (Bridle et al. 2009), Great08 Results Paper (Bridle et al. 2010a) and Great10 Handbook (Kitching et al. 2010). To Mum and Dad, for everything. Boyle. ... an’ it blowed, an’ blowed – blew is the right word, Joxer, but blowed is what the sailors use... Joxer. Aw, it’s a darlin’ word, a daarlin’ word. Boyle. An’, as it blowed an’ blowed, I often looked up at the sky an’ assed meself the question – what is the stars, what is the stars? Voice of Coal Vendor. Any blocks, coal-blocks; blocks, coal-blocks! Joxer. Ah, that’s the question, that’s the question – what is the stars? Boyle.
    [Show full text]
  • Sum of the Masses of the Milky Way and M31: a Likelihood-Free Inference Approach Pablo Lemos, Niall Jeffrey, Lorne Whiteway, Ofer Lahav, Noam I
    Sum of the masses of the Milky Way and M31: A likelihood-free inference approach Pablo Lemos, Niall Jeffrey, Lorne Whiteway, Ofer Lahav, Noam I. Libeskind, Yehuda Hoffman To cite this version: Pablo Lemos, Niall Jeffrey, Lorne Whiteway, Ofer Lahav, Noam I. Libeskind, et al.. Sum ofthe masses of the Milky Way and M31: A likelihood-free inference approach. Phys.Rev.D, 2021, 103 (2), pp.023009. 10.1103/PhysRevD.103.023009. hal-02999468 HAL Id: hal-02999468 https://hal.archives-ouvertes.fr/hal-02999468 Submitted on 26 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. PHYSICAL REVIEW D 103, 023009 (2021) Sum of the masses of the Milky Way and M31: A likelihood-free inference approach Pablo Lemos ,1,* Niall Jeffrey ,2,1 Lorne Whiteway ,1 Ofer Lahav,1 Noam Libeskind I,3,4 and Yehuda Hoffman5 1Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, United Kingdom 2Laboratoire de Physique de l’Ecole Normale Sup´erieure, ENS, Universit´e PSL, CNRS, Sorbonne Universit´e, Universit´e de Paris, Paris, France 3Leibniz-Institut
    [Show full text]
  • List of Participants
    COSMO 2014 August 25-29, 2014 International Conference on Particle Physics and Cosmology, 2014 Chicago, IL http://cosmo2014.uchicago.edu/ LIST OF PARTICIPANTS http://kicp.uchicago.edu/ http://www.nsf.gov/ http://www.kavlifoundation.org/ http://www.uchicago.edu/ The 18th annual International Conference on Particle Physics and Cosmology (COSMO 2014) will be held in Chicago on August 25 29, 2014. The meeting is being hosted by the Kavli Institute for Cosmological Physics (KICP) at the University of Chicago, and will be held at the University of Chicago's Gleacher Center in downtown Chicago. Plenary Speakers Nima Arkani-Hamed Laura Baudis Stefano Borgani Institute for Advanced Study University of Zurich Astronomical Observatory of Trieste Kiwoon Choi Ryan Foley Wendy Freedman Institute for Basic Science (IBS) University of Illinois, Urbana-Champaign Carnegie Observatories Daniel Green Catherine Heymans Justin Khoury CITA University of Edinburgh University of Pennsylvania Will Kinney Lloyd Knox John Kovac University at Buffalo, SUNY UC Davis Harvard University Andrei Linde Nikhil Padmanabhan Hiranya Peiris Stanford University Yale University University College London Sarah Shandera Eva Silverstein Tracy Slatyer Pennsylvania State University Stanford University Massachusetts Institute of Technology Mark Trodden Neal Weiner University of Pennsylvania New York University International Steering Committee Vernon Barger Daniel Baumann John Beacom University of Wisconsin-Madison Cambridge University Ohio State University David Caldwell Jonathan Ellis
    [Show full text]
  • Curriculum Vitae
    CURRICULUM VITAE FULL NAME: George Petros EFSTATHIOU NATIONALITY: British DATE OF BIRTH: 2nd Sept 1955 QUALIFICATIONS Dates Academic Institution Degree 10/73 to 7/76 Keble College, Oxford. B.A. in Physics 10/76 to 9/79 Department of Physics, Ph.D. in Astronomy Durham University EMPLOYMENT Dates Academic Institution Position 10/79 to 9/80 Astronomy Department, Postdoctoral Research Assistant University of California, Berkeley, U.S.A. 10/80 to 9/84 Institute of Astronomy, Postdoctoral Research Assistant Cambridge. 10/84 to 9/87 Institute of Astronomy, Senior Assistant in Research Cambridge. 10/87 to 9/88 Institute of Astronomy, Assistant Director of Research Cambridge. 10/88 to 9/97 Department of Physics, Savilian Professor of Astronomy Oxford. 10/88 to 9/94 Department of Physics, Head of Astrophysics Oxford. 10/97 to present Institute of Astronomy, Professor of Astrophysics (1909) Cambridge. 10/04 to 9/08 Institute of Astronomy, Director Cambridge. 10/08 to present Kavli Institute for Cosmology, Director Cambridge. PROFESSIONAL SOCIETIES Fellow of the Royal Society since 1994 Fellow of the Instite of Physics since 1995 Fellow of the Royal Astronomical Society 1983-2010 Member of the International Astronomical Union since 1986 Associate of the Canadian Institute of Advanced Research since 1986 1 AWARDS/Fellowships/Major Lectures 1973 Exhibition Keble College Oxford. 1975 Johnson Memorial Prize University of Oxford. 1977 McGraw-Hill Research Prize University of Durham. 1980 Junior Research Fellowship King’s College, Cambridge. 1984 Senior Research Fellowship King’s College, Cambridge. 1990 Maxwell Medal & Prize Institute of Physics. 1990 Vainu Bappu Prize Astronomical Society of India.
    [Show full text]
  • Prof. Ofer Lahav: Curriculum Vitae
    Prof. Ofer Lahav: Curriculum Vitae Department of Physics and Astronomy Phone: +44 (0) 20 7679 3473 University College London (UCL) Mobile: +44 (0) 7738848597 Gower Street E-mail: [email protected] London WC1E 6BT Web: www.homepages.ucl.ac.uk/~ucapola/ United Kingdom Home address: 3 Monks Close Canterbury CT2 7ET Current position Perren Chair of Astronomy Department of Physics & Astronomy, UCL Other current roles Co-Chair of the Science Committee of the international Dark Energy Survey Vice-Dean for Research, Faculty of Mathematical and Physical Sciences, UCL Holder of a European Research Council Advanced Grant (2012-2017) Date and Place of Birth: 5 April 1959; Tiberias, Israel Citizenship: Israeli and British Education University of Cambridge: Astronomy Ph.D., 1988 (Supervisors: Prof. G. Efstathiou and Prof. D. Lynden-Bell) Ben-Gurion University: Physics M.Sc., 1985 (Supervisor: Prof. J. Bekenstein) Tel-Aviv University: Physics B.Sc., 1980 Positions 2004- Perren Professor of Astronomy, UCL 2011- Vice-Dean for Research, Faculty of Mathematical and Physical Sciences, UCL 2004-2011 Head of Astrophysics, Physics & Astronomy Department, UCL 2000-2003 Reader in Cosmology, Institute of Astronomy, Cambridge University 1998-1999 on leave as Associate Professor, the Hebrew University, Jerusalem 1990-2000 Member of staff, Institute of Astronomy, Cambridge University (Senior Assistant in Research, Assistant Director of Research, Lecturer) 1989 Post-doctoral Fellow, Institute for Advanced Study, Princeton 1988-2003 Research Fellow (1988-91) and then
    [Show full text]
  • Physics and Astronomy ANNUAL REVIEW 2013–14 UCL DEPARTMENT of PHYSICS and ASTRONOMY
    Physics and Astronomy ANNUAL REVIEW 2013–14 UCL DEPARTMENT OF PHYSICS AND ASTRONOMY PHYSICS AND ASTRONOMY ANNUAL REVIEW 2014–15 1 WELCOME Physics and Astronomy ANNUAL REVIEW 2013–14 Contents Welcome 1 WELCOME The year 2014 ended with the The tragic death of Bruce Swinyard 2 COMMUNITY FOCUS announcement of the Research in May 2015 was a great loss, and Excellence Framework results, an our thoughts are with his family. A full 3 Teaching Lowdown important exercise in which all UK obituary appears on page 13. universities are assessed on their 4 Student Accolades research activities, and on which Several members of the department 6 Students in Action funding allocations are then based. received prizes in 2014: Benjamin The Department formed the bulk of Joachimi and Ofer Lahav won awards 8 Career Profile UCL’s ‘Physics’ submission, with major from the Royal Astronomical society, contributions also from our colleagues in 9 Alumni Matters as did the Herschel and Cassini teams the London Centre for Nanotechnology which have several UCL members. 10 Science in Action and in the Mullard Space Science David Walker won the IoP Optics and Laboratory. 11 ACADEMIC SHOWCASE Photonics prize, Angela Occhiogrosso and Jennifer Chan won the faculty 12 Staff News postgraduate research and taught 13 Obituary course prizes, respectively. Steve …the department is Fossey won the UCL Communications 14 Staff Accolades “ and Culture award (remember the 15 Portrait of… strong and confdent. supernova discovery in Messier 82 from We will meet these the last review!). Matthew Wing won 16 Reserch Degrees the Friedrich Wilhelm Bessel Research challenges together, and Award from the Humboldt Foundation, 17 RESEARCH SPOTLIGHT continue to prosper.
    [Show full text]
  • The Royal Astronomical Society Since 2010
    ROYAL ASTRONOMICAL SOCIETY Burlington House, Piccadilly London W1J 0BQ, UK T: 020 7734 4582 F: 020 7494 0166 [email protected] www.ras.org.uk Registered Charity 226545 ELECTION OF OFFICERS AND COUNCIL – 2015 Biographical Notes of Candidates President Elect OFER LAHAV (A) BSc (Tel-Aviv U) , MSc (Ben-Gurion U), PhD (Cambridge U), FRAS, FintP, Perren Professor of Astronomy, University College London (since 2004), formerly Head of UCL Astrophysics (2004-2011), formerly member of staff at the Institute of Astronomy Cambridge U (1990-2003), currently Vice-Dean (Research) of UCL’s Faculty of Mathematical and Physical Sciences, holder of a European Research Council Advanced Grant, co-chair of the international Dark Energy Survey Science Committee and chair of DES:UK, co-authored over 200 refereed papers, supervised 18 PhD students, served as RAS Council member (2009-2012), Vice-President (2010-2012; chaired the Awards and International committees), editor of MNRAS (2006-2008), Awarded the RAS 2014 Gerald Whitrow Lecture, and the 2008 RAS Group Award to the 2dFGRS team. Research interests: cosmological probes of dark matter and dark energy, large galaxy surveys, statistical methods, history of astronomy. Statement: I am keen to enhance the RAS profile and its connection to the UK Research Councils, and other societies (e.g. RS, IoP, EAS, IAU), as well as to explore funding opportunities through the EU and charity organizations, and to run a fund-raising campaign for RAS@200. The RAS would be strengthened by a closer connection between the Astronomy and Geophysics sections of the RAS, to be achieved in the first instance by initiating meetings with a common interest, e.g.
    [Show full text]
  • NL#153 July/August
    AAAS Publication for the members N of the Americanewsletter Astronomical Society July/August 2010, Issue 153 CONTENTS President's Column Debra Meloy Elmegreen, [email protected] 2 th From the Moon over Miami, palm trees, and a riverwalk set the perfect scene for our 216 meeting, a typically intimate summer gathering with about 800 attendees. Kudos and thanks to Kevin and Executive Office his Marvel-ous staff for another smooth and well-executed gathering. It was all the more special because of meeting jointly with the Solar Physics Division, which happens every three years. It is nice when the smaller divisions are able to overlap with the general meeting, to foster more interactions among astronomers who work in a variety of fields. Dramatic results from new 3 missions such as Herschel, Hinode and SDO, WISE, CoRot, Cassini-Huygens observations of Journals Update Titan, CMB observations from the South Pole, progress on ALMA, and solar tales from SPD Hale prize winner Marcia Neugebauer and Harvey prize winner Brian Welsch were among the many exciting presentations. 4 Three newly funded opportunities were announced: the Doxsey Award for thesis-presenting Council Actions graduate students to travel to the AAS, the Lancelot Berkeley Prize for meritorious recently published research to be presented at the AAS, and the Kavli Award to a distinguished plenary AAS speaker, as discussed elsewhere in this Newsletter. 5 I was thinking about what makes AAS meetings special. We gather for the science, of course; the general meetings provide opportunities to get a firsthand update on key advances, which help Secretary's Corner inform not only our research but also our teaching.
    [Show full text]