English, Lyn & Watters, James Mathematical Modelling with 9-Year
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
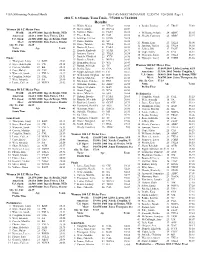
2004 Olympic Trials Results
USA Swimming-National Meets Hy-Tek's MEET MANAGER 12:55 PM 1/26/2005 Page 1 2004 U. S. Olympic Team Trials - 7/7/2004 to 7/14/2004 Results 13 Walsh, Mason 19 VTAC 26.08 8 Benko, Lindsay 27 TROJ 55.69 Women 50 LC Meter Free 15 Silver, Emily 18 NOVA 26.09 World: 24.13W 2000 Inge de Bruijn, NED 16 Vollmer, Dana 16 FAST 26.12 9 Williams, Stefanie 24 ABSC 55.95 American: 24.63A 2000 Dara Torres, USA 17 Price, Keiko 25 CAL 26.16 10 Shealy, Courtney 26 ABSC 55.97 18 Jennings, Emilee 15 KING 26.18 U.S. Open: 24.50O 2000 Inge de Bruijn, NED 19 Radke, Katrina 33 SC 26.22 Meet: 24.90M 2000 Dara Torres, Stanfor 11 Phenix, Erin 23 TXLA 56.00 20 Stone, Tammie 28 TXLA 26.23 Oly. Tr. Cut: 26.39 12 Jamison, Tanica 22 TXLA 56.02 21 Boutwell, Lacey 21 PASA 26.29 Name Age Team 13 Jeffrey, Rhi 17 FAST 56.09 22 Harada, Kimberly 23 STAR 26.33 Finals Time 14 Cope, Haley 25 CAJ 56.11 23 Jamison, Tanica 22 TXLA 26.34 15 Wanezek, Sarah 21 TXLA 56.19 24 Daniels, Elizabeth 22 JCCS 26.36 Finals 16 Nymeyer, Lacey 18 FORD 56.56 25 Boncher, Brooke 21 NOVA 26.42 1 Thompson, Jenny 31 BAD 25.02 26 Hernandez, Sarah 19 WA 26.43 2 Joyce, Kara Lynn 18 CW 25.11 27 Bastak, Ashleigh 22 TC 26.47 Women 100 LC Meter Free 3 Correia, Maritza 22 BA 25.15 28 Denby, Kara 18 CSA 26.50 World: 53.66W 2004 Libby Lenton, AUS 4 Cope, Haley 25 CAJ 25.22 29 Ripple Johnston, Shell 23 ES 26.51 American: 53.99A 2002 Natalie Coughlin, U 5 Wanezek, Sarah 21 TXLA 25.27 29 Medendorp, Meghan 22 IST 26.51 U.S. -

Code De Conduite Pour Le Water Polo
HistoFINA SWIMMING MEDALLISTS AND STATISTICS AT OLYMPIC GAMES Last updated in November, 2016 (After the Rio 2016 Olympic Games) Fédération Internationale de Natation Ch. De Bellevue 24a/24b – 1005 Lausanne – Switzerland TEL: (41-21) 310 47 10 – FAX: (41-21) 312 66 10 – E-mail: [email protected] Website: www.fina.org Copyright FINA, Lausanne 2013 In memory of Jean-Louis Meuret CONTENTS OLYMPIC GAMES Swimming – 1896-2012 Introduction 3 Olympic Games dates, sites, number of victories by National Federations (NF) and on the podiums 4 1896 – 2016 – From Athens to Rio 6 Olympic Gold Medals & Olympic Champions by Country 21 MEN’S EVENTS – Podiums and statistics 22 WOMEN’S EVENTS – Podiums and statistics 82 FINA Members and Country Codes 136 2 Introduction In the following study you will find the statistics of the swimming events at the Olympic Games held since 1896 (under the umbrella of FINA since 1912) as well as the podiums and number of medals obtained by National Federation. You will also find the standings of the first three places in all events for men and women at the Olympic Games followed by several classifications which are listed either by the number of titles or medals by swimmer or National Federation. It should be noted that these standings only have an historical aim but no sport signification because the comparison between the achievements of swimmers of different generations is always unfair for several reasons: 1. The period of time. The Olympic Games were not organised in 1916, 1940 and 1944 2. The evolution of the programme. -

1/4/2004 Piscina Olímpica Encantada T
Untitled 1/5/04 10:24 AM Licensed to Natacion Fernando Delgado Hy-Tek's Meet Manager II WINTER TRAINING MEET - 1/4/2004 PISCINA OLÍMPICA ENCANTADA TRUJILLO ALTO, PUERTO RICO Results Event 1 Women Open 200 LC Meter Medley Relay =============================================================================== MEET RECORD: * 2:07.03 1/5/2003 SYRACUSE, SYRACUSE- R Wrede, J Jonusaitis, E McDonough, C Jansen School Seed Finals =============================================================================== 1 NOTRE DAME SWIMMING 'A' 2:00.78 2:05.38* 2 NOTRE DAME SWIMMING 'B' 2:05.85 2:06.39* 3 SYRACUSE ORANGEMEN 'A' 2:04.13 2:07.59 4 YALE 'A' 1:59.10 2:09.30 5 ST'S. JOHNS UNIVERSITY 'A' 1:58.35 2:09.94 6 NADADORES SANTURCE 'A' 2:11.51 2:12.48 7 SETON HALL UNIVERSITY 'A' 2:07.98 2:13.43 8 YALE 'B' 2:03.60 2:13.86 9 ST'S. JOHNS UNIVERSITY 'B' 2:01.50 2:14.43 10 GEORGETOWN SWIMMING 'A' 2:10.33 2:15.81 11 ST'S. JOHNS UNIVERSITY 'C' 2:05.00 2:16.53 12 BRANDIES UNIVERSITY 'A' 3:11.00 2:17.50 13 YALE 'C' 2:05.70 2:17.73 14 SETON HALL UNIVERSITY 'B' 2:15.64 2:20.05 15 NADADORES SANTURCE 'B' 2:15.87 2:20.21 16 NOTRE DAME SWIMMING 'C' 2:10.77 2:22.08 17 GEORGETOWN SWIMMING 'B' 2:14.55 2:22.68 18 MONTCLAIR STATE UNIVERSITY 'A' 2:07.30 2:29.65 19 BRANDIES UNIVERSITY 'B' 3:20.00 2:29.75 Event 2 Men Open 200 LC Meter Medley Relay =============================================================================== MEET RECORD: * 1:53.79 1/5/2003 YALE UNIVERSITY, YALE- School Seed Finals =============================================================================== 1 SETON HALL UNIVERSITY 'A' 1:44.09 1:51.80* 2 YALE 'A' 1:44.30 1:53.18* 3 SYRACUSE ORANGEMEN 'A' 1:46.22 1:54.65 4 NADADORES SANTURCE 'A' 1:58.39 1:55.65 5 NADADORES SANTURCE 'B' 2:02.01 1:56.01 6 YALE 'B' 1:49.70 1:56.66 7 ST'S. -

Analysis of Stroke Rates in Freestyle Events at 2000 Olympics
ANALYSIS OF STROKE RATES IN FREESTYLE EVENTS AT 2000 OLYMPICS By David Pyne & Cassie Trewin Department of Physiology, Australian Institute of Sport The aim of this article is to examine the patterns of stroke rates of successful swimmers during the 2000 Sydney Olympic Games. Stroke rates of swimmers in the Final (top 8 swimmers) of selected Freestyle events were taken from the Competition Analysis of the 2000 Olympic Games (courtesy of the Biomechanics Department, Australian Institute of Sport). The stroke rates for each 25, 50 or 100m race split and placing in the 50, 100, 200 and 400 m freestyle events were collated. The interesting questions are … Were there differences in stroke rates between the sprint (50 and 100m) and middle-distance (200 and 400m) events? Were there any differences in stroke rates between the Men’s and Women’s events? How much variation in stroke rate was evident between swimmers in the same event? And how much difference was observed between first and last lap stroke rates compared to the average for the event for each individual swimmer. The individual and mean stroke rates for each of the finalists in the 50, 100, 200 and 400 Freestyle events are presented in Table 1. Statistical analysis (data not shown) indicated that there were no significant correlations between average stroke rate on any lap and final placing. The only exception was the Women’s 400m Freestyle where the placegetters had a significantly higher average stroke rate over the race than those swimmers finishing outside the medals. This indicates that there is considerable variation in stroke rate between different swimmers at the Olympic level. -

Record Revolution Underway Canadian Olympic Trials
CANADIAN OLYMPIC TRIALS RECORD REVOLUTION UNDERWAY $ 4.95 USA NUMBER 258 www.swimnews.com MAY-JUNE 2000 $ 4.95 CAN CANADIANCANADIAN RECORDRECORD SETTERSETTER RICKRICK SAYSAY O'NEILLO'NEILL ANDAND THORPETHORPE RULERULE AUSTRALIANAUSTRALIAN TRIALSTRIALS 2 SWIMNEWS / MAY-JUNE 2000 SWIMNEWS CONTENTS MAY-JUNE 2000 N. J. Thierry, Editor & Publisher CONSECUTIVE NUMBER 258 VOLUME 27, NUMBER 5 Marco Chiesa, Business Manager Karin Helmstaedt, International Editor FEATURES Russ Ewald, Sunland, USA Editor Paul Quinlan, Australian Editor 14 Australian Olympic Trials / Nationals Nick Thierry Cecil Colwin, Ottawa, Features Editor Anita Smale, Copy Editor Aussies Have Strongest Olympic Team in 40 Years Feature Writers George Block, San Antonio, USA 17 Personality: Ian Thorpe Ian Hanson Nikki Dryden, Calgary Knows No Fear, Knows No Barriers or Limits Katharine Dunn, Halifax Wayne Goldsmith, Australia 18 Personality: Susan O’Neill Ian Hanson Anita Lonsbrough, England Oldest Record Falls International Statistical Support Group: Jorge Aguado, Argentina 16-17 Poster: Geoff Huegill Marco Chiesa Rumen Atanasov, Bulgaria Chaker Belhadj, Tunisia 22 Canadian Olympic Trials Katherine Dunn Young-Ryul Cho, Korea Rick Say Betters 20-Year-Old 400 Free Record Szabolcs Fodor, Hungary Gerd Heydn, Germany Three Canadian Records Tumble Franck Jensen, Denmark Berth Johansson, Sweden 23 Qualify for Individual Events and 13 as Relay Alternates Daniel Pichon / Michel Salles, France Hans Peter Sick, Germany 25 Personality: Michael Mintenko Nikki Dryden Juan Antonio Sierra, Spain Neville Smith, South Africa Success at Age 24 Fratisek Stochl, Czech Republic 26 Trends Katherine Dunn Nelson Vargas, Mexico Janusz Wasko, Poland Older, Wiser, and Faster Sumire Watanabe, Japan Computer programs for TAG, World Rankings 27 Nikki’s Diary Nikki Dryden developed by EveryWare Development Corporation. -

2020 U.S. Olympic Team Trials - Swimming 1 Media Guidelines & Information Usaswimming.Org/Trials L @Usaswimming L @Usaswimmingnews L #Swimtrials21
2020 U.S. Olympic Team Trials - Swimming 1 Media Guidelines & Information usaswimming.org/trials l @USASwimming l @USASwimmingNews l #SwimTrials21 Facility Address Media Seating CHI Health Center Omaha USA Swimming will provide seating charts for tabled media in the competition 455 N. 10th Street venue. Overflow (non-tabled) media seating is available in section 102 and 103. Omaha, NE 68102 Seating in the media work room will not be assigned. COVID-19 Guidelines Internet Getty Images All credentialed, on-site media must adhere to the COVID-19 health and safety Wireless internet access will be available throughout the various media work areas. protocols listed at www.usaswimming.org/trials. Media members must receive a Ethernet connections will be available in the Media Seating Area (tables only), 2020 U.S. Olympic Team Trials - Swimming Media Guide COVID-19 PCR test 3-6 days before picking up their credentials in Omaha. select photographer locations and the Media Work Room. usaswimming.org/trials l @USASwimming l @USASwimmingNews l #SwimTrials21 Credentials Photographer Guidelines Competition Details Media credential pick-up will be located at the media entrance of the CHI Health Steven Currie will again serve as the photo chief for the U.S. Olympic Team Trials - Center Omaha. The entrance is located at the back of the building (east side of the Swimming. He will assist and coordinate locations for all photographers in Omaha. Wave I Dates: June 4-7, 2021 building), adjacent to Parking Lot A. This will be the media entrance throughout the Complete guidelines will be distributed to all credentialed photographers prior to Wave II Dates: June 13-20, 2021 me11-1et. -

Men's Olympic Swimming Sinks While Title IX Swims Megan Ryther
Marquette Sports Law Review Volume 17 Article 8 Issue 2 Spring Swimming Upstream: Men's Olympic Swimming Sinks While Title IX Swims Megan Ryther Follow this and additional works at: http://scholarship.law.marquette.edu/sportslaw Part of the Entertainment and Sports Law Commons Repository Citation Megan Ryther, Swimming Upstream: Men's Olympic Swimming Sinks While Title IX Swims, 17 Marq. Sports L. Rev. 679 (2007) Available at: http://scholarship.law.marquette.edu/sportslaw/vol17/iss2/8 This Comment is brought to you for free and open access by the Journals at Marquette Law Scholarly Commons. For more information, please contact [email protected]. SWIMMING UPSTREAM: MEN'S OLYMPIC SWIMMING SINKS WHILE TITLE IX SWIMS* I. INTRODUCTION At the 2000 Olympic Games in Sydney, Australia, the U.S. Men's Olympic Swimming Team (the U.S. Team) was defeated for the first time ever 2 in the 4x100 Freestyle Relay' in international competition by the Australians. Many people thought this was a fluke and the United States would come back with a vengeance in 2004, but that was not the case. At the 2004 Olympic Games in Athens, Greece, the U.S. Team could not even manage to walk away with a silver medal, let alone a gold medal, in the 4x100 Freestyle Relay, an event it had once dominated. 3 The U.S. Team lost to South Africa and the 4 Netherlands, respectively, coming home with only a bronze. As one begins to search for answers as to why the United States continues to lose its dominance on the international swimming scene, an analysis of Title IX and its unintended consequences may provide some of the necessary answers. -

1999 Pan Pacific Championships Results
1999 Pan Pacific Championships Aug. 22-29, 1999 Sydney. Australia Results | 5K and 25K Open Water Results Below Top 3 and all U.S. swimmers (full results at official site) Aug. 22, 1999 Morning heats Women's 400m IM - heats *1, Maddy Crippen, USA (Philadelphia, Pa.), 4:43.13 (1:04.42, = 2:16.21, 3:36.84) 2, Joanne Malar, CAN, 4:44.76 3, Yasuko Tajima, JPN, 4:45.07 *4, Cristina Teuscher, USA (New Rochelle, N.Y.), 4:45.7 (1:05.57, = 2:18.63, 3:40.53) 13, Jenna Street, USA (Johnson City, Tenn.), 4:53.22 (1:06.35, = 2:23.50, 3:45.48) Men's 400m Free - heats 1, Grant Hackett, AUS, 3:47.37 (54.35, 1:51.76, 2:49.51) 2, Ian Thorpe, AUS, 3:48.36 3, Ryk Neethling, RSA, 3:49.47 *5, Chad Carvin, USA (Laguna Hills, Calif.), 3:52.41 (55.83, = 1:55.36, 2:55.28) *6, Jon Younghouse, USA (Cape Girardeau, Mo.), 3:52.63 (56.43, = 1:55.46, 2:54.54) 6, Chris Thompson, USA (Roseburg, Ore.), 3:52.63 (56.51, 1:54.77, = 2:53.92) 9, Erik Vendt, USA (North Easton, Mass.), 3:55.00 (55.34, 1:54.42, = 2:55.57) Women's 100m Fly - heats ^1, Jenny Thompson, USA (Dover, N.H.), 59.26 (27.95) 2, Susan O'Neill, AUS, 59.43 ^3, Misty Hyman, USA (Phoenix, Ariz.), 59.89 (27.66) ^5, Ashley Tappin, USA (New Orleans, La.), 1:00.76 (28.09) ^7, Richelle Fox, USA (Scotia, N.Y.), 1:00.85 (28.23) 13, Molly Freedman, USA (Washington, D.C.), 1:01.85 (29.41) Men's 100m Breast - heats 1, Simon Cowley, AUS, 1:01.87 (29.32) 2, Morgan Knabe, CAN, 1:02.56 ^3, Michael Norment, USA (Philadelphia, Pa.), 1:02.59 (28.93) ^11, Kurt Grote, USA (San Diego, Calif.), 1:03.54 = (29.88) Evening session -

Large-Scale Cluster Analysis of Elite Male and Female Swimmers' Race
ISSN 1750-9823 (print) International Journal of Sports Science and Engineering Vol. 02 (2008) No. 02, pp. 123-128 Large-scale Cluster Analysis of Elite Male and Female Swimmers’Race Patterns Ilene CHEN1,2 +, Ming-Yang CHEN3, Craig JIN1, Hong YAN1,4 1 School of Electrical and Information Engineering, University of Sydney, Australia 2 Swimming Australia, Australia 3 Department of Electrical Engineering, Stanford University, USA 4 Department of Electronic Engineering, City University of Hong Kong,Hong Kong (Received January10, 2008, accepted April 1, 2008) Abstract. The underlying theme of this paper is to show how large-scale cluster analysis can be applied to discover the best pacing strategy and the optimum combination of race components that will help athletes achieve their best performance at each particular race distance, which may not be observed easily otherwise. Taking into consideration the dependence of the repeated measurements made over athletes’ entire race record times over each of the i-th laps, we report three main findings: Firstly, based on the resultant tree-like dendrograms from cluster analysis, we find that male and female swimmers may use similar patterns on stroke lengths in their races whereas the swimming speeds of males are generally somewhat faster. Secondly, we demonstrate a potential application of large-scale cluster analysis to find the optimum relationship between stroke length and swimming speed that will allow German national swimmer, Stefan Herbst, and French national swimmer, Amaury Leveaux to reproduce fast swims in the 200m freestyle race distance events. Thirdly, we demonstrate a potential application of large-scale cluster analysis to find the best pacing strategy that will allow British national swimmer, Paul Palmer, Australian national swimmer, Ian Thorpe, American national swimmer, Joshua Davis, Canadian national swimmer, Rick Say, Italian national swimmers, Emiliano Brembilla and Massimiliano Rosolino, to improve their times in the 200m freestyle race distance events. -

U. S. Open Swimming Championships
USA Swimming-National Meets Hy-Tek's MEET MANAGER 5:13 PM 11/29/2002 Page 1 U. S. Open Swimming Championships - 12/5/2002 to 12/7/2002 Psych Sheet Event 1 Women 200 LC Meter IM World: 2:09.72 10/17/1997 Yanyan Wu, CHN American: 2:11.91 7/30/1992 Summer Sanders, USA U.S. Open: 2:12.64 8/3/1984 Tracy Caulkins, USA US Open Meet: 2:15.01 11/30/1990 Summer Sanders, USA Oly. Tr. Cut: 2:20.49 National Cut: 2:21.49 Name Age Team Seed Time 1 Limpert, Marianne 30 Club Aquatique 2:15.07 * 2 Cameron, Kristy 21 Univ OF Calgary Swim Club 2:16.13 3 Kowal, Kristy A 24 Athens Bulldog Swim Club-GA 2:17.88 4 Tanaka, Masami 23 Curl-Burke Swim Club-PV 2:18.79 5 Johnson, Brittany D 18 Winston-Salem Y Swim Team-NC 2:19.29 6 Axtell, Andrea L 16 Circle C Swimming-ST 2:19.37 7 Forster, Jennifer M 14 Washington Township Rec Ctr-OH 2:19.71 8 Lehner, Andrea J 14 Star Swimming-NI 2:20.02 9 Roby, Ashley E 22 Athens Bulldog Swim Club-GA 2:20.49 10 Braun, Katherine A 17 Team Foxjet-MN 2:20.88 11 Taflinger, Brooke 21 Indiana University-IN 2:20.98 12 Voyles, Lindsay A 17 Circle C Swimming-ST 2:20.99 13 Martin, Kritsy 21 Indiana University-IN 2:21.15 14 Miesner, Isabel H 18 Lakeside Swim Team-KY 2:21.44 15 Reid, Jamie L 19 University OF Florida-FL 2:21.50 16 McLarty, Sara L 19 University OF Florida-FL 2:21.52 17 Harris, Carrera A 16 Aquatic Club OF Bakersfield-CC 2:21.62 18 Hamming, Lisa C 16 Lake Forest Swim Club-IL 2:22.23 19 Mattsen, Ida 17 Sun Devil Aquatics-AZ 2:22.24 20 Lesneski, Stacie J 17 Unattached-NE 2:22.30 21 Beaudreau, Carolyn A 14 Fort Collins Area Swim Team-CO -

Victoria Amateur Swim Club
Victoria Amateur Swim Club 1990/1991 The Victoria Amateur Swim club held its annual Awards night for the 1989 / 1990 season on September 30th 1990. Vic-O’s and Cohoes are the only two clubs left from a group of island swimming clubs, formed in 1988, still competing as Island Swimming. At the Fall Nationals in Montreal November (World Trials) 11th – 17th 1990 Jon Kelly 1st – 200 Fly, Brett Regan 3rd – 400 Free, Stephan Shumka 3rd 100 Breaststroke, Nikki Dryden 1st - 100 back, 3rd - 200 back, 3rd – 400 free, Lisa Woods 3rd 200IM, medaled and represented the club The 1991 World Aquatic Championships were held in Perth Australia January 3rd to 13th, four Island Swimmers Nikki Dryden (6th – 4 X 100 Med relay), Corinne Leidtke, Jon Kelly, Greg Steppel (long distance) and a distance coach, Ron Jacks, made the team. At the 1991 Winter National in Calgary February 20th to 23rd Nikki Dryden set a new Commonwealth and Canadian record in the 200 backstroke (2:12.18), won the 100 back, and finished third in the 100 backstroke and the 400 Free. Also Jon Kelly 1st -200 Fly, Stephan Shumka 3rd – 50 Breaststroke medaled and represented the club. The 1991 Short Course TAG Club Ranking put Island Swimming 4th overall in the country. (coaches are listed as Ron Jacks et al) The 1991 Long Course TAG Club Ranking put Island Swimming 4th overall in the country. ( the coach is listed as Ron Jacks) 1 On the weekend of July 19-21 1991, two members of Island Swimming, Michael Calkins (11-12) and Suzanne Weckend (13- 14), each set three individual BC Age Group Long Course records. -

Swimming Records Long Course
SWIMMING RECORDS (Long Course) Swimming Australia Ltd. Australian - for best times recorded Date of Compilation 1 August 2021 anywhere in the World by a swimmer or team having Australian citizenship All Comers - for best times recorded Page 1 in Australia by a swimmer or team MEN 50M FREESTYLE World 20.91 Cesar Cielo BRA Sao Paulo 18.12.09 Commonwealth 21.11 Ben Proud GBR Glasgow 08.08.18 Australian 21.19 Ashley Callus North End Aq QLD Canberra 26.11.09 All Comers 21.19 Ashley Callus North End Aq QLD Canberra 26.11.09 100M FREESTYLE World 46.91 Cesar Cielo BRA Rome 30.07.09 Commonwealth 47.04 Cameron McEvoy AUS Adelaide 11.04.16 Australian 47.04 Cameron McEvoy Bond AUS Adelaide 11.04.16 All Comers 47.04 Cameron McEvoy Bond AUS Adelaide 11.04.16 200M FREESTYLE World 1:42.00 Paul Biedermann GER Rome 28.07.09 Commonwealth 1:44.06 Ian Thorpe AUS Fukuoka 25.07.01 Australian 1:44.06 Ian Thorpe SLC Aquadot NSW Fukuoka 25.07.01 All Comers 1:43.86 Michael Phelps USA Melbourne 27.03.07 400M FREESTYLE World 3:40.07 Paul Biedermann GER Rome 26.07.09 Commonwealth 3:40.08 Ian Thorpe AUS Manchester 30.07.02 Australian 3:40.08 Ian Thorpe SLC Aquadot NSW Manchester 30.07.02 All Comers 3:40.54 Ian Thorpe SLC Aquadot NSW Brisbane 18.03.02 800M FREESTYLE World 7:32.12 Lin Zhang CHN Rome 29.07.09 Commonwealth 7:38.65 Grant Hackett AUS Montreal 27.07.05 Australian 7:38.65 Grant Hackett Miami AUS Montreal 27.07.05 All Comers 7:41.59 Ian Thorpe SLC Aquadot NSW Hobart 26.03.01 1500M FREESTYLE World 14:31.02 Sun Yang CHN London 04.08.12 Commonwealth 14:34.56 Grant Hackett AUS Fukuoka 29.07.01 Australian 14:34.56 Grant Hackett Miami QLD Fukuoka 29.07.01 All Comers 14:39.54 Mack Horton Melb.