DOCSLIB.ORG

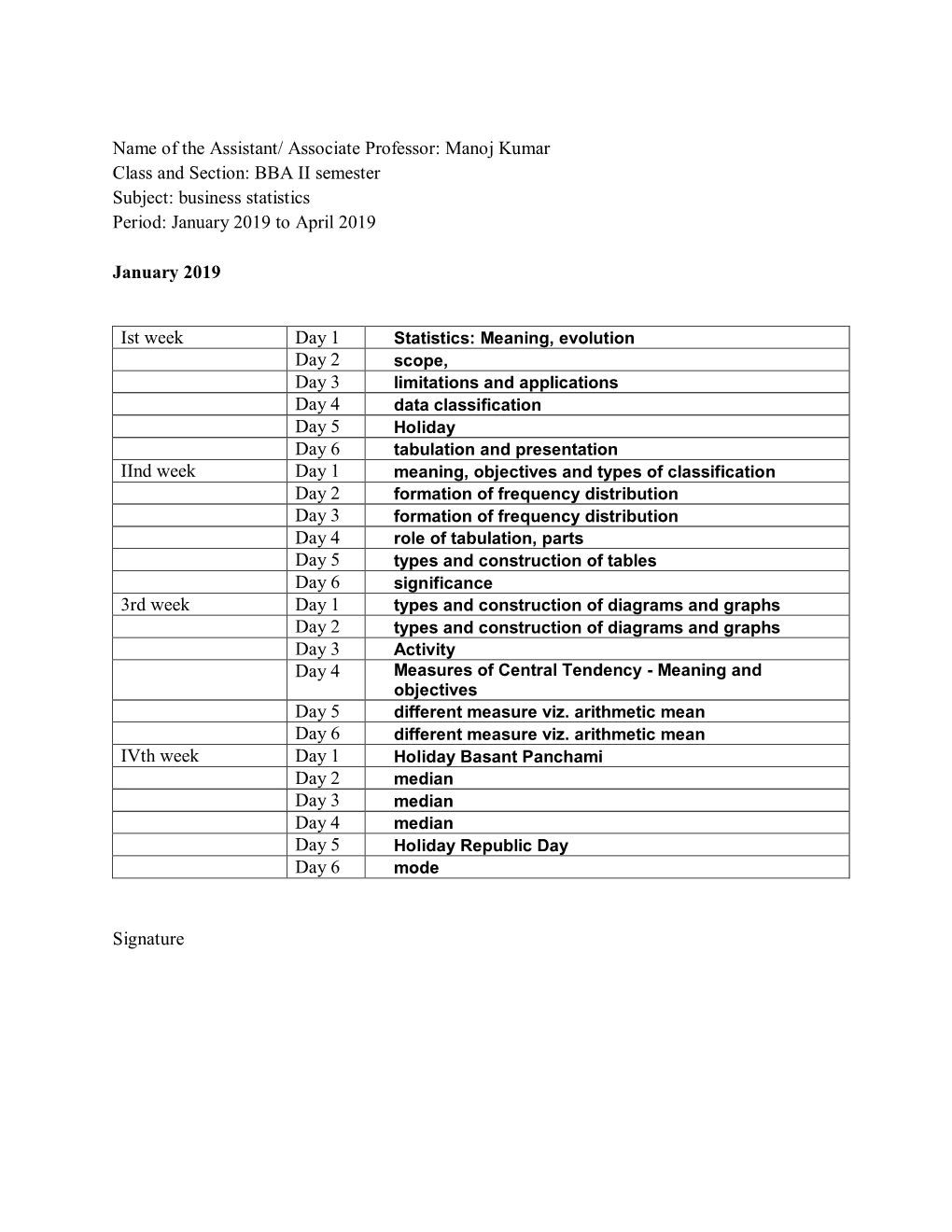
Associate Professor: Manoj Kumar Class and Section: BBA II Semester Subject: Business Statistics Period: January 2019 to April 2019

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Associate Professor: Manoj Kumar Class and Section: BBA II Semester Subject: Business Statistics Period: January 2019 to April 2019 Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: BBA II semester Subject: business statistics Period: January 2019 to April 2019 January 2019 Ist week Day 1 Statistics: Meaning, evolution Day 2 scope, Day 3 limitations and applications Day 4 data classification Day 5 Holiday Day 6 tabulation and presentation IInd week Day 1 meaning, objectives and types of classification Day 2 formation of frequency distribution Day 3 formation of frequency distribution Day 4 role of tabulation, parts Day 5 types and construction of tables Day 6 significance 3rd week Day 1 types and construction of diagrams and graphs Day 2 types and construction of diagrams and graphs Day 3 Activity Day 4 Measures of Central Tendency - Meaning and objectives Day 5 different measure viz. arithmetic mean Day 6 different measure viz. arithmetic mean IVth week Day 1 Holiday Basant Panchami Day 2 median Day 3 median Day 4 median Day 5 Holiday Republic Day Day 6 mode Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: BBA II semester Subject: business statistics Period: January 2019 to April 2019 February 2019 Ist week Day 1 geometric mean Day 2 geometric mean Day 3 harmonic mean, Day 4 harmonic mean, Day 5 characteristics, applications and limitations of these measures Day 6 numericals IInd week Day 1 numericals Day 2 measure of variation - range Day 3 Holiday Day 4 range Day 5 range Day 6 quartile deviation 3rd week Day 1 quartile deviation Day 2 mean deviation Day 3 mean deviation Day 4 mean deviation Day 5 standard deviation Day 6 standard deviation IVth week Day 1 standard deviation Day 2 standard deviation Day 3 co-efficient of variation and skewness Day 4 standard deviation Day 5 standard deviation Day 6 co-efficient of variation and skewness Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: BBA II semester Subject: business statistics Period: January 2019 to April 2019 March 2019 Ist week Day 1 co-efficient of variation and skewness Day 2 co-efficient of variation and skewness Day 3 class tests Day 4 Meaning of correlation, types of correlation Day 5 positive and negative correlation, simple, partial and multiple correlation Day 6 methods of studying correlation; scatter diagram, graphic and direct method IInd week Day 1 Regression Day 2 Regression Day 3 Regression Day 4 rank correlation, coefficient of determination Day 5 rank correlation, coefficient of determination Day 6 lines of regression, co-efficient of regression, 3rd week Day 1 lines of regression, co-efficient of regression, Day 2 lines of regression, co-efficient of regression, Day 3 standard error of estimate Day 4 standard error of estimate Day 5 standard error of estimate Day 6 Activity IVth week Day 1 Index number and their uses in business; Day 2 construction of simple and weighed price Day 3 construction of simple and weighed price Day 4 quantity and value index numbers Day 5 quantity and value index numbers Day 6 quantity and value index numbers Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: BBA II semester Subject: business statistics Period: January 2019 to April 2019 April 2019 Ist week Day 1 test for an ideal index number Day 2 components of time series viz. secular trend Day 3 components of time series viz. secular trend Day 4 cyclical, seasonal Day 5 irregular variations Day 6 methods of estimating secular trend and seasonal indices; IInd week Day 1 methods of estimating secular trend and seasonal indices; Day 2 methods of estimating secular trend and seasonal indices; Day 3 methods of estimating secular trend and seasonal indices; Day 4 Activity Day 5 use of time series in business forecasting and its limitations Day 6 Holiday 3rd week Day 1 use of time series in business forecasting and its limitations Day 2 calculating growth rate in time series Day 3 calculating growth rate in time series Day 4 calculating growth rate in time series Day 5 calculating growth rate in time series Day 6 Activity IVth week Day 1 Problem Based on coorelation Day 2 Problem Based on coorelation Day 3 problem Based on mean and median Day 4 problem based on mode Day 5 problem based on regression Day 6 problem based on standard deviation Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: B.Sc.(non medical) IV semester Subject: Special Functions And Integral Transforms Period: January 2019 to April 2019 January 2019 Ist week Day 1 Introduction of Special Function Day 2 Series solution of differential equations Day 3 Power series method Day 4 Definitions of Beta and Gamma functions Day 5 HOLIDAY Day 6 ACTIVITY IInd week Day 1 Problem based on Beta and Gamma functions Day 2 Properties based on Beta and Gamma functions Day 3 Bessel equation and its solution Day 4 Convergence, Day 5 recurrence formulae Day 6 ACTIVITY 3rd week Day 1 Relations and generating functions Day 2 Relations and generating functions Day 3 Relations and generating functions Day 4 Orthogonality of Bessel functions. Day 5 Legendre and Hermite differentials equations Day 6 ACTIVITY IVth week Day 1 HOLIDAY Day 2 Solution of Legendre and Hermite differentials equations Day 3 Solution of Legendre and Hermite differentials equations Day 4 HOLIDAY Day 5 Properties of Legendre and Hermite differentials equations Day 6 Properties of Legendre and Hermite differentials equations Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: B.Sc.(non medical) IV semester Subject: Special Functions And Integral Transforms Period: January 2019 to April 2019 February 2019 Ist week Day 1 Topic to be covered Day 2 Orhogonality of Legendre Day 3 Orhogonality of Hermite polynomial Day 4 Rodrigues’ Formula for Legendre Day 5 Rodrigues’ Formula for Hermite polynomial Day 6 Laplace Integral Representation of Legendre polynomial. IInd week Day 1 Laplace Transforms Day 2 Existence theorem for Laplace transforms Day 3 Linearity of the Laplace transforms Day 4 HOLIDAY Day 5 Shifting theorems Day 6 HOLIDAY 3rd week Day 1 Laplace transforms of derivatives Day 2 Laplace transforms of integrals Day 3 Differentiation and integration of Laplace transforms Day 4 ACTIVITY Day 5 Differentiation and integration of Laplace transforms Day 6 Convolution theorem IVth week Day 1 Problem based on Convolution theorem Day 2 Inverse Laplace transforms Day 3 Inverse Laplace transforms of derivatives and integrals Day 4 solution of ordinary differential equations using Laplace transform. Day 5 Problem based on Laplace Transform and Inverse Transform Day 6 Introduction of Fourier Transform Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: B.Sc.(non medical) IV semester Subject: Special Functions And Integral Transforms Period: January 2019 to April 2019 March 2019 Ist week Day 1 Linearity property Day 2 Shifting Theorem Day 3 , Modulation Day 4 Convolution Theorem Day 5 Problem based on convolution Day 6 ACTIVITY IInd week Day 1 Fourier Transform of Derivatives Day 2 Fourier Transform of Derivatives Day 3 Fourier Transform of Derivatives Day 4 Problem based on fourier Transform Day 5 Relations between Fourier transform and Laplace transform Day 6 ACTIVITY 3rd week Day 1 Parseval’s identity of fourier transform Day 2 Problem based on fourier Transform Day 3 Problem based on fourier cosineTransform Day 4 Problem based on fourier sine Transform Day 5 Problem based on fourier Transform Day 6 ACTIVITY IVth week Day 1 solution of differential Equations using Fourier Transforms. Day 2 solution of differential Equations using Fourier Transforms. Day 3 solution of differential Equations using Fourier Transforms. Day 4 solution of differential Equations using Fourier Transforms. Day 5 solution of differential Equations using Fourier Transforms. Day 6 ACTIVITY Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section: B.Sc.(non medical) IV semester Subject: Special Functions And Integral Transforms Period: January 2019 to April 2019 April 2019 Ist week Day 1 Problem based on special function Day 2 problem based on special function Day 3 Problem based on complete fourier transform Day 4 problem based on solution of differential equation using fourier Transform Day 5 Day 6 ACTIVITY IInd week Day 1 problem based on solution of differential equation using fourier Transform Day 2 problem based on solution of differential equation using fourier Transform Day 3 problem based on solution of differential equation using fourier Transform Day 4 problem based on solution of differential equation using fourier Transform Day 5 ACTIVITY Day 6 HOLIDAY 3rd week Day 1 problem based on solution of differential equation using fourier Transform Day 2 problem based on solution of differential equation using fourier Transform Day 3 HOLIDAY Day 4 problem based on solution of differential equation using fourier Transform Day 5 problem based on solution of differential equation using fourier Transform Day 6 ACTIVITY IVth week Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Signature Name of the Assistant/ Associate Professor: Manoj Kumar Class and Section:B.Sc.(non medical) IVsemester Subject: Sequences and Series Period: January 2019 to April 2019 January 2019 Ist week Day 1 Real Number System Day 2 Boundedness of the set of real numbers Day 3 Least upper bound, greatest lower bound of a set Day 4 Theorem based on Least Upper bound Day 5 HOLIDAY Day 6 ACTIVITY IInd week Day 1 Neighborhoods, interior points Day 2 Isolated points, limit points Day 3 Theorems based on Limit points
Load more

Recommended publications
  • Abel's Identity, 131 Abel's Test, 131–132 Abel's Theorem, 463–464 Absolute Convergence, 113–114 Implication of Condi
    INDEX Abel’s identity, 131 Bolzano-Weierstrass theorem, 66–68 Abel’s test, 131–132 for sequences, 99–100 Abel’s theorem, 463–464 boundary points, 50–52 absolute convergence, 113–114 bounded functions, 142 implication of conditional bounded sets, 42–43 convergence, 114 absolute value, 7 Cantor function, 229–230 reverse triangle inequality, 9 Cantor set, 80–81, 133–134, 383 triangle inequality, 9 Casorati-Weierstrass theorem, 498–499 algebraic properties of Rk, 11–13 Cauchy completeness, 106–107 algebraic properties of continuity, 184 Cauchy condensation test, 117–119 algebraic properties of limits, 91–92 Cauchy integral theorem algebraic properties of series, 110–111 triangle lemma, see triangle lemma algebraic properties of the derivative, Cauchy principal value, 365–366 244 Cauchy sequences, 104–105 alternating series, 115 convergence of, 105–106 alternating series test, 115–116 Cauchy’s inequalities, 437 analytic functions, 481–482 Cauchy’s integral formula, 428–433 complex analytic functions, 483 converse of, 436–437 counterexamples, 482–483 extension to higher derivatives, 437 identity principle, 486 for simple closed contours, 432–433 zeros of, see zeros of complex analytic on circles, 429–430 functions on open connected sets, 430–432 antiderivatives, 361 on star-shaped sets, 429 for f :[a, b] Rp, 370 → Cauchy’s integral theorem, 420–422 of complex functions, 408 consequence, see deformation of on star-shaped sets, 411–413 contours path-independence, 408–409, 415 Cauchy-Riemann equations Archimedean property, 5–6 motivation, 297–300
    [Show full text]
  • Cauchy's Cours D'analyse
    SOURCES AND STUDIES IN THE HISTORY OF MATHEMATICS AND PHYSICAL SCIENCES Robert E. Bradley • C. Edward Sandifer Cauchy’s Cours d’analyse An Annotated Translation Cauchy’s Cours d’analyse An Annotated Translation For other titles published in this series, go to http://www.springer.com/series/4142 Sources and Studies in the History of Mathematics and Physical Sciences Editorial Board L. Berggren J.Z. Buchwald J. Lutzen¨ Robert E. Bradley, C. Edward Sandifer Cauchy’s Cours d’analyse An Annotated Translation 123 Robert E. Bradley C. Edward Sandifer Department of Mathematics and Department of Mathematics Computer Science Western Connecticut State University Adelphi University Danbury, CT 06810 Garden City USA NY 11530 [email protected] USA [email protected] Series Editor: J.Z. Buchwald Division of the Humanities and Social Sciences California Institute of Technology Pasadena, CA 91125 USA [email protected] ISBN 978-1-4419-0548-2 e-ISBN 978-1-4419-0549-9 DOI 10.1007/978-1-4419-0549-9 Springer Dordrecht Heidelberg London New York Library of Congress Control Number: 2009932254 Mathematics Subject Classification (2000): 01A55, 01A75, 00B50, 26-03, 30-03 c Springer Science+Business Media, LLC 2009 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden.
    [Show full text]
  • SFS / M.Sc. (Mathematics with Computer Science)
    Mathematics Syllabi for Entrance Examination M.Sc. (Mathematics)/ M.Sc. (Mathematics) SFS / M.Sc. (Mathematics with Computer Science) Algebra.(5 Marks) Symmetric, Skew symmetric, Hermitian and skew Hermitian matrices. Elementary Operations on matrices. Rank of a matrices. Inverse of a matrix. Linear dependence and independence of rows and columns of matrices. Row rank and column rank of a matrix. Eigenvalues, eigenvectors and the characteristic equation of a matrix. Minimal polynomial of a matrix. Cayley Hamilton theorem and its use in finding the inverse of a matrix. Applications of matrices to a system of linear (both homogeneous and non–homogeneous) equations. Theoremson consistency of a system of linear equations. Unitary and Orthogonal Matrices, Bilinear and Quadratic forms. Relations between the roots and coefficients of general polynomial equation in one variable. Solutions of polynomial equations having conditions on roots. Common roots and multiple roots. Transformation of equations. Nature of the roots of an equation Descarte’s rule of signs. Solutions of cubic equations (Cardon’s method). Biquadratic equations and theirsolutions. Calculus.(5 Marks) Definition of the limit of a function. Basic properties of limits, Continuous functions and classification of discontinuities. Differentiability. Successive differentiation. Leibnitz theorem. Maclaurin and Taylor series expansions. Asymptotes in Cartesian coordinates, intersection of curve and its asymptotes, asymptotes in polar coordinates. Curvature, radius of curvature for Cartesian curves, parametric curves, polar curves. Newton’s method. Radius of curvature for pedal curves. Tangential polar equations. Centre of curvature. Circle of curvature. Chord of curvature, evolutes. Tests for concavity and convexity. Points of inflexion. Multiplepoints. Cusps, nodes & conjugate points. Type of cusps.
    [Show full text]
  • 1 Notes for Expansions/Series and Differential Equations in the Last
    Notes for Expansions/Series and Differential Equations In the last discussion, we considered perturbation methods for constructing solutions/roots of algebraic equations. Three types of problems were illustrated starting from the simplest: regular (straightforward) expansions, non-uniform expansions requiring modification to the process through inner and outer expansions, and singular perturbations. Before proceeding further, we first more clearly define the various types of expansions of functions of variables. 1. Convergent and Divergent Expansions/Series Consider a series, which is the sum of the terms of a sequence of numbers. Given a sequence {a1,a2,a3,a4,a5,....,an..} , the nth partial sum Sn is the sum of the first n terms of the sequence, that is, n Sn = ak . (1) k =1 A series is convergent if the sequence of its partial sums {S1,S2,S3,....,Sn..} converges. In a more formal language, a series converges if there exists a limit such that for any arbitrarily small positive number ε>0, there is a large integer N such that for all n ≥ N , ^ Sn − ≤ ε . (2) A sequence that is not convergent is said to be divergent. Examples of convergent and divergent series: • The reciprocals of powers of 2 produce a convergent series: 1 1 1 1 1 1 + + + + + + ......... = 2 . (3) 1 2 4 8 16 32 • The reciprocals of positive integers produce a divergent series: 1 1 1 1 1 1 + + + + + + ......... (4) 1 2 3 4 5 6 • Alternating the signs of the reciprocals of positive integers produces a convergent series: 1 1 1 1 1 1 − + − + − + ......... = ln 2 .
    [Show full text]
  • Real Analysis Honors Exam 1 Do the Best That You Can to Respond to The
    Real Analysis Honors Exam 1 Do the best that you can to respond to the following problems. It is not required that you respond to every problem, and, in fact, it is much better to provide complete and clearly explained responses to a subset of the given problems than to provide hurried and incomplete responses to all of them. When a complete response is not possible you are encouraged to clearly explain the partial progress that you can achieve. x2 y2 z2 4 1. Prove that the ellipsoid a2 + b2 + c2 = 1 has volume 3 πabc. You may assume that this formula is correct for the spherical case where a = b = c. 2. Newton's Method: Suppose that f : R ! R is continuously differen- tiable. Newton's method is an iterative algorithm designed to approx- imate the zeros of f. Start with a first guess x0, then for each integer n > 0 find the equation of the tangent line to the graph of f at the point (xn−1; f(xn−1))), and solve for the x intercept of that line which is named xn. Show that the sequence (xn) is guaranteed to converge under the following conditions: (a) f has a zero in the interval (a; b). (b) f is twice continuous differentiable with f 0(x) > 0 and f 00(x) > 0 on (a; b). 2 3. A function f : R ! R is Gateux differentiable at x0 if the limit f(x + hv) − f(x ) lim 0 0 ; h!0 h exists for all v 2 R2, i.e.
    [Show full text]
  • Bibliography
    Bibliography 1. E. Artin, The Gamma Function, Holt, Rinehart and Winston, New York, 1964 (translated by M. Butler from the German original, Einfubrung in Die Theorie Der Gamma Function, B. G. Teubner, 1931) 2. F. Bowman, Introduction to Elliptic Functions with Applications, Dover, New York, 1961 3. N. Bourbaki, Function D'une Variable Reel/e (Theorie Elementaire), Hermann, Editeur Des Sciences et Des Arts, Paris, 1949 4. T. J. I. Bromwich, Infinite Series (Second Edition Revised), Macmillan & Co. Limited, London, 1942 5. Burrill and Knudsen, Real Variables, Holt, Rinehart and Winston, New York, 1969 6. G. Chrystal, Textbook of Algebra, Vol. II, Dover Edition 7. Courant and John, Introduction to Calculus and Analysis, Interscience Divi­ sion, John Wiley and Sons, New York, 1965 8. Phillip Franklin, Treatise on Advanced Calculus, John Wiley and Sons, New York, 1940 9. Avmer Friedman, Advanced Calculus, Holt, Rinehart and Winston, New York, 1971 10. Watson Fulks, Advanced Calculus (Third Edition), John Wiley and Sons, New York, 1978 11. Eimar Hille, Analysis, Vol. I, Blaisdell Publishing Co., 1964 Ila. E. W. Hobson, The Theory of Functions of a Real Variable, Vol. II, Dover Edition, New York, 1957 12. Konrad Knopf, Theory and Application of Infinite Series, Blackie and Sons, London, 1951 13. Konrad Knopf, Infinite Sequences and Series, Dover Edition, 1956 14. D. Mitronovic, Analytic Inequalities, Springer-Verlag, New York 15. Poly and Azego, Aufgabe Der Analysis (2 vols.) Dover 16. John Olmsted, Advanced Calculus, Appleton, Century, Crofts, New York, 1956 16a. James Pierpont, Theory of Functions of Real Variables, Vol. II, Ginn and Company, Boston, New York, Chicago, London, 1912 17.
    [Show full text]
  • Sequences (2.2.1) Sequence. a Sequence Is a Function Whose
    Sequences (2.2.1) Sequence. A sequence is a function whose domain is N. ​ ​ ​ ​ (2.2.3) Convergence of a Sequence. A sequence (an) converges to a real number a if, for every ε > 0, ​ ​ ​ ​ ​ there exists an N ∈ N such that whenever n ≥ N, it follows that |an - a| < ε. ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ (2.2.3B) Convergence of a Sequence, Topological Characterization. A sequence (an) converges to a if, ​ ​ ​ ​ ​ given any ε-neighborhoodε V (a) of a, there exists a point in the sequence after which all of the terms ​ ​ ​ ​ ​ ε are in V (aε) ⇔ every V (a) contains all but a finite number of terms of (an). ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ (2.2.7) Uniqueness of Limits. The limit of a sequence, when it exists, must be unique. ​ ​ (2.2.9) Divergence. A sequence that does not converge is said to diverge. ​ ​ (2.3.1) Bounded. A sequence (xn) is bounded if ∃ M > 0 such that |xn| < M for all n ∈ N. ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ (2.3.2) Every convergent sequence is bounded. (2.3.3) Algebraic Limit Theorem. Let lim an = a and lim bn = b. Then, (i) lim(can) = ca for all c ∈ R; (ii) ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ lim(an + bn) = a + b; (iii) lim(anbn) = ab; (iv) lim(an/bn) = a/b provided b ≠ 0. ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​​ ​ ​ ​ ​ ​ ​ ​ (2.3.4) Order Limit Theorem. Assume lim an = a and lim bn = b. Then, (i) if an ≥ 0 for all n ∈ N, then ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ a ≥ 0; (ii) if an ≥ bn for every n ∈ N, then a ≥ b; (iii) If there exists c ∈ R for which c ≤ an for all n ∈ N, ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ then c ≤ a.
    [Show full text]
  • December 16, 2011 Math 323 — Final Exam Make Sure Your Reasoning Is
    December 16, 2011 Math 323 | Final Exam Make sure your reasoning is clear. Points are specified. 1. (20 points) Prove the Mean Value Theorem for Integrals: If f is continuous on [a; b], then R b there is a point c in [a; b] for which f(c) is the \average value" ( a f)=(b − a) of f on [a; b]. (Hint for one possible proof: Denote by m and M the extreme values of f on [a; b], and use R b them to find bounds on a f.) 2. (18 points) Give examples to show the following: (a) The intersection of infinitely many nested, nonempty, bounded, open sets U1 ⊇ U2 ⊇ U3 ⊇ ::: may be empty. (b) A continuous function on a bounded open set may be unbounded. (c) A sequence in an unbounded closed set may not have a convergent subsequence. 3. (24 points) Prove the other half of the Cauchy Condensation Test: If (an) is a decreasing se- P1 P1 k quence of positive numbers and n=1 an converges, then k=0 2 a2k also converges. (Hint: It P1 P1 k−1 is enough to show that the convergence of n=2 an implies the convergence of k=1 2 a2k . Consider the diagram below.) 4. (24 points) True (in every case) or (possibly) false? If true, give a short proof. (For example, refer to a theorem.) If false, give a counterexample. (a) On a closed interval [a; b], every continuous function is the derivative of some (differen- tiable) function. (b) On a closed interval [a; b], every derivative of a (differentiable) function is a continuous function.
    [Show full text]
  • Also Called Cauchy's Condensation Test
    TMA226 17/18 A NOTE ON THE CONDENSATION TEST The condensation test (also called Cauchy's condensation test) is one of several tests that can be used to determine if a series converges or not. It is closely related to integral test, but in many cases the condensation test requires less work than the integral test. This short note presents a self-contained proof of the condensation test. We also look at the connection to the integral test, and some examples. Preliminaries Let us recall a few important definitions before we start. In particular, we define positive, decreasing and converging series. P P1 Definition 1. Let an = n=1 an be infinite series. P • We say that an is positive if an ≥ 0 for all n. P • We say that an is decreasing if an+1 ≤ an for all n. P P Definition 2. Let an be a positive series. We say that an converges if the partial sums sn = a1 + a2 + ··· + an; n = 1; 2;::: are uniformly bounded. That is, if there is some real number M ≥ 0 so that sn ≤ M 8n: (1) P If an does not converge, then we say that it diverges. P1 P Theorem 1. Let n=1 an be a positive series. Then an converges if and only if there exists a positive real number s such that m X s = lim an: (2) m!1 n=1 P Proof. Assume an converges. Then there is some real number M such that a1 + a2 + ··· + an ≤ M | {z } = sn for all n. Then, because of the least upper bound property of the real numbers, there exists some s 2 R such that s = supfs1; s2; s3;:::g: We will now show that s is the limit of the partial sums.
    [Show full text]
  • Week 2: Calculus II Notes
    Christian Parkinson GRE Prep: Calculus II Notes 1 Week 2: Calculus II Notes We concluded the Calculus I notes with Riemann integration, Fundamental Theorem of Calculus and some helpful integration techniques. However, ofter times, you will be asked to identify whether an integral converges or diverges even when you cannot find the value. This is especially true for improper integrals: those in which the integrand had a singularity or the range goes to infinity. We begin the Calculus II notes by discussing some basic convergence results. Proposition 1 (p-test). Let p 2 R. The integral Z 1 dx p 1 x converges if p > 1 and diverges otherwise. The integral Z 1 dx p 0 x converges if p < 1 and diverges otherwise. Note that as a consequence, the integral Z 1 dx p 0 x never converges. These can all be verified by a straight-forward calculation and hint at some good intuition. The borderline case is 1=x where neither integrals converge, so as a general rule, for Z 1 f(x)dx 1 to converge, we will need f(x) ! 0 faster than 1=x as x ! 1 and if g(x) has a singularity at x = 0, then for Z 1 g(x)dx 0 to converge, we need g(x) to blow up slower than 1=x as x ! 0+. Note, these \general rules" should not be seen has hard-and-fast truths, but rather heuristics which can often make it easy to verify if an integral converges or diverges. The following two theorems give more rigorous forms of these general rules.
    [Show full text]
  • MATHEMATICAL SOURCE REFERENCES Original Source
    MATHEMATICAL SOURCE REFERENCES Original source references for common mathematical ideas J. F. Barrett ISVR, University of Southampton First version 2005 Last update July 2016 1 INTRODUCTORY REMARKS This list of references originated from a notebook in which were jotted down interesting original references. Subsequently it seemed a useful project to extend and complete the list as far as time permitted, the task being an unending one. Having reached a certain stage of completeness it is made available hoping it is found useful for those interested in mathematical origins. Generally speaking, the topics mentioned are those met in a degree course in mathematics. For each entry the list attempts to give an exact source reference with comments about priority. There are now available other historical reference sources for mathematics on the internet though with a different style of presentation*. The work has been completed in its present form while Visitor to the Institute of Sound and Vibration Research, University of Southampton. ---------------------------- CONTENTS Page Alphabetical list of topics 3 Primary sources 81 Secondary sources 97 Journal abbreviations 100 ---------------------------------------------------------------------------------------- * E.g. Earliest known uses of some of the words in mathematics http://jeff560.tripod.com/a.html 2 A AFFINE CONNEXION Defined by Weyl in his thesis and used by him in General Relativity. ------------------------ H. Weyl: Reine Infinitesimal Geometrie, Diss. Math. Ann. 78 1917 H. Weyl: Raum, Zeit, Materie, Berlin 1918 (Springer), Engl. transl. from 4th edition: Space, Time, Matter 1922 (Methuen), rpt. NY (Dover) ALGEBRA The word derives from the Arabic "al-jabr" which occurred in the title of a book of the Arabic mathematician al-Khwarizmi (fl.
    [Show full text]
  • Math 5C Discussion Problems 2
    Math 5C Discussion Problems 2 Path Independence 1. Let C be the striaght-line path in R2 from the origin to (3; 1). Define f(x; y) = xyexy. Z (a) Evaluate rf · dr. C Z (b) Evaluate ((1; 0) + rf) · dr. C Z (c) Evaluate ((y; 0) + rf) · dr. C 2. Let C be the positively oriented unit circle in R2 centered at the origin. I (a) Evaluate y dx − x dy. C (b) Use the previous part to explain why (y; −x) isn't the gradient of a function. 3. For each of the following vector fields, determine whether it is the gradient of a function. (a) (4x2 − 4y2 + x; 7xy + ln y) on R2 (b) (3x2 ln x + x2; x3=y) on R2 (c) (x3y; 0; z2) on R3 4. For each of the following, find the function f. (a) f(0; 0; 0) = 0 and rf = (x; y; z) (b) f(1; 2; 3) = 4 and rf = (5; 6; 7) (c) f(1; 1; 1) = 1 and rf = (2xyz + sin x; x2z; x2y) 5. For which a is (ax ln y; 2y + x2=y) the gradient of a function in (some subset of) R2? Z 3 6. Let C be a curve in R2 given by r(t) = (cos5 t; sin t; t4), where 0 ≤ t ≤ π. Evaluate (yz; xz; xy) · dr. C Green's Theorem 1. Let D be the unit disk centered at the origin in R2. I (a) Evaluate dx + x dy. @D I (b) Evaluate arctan(esin x) dx + y dy. @D I (c) Evaluate (x3 − y3) dx + (x3 + y3) dy.
    [Show full text]