DOCSLIB.ORG

01 Front Matter

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

CANADIAN MATHEMATICS EDUCATION STUDY GROUP GROUPE CANADIEN D’ÉTUDE EN DIDACTIQUE DES MATHÉMATIQUES PROCEEDINGS / ACTES 2004 ANNUAL MEETING Université Laval May 28 – June 1, 2004 EDITED BY: Elaine Simmt, University of Alberta Brent Davis, University of Alberta CANADIAN MATHEMATICS EDUCATION STUDY GROUP GROUPE CANADIEN D’ÉTUDE EN DIDACTIQUE DES MATHÉMATIQUES PROCEEDINGS / ACTES 2004 ANNUAL MEETING Université Laval May 28 – June 1, 2004 EDITED BY: Elaine Simmt, University of Alberta Brent Davis, University of Alberta Proceedings of the 2004 Annual Meeting of the Canadian Mathematics Education Study Group / Groupe Canadien d’Étude en Didactique des Mathématiques are published by CMESG/GCEDM. They were printed in April 2005 in Edmonton, AB. Proceedings of the 2004 Annual Meeting of the Canadian Mathematics Education Study Group / Groupe Canadien d’Étude en Didactique des Mathématiques 28th Annual Meeting Université Laval May 28 – June 1, 2004 Contents / Table des matières v Remerciements vii Schedule FRÉDÉRIC GOURDEAU ix Introduction Plenary Lectures / Conférences plénières CLAIRE MARGOLINAS 3 La situation du professeur et les connaissances en jeu au cours de l’activité mathématique en classe NICOLAS BOULEAU 23 La personnalité d’Evariste Galois : le contexte psychologique d’un goût prononcé pour les mathématiques abstraites Working Groups / Groupes de travail NATHALIE SINCLAIR, ANNE 45 A • Learner-Generated Examples WATSON, & RINA ZAZKIS TOM O’SHEA & PETER TAYLOR 55 B • Transition to University Mathematics FRANCE CARON & 63 C • L’intégration de l’application et de la modélisation dans les mathé- ERIC MULLER matiques au secondaire et au collégial / Integrating Applications and Modelling in Secondary and Postsecondary Mathematics ANN KAJANDER & 81 D • Elementary Teacher Education: Defining the Crucial JEAN DIONNE Experiences GEOFF ROULET & 87 E • La technologie dans l’enseignement des mathématiques : ANDRÉ BOILEAU regard critique sur le discours et la pratique / A Critical Look at the Language and Practice of Mathematics Education Topic Sessions / Sessions thématiques RENÉE CARON 99 L’enseignement des probabilités dans les écoles primaires du Québec DAVE HEWITT 105 Feedback LUIS RADFORD 111 Body, Tool, and Symbol: Semiotic Reflections on Cognition STEVE THORNTON 119 Standards for Excellence in Teaching Mathematics iii New PhD Reports / Présentations de thèses de doctorat PETER LILJEDAHL 129 The AHA! Experience: Mathematical Contexts, Pedagogical Implications LAURENT THEIS 135 The Issues of Learning the Equals Sign for Grade 1 Students Ad Hoc Sessions / Séances ad hoc A. J. (SANDY) DAWSON 145 Measuring the Impact of a Mentor Program DOUGLAS MCDOUGALL 147 Ten Dimensions of Mathematics Education—A Framework for Improving Mathematics TOM STEINKE & 149 To JUMP or not to JUMP STEWART CRAVEN KALIFA TRAORÉ, CAROLINE 151 Undergraduate Students’ Errors That May Be Related to LAJOIE, & ROBERTA MURA Confusing a Set with Its Elements DAVID WAGNER 153 Expressing Mathematical Fluency Panel Discussion / Table Rond DAVID A. REID 157 What is Canadian about Canadian Mathematics Education? / La didactique des mathématiques au Canada se distingue-t-elle de ce qui se fait ailleurs dans le monde ? ERIC MULLER 165 What are the Issues and Problems Facing Mathematical Education in Canada? THOMAS E. KIEREN 169 Unique Features of the Body of Mathematics Education in Canada: A Brief Sketch Appendices 173 A • Working Groups at Each Annual Meeting 177 B • Plenary Lectures at Each Annual Meeting 181 C • Proceedings of Annual Meetings 183 D • List of Participants iv Remerciements Le travail d’organisation de la rencontre annuelle de 2004 à l’Université Laval a été couronné d’un grand succès. Caroline Lajoie, coordonnatrice des rencontres annuelles au sein de l’exécutif du groupe, y est pour beaucoup. Sur le plan local, nous remercions Bernard R. Hodgson et Frédéric Gourdeau, qui ont su organiser la rencontre annuelle avec efficacité et entrain, Sylvie Drolet, qui a fourni un appui technique impeccable, ainsi que Jean-Lou De Carufel, Jean-François Maheux et Luc Tremblay, les trois étudiants qui ont aidé à ce que tout se déroule sans mauvaise surprise. Les éditeurs voudraient remercier (en français !) Jérôme Proulx pour l’aide fournie à la vérification des documents écrits en français. v Schedule Vendredi/ Samedi/ Dimanche/ Lundi/ Mardi/ Friday Saturday Sunday Monday Tuesday May 28 mai May 29 mai May 30 mai May 31 mai June 01 juin 1234567890123 1234567890123 1234567890123 9h00–9h30 1234567890123 1234567890123 New PhDs/Thèses 1234567890123 1234567890123 1234567890123 1234567890123 9h30–11h00 1234567890123 1234567890123 Table ronde/Panel 1234567890123 1234567890123 09h00–12h15 Matin/ 1234567890123 Groupes de travail / Working Groups Morning1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 1234567890123 11h30–12h30 1234567890123 1234567890123 Séance de cloture/ 1234567890123 1234567890123 Closing Session 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12h15–13h45 12345678901234 1234567890123 12345678901234 1234567890123 Dîner / Lunch 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 13h45–14h30 13h45–14h45 13h45–14h30 12345678901234 1234567890123 12345678901234 1234567890123 Petits groupes/ Conférence 2/ Petits groupes/ 12345678901234 1234567890123 12345678901234 1234567890123 Small Groups Plenary 2: Small Groups 12345678901234 Bouleau 12345678901234 14h30–15h30 14h30–15h30 12345678901234 12345678901234 Discussion de/of 14h45–15h15 Discussion de/of 12345678901234 Après- 12345678901234 Ad Hocs midi/ 14h30–16h30 Margolinas 12345678901234 Bouleau 12345678901234 1234567890123451234567890123412345678901234512345678901234 After- Registration/ 1234567890123415234567890123142345678901234152345678901234 1234567890123415234567890123142345678901234152345678901234 noon Inscription 1234567890123451234567890123412345678901234512345678901234 12345678901234 16h00–16h30 12345678901234 12345678901234 1234567890123 Ad Hocs 12345678901234 1234567890123 12345678901234 16h00–18h00 12345678901234 12345678901234 16h45–17h45 Groupes thématiques/ 16h30–18h00 12345678901234 12345678901234 Cocktails Topic Groups AGA / AGM 12345678901234 GDM/CMESG 12345678901234 12345678901234 15h30– 12345678901234 Excursion 12345678901234 17h45–18h45 18h00–18h30 12345678901234 12345678901234 Souper/Supper New PhDs/Thèses 18h00– 12345678901234 12345678901234 Excursion 12345678901234 18h45–19h30 12345678901234 to/au 12345678901234 Opening 18h30–20h00 Manoir 12345678901234 12345678901234 Soir/ BBQ Montmorency 12345678901234 19h30–20h30 12345678901234 Evening 12345678901234 Conférence 1/ 12345678901234 12345678901234567890123456789012123456789012345678901234 Plenary 1: 12345678901234567890123456789012123456789102345678901234 Margolinas 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 20h30 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 Reception 12345678901234567890123456789012123456789012345678901234 vii Introduction Frédéric Gourdeau - Président, CMESG/GCEDM Université Laval La rencontre annuelle 2004 du GCEDM/CMESG a permis de poursuivre la tradition d’excellence établie au fil des ans. La richesse des échanges et le plaisir manifeste que nous avons eus à travailler ensemble ont fait de cette rencontre une grande réussite. Le contenu des Actes vous permettra d’en apprécier la valeur. La rencontre 2004 avait une saveur particulière : tenue dans la ville de Québec, la présence francophone y était plus marquée qu’à l’habitude. Ainsi, avant même le début de la rencontre annuelle, les membres étaient conviés à des échanges avec le GDM (Groupe de Didactique des Mathématiques du Québec). En effet, l’exécutif avait réussi à organiser la rencontre annuelle en collaboration avec le GDM, ce qui a permis une plus grande partici- pation des membres du GDM aux activités de GCEDM. La conférence de Jacques Bélair, donnée dans le cadre de la rencontre du GDM, ainsi que le conférence d’ouverture de la rencontre annuelle du GCEDM, donnée par Claire Margolinas, étaient ouvertes aux membres des deux groupes. Les échanges fructueux qui ont suivi, agrémentés d’un cocktail offert conjointement par la Faculté des Sciences de l’éducation et par la Faculté des sciences et de génie de l’Université Laval, sont un témoignage de l’intérêt d’une telle initiative. France Caron, pour le GDM, et Caroline Lajoie, pour le GCEDM, sont les principales responsables de cette belle réussite, et nous les en remercions. Of course, the cultural impact of a meeting in Québec was not only visible in the larger participation by francophones at our meeting: it also manifested itself in the importance given to the evening meals which occupied us for many hours each day, and to the singing which accompanied two of those meals. Thanks to everyone for so playfully taking part in those activities. En ce qui a trait au contenu des échanges que nous avons eus, je ne peux tous les commenter. Je peux certainement souligner les contributions de nos deux brillants conférenciers pléniers, Claire Margolinas et Nicolas Bouleau, ainsi que les réflexions de Claude Gaulin, Tom Kieren, Eric Muller et David Reid lors du panel du mardi matin. En ce qui a trait aux
Recommended publications
  • La Voix Humaine: a Technology Time Warp

    La Voix Humaine: a Technology Time Warp

    University of Kentucky UKnowledge Theses and Dissertations--Music Music 2016 La Voix humaine: A Technology Time Warp Whitney Myers University of Kentucky, [email protected] Digital Object Identifier: http://dx.doi.org/10.13023/ETD.2016.332 Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Myers, Whitney, "La Voix humaine: A Technology Time Warp" (2016). Theses and Dissertations--Music. 70. https://uknowledge.uky.edu/music_etds/70 This Doctoral Dissertation is brought to you for free and open access by the Music at UKnowledge. It has been accepted for inclusion in Theses and Dissertations--Music by an authorized administrator of UKnowledge. For more information, please contact [email protected]. STUDENT AGREEMENT: I represent that my thesis or dissertation and abstract are my original work. Proper attribution has been given to all outside sources. I understand that I am solely responsible for obtaining any needed copyright permissions. I have obtained needed written permission statement(s) from the owner(s) of each third-party copyrighted matter to be included in my work, allowing electronic distribution (if such use is not permitted by the fair use doctrine) which will be submitted to UKnowledge as Additional File. I hereby grant to The University of Kentucky and its agents the irrevocable, non-exclusive, and royalty-free license to archive and make accessible my work in whole or in part in all forms of media, now or hereafter known. I agree that the document mentioned above may be made available immediately for worldwide access unless an embargo applies.
  • Semantic Skin: from Flat Textual Content to Interconnected Repositories Of

    Semantic Skin: from Flat Textual Content to Interconnected Repositories Of

    Semantic Skin: from flat textual content to interconnected repositories of semantic data. Claudio Baldassarre ABSTRACT front-end web application. This application offers a faceted One approach to re-balancing the Digital Divide tends to view of the underlying \news-KB". The current blog site favor the production of informative content in flat formats, appearance is merely a stylistic choice, while a running in- which are easy to distribute and consume. At the same time stance is always backed by a SPARQL endpoint over the this approach forbids to deliver the core knowledge perti- \news-KB". The facets are typically rendered as menu ele- nent within the content; i.e. it increases the Knowledge ments5: some menus facet the entire \news-KB" (e.g., news Divide. In some international organizations1, informative Topics, or Provenance); while other menus facet only the content distribution to groups in Latin America happens by content currently visible to the users. The faceting mech- manually collecting text-based content, then disseminating anism is also applied tothe \news archive" as a time-based it via standard mailing lists, or databases copies sent out facet of the repository content. All the facets are popu- regularly. Our demo showcases the use of Semantic Skin lated with SPARQL queries over the \news-model" instances a technology that after semantifying the content submit- in the \news-KB". Each news item is then presented with ted in flat formats, provides access to the information via a its summary, title, publication date, and provenance (e.g., knowledge layer, which is, however, transparent to the end permalink).
  • Where Is the Semantic Web? – an Overview of the Use of Embeddable Semantics in Austria

    Where Is the Semantic Web? – an Overview of the Use of Embeddable Semantics in Austria

    Where Is The Semantic Web? – An Overview of the Use of Embeddable Semantics in Austria Wilhelm Loibl Institute for Service Marketing and Tourism Vienna University of Economics and Business, Austria [email protected] Abstract Improving the results of search engines and enabling new online applications are two of the main aims of the Semantic Web. For a machine to be able to read and interpret semantic information, this content has to be offered online first. With several technologies available the question arises which one to use. Those who want to build the software necessary to interpret the offered data have to know what information is available and in which format. In order to answer these questions, the author analysed the business websites of different Austrian industry sectors as to what semantic information is embedded. Preliminary results show that, although overall usage numbers are still small, certain differences between individual sectors exist. Keywords: semantic web, RDFa, microformats, Austria, industry sectors 1 Introduction As tourism is a very information-intense industry (Werthner & Klein, 1999), especially novel users resort to well-known generic search engines like Google to find travel related information (Mitsche, 2005). Often, these machines do not provide satisfactory search results as their algorithms match a user’s query against the (weighted) terms found in online documents (Berry and Browne, 1999). One solution to this problem lies in “Semantic Searches” (Maedche & Staab, 2002). In order for them to work, web resources must first be annotated with additional metadata describing the content (Davies, Studer & Warren., 2006). Therefore, anyone who wants to provide data online must decide on which technology to use.
  • Appendix a the Ten Commandments for Websites

    Appendix a the Ten Commandments for Websites

    Appendix A The Ten Commandments for Websites Welcome to the appendixes! At this stage in your learning, you should have all the basic skills you require to build a high-quality website with insightful consideration given to aspects such as accessibility, search engine optimization, usability, and all the other concepts that web designers and developers think about on a daily basis. Hopefully with all the different elements covered in this book, you now have a solid understanding as to what goes into building a website (much more than code!). The main thing you should take from this book is that you don’t need to be an expert at everything but ensuring that you take the time to notice what’s out there and deciding what will best help your site are among the most important elements of the process. As you leave this book and go on to updating your website over time and perhaps learning new skills, always remember to be brave, take risks (through trial and error), and never feel that things are getting too hard. If you choose to learn skills that were only briefly mentioned in this book, like scripting, or to get involved in using content management systems and web software, go at a pace that you feel comfortable with. With that in mind, let’s go over the 10 most important messages I would personally recommend. After that, I’ll give you some useful resources like important websites for people learning to create for the Internet and handy software. Advice is something many professional designers and developers give out in spades after learning some harsh lessons from what their own bitter experiences.
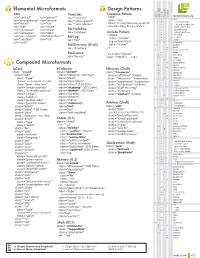
  • Microformats Cheat Sheet

    Microformats Cheat Sheet

    Elemental Microformats Design Patterns tom eview Datetime Pattern esume XFN VoteLinks microformats.org hR hR hCard hCalendar rel="contact" rel="parent" rev="vote-for" <abbr hA rel="acquaintance" rel="spouse" class="foo" • adr rev="vote-against" + country-name title="YYYY-MM-DDTHH:MM:SS+ZZ:ZZ" rel="friend" rel="kin" rev="vote-abstain" • extended-address rel="met" rel="muse" >Human Date Time</abbr> + post-office-box rel="co-worker" rel="crush" Rel-Nofollow + postal-code rel="colleague" rel="date" rel="nofollow" Include Pattern • street-address + locality rel="co-resident" rel="sweetheart" <object Rel-Tag class="include" + region rel="neighbor" rel="me" rel="tag" • type rel="child" type="text/html" • affiliation Rel-Directory (Draft) data="#idref" ¤ author rel="directory" /> + best × + bookmark (rel) Rel-License + bday <a class="include" • • category rel="license" href="#idref">...</a> + + class × contact Compound Microformats + description + dtend + dtreviewed hCard hCalendar hResume (Draft) × dtstart class="vcard" class="vevent" class="hresume" × dtstamp class="adr" class="category" rel="tag" class="affiliation" (hcard) duration class="type" class="class" class="education" (hcalendar) • education [work|home|pref|postal|dom|intl] class="description" • email class="experience" (hcalendar) • type class="post-office-box" class="dtend" (ISO Date) class="publication" (citation) • value class="street-address" class="dtstamp" (ISO Date) class="skill" rel="tag" × entry-content class="extended-address" class="dtstart" (ISO Date) class="summary" • entry-summary
  • Y A-T-Il Encore De La Place En Bas ? Le Paysage Contemporain Des Nanosciences Et Des Nanotechnologies

    Y A-T-Il Encore De La Place En Bas ? Le Paysage Contemporain Des Nanosciences Et Des Nanotechnologies

    Philosophia Scientiæ Travaux d'histoire et de philosophie des sciences 23-1 | 2019 Y a-t-il encore de la place en bas ? Le paysage contemporain des nanosciences et des nanotechnologies Jonathan Simon et Bernadette Bensaude-Vincent (dir.) Édition électronique URL : http://journals.openedition.org/philosophiascientiae/1693 DOI : 10.4000/philosophiascientiae.1693 ISSN : 1775-4283 Éditeur Éditions Kimé Édition imprimée Date de publication : 18 février 2019 ISSN : 1281-2463 Référence électronique Jonathan Simon et Bernadette Bensaude-Vincent (dir.), Philosophia Scientiæ, 23-1 | 2019, « Y a-t-il encore de la place en bas ? » [En ligne], mis en ligne le 01 janvier 2021, consulté le 30 mars 2021. URL : http://journals.openedition.org/philosophiascientiae/1693 ; DOI : https://doi.org/10.4000/ philosophiascientiae.1693 Tous droits réservés Y a-t-il encore de la place en bas ? Le paysage contemporain des nanosciences et des nanotechnologies Introduction. Nanotechnoscience: The End of the Beginning Bernadette Bensaude-Vincent Université Paris 1 Panthéon-Sorbonne (France) Jonathan Simon Archives Henri-Poincaré – Philosophie et Recherches sur les Sciences et les Technologies (AHP-PReST), Université de Lorraine, Université de Strasbourg, CNRS, Nancy (France) Is there still room at the bottom? The question providing the theme for the present issue of Philosophia Scientiæ is, of course, adapted from Richard Feynman’s well-known speech at the 1959 meeting of the American Physical Society. On this occasion he attracted physicists’ attention to the vast potential of working at the scale of the nanometre if not the ångström, using the catchy title: “Plenty of Room at the Bottom” [Feynman 1959]. This hookline from a famous Nobel laureate physicist served as a motto for the emerging field of nanoscience and nanotechnology (which we will here abbreviate to nanoresearch) in the early 2000s.
  • Microformats: Empowering Your Markup for Web 2.0

    Microformats: Empowering Your Markup for Web 2.0

    Microformats: Empowering Your Markup for Web 2.0 John Allsopp Microformats: Empowering Your Markup for Web 2.0 Copyright © 2007 by John Allsopp All rights reserved. No part of this work may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage or retrieval system, without the prior written permission of the copyright owner and the publisher. ISBN-13 (pbk): 978-1-59059814-6 ISBN-10 (pbk): 1-59059-814-8 Printed and bound in the United States of America 9 8 7 6 5 4 3 2 1 Trademarked names may appear in this book. Rather than use a trademark symbol with every occurrence of a trademarked name, we use the names only in an editorial fashion and to the benefit of the trademark owner, with no intention of infringement of the trademark. Distributed to the book trade worldwide by Springer-Verlag New York, Inc., 233 Spring Street, 6th Floor, New York, NY 10013. Phone 1-800-SPRINGER, fax 201-348-4505, e-mail [email protected],or visit www.springeronline.com. For information on translations, please contact Apress directly at 2560 Ninth Street, Suite 219, Berkeley, CA 94710. Phone 510-549-5930, fax 510-549-5939, e-mail [email protected], or visit www.apress.com. The information in this book is distributed on an “as is” basis, without warranty. Although every precaution has been taken in the preparation of this work, neither the author(s) nor Apress shall have any liability to any person or entity with respect to any loss or damage caused or alleged to be caused directly or indirectly by the information contained in this work.
  • Standardization's All Very Well, but What About the Exabytes of Existing

    Standardization's All Very Well, but What About the Exabytes of Existing

    Standardization’s all very well, but what about the Exabytes of Existing Content and Learner Contributions? Felix Mödritscher 1), Victor Manuel García-Barrios 2) 1) Institute for Information Systems and New Media, Vienna University of Economics and Business Administration, Augasse 2-6, 1090 Vienna, Austria [email protected] 2) Institute for Information Systems and Computer Media, Graz University of Technology, Inffeldgasse 16c, 8010 Graz, Austria [email protected] 1. Problem Definition Standardization in the field of technology-enhanced learning focuses on structuring and aggregating assets to interoperable educational entities, like a course package. However, available standards and specifications in this area do not include an approach for addressing semantics embedded in existing content. This consideration might be useful for user-centered concepts, like learners tagging or commenting existing material, as well as for automated mechanism, like extracting relations or other meta-information automatically from the resources. In the upcoming section we indicate application areas and explain why available standards and specifications do not support these scenarios. Thereafter, we present a XML- based description language for semantics embedded in web-based content, which might be a solution for these use cases. Finally, we summarize and discuss some experiences on in- content semantics from former projects, particularly AdeLE (Adaptive e-Learning with Eye- tracking, http://adele.fh-joanneum.at) and iCamp (http://icamp.eu), and give an outlook on future work. 2. Application Areas and Shortcomings of Standards In 2004 we came in the situation that we had to cope with semantic enrichment of existing learning content, precisely to enable facilitators to tag web-based resources.
  • The Global Rock-Art Database

    The Global Rock-Art Database

    The Global Rock-Art Database: Centralizing Heritage Data Collections using a Collaborative, Information Structure and Data Visualization Approach in an Open Source Application Author Haubt, Robert Alexander Published 2016 Thesis Type Thesis (PhD Doctorate) School School of Humanities, Languages and Social Science DOI https://doi.org/10.25904/1912/3082 Copyright Statement The author owns the copyright in this thesis, unless stated otherwise. Downloaded from http://hdl.handle.net/10072/367148 Griffith Research Online https://research-repository.griffith.edu.au The Global Rock-Art Database Centralizing Heritage Data Collections using a Collaborative, Information Structure and Data Visualization Approach in an Open Source Application Mr. Robert Alexander Haubt BA (Hons), MA School of Humanities, Languages and Social Sciences Griffith University Submitted in fulfillment of the requirements of the degree of Doctor of Philosophy May 2016 Statement of Originality This work has not previously been submitted for a degree or diploma in any university. To the best of my knowledge and belief, the thesis contains no material previously published or written by another person except where due reference is made in the thesis itself. _____________________________ Robert A. Haubt I Acknowledgments Acknowledgments Firstly, I would like to express my sincere gratitude to my supervisor Prof. P.S.C. Taçon for the support of my PhD research during the last four years. His patience, motivation and knowledge helped guide me through my research and I could not have imagined a better mentor for my PhD studies. Besides my supervisor, I would like to thank Dr. Duncan Wright, Dr. Tim Humphrey and Dr. Jason Nelson for their guidance and support as my associate supervisors.
  • Arxiv:2010.04222V1 [Cond-Mat.Mtrl-Sci] 8 Oct 2020

    Arxiv:2010.04222V1 [Cond-Mat.Mtrl-Sci] 8 Oct 2020

    AFLOW-XtalFinder: a reliable choice to identify crystalline prototypes David Hicks,1, 2 Cormac Toher,1, 2 Denise C. Ford,1, 2 Frisco Rose,1, 2 Carlo De Santo,1, 2 Ohad Levy,1, 2, 3 Michael J. Mehl,1, 2 and Stefano Curtarolo1, 2, ∗ 1Department of Mechanical Engineering and Materials Science, Duke University, Durham, North Carolina 27708, USA 2Center for Autonomous Materials Design, Duke University, Durham, North Carolina 27708, USA 3Department of Physics, NRCN, P.O. Box 9001, Beer-Sheva 84190, Israel (Dated: October 12, 2020) The accelerated growth rate of repository entries in crystallographic databases makes it arduous to identify and classify their prototype structures. The open-source AFLOW-XtalFinder package was developed to solve this problem. It symbolically maps structures into standard designations following the AFLOW Prototype Encyclopedia and calculates the internal degrees of freedom consistent with the International Tables for Crystallography. To ensure uniqueness, structures are analyzed and compared via symmetry, local atomic geometries, and crystal mapping techniques, simultaneously grouping them by similarity. The software i. distinguishes distinct crystal prototypes and atom decorations, ii. determines equivalent spin configurations, iii. reveals compounds with similar properties, and iv. guides the discovery of unexplored materials. The operations are accessible through a Python module ready for workflows, and through command line syntax. All the 4+ million compounds in the AFLOW.org repositories are mapped to their ideal prototype, allowing users to search database entries via symbolic structure-type. Furthermore, 15,000 unique structures | sorted by prevalence | are extracted from the AFLOW-ICSD catalog to serve as future prototypes in the Encyclopedia.
  • Miranda, 15 | 2017, « Lolita at 60 / Staging American Bodies » [En Ligne], Mis En Ligne Le 18 Septembre 2017, Consulté Le 16 Février 2021

    Miranda, 15 | 2017, « Lolita at 60 / Staging American Bodies » [En Ligne], Mis En Ligne Le 18 Septembre 2017, Consulté Le 16 Février 2021

    Miranda Revue pluridisciplinaire du monde anglophone / Multidisciplinary peer-reviewed journal on the English- speaking world 15 | 2017 Lolita at 60 / Staging American Bodies Édition électronique URL : http://journals.openedition.org/miranda/10470 DOI : 10.4000/miranda.10470 ISSN : 2108-6559 Éditeur Université Toulouse - Jean Jaurès Référence électronique Miranda, 15 | 2017, « Lolita at 60 / Staging American Bodies » [En ligne], mis en ligne le 18 septembre 2017, consulté le 16 février 2021. URL : http://journals.openedition.org/miranda/10470 ; DOI : https:// doi.org/10.4000/miranda.10470 Ce document a été généré automatiquement le 16 février 2021. Miranda is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. 1 SOMMAIRE Les 60 ans de Lolita Introduction Marie Bouchet, Yannicke Chupin, Agnès Edel-Roy et Julie Loison-Charles Nabokov et la censure Julie Loison-Charles Lolita, le livre « impossible » ? L'histoire de sa publication française (1956-1959) dans les archives Gallimard Agnès Edel-Roy Fallait-il annoter Lolita? Suzanne Fraysse The patterning of obsessive love in Lolita and Possessed Wilson Orozco Publicités, magazines, et autres textes non littéraires dans Lolita : pour une autre poétique intertextuelle Marie Bouchet Solipsizing Martine in Le Roi des Aulnes by Michel Tournier: thematic, stylistic and intertextual similarities with Nabokov's Lolita Marjolein Corjanus Les « Variations Dolores » - 2010-2016 Nouvelles lectures-réécritures de Lolita Yannicke Chupin Staging American Bodies Staging American Bodies – Introduction Nathalie Massip Spectacle Lynching and Textual Responses Wendy Harding Bodies of War and Memory: Embodying, Framing and Staging the Korean War in the United States Thibaud Danel Singing and Painting the Body: Walt Whitman and Thomas Eakins’ Approach to Corporeality Hélène Gaillard “It’s so queer—in the next room”: Docile/ Deviant Bodies and Spatiality in Lillian Hellman’s The Children’s Hour Sarah A.
  • UNIVERSITE D'aix-MARSEILLE Human RNA Bait Library Depletion for Human (Viral) Pathogen Discovery Using Shotgun Metagenomic Se

    UNIVERSITE D'aix-MARSEILLE Human RNA Bait Library Depletion for Human (Viral) Pathogen Discovery Using Shotgun Metagenomic Se

    UNIVERSITE D’AIX-MARSEILLE ECOLE DOCTORALE DES SCIENCES DE LA VIE ET DE LA SANTE Unité de recherche : Microbes, Evolution, Phylogeny and Infection (MEPHI) Thèse présentée pour obtenir le grade de DOCTEUR d’AIX-MARSEILLE UNIVERSITE Discipline : Pathologie Humaine / Spécialité : Maladies Infectieuses Par Mr GAUDIN Maxime Human RNA bait library depletion for human (viral) pathogen discovery using shotgun metagenomic sequencing Soutenue le 23 novembre 2018 Membres du jury de la thèse : Mr le Professeur Philippe COLSON Président du jury Mr le Professeur Bruno POZZETTO Rapporteur Mr le Docteur Philippe ROUMAGNAC Rapporteur Mme le Docteur Christelle DESNUES Directrice de thèse IHU Méditerranée Infection, 19-21 Boulevard Jean Moulin, 13005 Marseille Résumé Le développement des techniques de séquençage de nouvelle génération (NGS) a révolutionné la recherche et le diagnostic dans le domaine des maladies infectieuses humaines. En virologie clinique, la métagénomique virale qui repose sur le séquençage aléatoire de type shotgun de l’ensemble des génomes viraux d’un échantillon (le virome), est une approche prometteuse pour la détection et l’identification sans a priori de potentiels nouveaux pathogènes. Cependant, son utilisation reste encore marginale en raison de l’importante contamination des viromes par les séquences nucléiques de l’hôte qui masque le signal viral, limite la reconstruction de génomes viraux et requiert une profondeur importante de séquençage, générant ainsi un cout élevé. Ces dernières années, de nombreux protocoles reposant principalement sur des étapes de filtration/centrifugation et digestions enzymatiques, ont été développés pour diminuer cette contamination humaine avec un succès limité notamment dans le cas de biopsies cliniques. Dans ce contexte, ce travail de thèse avait pour objectif d’améliorer l’approche de métagénomique pour le diagnostic clinique de maladies infectieuses virales en augmentant le ratio de séquences pathogène/hôte par déplétion des acides nucléiques humains.