DOCSLIB.ORG

Photometric Phase Variations of Long-Period Eccentric Planets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Photometric Phase Variations of Long-Period Eccentric Planets Submitted for publication in the Astrophysical Journal A Preprint typeset using LTEX style emulateapj v. 03/07/07 PHOTOMETRIC PHASE VARIATIONS OF LONG-PERIOD ECCENTRIC PLANETS Stephen R. Kane, Dawn M. Gelino NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue, Pasadena, CA 91125, USA Submitted for publication in the Astrophysical Journal ABSTRACT The field of exoplanetary science has diversified rapidly over recent years as the field has progressed from exoplanet detection to exoplanet characterization. For those planets known to transit, the pri- mary transit and secondary eclipse observations have a high yield of information regarding planetary structure and atmospheres. The current restriction of these information sources to short-period plan- ets may be abated in part through refinement of orbital parameters. This allows precision targeting of transit windows and phase variations which constrain the dynamics of the orbit and the geomet- ric albedo of the atmosphere. Here we describe the expected phase function variations at optical wavelengths for long-period planets, particularly those in the high-eccentricity regime and multiple systems in resonant and non-coplanar orbits. We apply this to the known exoplanets and discuss detection prospects and how observations of these signatures may be optimized by refining the orbital parameters. Subject headings: planetary systems – techniques: photometric – techniques: radial velocities 1. INTRODUCTION (Knutson et al. 2009b). Examples in the optical include The currently known diversity of exoplanets is greatly Kepler observations of HAT-P-7b (Welsh et al. 2010) and attributable to the revolution of the transit detection phase variations detected in the light curve of CoRoT-1b method over the past 10 years. The measurement of (Snellen et al. 2009). radius and hence density were the first steps from the Kane & von Braun (2008) and Kane & von Braun results of this technique, but soon to follow were atmo- (2009) showed that planets in eccentric orbits have spheric studies from both primary transit and secondary inflated transit probabilities, as demonstrated by eclipse. However, the unknown inclination of the plan- HD 17156b (Barbieri et al. 2007) and HD 80606b etary orbits makes this technique only applicable to a (Laughlin et al. 2009). These types of planets will pro- relatively small fraction of the known exoplanets. For duce relatively high phase amplitudes during a brief pe- the non-transiting planets, reflected light and phase vari- riod (periaston passage) of the orbit. However, phase ations present an additional avenue through which to variations of non-transiting planets have been restricted investigate planetary atmospheres (Charbonneau et al. to hot Jupiters, including υ And b (Harrington et al. 1999; Leigh et al. 2003). The net result of this new in- 2006) and HD 179949b (Cowan et al. 2007). There formation has lead to an unprecedented ability to char- have been searches for phase variations of, for exam- acterize exoplanets. ple, HD 75289Ab (Rodler et al. 2008) and τ Boo b Phase functions in the Infra-Red (IR) primarily mea- (Charbonneau et al. 1999; Rodler et al. 2010) but no sig- sure the thermal properties of the planet whereas op- natures were detected in either case. Exploring the at- tical measurements probe the planetary albedo. The mospheric properties of longer-period planets requires relation between giant planet atmospheres and phase taking advantage of highly-eccentric non-transiting sys- curves have been described in detail by Sudarsky et al. tems. Thus we also constrain the inclination and hence (2005). Iro & Deming (2010) further investigate the the mass of such planets. arXiv:1009.4931v1 [astro-ph.EP] 24 Sep 2010 time-variation of the atmospheres in the IR for eccentric Here we investigate the expected photometric phase planets using radiative transfer models. The phase vari- amplitude of long-period eccentric planets and show how ation of our own solar system has been investigated by planetary orbits in resonance can result in ambiguous Dyudina et al. (2005), and it has been shown that phase phase variation detections. We further apply this anal- functions can be used to produce longitudinal thermal ysis by calculating maximum flux ratios for the known maps of exoplanets (Cowan & Agol 2008). In addition, exoplanets and considering several interesting case stud- phase curves of terrestrial planets have been considered ies. We also determine the effective orbital phase regime by Mallama (2009). over which detectability is maximised and show how re- Phase variations of exoplanets in the IR and op- finement of orbital parameters can allow efficient tar- tical regimes have had success due to increased ac- geted observations at these times. This study is intended cess to improved instrumentation and space-based ob- from an observers point of view in so far as these observ- servatories. This has primarily been investigated for able variations can be reconnected back to the theoretical transiting planets since the edge-on orbital plane pro- models of exoplanetary atmospheres. duces the highest phase amplitude. Examples of ob- served phase variations in the IR (using Spitzer) include 2. EXOPLANET PHASE VARIATIONS HD 189733b (Knutson et al. 2009a) and HD 149026b In this section, we establish the theoretical framework which will be applied in the remainder of the paper, Electronic address: [email protected] similar to the formalism used by Collier Cameron et al. 2 Stephen R. Kane & Dawn M. Gelino 2.1. Wavelength Dependence As noted in the previous section, the observed flux ratio from an exoplanet is wavelength dependent. In particular, the atmospheric composition drives the scat- tering properties and thus the forms of the geometric albedo and phase function. This dependence has been considered in great detail by Sudarsky et al. (2005) in planet α = 0° which they construct empirical models for exoplanet at- mospheres and intergrate over the surface with assumed opacities depending upon atmospheric composition. This thorough analysis is not reproduced here, but we do use the results of their analysis for a restricted wave- α = 90° star length, particularly with regards to the albedo function discuessed in the following sections. Here we confine our α = 270° study to optical wavelengths centered on 550 nm. This ω broadly encompasses the results obtained by such stud- α = 180° ies at Collier Cameron et al. (2002), Leigh et al. (2003), and Rodler et al. (2010). This also places the study near to observer the peak response of the Kepler CCD, the relevance of which will be discussed in later sections. Fig. 1.— Orbit of eccentric planet, showing orbit phase angles corresponding to full (α = 0◦), first quarter (α = 90◦), new (α = 180(2002)◦), and and third more quarter recently (α = by 270 Rodler◦) phases. et al. (2010). Figure 2.2. Geometric Albedo 1 shows a top-down view of an elliptical planetary orbit. It has been shown through atmospheric models that The phase angle α is described by there is a dependence of the geometric albedo of cos α = sin(ω + f) (1) giant planets on the semi-major axis of the orbit where ω is the argument of periastron and f is the true (Sudarsky et al. 2000, 2005; Cahoy et al. 2010). We di- anomaly. The phase angle is defined to be α =0◦ when rect the reader to Figure 9 of Sudarsky et al. (2005) the planet is at superior conjunction (“full” phase). In which details the wavelength and star–planet separation terms of orbital parameters, this location in the orbit dependence of the geometric albedo. Jupiter is known occurs when ω + f = 270◦. to have a visual geometric albedo of ∼ 0.52. However, The flux at wavelength λ incident upon the planet is the strong irradition of the atmospheres of giant planets described by in short-period orbits results in the removal of reflective L (λ) condensates from the upper atmospheres and thus a sig- F (λ)= ⋆ (2) i 4πr2 nificant lowering of the geometric albedo. Observations of HD 209458b using the Microvariability and Oscilla- where L is the luminosity of the star and r is the star– ⋆ tions of STars (MOST) satellite by Rowe et al. (2008) planet separation. This separation is given by failed to detect phase variations and thus they were able a(1 − e2) r = (3) to place an upper limit of Ag < 0.08, subsequently in- 1+ e cos f vestigated using model atmospheres by Burrows et al. where a is the semi-major axis and e is the orbital ec- (2008). More recent observations of HAT-P-7b using Ke- centricity. The geometric albedo of a planet is defined at pler by Welsh et al. (2010) revealed phase variations in α =0◦ as follows the light curve from which they were able to deduce a geomtric albedo of 0.18. Fr(0, λ) Ag(λ)= (4) Through the examples mentioned above, and the con- Fi(λ) sideration of the theoretical models of Sudarsky et al. where Fr is the reflected light from the planet. The plan- (2005), we have constructed a model which approximates etary flux received at Earth is then the albedo of giant planets as a function of star–planet 2 Rp separation (see Equation 3). This is a hyperbolic tan- fp(α, λ)= Ag(λ)g(α, λ)Fi(λ) (5) gential function of the form d2 r−1 −(r−1) where Rp is the planetary radius, d is the distance to the (e − e ) 3 Ag = + (8) star, and g(α, λ) is the phase function. Since the stellar 5(er−1 + e−(r−1)) 10 flux received at Earth is L (λ) Equation 8 is plotted in Figure 2, showing the semi-major f (λ)= ⋆ (6) ⋆ 4πd2 axes of HAT-P-7b and Jupiter for reference. This func- then the flux ratio of the planet to the host star is defined tion well represents the rapid rise in optical albedo be- as tween 0.2 and 1 AU described by Sudarsky et al.
Load more

Recommended publications
  • Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation
    Lurking in the Shadows: Wide-Separation Gas Giants as Tracers of Planet Formation Thesis by Marta Levesque Bryan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2018 Defended May 1, 2018 ii © 2018 Marta Levesque Bryan ORCID: [0000-0002-6076-5967] All rights reserved iii ACKNOWLEDGEMENTS First and foremost I would like to thank Heather Knutson, who I had the great privilege of working with as my thesis advisor. Her encouragement, guidance, and perspective helped me navigate many a challenging problem, and my conversations with her were a consistent source of positivity and learning throughout my time at Caltech. I leave graduate school a better scientist and person for having her as a role model. Heather fostered a wonderfully positive and supportive environment for her students, giving us the space to explore and grow - I could not have asked for a better advisor or research experience. I would also like to thank Konstantin Batygin for enthusiastic and illuminating discussions that always left me more excited to explore the result at hand. Thank you as well to Dimitri Mawet for providing both expertise and contagious optimism for some of my latest direct imaging endeavors. Thank you to the rest of my thesis committee, namely Geoff Blake, Evan Kirby, and Chuck Steidel for their support, helpful conversations, and insightful questions. I am grateful to have had the opportunity to collaborate with Brendan Bowler. His talk at Caltech my second year of graduate school introduced me to an unexpected population of massive wide-separation planetary-mass companions, and lead to a long-running collaboration from which several of my thesis projects were born.
    [Show full text]
  • Naming the Extrasolar Planets
    Naming the extrasolar planets W. Lyra Max Planck Institute for Astronomy, K¨onigstuhl 17, 69177, Heidelberg, Germany [email protected] Abstract and OGLE-TR-182 b, which does not help educators convey the message that these planets are quite similar to Jupiter. Extrasolar planets are not named and are referred to only In stark contrast, the sentence“planet Apollo is a gas giant by their assigned scientific designation. The reason given like Jupiter” is heavily - yet invisibly - coated with Coper- by the IAU to not name the planets is that it is consid- nicanism. ered impractical as planets are expected to be common. I One reason given by the IAU for not considering naming advance some reasons as to why this logic is flawed, and sug- the extrasolar planets is that it is a task deemed impractical. gest names for the 403 extrasolar planet candidates known One source is quoted as having said “if planets are found to as of Oct 2009. The names follow a scheme of association occur very frequently in the Universe, a system of individual with the constellation that the host star pertains to, and names for planets might well rapidly be found equally im- therefore are mostly drawn from Roman-Greek mythology. practicable as it is for stars, as planet discoveries progress.” Other mythologies may also be used given that a suitable 1. This leads to a second argument. It is indeed impractical association is established. to name all stars. But some stars are named nonetheless. In fact, all other classes of astronomical bodies are named.
    [Show full text]
  • Download This Article in PDF Format
    A&A 562, A92 (2014) Astronomy DOI: 10.1051/0004-6361/201321493 & c ESO 2014 Astrophysics Li depletion in solar analogues with exoplanets Extending the sample, E. Delgado Mena1,G.Israelian2,3, J. I. González Hernández2,3,S.G.Sousa1,2,4, A. Mortier1,4,N.C.Santos1,4, V. Zh. Adibekyan1, J. Fernandes5, R. Rebolo2,3,6,S.Udry7, and M. Mayor7 1 Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal e-mail: [email protected] 2 Instituto de Astrofísica de Canarias, C/ Via Lactea s/n, 38200 La Laguna, Tenerife, Spain 3 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain 4 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, 4169-007 Porto, Portugal 5 CGUC, Department of Mathematics and Astronomical Observatory, University of Coimbra, 3049 Coimbra, Portugal 6 Consejo Superior de Investigaciones Científicas, CSIC, Spain 7 Observatoire de Genève, Université de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland Received 18 March 2013 / Accepted 25 November 2013 ABSTRACT Aims. We want to study the effects of the formation of planets and planetary systems on the atmospheric Li abundance of planet host stars. Methods. In this work we present new determinations of lithium abundances for 326 main sequence stars with and without planets in the Teff range 5600–5900 K. The 277 stars come from the HARPS sample, the remaining targets were observed with a variety of high-resolution spectrographs. Results. We confirm significant differences in the Li distribution of solar twins (Teff = T ± 80 K, log g = log g ± 0.2and[Fe/H] = [Fe/H] ±0.2): the full sample of planet host stars (22) shows Li average values lower than “single” stars with no detected planets (60).
    [Show full text]
  • Arxiv:2105.11583V2 [Astro-Ph.EP] 2 Jul 2021 Keck-HIRES, APF-Levy, and Lick-Hamilton Spectrographs
    Draft version July 6, 2021 Typeset using LATEX twocolumn style in AASTeX63 The California Legacy Survey I. A Catalog of 178 Planets from Precision Radial Velocity Monitoring of 719 Nearby Stars over Three Decades Lee J. Rosenthal,1 Benjamin J. Fulton,1, 2 Lea A. Hirsch,3 Howard T. Isaacson,4 Andrew W. Howard,1 Cayla M. Dedrick,5, 6 Ilya A. Sherstyuk,1 Sarah C. Blunt,1, 7 Erik A. Petigura,8 Heather A. Knutson,9 Aida Behmard,9, 7 Ashley Chontos,10, 7 Justin R. Crepp,11 Ian J. M. Crossfield,12 Paul A. Dalba,13, 14 Debra A. Fischer,15 Gregory W. Henry,16 Stephen R. Kane,13 Molly Kosiarek,17, 7 Geoffrey W. Marcy,1, 7 Ryan A. Rubenzahl,1, 7 Lauren M. Weiss,10 and Jason T. Wright18, 19, 20 1Cahill Center for Astronomy & Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA 2IPAC-NASA Exoplanet Science Institute, Pasadena, CA 91125, USA 3Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, Stanford, CA 94305, USA 4Department of Astronomy, University of California Berkeley, Berkeley, CA 94720, USA 5Cahill Center for Astronomy & Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA 6Department of Astronomy & Astrophysics, The Pennsylvania State University, 525 Davey Lab, University Park, PA 16802, USA 7NSF Graduate Research Fellow 8Department of Physics & Astronomy, University of California Los Angeles, Los Angeles, CA 90095, USA 9Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA 91125, USA 10Institute for Astronomy, University of Hawai`i,
    [Show full text]
  • Biosignatures Search in Habitable Planets
    galaxies Review Biosignatures Search in Habitable Planets Riccardo Claudi 1,* and Eleonora Alei 1,2 1 INAF-Astronomical Observatory of Padova, Vicolo Osservatorio, 5, 35122 Padova, Italy 2 Physics and Astronomy Department, Padova University, 35131 Padova, Italy * Correspondence: [email protected] Received: 2 August 2019; Accepted: 25 September 2019; Published: 29 September 2019 Abstract: The search for life has had a new enthusiastic restart in the last two decades thanks to the large number of new worlds discovered. The about 4100 exoplanets found so far, show a large diversity of planets, from hot giants to rocky planets orbiting small and cold stars. Most of them are very different from those of the Solar System and one of the striking case is that of the super-Earths, rocky planets with masses ranging between 1 and 10 M⊕ with dimensions up to twice those of Earth. In the right environment, these planets could be the cradle of alien life that could modify the chemical composition of their atmospheres. So, the search for life signatures requires as the first step the knowledge of planet atmospheres, the main objective of future exoplanetary space explorations. Indeed, the quest for the determination of the chemical composition of those planetary atmospheres rises also more general interest than that given by the mere directory of the atmospheric compounds. It opens out to the more general speculation on what such detection might tell us about the presence of life on those planets. As, for now, we have only one example of life in the universe, we are bound to study terrestrial organisms to assess possibilities of life on other planets and guide our search for possible extinct or extant life on other planetary bodies.
    [Show full text]
  • Dynamical Stability and Habitability of a Terrestrial Planet in HD74156
    A dynamic search for potential habitable planets amongst the extrasolar planets 1,2 1 1 1,3 1, 4 P. Hinds , A. Munro , S. T. Maddison , C. Tan , and M. C. Gino [1] Swinburne University, Australia [2] Pierce College, USA [3] Methodist Ladies’ College, Australia [4] Dudley Observatory, USA ABSTRACT: While the detection of habitable terrestrial planets around nearby stars is currently beyond our observational capabilities, dynamical studies can help us locate potential candidates. Following from the work of Menou & Tabachnik (2003), we use a symplectic integrator to search for potential stable terrestrial planetary orbits in the habitable zones of known extrasolar planetary systems. A swarm of massless test particles is initially used to identify stability zones, and then an Earth-mass planet is placed within these zones to investigate their dynamical stability. We investigate 22 new systems discovered since the work of Menou & Tabachnik, as well as simulate some of the previous 85 extrasolar systems whose orbital parameters have been more precisely constrained. In particular, we model three systems that are now confirmed or potential double planetary systems: HD169830, HD160691 and eps Eridani. The results of these dynamical studies can be used as a potential target list for the Terrestrial Planet Finder. Introduction Numerical Technique Results & Discussion To date 122 extrasolar planets have been detected around 107 stars, with 13 of them To follow the evolution of the planetary systems, we use the SWIFT integration software package1. This The systems we have investigated broadly fall in four categories: (1) unstable being multiple planet systems (Schneider, 2004). Observational evidence for the allows us to model a planetary system and a swarm of massless test particles in orbit around a central star.
    [Show full text]
  • Arxiv:0809.1275V2
    How eccentric orbital solutions can hide planetary systems in 2:1 resonant orbits Guillem Anglada-Escud´e1, Mercedes L´opez-Morales1,2, John E. Chambers1 [email protected], [email protected], [email protected] ABSTRACT The Doppler technique measures the reflex radial motion of a star induced by the presence of companions and is the most successful method to detect ex- oplanets. If several planets are present, their signals will appear combined in the radial motion of the star, leading to potential misinterpretations of the data. Specifically, two planets in 2:1 resonant orbits can mimic the signal of a sin- gle planet in an eccentric orbit. We quantify the implications of this statistical degeneracy for a representative sample of the reported single exoplanets with available datasets, finding that 1) around 35% percent of the published eccentric one-planet solutions are statistically indistinguishible from planetary systems in 2:1 orbital resonance, 2) another 40% cannot be statistically distinguished from a circular orbital solution and 3) planets with masses comparable to Earth could be hidden in known orbital solutions of eccentric super-Earths and Neptune mass planets. Subject headings: Exoplanets – Orbital dynamics – Planet detection – Doppler method arXiv:0809.1275v2 [astro-ph] 25 Nov 2009 Introduction Most of the +300 exoplanets found to date have been discovered using the Doppler tech- nique, which measures the reflex motion of the host star induced by the planets (Mayor & Queloz 1995; Marcy & Butler 1996). The diverse characteristics of these exoplanets are somewhat surprising. Many of them are similar in mass to Jupiter, but orbit much closer to their 1Carnegie Institution of Washington, Department of Terrestrial Magnetism, 5241 Broad Branch Rd.
    [Show full text]
  • Arxiv:1512.00417V1 [Astro-Ph.EP] 1 Dec 2015 Velocity Surveys
    Draft version December 2, 2015 Preprint typeset using LATEX style emulateapj v. 5/2/11 THE LICK-CARNEGIE EXOPLANET SURVEY: HD 32963 { A NEW JUPITER ANALOG ORBITING A SUN-LIKE STAR Dominick Rowan 1, Stefano Meschiari 2, Gregory Laughlin3, Steven S. Vogt3, R. Paul Butler4,Jennifer Burt3, Songhu Wang3,5, Brad Holden3, Russell Hanson3, Pamela Arriagada4, Sandy Keiser4, Johanna Teske4, Matias Diaz6 Draft version December 2, 2015 ABSTRACT We present a set of 109 new, high-precision Keck/HIRES radial velocity (RV) observations for the solar-type star HD 32963. Our dataset reveals a candidate planetary signal with a period of 6.49 ± 0.07 years and a corresponding minimum mass of 0.7 ± 0.03 Jupiter masses. Given Jupiter's crucial role in shaping the evolution of the early Solar System, we emphasize the importance of long-term radial velocity surveys. Finally, using our complete set of Keck radial velocities and correcting for the relative detectability of synthetic planetary candidates orbiting each of the 1,122 stars in our sample, we estimate the frequency of Jupiter analogs across our survey at approximately 3%. Subject headings: Extrasolar Planets, Data Analysis and Techniques 1. INTRODUCTION which favors short-period planets. The past decade has witnessed an astounding acceler- Given the importance of Jupiter in the dynamical his- ation in the rate of exoplanet detections, thanks in large tory of our Solar System, the presence of a Jupiter ana- part to the advent of the Kepler mission. As of this writ- log is likely to be a crucial differentiator for exoplanetary ing, more than 1,500 confirmed planetary candidates are systems.
    [Show full text]
  • The ELODIE Survey for Northern Extra-Solar Planets?,??,???
    A&A 410, 1039–1049 (2003) Astronomy DOI: 10.1051/0004-6361:20031340 & c ESO 2003 Astrophysics The ELODIE survey for northern extra-solar planets?;??;??? I. Six new extra-solar planet candidates C. Perrier1,J.-P.Sivan2,D.Naef3,J.L.Beuzit1, M. Mayor3,D.Queloz3,andS.Udry3 1 Laboratoire d’Astrophysique de Grenoble, Universit´e J. Fourier, BP 53, 38041 Grenoble, France 2 Observatoire de Haute-Provence, 04870 St-Michel L’Observatoire, France 3 Observatoire de Gen`eve, 51 Ch. des Maillettes, 1290 Sauverny, Switzerland Received 17 July 2002 / Accepted 1 August 2003 Abstract. Precise radial-velocity observations at Haute-Provence Observatory (OHP, France) with the ELODIE echelle spec- trograph have been undertaken since 1994. In addition to several discoveries described elsewhere, including and following that of 51 Peg b, they reveal new sub-stellar companions with essentially moderate to long periods. We report here about such companions orbiting five solar-type stars (HD 8574, HD 23596, HD 33636, HD 50554, HD 106252) and one sub-giant star (HD 190228). The companion of HD 8574 has an intermediate period of 227.55 days and a semi-major axis of 0.77 AU. All other companions have long periods, exceeding 3 years, and consequently their semi-major axes are around or above 2 AU. The detected companions have minimum masses m2 sin i ranging from slightly more than 2 MJup to 10.6 MJup. These additional objects reinforce the conclusion that most planetary companions have masses lower than 5 MJup but with a tail of the mass dis- tribution going up above 15 MJup.
    [Show full text]
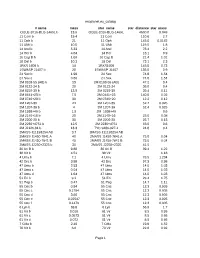
  • Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
    exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55
    [Show full text]
  • Virgo the Virgin
    Virgo the Virgin Virgo is one of the constellations of the zodiac, the group tion Virgo itself. There is also the connection here with of 12 constellations that lies on the ecliptic plane defined “The Scales of Justice” and the sign Libra which lies next by the planets orbital orientation around the Sun. Virgo is to Virgo in the Zodiac. The study of astronomy had a one of the original 48 constellations charted by Ptolemy. practical “time keeping” aspect in the cultures of ancient It is the largest constellation of the Zodiac and the sec- history and as the stars of Virgo appeared before sunrise ond - largest constellation after Hydra. Virgo is bordered by late in the northern summer, many cultures linked this the constellations of Bootes, Coma Berenices, Leo, Crater, asterism with crops, harvest and fecundity. Corvus, Hydra, Libra and Serpens Caput. The constella- tion of Virgo is highly populated with galaxies and there Virgo is usually depicted with angel - like wings, with an are several galaxy clusters located within its boundaries, ear of wheat in her left hand, marked by the bright star each of which is home to hundreds or even thousands of Spica, which is Latin for “ear of grain”, and a tall blade of galaxies. The accepted abbreviation when enumerating grass, or a palm frond, in her right hand. Spica will be objects within the constellation is Vir, the genitive form is important for us in navigating Virgo in the modern night Virginis and meteor showers that appear to originate from sky. Spica was most likely the star that helped the Greek Virgo are called Virginids.
    [Show full text]
  • A Search for the Transit of HD 168443B: Improved Orbital
    Submitted for publication in the Astrophysical Journal A Search for the Transit of HD 168443b: Improved Orbital Parameters and Photometry Genady Pilyavsky1, Suvrath Mahadevan1,2, Stephen R. Kane3, Andrew W. Howard4,5, David R. Ciardi3, Chris de Pree6, Diana Dragomir3,7, Debra Fischer8, Gregory W. Henry9, Eric L. N. Jensen10, Gregory Laughlin11, Hannah Marlowe6, Markus Rabus12, Kaspar von Braun3, Jason T. Wright1,2, Xuesong X. Wang1 [email protected] [email protected] ABSTRACT The discovery of transiting planets around bright stars holds the potential to greatly enhance our understanding of planetary atmospheres. In this work 1Department of Astronomy and Astrophysics, Pennsylvania State University, 525 Davey Laboratory, University Park, PA 16802 2Center for Exoplanets & Habitable Worlds, Pennsylvania State University, 525 Davey Laboratory, Uni- versity Park, PA 16802 3NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue, Pasadena, CA 91125 4Department of Astronomy, University of California, Berkeley, CA 94720 5Space Sciences Laboratory, University of California, Berkeley, CA 94720 6Department of Physics and Astronomy, Agnes Scott College, 141 East College Avenue, Decatur, GA arXiv:1109.5166v1 [astro-ph.EP] 23 Sep 2011 30030, USA 7Department of Physics & Astronomy, University of British Columbia, Vancouver, BC V6T1Z1, Canada 8Department of Astronomy, Yale University, New Haven, CT 06511 9Center of Excellence in Information Systems, Tennessee State University, 3500 John A. Merritt Blvd., Box 9501, Nashville, TN 37209 10Dept of Physics & Astronomy, Swarthmore College, Swarthmore, PA 19081 11UCO/Lick Observatory, University of California, Santa Cruz, CA 95064 12Departamento de Astonom´ıay Astrof´ısica, Pontificia Universidad Cat´olica de Chile, Casilla 306, Santiago 22, Chile –2– we present the search for transits of HD168443b, a massive planet orbiting the bright star HD 168443 (V =6.92) with a period of 58.11 days.
    [Show full text]