DOCSLIB.ORG

Polygons, Polyhedra, and Polytopes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polygons, Polyhedra, and Polytopes Polygons, Polyhedra, and Polytopes Marco Gualtieri Department of Mathematics, University of Toronto Warm-up: Polygons A polygon is a region of the plane whose border is a path made up of straight line segments which only touch at endpoints (called vertices). We say the polygon is convex when it \bulges out": a line joining two points in the polygon never leaves the polygon. Regular Polygons We say that a convex polygon is regular when all its sides have the same length and all the angles are the same. f3g f4g f5g f6g f7g f8g We can focus on the interior of the polygon, which is 2-dimensional, or on its boundary, which has dimension 1. Regular Polygons: Calculation To compute the angles, drive around the polygon { you will turn n times, each time by 1=n of a full turn. For a pentagon, the interior angle is 3=10 of a full turn, i.e. 108◦. Polyhedra A Polyhedron is a region of 3D space with boundary made entirely of polygons (called the faces), which may touch only by sharing an entire edge. We want only convex polyhedra: a line joining two points in the polyhedron must be completely contained in it. Also we want regular polyhedra: this means that the faces are all the same regular polygon and the vertices are all identical. Regular Polyhedra If the faces are p-gons, and there are q around a vertex, then 1 1 1 1 each contributes an angle 2 − p , for a total of q( 2 − p ). But this must be less than a full turn (or the vertex would be flat), so: 1 1 1 + > q p 2 Faces used Solution Schl¨aflisymbol Triangles (p = 3) q = 3, 4, 5 f3,3g, f3,4g,f3,5g Squares (p = 4) q = 3 f4,3g Pentagons (p = 5) q = 3 f5,3g f3,3g: Tetrahedron If we assemble three regular triangles we see that the free edges form another regular triangle, so we can glue in a fourth triangle to get a f3; 3g. This is the Tetrahedron. I Show that non-intersecting edges are perpendicular. I Show that the angle between two faces is cos−1(1=3) ≈ 70:5◦. f3,4g: Octahedron The height of a pyramid on a square can be adjusted until the triangles are regular. Then two of these placed base to base gives a polyhedron where every vertex has four regular triangles: it's a f3; 4g. This is the Octahedron. In Cartesian coordinates the vertices are (±1; 0; 0); (0; ±1; 0); (0; 0; ±1): Looking at the following picture, we see that the dihedral angle of the octahedron and tetrahedron sum to a 1=2 turn, giving ≈ 109:47◦ for octahedron. f3,5g: Icosahedron By adjusting the height of a pyramid on a pentagon, we get five regular triangles to a single vertex. Then observe that two of these can be glued on an antiprism: This forms a f3; 5g: the Icosahedron (twenty \seats" or faces). It has dihedral angle ≈ 138:19◦ f4,3g: Cube Finally we get to the cube, which is just a prism on a square: each vertex has three squares. Dihedral angle is 90◦. The cube may also be constructed as the dual of the octahedron. It may also be synthesized as a hydrocarbon C8H8 called cubane. f5,3g: Dodecahedron To build f5; 3g, assemble a \bowl" of six pentagons and show that the free vertices have the same distance from the central axis. This shows that two such bowls may be glued together. Alternatively, it is the dual to the icosahedron. The vertices have the following coordinates: (±1; ±1; ±1); (0; ±φ−1; ±φ); (±φ−1; ±φ, 0); (±φ, 0; ±φ−1); p 1+ 5 where φ = 2 is the golden ratio. The dihedral angle is 2 tan−1(φ) ≈ 116:57◦. Of course, it has also recently been synthesized as Dodecahedrane C20H20. Polyhedra Summary Regular Polytopes An n-polytope is region in n-dimensional space with boundary made entirely of n − 1-polytopes (called the faces), which may touch only by sharing an entire one of their own faces. We focus on convex polytopes which are also regular, which means they have the greatest possible symmetry: any way of picking a face, and then a face of that face, continuing down to a point, is equivalent to any other. A note about visualization: When imagining a 4-d polytope, it is useful to concentrate on its 3-d boundary: this is a bunch of 3-d polyhedra which are glued together along their 2-d faces. Recall that we sometimes describe 3-d polyhedra by describing their 2-d surface. The most obvious case of this is its net, a collection of planar polygons which folds to give the surface of the polyhedron. The net of a polytope is a collection of polyhedra glued along their faces: the result is the 3-d boundary of the 4-d polytope. Another strategy we use for polyhedra is to project the boundary surface to 2-d with transparent faces. We obtain a diagram of overlapping 2-d polygons which show how the polygons on the boundary are glued together. On the left, we understand how two of the overlapping squares are glued along an edge to make part of the boundary of a 3-d cube. On the right, we see how three of the overlapping cubes make part of the boundary of a 4-d cube. Note that this is possible because the dihedral angle of the cube is 90◦, so three of them come together to make a convex edge. Possible 4-polytopes The constraint that the dihedral angle must sum to less than a full turn at an edge classifies polytopes in dimension 4. Faces used Dihed. angle # at each edge Schl¨afli Tetra. (f3,3g) 70:53◦ 3,4,5 f3,3,3g, f3,3,4g,f3,3,5g Octa. (f3,4g) 109:47◦ 3 f3,4,3g Icos. (f3,5g) 138:19◦ none Cubes (f4,3g) 90◦ 3 f4,3,3g Dodec. (f5,3g) 116:57◦ 3 f5,3,3g All 6 of these possibilities are realized by an actual polytope, and these were first classified by Schl¨afli. f3,3,3g, f3,3,4g, and f4,3,3g These three polytopes exist in all dimensions: they are the Simplex, the Cross polytope and the Hypercube. The n-simplex is a pyramid over the n − 1 simplex, the n-cross is a double pyramid over the (n − 1)-cross, and the n-cube is a prism over the (n − 1)-cube. f3,3,5g: The 600-cell There is only one way of combining tetrahedra, five to an edge. The result involves 600 tetrahedra, 1200 triangular faces, 720 edges and 120 vertices. f3,4,3g: The 24-cell f3; 4; 3g is a 4-polytope whose boundary is composed of 24 octahedra joined 3 to an edge. There are 96 edges, 96 triangles, and 24 vertices (it is self-dual, like the simplex). f5,3,3g: The 120-cell The last exotic regular 4-polytope is the 120-cell, whose boundary has 120 dodecahedra joined 3 to an edge. It is dual to the 600-cell. (for the regular polytopes and the slides!) For more information, consult I Regular Polytopes, by H. S. M. Coxeter. I Geometric Folding Algorithms, by Demaine and O'Rourke. I Wikipedia's extensive Polytope data..
Load more

Recommended publications
  • Geometry of Generalized Permutohedra
    Geometry of Generalized Permutohedra by Jeffrey Samuel Doker A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Mathematics in the Graduate Division of the University of California, Berkeley Committee in charge: Federico Ardila, Co-chair Lior Pachter, Co-chair Matthias Beck Bernd Sturmfels Lauren Williams Satish Rao Fall 2011 Geometry of Generalized Permutohedra Copyright 2011 by Jeffrey Samuel Doker 1 Abstract Geometry of Generalized Permutohedra by Jeffrey Samuel Doker Doctor of Philosophy in Mathematics University of California, Berkeley Federico Ardila and Lior Pachter, Co-chairs We study generalized permutohedra and some of the geometric properties they exhibit. We decompose matroid polytopes (and several related polytopes) into signed Minkowski sums of simplices and compute their volumes. We define the associahedron and multiplihe- dron in terms of trees and show them to be generalized permutohedra. We also generalize the multiplihedron to a broader class of generalized permutohedra, and describe their face lattices, vertices, and volumes. A family of interesting polynomials that we call composition polynomials arises from the study of multiplihedra, and we analyze several of their surprising properties. Finally, we look at generalized permutohedra of different root systems and study the Minkowski sums of faces of the crosspolytope. i To Joe and Sue ii Contents List of Figures iii 1 Introduction 1 2 Matroid polytopes and their volumes 3 2.1 Introduction . .3 2.2 Matroid polytopes are generalized permutohedra . .4 2.3 The volume of a matroid polytope . .8 2.4 Independent set polytopes . 11 2.5 Truncation flag matroids . 14 3 Geometry and generalizations of multiplihedra 18 3.1 Introduction .
    [Show full text]
  • Lecture 3 1 Geometry of Linear Programs
    ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1.
    [Show full text]
  • Two Poset Polytopes
    Discrete Comput Geom 1:9-23 (1986) G eometrv)i.~.reh, ~ ( :*mllmlati~ml © l~fi $1~ter-Vtrlq New Yorklu¢. t¢ Two Poset Polytopes Richard P. Stanley* Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139 Abstract. Two convex polytopes, called the order polytope d)(P) and chain polytope <~(P), are associated with a finite poset P. There is a close interplay between the combinatorial structure of P and the geometric structure of E~(P). For instance, the order polynomial fl(P, m) of P and Ehrhart poly- nomial i(~9(P),m) of O(P) are related by f~(P,m+l)=i(d)(P),m). A "transfer map" then allows us to transfer properties of O(P) to W(P). In particular, we transfer known inequalities involving linear extensions of P to some new inequalities. I. The Order Polytope Our aim is to investigate two convex polytopes associated with a finite partially ordered set (poset) P. The first of these, which we call the "order polytope" and denote by O(P), has been the subject of considerable scrutiny, both explicit and implicit, Much of what we say about the order polytope will be essentially a review of well-known results, albeit ones scattered throughout the literature, sometimes in a rather obscure form. The second polytope, called the "chain polytope" and denoted if(P), seems never to have been previously considered per se. It is a special case of the vertex-packing polytope of a graph (see Section 2) but has many special properties not in general valid or meaningful for graphs.
    [Show full text]
  • Compact Hyperbolic Tetrahedra with Non-Obtuse Dihedral Angles
    Compact hyperbolic tetrahedra with non-obtuse dihedral angles Roland K. W. Roeder ∗ January 7, 2006 Abstract Given a combinatorial description C of a polyhedron having E edges, the space of dihedral angles of all compact hyperbolic polyhe- dra that realize C is generally not a convex subset of RE [9]. If C has five or more faces, Andreev’s Theorem states that the correspond- ing space of dihedral angles AC obtained by restricting to non-obtuse angles is a convex polytope. In this paper we explain why Andreev did not consider tetrahedra, the only polyhedra having fewer than five faces, by demonstrating that the space of dihedral angles of com- pact hyperbolic tetrahedra, after restricting to non-obtuse angles, is non-convex. Our proof provides a simple example of the “method of continuity”, the technique used in classification theorems on polyhe- dra by Alexandrow [4], Andreev [5], and Rivin-Hodgson [19]. 2000 Mathematics Subject Classification. 52B10, 52A55, 51M09. Key Words. Hyperbolic geometry, polyhedra, tetrahedra. Given a combinatorial description C of a polyhedron having E edges, the space of dihedral angles of all compact hyperbolic polyhedra that realize C is generally not a convex subset of RE. This is proved in a nice paper by D´ıaz [9]. However, Andreev’s Theorem [5, 13, 14, 20] shows that by restricting to compact hyperbolic polyhedra with non-obtuse dihedral angles, E the space of dihedral angles is a convex polytope, which we label AC R . It is interesting to note that the statement of Andreev’s Theorem requires⊂ ∗rroeder@fields.utoronto.ca 1 that C have five or more faces, ruling out the tetrahedron which is the only polyhedron having fewer than five faces.
    [Show full text]
  • Using Information Theory to Discover Side Chain Rotamer Classes
    Pacific Symposium on Biocomputing 4:278-289 (1999) U S I N G I N F O R M A T I O N T H E O R Y T O D I S C O V E R S I D E C H A I N R O T A M E R C L A S S E S : A N A L Y S I S O F T H E E F F E C T S O F L O C A L B A C K B O N E S T R U C T U R E J A C Q U E L Y N S . F E T R O W G E O R G E B E R G Department of Molecular Biology Department of Computer Science The Scripps Research Institute University at Albany, SUNY La Jolla, CA 92037, USA Albany, NY 12222, USA An understanding of the regularities in the side chain conformations of proteins and how these are related to local backbone structures is important for protein modeling and design. Previous work using regular secondary structures and regular divisions of the backbone dihedral angle data has shown that these rotamers are sensitive to the protein’s local backbone conformation. In this preliminary study, we demonstrate a method for combining a more general backbone structure model with an objective clustering algorithm to investigate the effects of backbone structures on side chain rotamer classes and distributions. For the local structure classification, we use the Structural Building Blocks (SBB) categories, which represent all types of secondary structure, including regular structures, capping structures, and loops.
    [Show full text]
  • 1 Lifts of Polytopes
    Lecture 5: Lifts of polytopes and non-negative rank CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Lifts of polytopes 1.1 Polytopes and inequalities Recall that the convex hull of a subset X n is defined by ⊆ conv X λx + 1 λ x0 : x; x0 X; λ 0; 1 : ( ) f ( − ) 2 2 [ ]g A d-dimensional convex polytope P d is the convex hull of a finite set of points in d: ⊆ P conv x1;:::; xk (f g) d for some x1;:::; xk . 2 Every polytope has a dual representation: It is a closed and bounded set defined by a family of linear inequalities P x d : Ax 6 b f 2 g for some matrix A m d. 2 × Let us define a measure of complexity for P: Define γ P to be the smallest number m such that for some C s d ; y s ; A m d ; b m, we have ( ) 2 × 2 2 × 2 P x d : Cx y and Ax 6 b : f 2 g In other words, this is the minimum number of inequalities needed to describe P. If P is full- dimensional, then this is precisely the number of facets of P (a facet is a maximal proper face of P). Thinking of γ P as a measure of complexity makes sense from the point of view of optimization: Interior point( methods) can efficiently optimize linear functions over P (to arbitrary accuracy) in time that is polynomial in γ P . ( ) 1.2 Lifts of polytopes Many simple polytopes require a large number of inequalities to describe.
    [Show full text]
  • Uniform Polychora
    BRIDGES Mathematical Connections in Art, Music, and Science Uniform Polychora Jonathan Bowers 11448 Lori Ln Tyler, TX 75709 E-mail: [email protected] Abstract Like polyhedra, polychora are beautiful aesthetic structures - with one difference - polychora are four dimensional. Although they are beyond human comprehension to visualize, one can look at various projections or cross sections which are three dimensional and usually very intricate, these make outstanding pieces of art both in model form or in computer graphics. Polygons and polyhedra have been known since ancient times, but little study has gone into the next dimension - until recently. Definitions A polychoron is basically a four dimensional "polyhedron" in the same since that a polyhedron is a three dimensional "polygon". To be more precise - a polychoron is a 4-dimensional "solid" bounded by cells with the following criteria: 1) each cell is adjacent to only one other cell for each face, 2) no subset of cells fits criteria 1, 3) no two adjacent cells are corealmic. If criteria 1 fails, then the figure is degenerate. The word "polychoron" was invented by George Olshevsky with the following construction: poly = many and choron = rooms or cells. A polytope (polyhedron, polychoron, etc.) is uniform if it is vertex transitive and it's facets are uniform (a uniform polygon is a regular polygon). Degenerate figures can also be uniform under the same conditions. A vertex figure is the figure representing the shape and "solid" angle of the vertices, ex: the vertex figure of a cube is a triangle with edge length of the square root of 2.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
  • Digital Geometry Processing Mesh Basics
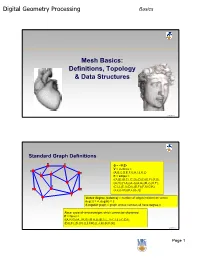
    Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph ©
    [Show full text]
  • Can Every Face of a Polyhedron Have Many Sides ?
    Can Every Face of a Polyhedron Have Many Sides ? Branko Grünbaum Dedicated to Joe Malkevitch, an old friend and colleague, who was always partial to polyhedra Abstract. The simple question of the title has many different answers, depending on the kinds of faces we are willing to consider, on the types of polyhedra we admit, and on the symmetries we require. Known results and open problems about this topic are presented. The main classes of objects considered here are the following, listed in increasing generality: Faces: convex n-gons, starshaped n-gons, simple n-gons –– for n ≥ 3. Polyhedra (in Euclidean 3-dimensional space): convex polyhedra, starshaped polyhedra, acoptic polyhedra, polyhedra with selfintersections. Symmetry properties of polyhedra P: Isohedron –– all faces of P in one orbit under the group of symmetries of P; monohedron –– all faces of P are mutually congru- ent; ekahedron –– all faces have of P the same number of sides (eka –– Sanskrit for "one"). If the number of sides is k, we shall use (k)-isohedron, (k)-monohedron, and (k)- ekahedron, as appropriate. We shall first describe the results that either can be found in the literature, or ob- tained by slight modifications of these. Then we shall show how two systematic ap- proaches can be used to obtain results that are better –– although in some cases less visu- ally attractive than the old ones. There are many possible combinations of these classes of faces, polyhedra and symmetries, but considerable reductions in their number are possible; we start with one of these, which is well known even if it is hard to give specific references for precisely the assertion of Theorem 1.
    [Show full text]
  • Predicting Backbone Cα Angles and Dihedrals from Protein Sequences by Stacked Sparse Auto-Encoder Deep Neural Network
    Predicting backbone C# angles and dihedrals from protein sequences by stacked sparse auto-encoder deep neural network Author Lyons, James, Dehzangi, Abdollah, Heffernan, Rhys, Sharma, Alok, Paliwal, Kuldip, Sattar, Abdul, Zhou, Yaoqi, Yang, Yuedong Published 2014 Journal Title Journal of Computational Chemistry DOI https://doi.org/10.1002/jcc.23718 Copyright Statement © 2014 Wiley Periodicals, Inc.. This is the accepted version of the following article: Predicting backbone Ca angles and dihedrals from protein sequences by stacked sparse auto-encoder deep neural network Journal of Computational Chemistry, Vol. 35(28), 2014, pp. 2040-2046, which has been published in final form at dx.doi.org/10.1002/jcc.23718. Downloaded from http://hdl.handle.net/10072/64247 Griffith Research Online https://research-repository.griffith.edu.au Predicting backbone Cα angles and dihedrals from protein sequences by stacked sparse auto-encoder deep neural network James Lyonsa, Abdollah Dehzangia,b, Rhys Heffernana, Alok Sharmaa,c, Kuldip Paliwala , Abdul Sattara,b, Yaoqi Zhoud*, Yuedong Yang d* aInstitute for Integrated and Intelligent Systems, Griffith University, Brisbane, Australia bNational ICT Australia (NICTA), Brisbane, Australia cSchool of Engineering and Physics, University of the South Pacific, Private Mail Bag, Laucala Campus, Suva, Fiji dInstitute for Glycomics and School of Information and Communication Technique, Griffith University, Parklands Dr. Southport, QLD 4222, Australia *Corresponding authors ([email protected], [email protected]) ABSTRACT Because a nearly constant distance between two neighbouring Cα atoms, local backbone structure of proteins can be represented accurately by the angle between Cαi-1−Cαi−Cαi+1 (θ) and a dihedral angle rotated about the Cαi−Cαi+1 bond (τ).
    [Show full text]
  • Arxiv:1705.01294V1
    Branes and Polytopes Luca Romano email address: [email protected] ABSTRACT We investigate the hierarchies of half-supersymmetric branes in maximal supergravity theories. By studying the action of the Weyl group of the U-duality group of maximal supergravities we discover a set of universal algebraic rules describing the number of independent 1/2-BPS p-branes, rank by rank, in any dimension. We show that these relations describe the symmetries of certain families of uniform polytopes. This induces a correspondence between half-supersymmetric branes and vertices of opportune uniform polytopes. We show that half-supersymmetric 0-, 1- and 2-branes are in correspondence with the vertices of the k21, 2k1 and 1k2 families of uniform polytopes, respectively, while 3-branes correspond to the vertices of the rectified version of the 2k1 family. For 4-branes and higher rank solutions we find a general behavior. The interpretation of half- supersymmetric solutions as vertices of uniform polytopes reveals some intriguing aspects. One of the most relevant is a triality relation between 0-, 1- and 2-branes. arXiv:1705.01294v1 [hep-th] 3 May 2017 Contents Introduction 2 1 Coxeter Group and Weyl Group 3 1.1 WeylGroup........................................ 6 2 Branes in E11 7 3 Algebraic Structures Behind Half-Supersymmetric Branes 12 4 Branes ad Polytopes 15 Conclusions 27 A Polytopes 30 B Petrie Polygons 30 1 Introduction Since their discovery branes gained a prominent role in the analysis of M-theories and du- alities [1]. One of the most important class of branes consists in Dirichlet branes, or D-branes. D-branes appear in string theory as boundary terms for open strings with mixed Dirichlet-Neumann boundary conditions and, due to their tension, scaling with a negative power of the string cou- pling constant, they are non-perturbative objects [2].
    [Show full text]