Risk Analysis for Flood-Control Structure Under Consideration Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Taipei City Voluntary Local Review
Sep. 2020 Sep. 2020 Table Of Contents Mayor Ko’s Preface 05 COVID-19 Pandemic and the Sustainable Development Actions of the City 08 Executive Summary 16 Visions and Goals 22 Policies and Environment 26 Background and Methodology 30 Priority Promotion Goals and Outcomes 36 Future Prospects 106 Appendix 110 2020 Taipei City Voluntary Local Review Mayor Ko’s Preface In line with the international trend of differences and different religious cultures, sustainable development, Taipei City has built a and remain friendly to foreigners and migrant common language and tighter partnership with workers. We deeply believe that only by building global cities. We follow the United Nations’ a tolerant and inclusive society can bring up a framework of Sustainable Development Goals sustainable city with shared prosperity. (SDGs) and combine the city government’s The global outbreak of the Severe Pneumonia Strategic Map for the governance vision and with Novel Pathogens (COVID-19) in 2020 has guidelines toward 2030. The first report of Taipei impacted the world’s sustainable development. City Voluntary Local Review (VLR) was published Epidemic prevention must be facilitated with the in 2019. To tackle the all-around challenges of cooperation of central and local governments. sustainable development for environment, society, Taipei City has taken epidemic prevention and economy more proactively, Taipei City measures in advanced, including quarantine continues and expands the review concerning a hotels, disease prevention taxis, online learning total of 11 SDGs this year. These improve our systems, disaster relief volunteers, and face review of the city’s sustainability, publishing the masks vending machines. On the other hand, 2020 Taipei City VLR. -

Special Act Governing the Management of Keelung River Basin
12/17/2017 經濟部水利署全球資訊網 Water Resources Agency, Ministry of Economic Affairs ::: ::: Laws ::: Home (/) / Laws (/7618/7669/) / Laws and Regulations (/7618/7669/7742/) Laws and Regulations Special Act Governing the Management of Keelung River Basin Promulgation History A total of eight articles promulgated on October 30, 2001 under Presidential Decree (90) Hua-Zong-Yi-Yi-Zi-9000213930; effective for a period of ten years from the date of promulgation Content Article 1 This Act is set forth for expediting the improvement of drainage and flood control functions of Keelung River so as to address the serious flooding problem along the Keelung River Basin and improve the quality of life of the local residents. Article 2 The criteria for compensating Keelung River related disasters shall observe the most favorable terms offered to victims of natural disaster. Article 3 The term “central authority” depicted herein refers to the Ministry of Economic Affairs. Article 4 The term “Keelung River and Keelung River Basin” depicted herein refer to sections and reaches within the Keelung River watershed covering the administrative regions of Taipei City, Taipei County and Keelung City. Article 5 The funds required for effectively managing the Keelung River and improving its drainage and flood control system should fall under the special budget program and be raised by issuing government bonds; the issue is not subject to the annual cap of debt financing under the Public Debt Management Act. Article 6 In order to expedite the improvement of drainage and flood control functions of Keelung River, the government may, for the purpose of bypassing restrictions provided under other laws, execute the management program in accordance with the provisions of the Temporary Act for Post-921 Quake Reconstruction. -
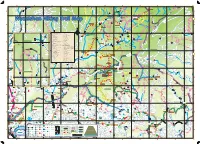
Wuzeishan Hiking Trail Map Lane 95 Bridge Connecting Point to the Small Picture on the Left
(Lane 43, Pingjing St, Industry Rd) Pinding Ancient Canal Ancient Pinding L a n S27 e Mt. Xinzhentou Dingshan 9 3 , (Xiajingque Industry Rd) Mt. Xingdui P i n g j i n Jingque Stream Jingque g Taozijiao Bridge S t ( N e Fengguizui Trail i l Mt. Neishuanxi i a Ciyun o nt C e I a (Xiaguoxi Industry Rd) Industry (Xiaguoxi Temple n ci nal d u s Stamp Pavilion An Wuzhishan Industry Rd t r Hi y g Qingfeng Pavilion n Tianweizi Bridge Wanxi Industry Rd ) d R i k d i g ng n Xiwan Rd Pi T r Pingjing St ail (Chencuo Industry Rd) S19 Neicuo Neicuo Bridge Shilin District, Taipei Sec 3, Zhishan Rd Xizhi District, New Taipei Daqitou Trail Chedengjiao Wuzeishan Hiking Trail Map Lane 95 Bridge Connecting point to the small picture on the left. Connecting point to the small picture ry Rd) Mt. Ewei ndust S I h u a St, n g g x i n g o ji Mt. Shuanxi u Mt. Wuzhishan g H i s in t P o r , i c Pingjing St (Pingxi Industry Rd) Industry (Pingxi St Pingjing Pingdeng S18 T 106 Shengren r (Lane 42, Pingjing St, Industry Rd) a Zhulin Trail Pingdingguchaun i Wanxi Industry Rd l (Lane Hiking Trail Entrance Waterfall N e Mt. Suiwei i Lane 371 s h (Lane 105, Pingjing St, Industry Rd) Industry St, Pingjing 105, (Lane u a n S Pingxi Trail t r e Mt. Meihua a Zhengtian Gongping Bridge m Temple Xiwan 3rd Bridge D6 Nature Trail Index of the Trails in Taipei S18 D7 The North Trail Shengren E5 Daluntoushan and Dalunweishan Shilin District, Taipei Xiwan Rd Yongzhen Trail Bridge Shengren Shanxi Touristic TaiPower Electricity Hiking Trail E6 Yuanming Temple Trail Bridge Farm Relay Station E5 Zhongshe Rd Branch Guandi Lutian Xinyi Rd B7 Daqitou Trail Temple Huaxin 2nd Rd E6 Bishan Rd Branch Mt. -

Response of Salt Transport and Residence Time to Geomorphologic Changes in an Estuarine System
water Article Response of Salt Transport and Residence Time to Geomorphologic Changes in an Estuarine System Wen-Cheng Liu *, Min-Hsin Ke and Hong-Ming Liu Department of Civil and Disaster Prevention Engineering, National United University, Miaoli 36063, Taiwan; [email protected] (M.-H.K.); [email protected] (H.-M.L.) * Correspondence: [email protected]; Tel.: +886-37-383357 Received: 21 March 2020; Accepted: 10 April 2020; Published: 12 April 2020 Abstract: Anthropogenic changes in tidal estuaries have significantly altered bathymetry and topography over the past half century. The geomorphic-driven changes in estuarine hydrodynamics and salt transport remain unclear. To explore this issue, a SELFE (Semi-implicit Eulaerian-Lagrangian Finite Element) -based model was developed and utilized in a case study in the Danshui River, Taiwan. The model was calibrated and validated using observed water level, current, and salinity data from 2015, 2016, and 2017. The performance of the SELFE model corresponded well to the measured data. Furthermore, the validated model was utilized to analyze the hydrodynamics, residual current, limit of salt intrusion, and residence time under the predevelopment (1981) and present (2015) conditions. The predicted results revealed that the time lag of water surface elevation at both high tide and low tide under the present condition was approximately 0.5–2 h shorter under the predevelopment condition. The residual circulation under the predevelopment condition was stronger than under the present condition for low flow, causing the limit of salt intrusion to extend further upstream under the predevelopment condition compared to the limit of salt intrusion under the present condition. -

On TAIPEI OG INS I D 2017 Vol
Centered Vol. 18 | 01 SEP on TAIPEI 2017 The Queen of Marathons Jake’s Country Kitchen Emotions The Secret to Great Coffee Kuanyin Cave A publication of the Community Services Center 2017 FALL & WINTER ACTIVITIES CATALOG INSIDE Sept cover.indd 1 2017/8/28 2:54:04 PM Sept cover.indd 2 2017/8/28 2:54:16 PM CONTENTS September 2017 volume 18 issue 1 CSC DESIGN From the Editors 5 The Golden Pin Design Award and Kiddies Korner 6 Motion Graphics Designer Keng-Ming Liu 10 Center September Gallery 7 Events about Town 8 Chinese Language Classes 9 PROFILE Book Clubs: September 9 The Queen of Marathons 12 CSC Business Classified 34 Jake’s Country Kitchen – A Long-standing Community Tradition 15 An Accidental Idea – The iceSpring Co. 23 Publisher Community Services Center, Taipei Editor Suzan Babcock SUPPLEMENT Co-editor Richard Saunders Advertising Manager Naomi Kaly 2017 Fall & Winter Activities catalog 17 [email protected] Magazine Email Tel 02-2836-8134 Fax 02-2835-2530 PHOTOGRAPHY Community Services Stéphane Corcuff & Wesley Oosthuizen 21 Center Editorial Panel Siew Kang, Fred Voigtmann Printed by Farn Mei Printing Co., Ltd. OUTLOOK 1F, No. 102, Hou Kang Street, Shilin District, Taipei Emotions – The Precious Gifts of Life 26 Tel: 02-2882-6748 Fax: 02-2882-6749 E-mail: [email protected] FOOD & DRINKS Centered on Taipei is a publication of the Community Services Center, 25, Lane 290, Zhongshan N. Rd., Sec. 6, Tianmu, Taipei, Taiwan The Secret to Great Coffee 27 Tel: 02-2836-8134 Cheogajip 30 fax: 02-2835-2530 e-mail: [email protected] Correspondence may be sent to the editor at coteditor@ FASHION & BEAUTY communitycenter.org.tw. -

2020 Fall & Winter
2020 Fall & Winter Activities Fall_Spring_2020.indd 1 2020/7/31 下午2:15 Tel: 8145-9007 Ext. 1115 E-mail: [email protected] Website: tes.tp.edu.tw Online Application: tes.openapply.com FB: Taipei European School The Taipei European School consists of 1,750 students aged 3-19 from over 55 nations, and offers curricula from the U.K., Germany and France. Classes start from nursery level and continue all the French German British Primary British Secondary way through to our fully accredited International Baccalaureate High School Programme, with our Section Section Section & High School Section graduates continuing onward to top Universities across the world! For more information, please visit our website or contact the Admissions Office. Fall_Spring_2020.indd 2 2020/7/29 下午10:16 Tel: 8145-9007 Ext. 1115 E-mail: [email protected] Website: tes.tp.edu.tw Online Application: tes.openapply.com FB: Taipei European School Welcome To The Center August 5, 2020 Registration Information Dear Friends, Advance registration is required for all Center activities. Registration may be Welcome to the Community Services Center! done by phone, email, online or in person. For online registration please go to the Center’s website: http://www.communitycenter.org.tw We have all faced a challenging year due to the COVID-19 pandemic and we hope that you and your loved ones remain healthy, safe and secure, wherever they may Payment is due at least one week prior to the start of any activity. Some be. activities may require earlier payment. Should an activity become fully subscribed and a wait list created; payment will be due upon request. -

Northeast Und Yilan North Coast and Guanyinshan Taipei
Nordtaiwan Wenn man das kulturelle Gesicht Taiwans, die einzigartige Naturkulisse und das urbane Ufer schlagen oder nehmen Sie eine Dusche im Freien, entspannen in heißen Quellen; Flair der Insel auf einen Blick erfassen möchte, dann ist man im Norden Taiwans genau genießen die Ruhe in kleinen Städte und die Nostalgie historischer Orte. Sie können Yangmingshan 北投、陽明山之溫泉與人文 richtig. Die Region umfasst die Städte und Landkreise Taipeh, New Taipei, Keelung, Taoyuan, die lokalen Spezialitäten kosten und das Kunsthandwerk der Region bewundern. Der Hsinchu und Yilan, von denen alle zu jeder Jahreszeit ihre eigenen Vorzüge haben. Der Yangmingshan-Nationalpark ist zum Beispiel ein eindrucksvolles Geothermalgebiet und Nationalpark Nationalpark Yangmingshan, das National Scenic Area Northcoast and Guanyinshan, wie liegt nur 50 Kilometer von Taipeh entfernt. Das National Scenic Area Northcoast and Guan- auch das National Scenic Area Northeastcoast verleihen dem Großraum Taipeh einen yinshan kennt man hingegen für spektakuläre Steinküsten und bizarre Felsformationen. natürlichen Rückzugsort. Schauen Sie den Wellen des Meeres zu, wie sie sanft an das die alte US-amerikanische Militärbasis in Shanzaihou. Wenn Sie die Route von Süden Yangmingshan, ursprünglich Cao Mountain genannt, ist von der Datun-Vulkangruppe antreten, sollten Sie unbedingt den sehenswerten Juansi-Wasserfall besuchen. Aus umgeben und das Ziel schlechthin, um Taiwans Vulkane zu erleben. Die kegelförmige Norden kommend gibt es u. a. die historische Mauerwerksstätte und die alte Stein- oder glockenförmige Struktur der Berge, zusammen mit Kratern, Spalten und Seen, haben brücke Xuyan zu sehen. Darüber hinaus finden sich entlang der Strecke einige Ruinen einzigartige geologische Formationen hervorgebracht. Heiße Quellen und geothermische aus der Qing-Dynastie. Aktivitäten zählen daher auch zu den Highlights im Yangmingshan-Nationalpark. -

Taipei City Cycling
Service Times of Taipei Riverside Bike Rental Centers Shuang River Service Time Danshuei River Keelung Riverside Bikeway Name & Tel. Location May – September (Summer) October - April (Winter) Keelung River Holidays Weekdays Holidays Weekday To the north of Guandu Guandu Temple and beside (02)2858-4768 Guandu Wharf Jingmei River Enter Dadaocheng Evacuation Gate at the Dadaocheng end of Minsheng W. Rd.; Xindian River (02)2557-0692 it is on the south side of Dadaocheng Wharf Upon entering the Lin-antai Evacuation Gate on the left bank of the Lin-Antai Historic Home Turn to Yingfeng Keelung River, visitors will see a sign explaining the origin and the river The southern Fujian style building adjoined the Evacuation Gate from Rainbow Bridge Xinsheng Park boasts ideal ventilation and the ability to Dajia Tayou Rd.; it is beside Rental Hours: Rental Hours: Rental Hours: Rental Hours: (02)2517-5568 remediation history of the Keelung River, enabling the public to get a better There are many sports facilities inside the ward off the chilling wind in wintertime, demonstrating the bikeway in the Dazhi 08:00-18:30 08:00-12:00 08:00-17:30 08:00-12:00 riverside park, including the red clay baseball a combination of Chinese feng-shui, as well as scientific Taipei City Bridge direction Return (Lunch break) Return (Lunch break) understanding of the place while enjoying their leisure activities. Dajia Watching the Ferris Wheel of Miramar and pragmatic functions. Deadline: 14:00-18:30 Deadline: 14:00-17:30 field, softball field, skating rink, football field, Turn to Jingye cross- 19:30 Return 18:30 Return While bicycling, why not take a break to enjoy the view of volleyball court, tennis court, etc. -

City Memories - Unforgettable Flavors Maokong Gondola Maokong Add: 35, Ln
Apr. ~ Jun., 2016 No.3 Delicacy Travel Notes Old Taipei Rambles Taipei Visitor Information Centers Taipei Main Station Add: 3, Beiping W. Rd., Taipei City (southwest area of Main Hall on 1F) Visitor Information Center Tel: (02) 2312-3256 Songshan Airport Add: 340-10, Dunhua N. Rd., Taipei City (Arrival Hall, Terminal 2) Visitor Information Center Tel: (02) 2546-4741 MRT Taipei 101 / World Trade Add: B1, 20, Sec. 5, Xinyi Rd., Taipei City (near Exit No. 5) Center Station Visitor Information Center Tel: (02) 2758-6593 MRT Ximen Station Add: B1, 32-1, Baoqing Rd., Taipei City (near Exit No. 5) Visitor Information Center Tel: (02) 2375-3096 MRT Jiantan Station Add: 65, Sec. 5, Zhongshan N. Rd., Taipei City (near Exit No. 1) Visitor Information Center Tel: (02) 2883-0313 MRT Beitou Station Add: 1, Guangming Rd., Taipei City (left side of station entrance) Visitor Information Center Tel: (02) 2894-6923 Miramar Entertainment Add: 20, Jingye 3rd Rd., Taipei City (in rear of fountain plaza, 1F) Park Visitor Center Tel: (02) 8501-2762 Add: 6, Zhongshan Rd., Taipei City (near the Beitou Garden Spa) Plum Garden Visitor Center Tel: (02) 2897-2647 City Memories - Unforgettable Flavors Maokong Gondola Maokong Add: 35, Ln. 38, Sec. 3, Zhinan Rd., Taipei City (near exit of Maokong Station) Station Visitor Center Tel: (02) 2937-8563 In this early summer, "Fun Taipei" is sporting all-new attire with more diversified units and a Add: 44, Sec. 1, Dihua St., Taipei City (inside URS44 Dadaocheng Story House) Dadaocheng Visitor Center different layout and style, plus more practical and plentiful travel and living information. -

Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis
Int. J. Environ. Res. Public Health 2012, 9, 3085-3100; doi:10.3390/ijerph9093085 OPEN ACCESS International Journal of Environmental Research and Public Health ISSN 1660-4601 www.mdpi.com/journal/ijerph Article Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis Yen-Chang Chen 1, Hui-Chung Yeh 2 and Chiang Wei 3,* 1 Department of Civil Engineering, National Taipei University of Technology, Taipei 10608, Taiwan; E-Mail: [email protected] 2 Department of Natural Resources, Chinese Culture University, Taipei 11114, Taiwan; E-Mail: [email protected] 3 Experimental Forest, National Taiwan University, Jhu-Shan, Nantou 55750, Taiwan * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +886-49-265-8412; Fax: +886-49-263-1943. Received: 20 June 2012; in revised form: 16 August 2012 / Accepted: 21 August 2012 / Published: 29 August 2012 Abstract: Tidal streams are complex watercourses that represent a transitional zone between riverine and marine systems; they occur where fresh and marine waters converge. Because tidal circulation processes cause substantial turbulence in these highly dynamic zones, tidal streams are the most productive of water bodies. Their rich biological diversity, combined with the convenience of land and water transports, provide sites for concentrated populations that evolve into large cities. Domestic wastewater is generally discharged directly into tidal streams in Taiwan, necessitating regular evaluation of the water quality of these streams. Given the complex flow dynamics of tidal streams, only a few models can effectively evaluate and identify pollution levels. This study evaluates the river pollution index (RPI) in tidal streams by using kriging analysis. -

Golden Jin-Zi-Bei Trail Information Center Houtong Train Mountain City Station Jieshou Bridge Full of Memories Mt
New Taipei City Special Scenic Area | Ruifang To Shuangxi Fuxing Bridge Coal-transporting Bridge Shuangxi Coal-dressing Plant Vision Hall Golden Jin-Zi-Bei Trail Information Center Houtong Train Mountain City Station Jieshou Bridge full of Memories Mt. Wuerchahu Dacu Pit Old street . Sunset . Old Flavor Wengzaitan Bridge Golden Temple Jinguashi is a mountain town full of memories Houtong and a legendary golden town. Thanks to a movie Visitor Center depicting this place, this golden mountain town is New Houtong North- no longer just an ancient memory. Come through Elementary School Link the tunnel and visit this golden town with the Railway Golden Ecological Park and Jiufen old streets and Keelung River Houtong. Crown Prince Chalet Jiufen Jiufen old streets Gold Ecological Jinshi Park Sanye Bangkong Qingbian Shengping Theater Qingbian Shuqi Quanji Guashan Jiufen Visitor Yuanshanzi Taiwan P.O.W Center To Keelung Memorial Park Guashan Jiufen Mt. Keelung and Ruiba Highway Guantaoping Jinshui Qingyun Ruifang District office Ruifang Train Station Shuinadong To Wanli Thirteen-tiered Relics Art Gallery Wanrui Expressway To Keelung Advertisement Printed by Tourism and Travel Department, New Taipei City Government http://tour.ntpc.gov.tw Updated in June 2013 Route Suggestions Jiufen old streets 1-day trip Houtong Taipei → Jiufen old street → Jiufen delicacies → Mt.Keelung → Taipei 11 Coal-transporting Bridge Jinguashi Golden Mountain Town 1-day trip Houtong Coal-Mine Ecological Park Taipei → Gold Ecological Park → Environmental Museum → Benshan Fifth Pit → Ruisan's coal- Golden Temple → International Final Battle Peace Memorial Park → Golden waterfall → Houtong is a small station on Pingxi Route Railway. Due to its rich coal output, transporting bridge Shueinandong → Taipei this place became a small town, and today it has become the Houtong Coal has a unique and Jinguashi, Jinfen 2-day trip Ecological Park that features the coal mining culture, thanks to its history and classic appearance. -

Chapter 10 Public Infrastructure
Chapter 10 Public Infrastructure Public infrastructure is a crucial aspect of the quality of life of Taipei City’s residents. 2007 witnessed the completion of the Fubei Underpass and Kanghu Road; residents of Taipei City now enjoy improved traffic service. 75.93% of the sidewalks in Taipei City have been renovated to improve pedestrian walkways. Flood control and wastewater sewage reinforcements effectively protect citizens from flooding-related mishaps, and provide quality river watershed areas plus water-friendly environments. Visitors to numerous flower festivals have grown to 1.4 million, with such events serving as great venues for leisure and relaxation. Utility construction and public housing services have been renewed to benefit residents. The Taipei City Government is poised to create a resident-friendly, safe, convenient, and quality urban community by building a sound public infrastructure for its residents in limited space. 英文年鑑內頁6-10.indd 147 2008/7/1 12:46:42 PM 148 Public infrastructure is an index with which one measures social progress and residential living quality; it affects multiple aspects of people’s lives, and its influence extends far and wide; sometimes it acts as a catalyst for urban reforms. A prosperous society in turn encourages a wide array of urban construction, while a comprehensive public infrastructure project promotes metropolitan affluence. Time is needed in building a great city, and Taipei City bears witness to its historic evolution. Taipei is the nation’s capital, and the Taipei City Government actively promotes the renovation and construction of traffic sites and services, flood control, river dredging, utility construction and city rezoning projects on its solid, existing foundation, and effectively improves the quality of public infrastructure to enable citizens to enjoy a safe and cozy living environment.