DOCSLIB.ORG

7: Fourier Transforms: Convolution and Parseval's Theorem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
7: Fourier Transforms: Convolution and Parseval's Theorem 7: Fourier Transforms: Convolution and Parseval’s Theorem • Multiplication of Signals • Multiplication Example • Convolution Theorem • Convolution Example • Convolution Properties • Parseval’s Theorem • Energy Conservation • Energy Spectrum 7: Fourier Transforms: • Summary Convolution and Parseval's Theorem E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 1 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem • Multiplication of Signals • Multiplication Example • Convolution Theorem • Convolution Example • Convolution Properties • Parseval’s Theorem • Energy Conservation • Energy Spectrum • Summary E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem • Convolution Example R R • Convolution Properties • Parseval’s Theorem • Energy Conservation • Energy Spectrum • Summary E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem • Energy Conservation • Energy Spectrum • Summary E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary R R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e R R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh R R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df R R R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df +∞ i2πft = Rf=−∞ RW (f)e df R R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df +∞ i2πft = Rf=−∞ RW (f)e df R +∞ where W (fR) = h=−∞ U(h)V (f − h)dh R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df +∞ i2πft = Rf=−∞ RW (f)e df R +∞ where , W (fR) = h=−∞ U(h)V (f − h)dh U(f) ∗ V (f) R E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df +∞ i2πft = Rf=−∞ RW (f)e df R +∞ where , W (fR) = h=−∞ U(h)V (f − h)dh U(f) ∗ V (f) This is the convolutionR of the two spectra U(f) and V (f). E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 Multiplication of Signals 7: Fourier Transforms: Convolution and Parseval’s Question: What is the Fourier transform of w(t) = u(t)v(t) ? Theorem +∞ i2πht +∞ i2πgt • Multiplication of Signals Let u(t) = U(h)e dh and v(t) = V (g)e dg • Multiplication Example h=−∞ g=−∞ • Convolution Theorem [Note use of different dummy variables] • Convolution Example R R • Convolution Properties w(t) = u(t)v(t) • Parseval’s Theorem +∞ +∞ • Energy Conservation = U(h)ei2πhtdh V (g)ei2πgtdg • Energy Spectrum h=−∞ g=−∞ • Summary +∞ +∞ i2π(h+g)t [merge (··· )] = Rh=−∞ U(h) g=−∞ VR(g)e dg dh e Now we makeR a change ofR variable in the second integral: g = f − h +∞ +∞ i2πft = h=−∞ U(h) f=−∞ V (f − h)e df dh ∞ +∞ i2πft [swap ] = Rf=−∞ h=−∞R U(h)V (f − h)e dh df +∞ i2πft = Rf=−∞ RW (f)e df R +∞ where , W (fR) = h=−∞ U(h)V (f − h)dh U(f) ∗ V (f) This is the convolutionR of the two spectra U(f) and V (f). w(t) = u(t)v(t) ⇔ W (f) = U(f) ∗ V (f) E1.10FourierSeriesandTransforms(2014-5559) FourierTransform - Parseval and Convolution: 7 – 2 / 10 < < Multiplication Example 7: Fourier Transforms:
Load more

Recommended publications
  • Convolution! (CDT-14) Luciano Da Fontoura Costa
    Convolution! (CDT-14) Luciano da Fontoura Costa To cite this version: Luciano da Fontoura Costa. Convolution! (CDT-14). 2019. hal-02334910 HAL Id: hal-02334910 https://hal.archives-ouvertes.fr/hal-02334910 Preprint submitted on 27 Oct 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Convolution! (CDT-14) Luciano da Fontoura Costa [email protected] S~aoCarlos Institute of Physics { DFCM/USP October 22, 2019 Abstract The convolution between two functions, yielding a third function, is a particularly important concept in several areas including physics, engineering, statistics, and mathematics, to name but a few. Yet, it is not often so easy to be conceptually understood, as a consequence of its seemingly intricate definition. In this text, we develop a conceptual framework aimed at hopefully providing a more complete and integrated conceptual understanding of this important operation. In particular, we adopt an alternative graphical interpretation in the time domain, allowing the shift implied in the convolution to proceed over free variable instead of the additive inverse of this variable. In addition, we discuss two possible conceptual interpretations of the convolution of two functions as: (i) the `blending' of these functions, and (ii) as a quantification of `matching' between those functions.
    [Show full text]
  • The Convolution Theorem
    Module 2 : Signals in Frequency Domain Lecture 18 : The Convolution Theorem Objectives In this lecture you will learn the following We shall prove the most important theorem regarding the Fourier Transform- the Convolution Theorem We are going to learn about filters. Proof of 'the Convolution theorem for the Fourier Transform'. The Dual version of the Convolution Theorem Parseval's theorem The Convolution Theorem We shall in this lecture prove the most important theorem regarding the Fourier Transform- the Convolution Theorem. It is this theorem that links the Fourier Transform to LSI systems, and opens up a wide range of applications for the Fourier Transform. We shall inspire its importance with an application example. Modulation Modulation refers to the process of embedding an information-bearing signal into a second carrier signal. Extracting the information- bearing signal is called demodulation. Modulation allows us to transmit information signals efficiently. It also makes possible the simultaneous transmission of more than one signal with overlapping spectra over the same channel. That is why we can have so many channels being broadcast on radio at the same time which would have been impossible without modulation There are several ways in which modulation is done. One technique is amplitude modulation or AM in which the information signal is used to modulate the amplitude of the carrier signal. Another important technique is frequency modulation or FM, in which the information signal is used to vary the frequency of the carrier signal. Let us consider a very simple example of AM. Consider the signal x(t) which has the spectrum X(f) as shown : Why such a spectrum ? Because it's the simplest possible multi-valued function.
    [Show full text]
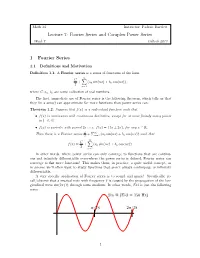
  • Lecture 7: Fourier Series and Complex Power Series 1 Fourier
    Math 1d Instructor: Padraic Bartlett Lecture 7: Fourier Series and Complex Power Series Week 7 Caltech 2013 1 Fourier Series 1.1 Definitions and Motivation Definition 1.1. A Fourier series is a series of functions of the form 1 C X + (a sin(nx) + b cos(nx)) ; 2 n n n=1 where C; an; bn are some collection of real numbers. The first, immediate use of Fourier series is the following theorem, which tells us that they (in a sense) can approximate far more functions than power series can: Theorem 1.2. Suppose that f(x) is a real-valued function such that • f(x) is continuous with continuous derivative, except for at most finitely many points in [−π; π]. • f(x) is periodic with period 2π: i.e. f(x) = f(x ± 2π), for any x 2 R. C P1 Then there is a Fourier series 2 + n=1 (an sin(nx) + bn cos(nx)) such that 1 C X f(x) = + (a sin(nx) + b cos(nx)) : 2 n n n=1 In other words, where power series can only converge to functions that are continu- ous and infinitely differentiable everywhere the power series is defined, Fourier series can converge to far more functions! This makes them, in practice, a quite useful concept, as in science we'll often want to study functions that aren't always continuous, or infinitely differentiable. A very specific application of Fourier series is to sound and music! Specifically, re- call/observe that a musical note with frequency f is caused by the propogation of the lon- gitudinal wave sin(2πft) through some medium.
    [Show full text]
  • Fourier Series
    Academic Press Encyclopedia of Physical Science and Technology Fourier Series James S. Walker Department of Mathematics University of Wisconsin–Eau Claire Eau Claire, WI 54702–4004 Phone: 715–836–3301 Fax: 715–836–2924 e-mail: [email protected] 1 2 Encyclopedia of Physical Science and Technology I. Introduction II. Historical background III. Definition of Fourier series IV. Convergence of Fourier series V. Convergence in norm VI. Summability of Fourier series VII. Generalized Fourier series VIII. Discrete Fourier series IX. Conclusion GLOSSARY ¢¤£¦¥¨§ Bounded variation: A function has bounded variation on a closed interval ¡ ¢ if there exists a positive constant © such that, for all finite sets of points "! "! $#&% (' #*) © ¥ , the inequality is satisfied. Jordan proved that a function has bounded variation if and only if it can be expressed as the difference of two non-decreasing functions. Countably infinite set: A set is countably infinite if it can be put into one-to-one £0/"£ correspondence with the set of natural numbers ( +,£¦-.£ ). Examples: The integers and the rational numbers are countably infinite sets. "! "!;: # # 123547698 Continuous function: If , then the function is continuous at the point : . Such a point is called a continuity point for . A function which is continuous at all points is simply referred to as continuous. Lebesgue measure zero: A set < of real numbers is said to have Lebesgue measure ! $#¨CED B ¢ £¦¥ zero if, for each =?>A@ , there exists a collection of open intervals such ! ! D D J# K% $#L) ¢ £¦¥ ¥ ¢ = that <GFIH and . Examples: All finite sets, and all countably infinite sets, have Lebesgue measure zero. "! "! % # % # Odd and even functions: A function is odd if for all in its "! "! % # # domain.
    [Show full text]
  • FOURIER TRANSFORM Very Broadly Speaking, the Fourier Transform Is a Systematic Way to Decompose “Generic” Functions Into
    FOURIER TRANSFORM TERENCE TAO Very broadly speaking, the Fourier transform is a systematic way to decompose “generic” functions into a superposition of “symmetric” functions. These symmetric functions are usually quite explicit (such as a trigonometric function sin(nx) or cos(nx)), and are often associated with physical concepts such as frequency or energy. What “symmetric” means here will be left vague, but it will usually be associated with some sort of group G, which is usually (though not always) abelian. Indeed, the Fourier transform is a fundamental tool in the study of groups (and more precisely in the representation theory of groups, which roughly speaking describes how a group can define a notion of symmetry). The Fourier transform is also related to topics in linear algebra, such as the representation of a vector as linear combinations of an orthonormal basis, or as linear combinations of eigenvectors of a matrix (or a linear operator). To give a very simple prototype of the Fourier transform, consider a real-valued function f : R → R. Recall that such a function f(x) is even if f(−x) = f(x) for all x ∈ R, and is odd if f(−x) = −f(x) for all x ∈ R. A typical function f, such as f(x) = x3 + 3x2 + 3x + 1, will be neither even nor odd. However, one can always write f as the superposition f = fe + fo of an even function fe and an odd function fo by the formulae f(x) + f(−x) f(x) − f(−x) f (x) := ; f (x) := . e 2 o 2 3 2 2 3 For instance, if f(x) = x + 3x + 3x + 1, then fe(x) = 3x + 1 and fo(x) = x + 3x.
    [Show full text]
  • The Summation of Power Series and Fourier Series
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Journal of Computational and Applied Mathematics 12&13 (1985) 447-457 447 North-Holland The summation of power series and Fourier . series I.M. LONGMAN Department of Geophysics and Planetary Sciences, Tel Aviv University, Ramat Aviv, Israel Received 27 July 1984 Abstract: The well-known correspondence of a power series with a certain Stieltjes integral is exploited for summation of the series by numerical integration. The emphasis in this paper is thus on actual summation of series. rather than mere acceleration of convergence. It is assumed that the coefficients of the series are given analytically, and then the numerator of the integrand is determined by the aid of the inverse of the two-sided Laplace transform, while the denominator is standard (and known) for all power series. Since Fourier series can be expressed in terms of power series, the method is applicable also to them. The treatment is extended to divergent series, and a fair number of numerical examples are given, in order to illustrate various techniques for the numerical evaluation of the resulting integrals. Keywork Summation of series. 1. Introduction We start by considering a power series, which it is convenient to write in the form s(x)=/.Q-~2x+&x2..., (1) for reasons which will become apparent presently. Here there is no intention to limit ourselves to alternating series since, even if the pLkare all of one sign, x may take negative and even complex values. It will be assumed in this paper that the pLk are real.
    [Show full text]
  • An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms
    An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms Notes prepared for MA3139 Arthur L. Schoenstadt Department of Applied Mathematics Naval Postgraduate School Code MA/Zh Monterey, California 93943 August 18, 2005 c 1992 - Professor Arthur L. Schoenstadt 1 Contents 1 Infinite Sequences, Infinite Series and Improper Integrals 1 1.1Introduction.................................... 1 1.2FunctionsandSequences............................. 2 1.3Limits....................................... 5 1.4TheOrderNotation................................ 8 1.5 Infinite Series . ................................ 11 1.6ConvergenceTests................................ 13 1.7ErrorEstimates.................................. 15 1.8SequencesofFunctions.............................. 18 2 Fourier Series 25 2.1Introduction.................................... 25 2.2DerivationoftheFourierSeriesCoefficients.................. 26 2.3OddandEvenFunctions............................. 35 2.4ConvergencePropertiesofFourierSeries.................... 40 2.5InterpretationoftheFourierCoefficients.................... 48 2.6TheComplexFormoftheFourierSeries.................... 53 2.7FourierSeriesandOrdinaryDifferentialEquations............... 56 2.8FourierSeriesandDigitalDataTransmission.................. 60 3 The One-Dimensional Wave Equation 70 3.1Introduction.................................... 70 3.2TheOne-DimensionalWaveEquation...................... 70 3.3 Boundary Conditions ............................... 76 3.4InitialConditions................................
    [Show full text]
  • The Discrete-Time Fourier Transform and Convolution Theorems: a Brief Tutorial
    The Discrete-Time Fourier Transform and Convolution Theorems: A Brief Tutorial Yi-Wen Liu 25 Feb 2013 (Revised 21 Sep 2015) 1 Definitions and interpretation 1.1 Units Throughout this semester, we will use the integer-valued variable n as the time variable for discrete-time signal processing; that is, n = −∞, ..., −1, 0, 1, ..., ∞. In this convention, the unit of n is dimensionless, but be aware that in reality the sampling period is 1/fs, where fs denotes the sampling rate. In some text books, 1/fs is denoted as T , and its unit is second. In this course we do not do this, thereby favoring conciseness of notations. 1.2 Definition of DTFT The discrete-time Fourier transform (DTFT) of a discrete-time signal x[n] is a function of frequency ω defined as follows: ∞ ∆ X(ω) = x[n]e−jωn. (1) n=−∞ X Conceptually, the DTFT allows us to check how much of a tonal component at fre- quency ω is in x[n]. The DTFT of a signal is often also called a spectrum. Note that X(ω) is complex-valued. So, the absolute value |X(ω)| represents the tonal component’s magnitude, and the angle ∠X(ω) tells us the phase of the tonal component. Also note that Eq. (1) defines the DTFT as the inner product between the signal and the complex exponential tone e−jωn. Because complex exponentials {e−jωn,ω ∈ [−π, π]} form a complete family of orthogonal bases for (practically) all signals of interest, what Eq. (1) essentially does is to project x[n] onto the space spanned by all complex exponen- tials.
    [Show full text]
  • Harmonic Analysis from Fourier to Wavelets
    STUDENT MATHEMATICAL LIBRARY ⍀ IAS/PARK CITY MATHEMATICAL SUBSERIES Volume 63 Harmonic Analysis From Fourier to Wavelets María Cristina Pereyra Lesley A. Ward American Mathematical Society Institute for Advanced Study Harmonic Analysis From Fourier to Wavelets STUDENT MATHEMATICAL LIBRARY IAS/PARK CITY MATHEMATICAL SUBSERIES Volume 63 Harmonic Analysis From Fourier to Wavelets María Cristina Pereyra Lesley A. Ward American Mathematical Society, Providence, Rhode Island Institute for Advanced Study, Princeton, New Jersey Editorial Board of the Student Mathematical Library Gerald B. Folland Brad G. Osgood (Chair) Robin Forman John Stillwell Series Editor for the Park City Mathematics Institute John Polking 2010 Mathematics Subject Classification. Primary 42–01; Secondary 42–02, 42Axx, 42B25, 42C40. The anteater on the dedication page is by Miguel. The dragon at the back of the book is by Alexander. For additional information and updates on this book, visit www.ams.org/bookpages/stml-63 Library of Congress Cataloging-in-Publication Data Pereyra, Mar´ıa Cristina. Harmonic analysis : from Fourier to wavelets / Mar´ıa Cristina Pereyra, Lesley A. Ward. p. cm. — (Student mathematical library ; 63. IAS/Park City mathematical subseries) Includes bibliographical references and indexes. ISBN 978-0-8218-7566-7 (alk. paper) 1. Harmonic analysis—Textbooks. I. Ward, Lesley A., 1963– II. Title. QA403.P44 2012 515.2433—dc23 2012001283 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given.
    [Show full text]
  • Fourier Transforms & the Convolution Theorem
    Convolution, Correlation, & Fourier Transforms James R. Graham 11/25/2009 Introduction • A large class of signal processing techniques fall under the category of Fourier transform methods – These methods fall into two broad categories • Efficient method for accomplishing common data manipulations • Problems related to the Fourier transform or the power spectrum Time & Frequency Domains • A physical process can be described in two ways – In the time domain, by h as a function of time t, that is h(t), -∞ < t < ∞ – In the frequency domain, by H that gives its amplitude and phase as a function of frequency f, that is H(f), with -∞ < f < ∞ • In general h and H are complex numbers • It is useful to think of h(t) and H(f) as two different representations of the same function – One goes back and forth between these two representations by Fourier transforms Fourier Transforms ∞ H( f )= ∫ h(t)e−2πift dt −∞ ∞ h(t)= ∫ H ( f )e2πift df −∞ • If t is measured in seconds, then f is in cycles per second or Hz • Other units – E.g, if h=h(x) and x is in meters, then H is a function of spatial frequency measured in cycles per meter Fourier Transforms • The Fourier transform is a linear operator – The transform of the sum of two functions is the sum of the transforms h12 = h1 + h2 ∞ H ( f ) h e−2πift dt 12 = ∫ 12 −∞ ∞ ∞ ∞ h h e−2πift dt h e−2πift dt h e−2πift dt = ∫ ( 1 + 2 ) = ∫ 1 + ∫ 2 −∞ −∞ −∞ = H1 + H 2 Fourier Transforms • h(t) may have some special properties – Real, imaginary – Even: h(t) = h(-t) – Odd: h(t) = -h(-t) • In the frequency domain these
    [Show full text]
  • Fourier Analysis
    Chapter 1 Fourier analysis In this chapter we review some basic results from signal analysis and processing. We shall not go into detail and assume the reader has some basic background in signal analysis and processing. As basis for signal analysis, we use the Fourier transform. We start with the continuous Fourier transformation. But in applications on the computer we deal with a discrete Fourier transformation, which introduces the special effect known as aliasing. We use the Fourier transformation for processes such as convolution, correlation and filtering. Some special attention is given to deconvolution, the inverse process of convolution, since it is needed in later chapters of these lecture notes. 1.1 Continuous Fourier Transform. The Fourier transformation is a special case of an integral transformation: the transforma- tion decomposes the signal in weigthed basis functions. In our case these basis functions are the cosine and sine (remember exp(iφ) = cos(φ) + i sin(φ)). The result will be the weight functions of each basis function. When we have a function which is a function of the independent variable t, then we can transform this independent variable to the independent variable frequency f via: +1 A(f) = a(t) exp( 2πift)dt (1.1) −∞ − Z In order to go back to the independent variable t, we define the inverse transform as: +1 a(t) = A(f) exp(2πift)df (1.2) Z−∞ Notice that for the function in the time domain, we use lower-case letters, while for the frequency-domain expression the corresponding uppercase letters are used. A(f) is called the spectrum of a(t).
    [Show full text]
  • STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS and INTERPRETATIONS by DSG Pollock
    STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS AND INTERPRETATIONS by D.S.G. Pollock (University of Leicester) Email: stephen [email protected] This paper expounds some of the results of Fourier theory that are es- sential to the statistical analysis of time series. It employs the algebra of circulant matrices to expose the structure of the discrete Fourier transform and to elucidate the filtering operations that may be applied to finite data sequences. An ideal filter with a gain of unity throughout the pass band and a gain of zero throughout the stop band is commonly regarded as incapable of being realised in finite samples. It is shown here that, to the contrary, such a filter can be realised both in the time domain and in the frequency domain. The algebra of circulant matrices is also helpful in revealing the nature of statistical processes that are band limited in the frequency domain. In order to apply the conventional techniques of autoregressive moving-average modelling, the data generated by such processes must be subjected to anti- aliasing filtering and sub sampling. These techniques are also described. It is argued that band-limited processes are more prevalent in statis- tical and econometric time series than is commonly recognised. 1 D.S.G. POLLOCK: Statistical Fourier Analysis 1. Introduction Statistical Fourier analysis is an important part of modern time-series analysis, yet it frequently poses an impediment that prevents a full understanding of temporal stochastic processes and of the manipulations to which their data are amenable. This paper provides a survey of the theory that is not overburdened by inessential complications, and it addresses some enduring misapprehensions.
    [Show full text]