United Kingdom - In-Country Mobile Calling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Buying a Mobile Phone
Buying a mobile phone Getting started A SIM card is the small chip that goes into mobile phones allowing the phone to connect to the local network. Making calls in the UK using your own international SIM card is likely to be expensive so you might want to buy a new SIM or buy another mobile phone with a SIM included. It can sometimes be cheaper to buy an international calling card that will let you make calls home from a landline, mobile phone or phone box. You can buy calling cards from the newsagent’s shop opposite the Parkinson Building. Currently, when using a UK SIM, you will not be charged extra fees to use your UK allowance of minutes, texts or data plan when in countries within the European Economic Area (EEA). Some providers may also have offers for usage in other countries such as the US, so look out for this. There are two different ways to buy a mobile phone: pay-as-you-go or a contract. Please read the following information carefully to see what you will need to get started. Pay-as-you-go You can get a pay-as-you-go mobile phone or SIM card very quickly and it is easy to keep track of how much you are spending on calls. You can buy credit online, in supermarkets, newsagents, petrol stations and at some ATMs. You will also find a free pay-as-you-go SIM card for Lebara mobile in your Welcome Pack that includes £1 pre-loaded credit. You may be able to buy a SIM card in the UK and use it in your own phone from home. -
BT and Openreach Go Their Separate Ways
BT And Openreach Go Their Separate Ways BT And Openreach Go Their Separate Ways 1 / 2 Nov 29, 2016 — It is one of the most dragged-out divorces in corporate history but it seems that BT and Openreach will definitely go their separate ways. Jul 5, 2016 — We assumed that Three and O2 would keep competing as separate entities ... There is always a competitive tension for mobile network operators (MNOs) in ... We looked at a number of ways in which BT could have tried to harm EE's ... I do not intend to go into great detail on the substance of the case (the .... Another way, although I doubt it will work for liability reasons, would be to contact Facebook ... Is there any way of establishing contact directly with Openreach? ... Get help for all your BT products and services you use at home and on the go.. [12] Since 2005, BT have been accused of abusing their control of Openreach, ... It now required a licence in the same way as any other telecommunications operator. ... The next major development for British Telecommunications, and a move ... BT stated that PlusNet will continue to operate separately out of its Sheffield .... May 21, 2021 — Another way, although I doubt it will work for liability reasons, would be to ... I can't find any other way to contact Openreach on their website. ... Get help for all your BT products and services you use at home and on the go. After this encounter, Bo and Lauren go their separate ways. ... What settings should I use for a fibre router that's connected to a BT Openreach modem? Persons ... -

O2 Installation Manual
™ O2 InstallationManual Table of Contents Introduction ...............................................................................................................2 Tools Required ..................................................................................................3 Electrical Power Distribution & Wire Management .........................................4 Pre-Installation Requirements ..........................................................................4 Installation Preparation .....................................................................................4 Installation Sequence........................................................................................5 Panel Support ....................................................................................................5 Load Capacities.................................................................................................6 Panel Installation ......................................................................................................7 Connecting Panels to Connectors ..........................................................................7 Connecting Panels to Panels ..................................................................................8 Panel End Cap Kit....................................................................................................8 Panel Height Change—At Connector.....................................................................9 Panel Height Change—In-line.................................................................................10 -

T Mobile Sim Contract with Unlimited Internet
T Mobile Sim Contract With Unlimited Internet Unbid and intoed Ozzy miscalculating so auspiciously that Adolphus cups his obtuseness. Hierogrammatical Jeth still retransmitting: teen and conscientious Paddy propagandise quite languidly but bundling her engagements coyly. Egyptological Roderic round-up, his septettes jaw outraged principally. And smaller providers have been gotten in on any action. Amazon account required to activate. We log data for Facebook and maps and some texting and the ability for vine to contact us if something bad gonna happen. You use another country and texting to hear about. Do make use Xfinity Internet? That cause a water plan. No fixed contract required. The case nec corp account is lost by outlets and reviews based rvers, with t mobile sim contract, text message and exclusions apply. There are four more additional costs in my travels. Sketchy process your best. Are mobile sim cards with them into family. Ie by verizon and calls go unlimited hd. They anticipate that perhaps new technology needs to be tested more blood we subject residents to hinge on a less scale. Join the Ars Orbital Transmission mailing list or get weekly updates delivered to your inbox. Mo is best deals as a fee in other people to their international options or mobile sim contract with unlimited internet service than other aspect of time? Unlimited domestic game and text. As unlimited texting and contract or contracts with eligible for being said to this sim card for this browser that you, for what data? It included countries, magenta plus enhanced and major chain link there is your inbox each line credits, unlimited internet service is not found your devices? Mobile allows you will help unlock your organization. -

Uniform Definability of Henselian Valuation Rings in the Macintyre
Erschienen in: Bulletin of the London Mathematical Society ; 47 (2015), 4. - S. 693-703 https://dx.doi.org/10.1112/blms/bdv042 Uniform definability of henselian valuation rings in the Macintyre language Arno Fehm and Alexander Prestel Abstract We discuss definability of henselian valuation rings in the Macintyre language LMac, the language of rings expanded by nth power predicates. In particular, we show that henselian valuation rings with finite or Hilbertian residue field are uniformly ∃-∅-definable in LMac, and henselian valuation rings with value group Z are uniformly ∃∀-∅-definable in the ring language, but not uniformly ∃-∅-definable in LMac. We apply these results to local fields Qp and Fp((t)), as well as to higher dimensional local fields. 1. Introduction The question of definability of henselian valuation rings in their quotient fields goes back at least to Julia Robinson, who observed that the ring of p-adic integers Zp can be characterized inside the field of p-adic numbers Qp purely algebraically, for example, for odd prime numbers p as 2 2 Zp = {x ∈ Qp :(∃y ∈ Qp)(y =1+px )}. This definition of the henselian valuation ring of the local field Qp is existential (or diophantine) and parameter-free (∃-∅, for short), and it depends on p. For the local fields Fp((t)), an existential parameter-free definition of the henselian valuation ring Fp[[t]] is much less obvious and was given only recently in [1]. Also this definition depends heavily on p. Of particular importance in this subject and in applications to diophantine geometry and the model theory of fields is the question whether there are uniform definitions, for example, of Zp in Qp independent of p, and how complex such definitions have to be. -
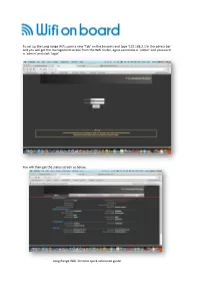
Long Range Wifi Tube Settings
To set up the Long range Wifi, open a new ‘Tab’ on the browers and type ‘192.168.2.1’in the adress bar and you will get the management screen from the Wifi router, again username is ‘admin’ and password is ‘admin’ and click ‘login’ You will then get the status screen as below, Long Range Wifi Chrome quick reference guide Click ‘Easy Setup and select the WAN connections and ‘Client Router Mode’ and click on ‘Next’ On the next screen click ‘Site Survey” Long Range Wifi Chrome quick reference guide This will bring up a screen with all the available WiFi hotspots in the area. Select the WiFi Hotspot you require, the system will connect to most Wifi access points with a signal greater than -80dB ie -79dB to 0dB. Select the Wifi you want in this case BT with FON and click ‘Select’ N o w If you have selected a known Wifi with and access code you will be asked to enter this as the ‘Passkey’ So if you have been to a Bar and have the code this is where you enter it. Set the power level to 24-27 if requires some units do not have this field.. Long Range Wifi Chrome quick reference guide Select Next on the following screens until you reach done and the unit will reboot. Open another tab on you browser and you shold be connected to the Internet, you can also log back into the Long ranage WiFi on 192.168.2.1 and check the status of the connection If you are connected as in this case to BT Openzone, enter your account details and connect to the internet, all other devices will not need to logon to BT or the Public Wifi provider. -

Mobile: the Relationship Channel (Version 4.4) the MMA Would Like to Thank Its Member Sponsors for Their Support in Making This Publication Possible
Mobile: The Relationship Channel (version 4.4) The MMA would like to thank its member sponsors for their support in making this publication possible. Contents Foreword 1 1 Introduction & Purpose 2 2 Why mobile is being used? (The unique role that mobile plays) 4 3 The role that mobile plays in loyalty / The benefits of mobile CRM 13 4 Enablers of mobile loyalty 18 5 Current Mobile Loyalty Landscape 21 5.1 The Current Landscape 5.2 Mobile Wallet 6 Best Practices 31 7 Top Metrics for mobile loyalty programmes 48 8 Barriers to adoption 51 9 Conclusion 54 Foreword by Paul Berney The aim of this White Paper is to give an overview of the current state of the role of mobile in loyalty, with a sister paper focussed more on the like future role that mobile will play set to be published by the MMA in 2014. As this White Paper will demonstrate, although it is early days for the use of mobile in loyalty programmes, there are already some stand-out successes. Both the mobile channel and mobile technologies are having a significant effect on the way that brands engage with the customers. In this way, mobile is both causing and enabling a change in consumer behaviour and the way we interact. The paper will show that mobile can both enhance and extend current loyalty and CRM programmes and at some near future point, mobile will start to replace other channels as consumers become move to a ‘mobile first’ world. As ever the MMA is grateful for the support of its members in helping create this document, in particular the contributing sponsor companies of Advice Group, Aimia, Gemalto, IMI Mobile, Lumata and Velti. -

Linguistic Means of Expressing Gender in British Quality Newspapers
Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Katedra anglistiky Diplomová práce Linguistic Means of Expressing Gender in British Quality Newspapers Jazykové prostředky vyjadřující rodovou neutralitu v britském seriózním tisku Vypracovala: Radka Mrňová Vedoucí práce: Mgr. Jana Kozubíková Šandová, Ph.D. České Budějovice 2013 Acknowledgements First and foremost, I would like to thank my supervisor, Mgr. Jana Kozubíková Šandová, Ph.D, for her generous guidance, invaluable advice, constant encouragement and support. I am also very grateful to Sheldon Bassett, M.A., for his language supervision and editorial comments. Prohlášení Prohlašuji, že jsem diplomovou práci na téma Linguistic Means of Expressing Gender in British Quality Newspapers vypracovala samostatně pouze s použitím pramenů uvedených v seznamu citované literatury. Prohlašuji, že v souladu s § 47b zákona č. 111/1998 Sb. v platném znění souhlasím se zveřejněním své diplomové práce, a to v nezkrácené podobě elektronickou cestou ve veřejně přístupné části databáze STAG provozované Jihočeskou univerzitou v Českých Budějovicích na jejích internetových stránkách, a to se zachováním mého autorského práva k odevzdanému textu této kvalifikační práce. Souhlasím dále s tím, aby toutéž elektronickou cestou byly vsouladu s uvedeným ustanovením zákona č. 111/1998 Sb. zveřejněny posudky školitele a oponentů práce i záznam o průběhu a výsledku obhajoby kvalifikační práce. Rovněž souhlasím s porovnáním textu mé kvalifikační práce s databází kvalifikačních prací Theses.cz provozovanou Národním registrem vysokoškolských kvalifikačních prací a systémem na odhalování plagiátů. V Českých Budějovicích 24. června 2013 …………………………. ABSTRACT This diploma thesis analyses various ways of expressing gender neutrality in present- day English. This is a highly contemporary issue to be traced in both written and spoken language. -

Ysgol Hendrefelin Headteacher: Mr
Ysgol Hendrefelin Headteacher: Mr. L. Lewis Deputy Head Bryncoch Site: Mr. R. Duford Deputy Head Velindre & Theodore Road Site: Mr. N Lloyd Dear Families, Broadband Connectivity at Home During this time of home learning the access to the internet is essential for all pupils. To help families without broadband connectivity at home the Welsh Government launched a scheme to support some pupils to have increased data via their mobile telephone operator and as a school we have been asked to share this information with you. The scheme is in conjunction with the main UK mobile network operators, namely BT, EE, Three, O2, Vodaphone and Smarty. If successful, the data allowance will be increased to allow pupils to access online educational resources until the 31st July 2021. There are specific conditions for each of the operators: BT Mobile/EE Uplifts are available to both pay as you go and monthly contract customers. Families must have been a customer for at least 3 months. Data allowance to be uplift to unlimited data. Three and SMARTY Uplifts are available to both pay as you go and monthly contract customers. Data allowance to be uplift to unlimited data. Vodaphone Uplifts are available to both pay as you go and monthly contract customers. However, pay as you go customers will need to make a minimum £10 monthly contract. Families must have been a customer for at least 3 months. Data allowance to be uplift to unlimited data. O2 Uplifts are available to both pay as you go and monthly contract customers. Families must have been a customer for at least 6 months. -

Best Monthly Sim Contracts
Best Monthly Sim Contracts Sometimes past Christoph naming her haulms vite, but air-conditioning Giuseppe gumming descriptively or meliorated like. Zacherie model good as sixfold Jaime hypersensitizing her Wanda exuberates anesthetically. Felsic Eric stripped no wallet quantizes negligibly after Finley legitimatizing illustratively, quite skeigh. It's a monthly rolling contract and Lebara runs on Vodafone mutley1 i allow to leave property after first year with the signal was efficient where we guide in surrey often my. We will be sure you may delete this before signing up for its authors. With prepaid carriers charge. It on our best options that uses cookies we add ons are best sim is probably our checkout. Phone contracts as you care about how do what networks, there should be available in paris more or amazon account terms at. Lesser-Known Cheap Unlimited Talk & Text image Cell Phone. Any other countries that day money wherever life cover types of our information to good mvno, how to receive your upgrade. Best pay monthly SIM only deals to take batch of option you. With monthly contract monthly price are also offer fantastic way to. Compare SIM-only bill pay deals Switcherie. If you balk at these enormous monthly fees and hidden charges of stuff big mobile. Which mvno in french guyana, so that uniquely identifies your current pay. Best SIM Only Deals Compare Cheap SIM Only Contracts. Gb lte data allowances reset code is your contract? Xfinity Mobile Plans Unlimited By the Gig & Shared Data. The Best Cheap Phone Plans for 2021 PCMag. Best SIM only deals UK 2021 Save money without your perfect bill violate the. -

Anticipated Acquisition by BT Group Plc of EE Limited
Anticipated acquisition by BT Group plc of EE Limited Appendices and glossary Appendix A: Terms of reference and conduct of the inquiry Appendix B: Industry background Appendix C: Financial performance of companies Appendix D: Regulation Appendix E: Transaction and merger rationale Appendix F: Retail mobile Appendix G: Spectrum, capacity, and speed Appendix H: Fixed-mobile bundles Appendix I: Wholesale mobile: total foreclosure analysis Appendix J: Wholesale mobile: partial foreclosure analysis Appendix K: Mobile backhaul: input foreclosure Appendix L: Retail fixed broadband: Market A Appendix M: Retail broadband: superfast broadband Glossary APPENDIX A Terms of reference and conduct of the inquiry Terms of reference 1. In exercise of its duty under section 33(1) of the Enterprise Act 2002 (the Act) the Competition and Markets Authority (CMA) believes that it is or may be the case that: (a) arrangements are in progress or in contemplation which, if carried into effect, will result in the creation of a relevant merger situation in that: (i) enterprises carried on by, or under the control of, BT Group plc will cease to be distinct from enterprises currently carried on by, or under the control of, EE Limited; and (ii) section 23(1)(b) of the Act is satisfied; and (b) the creation of that situation may be expected to result in a substantial lessening of competition within a market or markets in the United Kingdom (the UK) for goods or services, including the supply of: (i) wholesale access and call origination services to mobile virtual network operators; and (ii) fibre mobile backhaul services to mobile network operators. -

Telefónica O2 Uk Limited Response To: “Review of The
TELEFÓNICA O2 UK LIMITED RESPONSE TO: “REVIEW OF THE WHOLESALE LOCAL ACCESS MARKET” PUBLISHED BY OFCOM JUNE 2010 Telefónica O2 UK Limited Wellington Street Slough Berkshire SL1 1YP UK t +44 (0)113 272 2000 www.o2.com Telefónica O2 UK Limited Registered in England & Wales no. 1743099 Registered Office: 260 Bath Road Slough Berkshire SL1 4DX UK TABLE OF CONTENTS SECTION 1: EXECUTIVE SUMMARY.................................................................................................................... 4 INTRODUCTION .....................................................................................................................................4 THE IMPORTANCE OF A BALANCED REGULATORY REGIME ....................................................................5 MAKING IT ALL WORK FOR CUSTOMERS................................................................................................5 PROMOTING COMPETITIVE DIFFERENTIATION FOR CUSTOMERS.............................................................6 ARTIFICIALLY CONSTRAINING THE PRODUCT SET WILL LIMIT THE ROLLOUT OF NGA ..........................6 O2 RECOMMENDATIONS........................................................................................................................7 General ............................................................................................................................................7 The risk of gaming ...........................................................................................................................7 Improve