DOCSLIB.ORG

2 Some Definitions in Radiometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2 Some Definitions in Radiometry SOME DEFINITIONS IN RADIOMETRY Sensors on board aircraft or satellites measure and usually quantify the energy received whereas eyes or photographic plates are merely analog receivers. A measurement unit system is therefore required and this shall be defined here. Defining a direction in space The direction of a line through any point on the Earth's surface is defined by 2 angles: • the zenith angle θ, between the zenith (point on the celestial sphere located on the observer's ascending vertical) and the direction observed, • the azimuth angle ϕ between the North (on the local meridian) and the projection of the line on the Earth's surface. The height (altitude or elevation) is sometimes used instead of θ: h = (π / 2) - θ, θ varies along the vertical plane from 0 to π/2 (0° to 90°), ϕ varies along the horizontal plane from 0 to 2 π (0° to 360°). Solid angle A solid angle dΩ delimits a cone in space: d Ω = dS / r2 (in steradians, Sr) where dS is the area cut by the cone over a sphere of radius r the center of which is at the apex of the cone (see figure 4). The solid angle corresponding to all the space around a point equals 4π Sr. The solid angle of a revolving cone for which the plane half-angle at the apex is a equals: Ω = 2π (1 - cos α) Sr. For an observer on Earth, the half-space formed by the celestial arch (in other words an hemisphere) therefore corresponds to 2π Sr ( α = 90°). Radiance*, Emittance, Irradiance * We talk about the radiance of a source and the irradiance at an object (by a source). Be careful: the Earth's surface which receives the irradiance of the Sun, acts like a source for the sensor since it reflects a back part of the solar energy it receives. The objects studied can either emit radiation (radiance, emittance) or be "illuminated" by a source (irradiance). We will therefore require a series of definitions for each of these terms. Before giving the definitions, here's a reminder of the notion of Power: Power (measured in Watts): power is the quantity of energy emitted by an object per unit of time in all directions or received by an object per unit of time from all directions. Definitions on sources Objects emitting electromagnetic waves. a) Point source Intensity: intensity is the power emitted by a point source A per solid angle unit. -1 IA = dW/dΩ (in W.Sr ) If the intensity is the same in all directions, the source is called isotropic. Whenever a source does not have the same power in all directions it is said to be anisotropic. This notion is rarely used in remote sensing, as the Earth's surface observed by satellite is not a point source. b) Extended source Radiance: radiance (L) is the power emitted (dW) per unit of the solid angle (dΩ) and per unit of the projected surface (ds cosθ) of an extended widespread source in a given direction (θ). L = d2W / (dΩ ds cosθ) (in W.Sr-1. m-2) If radiance is not dependent on θ and ϕ, i.e. if is the same in all directions, the source is said to be Lambertian. Ordinary, surfaces are rarely found to be Lambertian. This notion is very important as the energy measured by the sensor is proportional to the radiance of the observed source (Earth's surface). Emittance: emittance (M) is the power emitted (dW) per surface unit of an extended widespread source, throughout an hemisphere. The radiance is therefore integrated along all the directions of a half-space (over an hemisphere). M = dW / dS (in W.m-2) The following relationship is applicable for a Lambertian surface: M = π L According to the definition of radiance: d2W / dS = L cosθ d Ω i.e.: dW / dS = M ∨= L cosθ dΩ Now the element of the solid angle dΩ under which the surface element of a sphere delimited by directions (θ, ϕ) (θ + dθ, ϕ) (θ + dθ, ϕ + dθ) and ( θ, ϕ + dϕ) is: dΩ = sinϕ dθ dϕ Hence the integration over an hemisphere is expressed as follows: 2π π / 2 M = L dϕ cosθ sinθ dθ ∫ ∫0 0 As the first integral equals 2π and the second 1/2, the result is: M = πL This mathematical formulation simply demonstrates that although the solid angle under which the upper hemisphere is viewed is 2π, emittance of a Lambertian surface can be found by multiplying radiance by π. This can be intuitively understood: radiance is defined per unit of visible surface: let's take an element of a Lambertian constant, defined surface: the measurement of the energy emitted by this object will decrease by cos θ like the projected surface when the direction of observation departs from the surface normal. Emittance is a major notion in remote sensing, as a surface element on the Earth re-emits the energy received throughout the hemisphere above the local horizontal plane. Definitions on objects Objects receiving electromagnetic waves (as opposed to sources) Irradiance: this is the power received per surface unit from all directions of a half space (hemisphere). E = dW / dS (in W.m-2) The element of the Earth's surface ds receives an irradiance E from the upper half space and acts for the sensor as a source of radiance L along a direction θ. Remarks: Why is radiance defined as "directional" and irradiance as "hemispheric" ? • the sensor receives energy radiated by the source dS along a specific direction. Radiance is therefore directional; • irradiance of the Earth's surface in the visible range is caused by the Sun. As the latter has a precise position on the celestial arch, we could be led to think irradiance is directional here. This is not at all the case for a simple reason: through the atmosphere which scatters sunlight (more details will be given on scattering later), visible radiation reaches us not only from the direction of the Sun but also from all directions in the upper hemisphere. This is why we can see clearly along a shady street. Consequently, solar irradiance is the sum of all direct and diffuse irradiance and is therefore hemispheric. All the previous definitions can be given for a narrow wavelength range centered around λ. They can be noted that: L(λ), M(λ), E( λ). Summary of Radiometric Terms Radiant flux (W): the amount of radiant energy emitted, transmitted, or received per unit time. Radiant flux density (W/m2): radiant flux per unit area Irradiance (W/m2): radiant flux density incident on a surface Radiant spectral flux density (W m-2 mm-1): radiant flux density per unit of wavelength interval. Radiant intensity (W/sr): flux emanating from a surface per unit solid angle. Radiance (W m-2 sr-1): radiant flux density emanating from a surface per unit solid angle Spectral radiance (W m-2 sr-1 mm-1): radiance per unit wavelength interval. Radiant emittance (W/m2): radiant flux density emitted by a surface. Summary of radiometric terms Radiant energy (J) Add time Radiant flux (J/S = W) Hemispherical Directional Add area Add direction Radiant flux density (W/m2) Radiant intensity(W/sr) Irradiance (incident) Add area Radiant emittance (emitted) Radiance (W m-2 sr-1) Add wavelength Add wavelength Spectral radiance Radiant spectral flux (W m-2 sr-1 mm-1) density (w m-2 mm-1).
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Fundametals of Rendering - Radiometry / Photometry
    Fundametals of Rendering - Radiometry / Photometry “Physically Based Rendering” by Pharr & Humphreys •Chapter 5: Color and Radiometry •Chapter 6: Camera Models - we won’t cover this in class 782 Realistic Rendering • Determination of Intensity • Mechanisms – Emittance (+) – Absorption (-) – Scattering (+) (single vs. multiple) • Cameras or retinas record quantity of light 782 Pertinent Questions • Nature of light and how it is: – Measured – Characterized / recorded • (local) reflection of light • (global) spatial distribution of light 782 Electromagnetic spectrum 782 Spectral Power Distributions e.g., Fluorescent Lamps 782 Tristimulus Theory of Color Metamers: SPDs that appear the same visually Color matching functions of standard human observer International Commision on Illumination, or CIE, of 1931 “These color matching functions are the amounts of three standard monochromatic primaries needed to match the monochromatic test primary at the wavelength shown on the horizontal scale.” from Wikipedia “CIE 1931 Color Space” 782 Optics Three views •Geometrical or ray – Traditional graphics – Reflection, refraction – Optical system design •Physical or wave – Dispersion, interference – Interaction of objects of size comparable to wavelength •Quantum or photon optics – Interaction of light with atoms and molecules 782 What Is Light ? • Light - particle model (Newton) – Light travels in straight lines – Light can travel through a vacuum (waves need a medium to travel in) – Quantum amount of energy • Light – wave model (Huygens): electromagnetic radiation: sinusiodal wave formed coupled electric (E) and magnetic (H) fields 782 Nature of Light • Wave-particle duality – Light has some wave properties: frequency, phase, orientation – Light has some quantum particle properties: quantum packets (photons). • Dimensions of light – Amplitude or Intensity – Frequency – Phase – Polarization 782 Nature of Light • Coherence - Refers to frequencies of waves • Laser light waves have uniform frequency • Natural light is incoherent- waves are multiple frequencies, and random in phase.
    [Show full text]
  • Light and Illumination
    ChapterChapter 3333 -- LightLight andand IlluminationIllumination AAA PowerPointPowerPointPowerPoint PresentationPresentationPresentation bybyby PaulPaulPaul E.E.E. Tippens,Tippens,Tippens, ProfessorProfessorProfessor ofofof PhysicsPhysicsPhysics SouthernSouthernSouthern PolytechnicPolytechnicPolytechnic StateStateState UniversityUniversityUniversity © 2007 Objectives:Objectives: AfterAfter completingcompleting thisthis module,module, youyou shouldshould bebe ableable to:to: •• DefineDefine lightlight,, discussdiscuss itsits properties,properties, andand givegive thethe rangerange ofof wavelengthswavelengths forfor visiblevisible spectrum.spectrum. •• ApplyApply thethe relationshiprelationship betweenbetween frequenciesfrequencies andand wavelengthswavelengths forfor opticaloptical waves.waves. •• DefineDefine andand applyapply thethe conceptsconcepts ofof luminousluminous fluxflux,, luminousluminous intensityintensity,, andand illuminationillumination.. •• SolveSolve problemsproblems similarsimilar toto thosethose presentedpresented inin thisthis module.module. AA BeginningBeginning DefinitionDefinition AllAll objectsobjects areare emittingemitting andand absorbingabsorbing EMEM radiaradia-- tiontion.. ConsiderConsider aa pokerpoker placedplaced inin aa fire.fire. AsAs heatingheating occurs,occurs, thethe 1 emittedemitted EMEM waveswaves havehave 2 higherhigher energyenergy andand 3 eventuallyeventually becomebecome visible.visible. 4 FirstFirst redred .. .. .. thenthen white.white. LightLightLight maymaymay bebebe defineddefineddefined
    [Show full text]
  • About SI Units
    Units SI units: International system of units (French: “SI” means “Système Internationale”) The seven SI base units are: Mass: kg Defined by the prototype “standard kilogram” located in Paris. The standard kilogram is made of Pt metal. Length: m Originally defined by the prototype “standard meter” located in Paris. Then defined as 1,650,763.73 wavelengths of the orange-red radiation of Krypton86 under certain specified conditions. (Official definition: The distance traveled by light in vacuum during a time interval of 1 / 299 792 458 of a second) Time: s The second is defined as the duration of a certain number of oscillations of radiation coming from Cs atoms. (Official definition: The second is the duration of 9,192,631,770 periods of the radiation of the hyperfine- level transition of the ground state of the Cs133 atom) Current: A Defined as the current that causes a certain force between two parallel wires. (Official definition: The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 meter apart in vacuum, would produce between these conductors a force equal to 2 × 10-7 Newton per meter of length. Temperature: K One percent of the temperature difference between boiling point and freezing point of water. (Official definition: The Kelvin, unit of thermodynamic temperature, is the fraction 1 / 273.16 of the thermodynamic temperature of the triple point of water. Amount of substance: mol The amount of a substance that contains Avogadro’s number NAvo = 6.0221 × 1023 of atoms or molecules.
    [Show full text]
  • Black Body Radiation and Radiometric Parameters
    Black Body Radiation and Radiometric Parameters: All materials absorb and emit radiation to some extent. A blackbody is an idealization of how materials emit and absorb radiation. It can be used as a reference for real source properties. An ideal blackbody absorbs all incident radiation and does not reflect. This is true at all wavelengths and angles of incidence. Thermodynamic principals dictates that the BB must also radiate at all ’s and angles. The basic properties of a BB can be summarized as: 1. Perfect absorber/emitter at all ’s and angles of emission/incidence. Cavity BB 2. The total radiant energy emitted is only a function of the BB temperature. 3. Emits the maximum possible radiant energy from a body at a given temperature. 4. The BB radiation field does not depend on the shape of the cavity. The radiation field must be homogeneous and isotropic. T If the radiation going from a BB of one shape to another (both at the same T) were different it would cause a cooling or heating of one or the other cavity. This would violate the 1st Law of Thermodynamics. T T A B Radiometric Parameters: 1. Solid Angle dA d r 2 where dA is the surface area of a segment of a sphere surrounding a point. r d A r is the distance from the point on the source to the sphere. The solid angle looks like a cone with a spherical cap. z r d r r sind y r sin x An element of area of a sphere 2 dA rsin d d Therefore dd sin d The full solid angle surrounding a point source is: 2 dd sind 00 2cos 0 4 Or integrating to other angles < : 21cos The unit of solid angle is steradian.
    [Show full text]
  • Section 22-3: Energy, Momentum and Radiation Pressure
    Answer to Essential Question 22.2: (a) To find the wavelength, we can combine the equation with the fact that the speed of light in air is 3.00 " 108 m/s. Thus, a frequency of 1 " 1018 Hz corresponds to a wavelength of 3 " 10-10 m, while a frequency of 90.9 MHz corresponds to a wavelength of 3.30 m. (b) Using Equation 22.2, with c = 3.00 " 108 m/s, gives an amplitude of . 22-3 Energy, Momentum and Radiation Pressure All waves carry energy, and electromagnetic waves are no exception. We often characterize the energy carried by a wave in terms of its intensity, which is the power per unit area. At a particular point in space that the wave is moving past, the intensity varies as the electric and magnetic fields at the point oscillate. It is generally most useful to focus on the average intensity, which is given by: . (Eq. 22.3: The average intensity in an EM wave) Note that Equations 22.2 and 22.3 can be combined, so the average intensity can be calculated using only the amplitude of the electric field or only the amplitude of the magnetic field. Momentum and radiation pressure As we will discuss later in the book, there is no mass associated with light, or with any EM wave. Despite this, an electromagnetic wave carries momentum. The momentum of an EM wave is the energy carried by the wave divided by the speed of light. If an EM wave is absorbed by an object, or it reflects from an object, the wave will transfer momentum to the object.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Properties of Electromagnetic Waves Any Electromagnetic Wave Must Satisfy Four Basic Conditions: 1
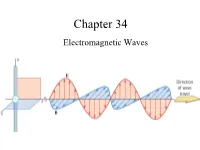
    Chapter 34 Electromagnetic Waves The Goal of the Entire Course Maxwell’s Equations: Maxwell’s Equations James Clerk Maxwell •1831 – 1879 •Scottish theoretical physicist •Developed the electromagnetic theory of light •His successful interpretation of the electromagnetic field resulted in the field equations that bear his name. •Also developed and explained – Kinetic theory of gases – Nature of Saturn’s rings – Color vision Start at 12:50 https://www.learner.org/vod/vod_window.html?pid=604 Correcting Ampere’s Law Two surfaces S1 and S2 near the plate of a capacitor are bounded by the same path P. Ampere’s Law states that But it is zero on S2 since there is no conduction current through it. This is a contradiction. Maxwell fixed it by introducing the displacement current: Fig. 34-1, p. 984 Maxwell hypothesized that a changing electric field creates an induced magnetic field. Induced Fields . An increasing solenoid current causes an increasing magnetic field, which induces a circular electric field. An increasing capacitor charge causes an increasing electric field, which induces a circular magnetic field. Slide 34-50 Displacement Current d d(EA)d(q / ε) 1 dq E 0 dt dt dt ε0 dt dq d ε E dt0 dt The displacement current is equal to the conduction current!!! Bsd μ I μ ε I o o o d Maxwell’s Equations The First Unified Field Theory In his unified theory of electromagnetism, Maxwell showed that electromagnetic waves are a natural consequence of the fundamental laws expressed in these four equations: q EABAdd 0 εo dd Edd s BE B s μ I μ ε dto o o dt QuickCheck 34.4 The electric field is increasing.
    [Show full text]
  • Extraction of Incident Irradiance from LWIR Hyperspectral Imagery Pierre Lahaie, DRDC Valcartier 2459 De La Bravoure Road, Quebec, Qc, Canada
    DRDC-RDDC-2015-P140 Extraction of incident irradiance from LWIR hyperspectral imagery Pierre Lahaie, DRDC Valcartier 2459 De la Bravoure Road, Quebec, Qc, Canada ABSTRACT The atmospheric correction of thermal hyperspectral imagery can be separated in two distinct processes: Atmospheric Compensation (AC) and Temperature and Emissivity separation (TES). TES requires for input at each pixel, the ground leaving radiance and the atmospheric downwelling irradiance, which are the outputs of the AC process. The extraction from imagery of the downwelling irradiance requires assumptions about some of the pixels’ nature, the sensor and the atmosphere. Another difficulty is that, often the sensor’s spectral response is not well characterized. To deal with this unknown, we defined a spectral mean operator that is used to filter the ground leaving radiance and a computation of the downwelling irradiance from MODTRAN. A user will select a number of pixels in the image for which the emissivity is assumed to be known. The emissivity of these pixels is assumed to be smooth and that the only spectrally fast varying variable in the downwelling irradiance. Using these assumptions we built an algorithm to estimate the downwelling irradiance. The algorithm is used on all the selected pixels. The estimated irradiance is the average on the spectral channels of the resulting computation. The algorithm performs well in simulation and results are shown for errors in the assumed emissivity and for errors in the atmospheric profiles. The sensor noise influences mainly the required number of pixels. Keywords: Hyperspectral imagery, atmospheric correction, temperature emissivity separation 1. INTRODUCTION The atmospheric correction of thermal hyperspectral imagery aims at extracting the temperature and the emissivity of the material imaged by a sensor in the long wave infrared (LWIR) spectral band.
    [Show full text]
  • RADIANCE® ULTRA 27” Premium Endoscopy Visualization
    EW NNEW RADIANCE® ULTRA 27” Premium Endoscopy Visualization The Radiance® Ultra series leads the industry as a revolutionary display with the aim to transform advanced visualization technology capabilities and features into a clinical solution that supports the drive to improve patient outcomes, improve Optimized for endoscopy applications workflow efficiency, and lower operating costs. Advanced imaging capabilities Enhanced endoscopic visualization is accomplished with an LED backlight technology High brightness and color calibrated that produces the brightest typical luminance level to enable deep abdominal Cleanable splash-proof design illumination, overcoming glare and reflection in high ambient light environments. Medi-Match™ color calibration assures consistent image quality and accurate color 10-year scratch-resistant-glass guarantee reproduction. The result is outstanding endoscopic video image performance. ZeroWire® embedded receiver optional With a focus to improve workflow efficiency and workplace safety, the Radiance Ultra series is available with an optional built-in ZeroWire receiver. When paired with the ZeroWire Mobile battery-powered stand, the combination becomes the world’s first and only truly cordless and wireless mobile endoscopic solution (patent pending). To eliminate display scratches caused by IV poles or surgical light heads, the Radiance Ultra series uses scratch-resistant, splash-proof edge-to-edge glass that includes an industry-exclusive 10-year scratch-resistance guarantee. RADIANCE® ULTRA 27” Premium Endoscopy
    [Show full text]
  • STHF-R Ultra High Flux Gamma Probe Data Sheet
    Features STHF-R™ Ultra High ■ Measurement of H*(10) Flux Gamma Probe ambient gamma dose equivalent rate up to 1000 Sv/h (100 000 R/h) Description ■ To be connected to The STHF-R ultra high flux Radiagem™, MIP 10 Digital™ probe is designed for the or Avior ® meters measurements of very high ■ Waterproof: 80 m (262.5 ft) gamma dose-equivalent rates water depth up to 1000 Sv/h. ■ Detector: Silicon diode This probe is especially ■ 5 kSv maximum integrated designed for ultra high flux dose measurement which can be found in pools in nuclear ■ Compact portable design for power plants or in recycling detector and detector cable facilities. Effectively this on reel probes box is stainless steel based and waterproof up to 80 m (164 ft) underwater. It can be laid underwater in the storage pools Borated water. An optional ballast weight can be supplied to ease underwater measurements. The STHF-R probe is composed of two matched units: ■ The measurement probe including the silicon diode and the associated analog electronics. ■ An interface case which houses the processing electronics that are more sensitive to radiation; this module can be remotely located up to 50 m (164 ft) from the measurement spot. ■ An intermediate connection point with 50 m length cable to which the interface case can be connected. The STHF-R probe can be connected directly to Avior, Radiagem or MIP 10 Digital meters. The STHF-R unit receives power from the survey meter during operation. STHF-R instruments include key components of hardware circuitry (high voltage power supply, amplifier, discriminator, etc.).
    [Show full text]