DOCSLIB.ORG

Orthogonal Frequency Division Multiplexing Multiple-Input Multiple-Output Automotive Radar with Novel Signal Processing Algorithms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Orthogonal Frequency Division Multiplexing Multiple-Input Multiple-Output Automotive Radar with Novel Signal Processing Algorithms Orthogonal Frequency Division Multiplexing Multiple-Input Multiple-Output Automotive Radar with Novel Signal Processing Algorithms von der Fakultät Informatik, Elektrotechnik und Informationstechnik der Universität Stuttgart zur Erlangung der Würde eines Doktor-Ingenieurs (Dr.-Ing.) genehmigte Abhandlung vorgelegt von Gor Hakobyan aus Jerewan, Armenien Hauptberichter: Prof. Dr.-Ing. Bin Yang Mitberichter: Prof. Dr. Friedrich K. Jondral Tag der mündlichen Prüfung: 07.02.2018 Institut für Signalverarbeitung und Systemtheorie der Universität Stuttgart 2018 – 3 – Vorwort Die vorliegende Arbeit entstand während meiner Zeit als Doktorand bei der zentralen Forschung der Robert Bosch GmbH in Kooperation mit der Universität Stuttgart. Mein besonderer Dank gilt Prof. Bin Yang, dem Leiter des Instituts für Signalverarbeitung und Systemtheorie an der Universität Stuttgart für die Gelegenheit, unter seiner Betreuung zu promovieren. Insbesondere möchte ich mich für das Vertrauen, die stets hervorragende Betreuung, die Freiheit, eigene Wege in Forschung zu gehen, sowie kurzfristige und sorgfältige Korrekturen meiner Veröffentlichungen und der Dissertation recht herzlich bedanken. Prof. Friedrich Jondral vom Institut für Nachrichtentechnik des Karlsruher Instituts für Technologie danke ich herzlich für die Übernahme des Mitberichts. Ferner möchte ich mich bei den Mitarbeitern der Robert Bosch GmbH und des Instituts für Signalverarbeitung und Systemtheorie bedanken, die zur Entstehung dieser Arbeit beigetragen haben. Insbesondere geht mein Dank an Herrn Siegbert Steinlechner für die fachliche Betreuung, Mentoring, sowie den Freiraum bei der Ausgestaltung der Arbeit. Seine vielseitige und zugleich tiefgründige Kompetenz in fachlichen und außer fachlichen Bereichen diente als Vorbild und hat zu meiner Weiterentwicklung wesentlich beigetragen. Des weiteren geht mein besonderer Dank an Dr. Michael Schoor für die fachlichen Diskussionen, die zur Vertiefung meines Wissens reichlich beigetragen haben, sowie an Herrn Karim Armanious und an Frau Mekdes Girma für die fruchtbare Zusammenarbeit. Mein Dank gilt ferner allen, die die Dissertation mit großer Sorgfalt und in kurzer Zeit Korrektur gelesen haben: Herrn Siegbert Steinlechner, Dr. Vladimir Petkov, Dr. Jo Pletinckx, Dr. Michael Schoor und Tim Poguntke. Schließlich möchte ich einen ganz besonderen Dank an meine Familie richten, meinen Vater Varazdat Hakobyan, meine Mutter Karine Khachatryan, meinen Bruder Hayk Hakobyan, sowie meine Partnerin Anna Gosk, die mich auf meinem Weg mit stets liebevollen Unterstützung, Ermutigung und Geduld begleitet haben. Ihnen widme ich diese Arbeit. Stuttgart, April 2018 Gor Hakobyan – 5 – Contents List of Symbols and Abbreviations 9 Abstract 15 Zusammenfassung 17 1. Introduction 19 1.1. Background . 19 1.2. Research Objectives . 20 1.3. Contributions and Outline of the Work . 21 2. Automotive Radar 25 2.1. The Radar Principle . 25 2.1.1. Propagation of Radar Signals . 25 2.1.2. Distance Estimation . 27 2.1.3. Velocity Estimation . 28 2.1.4. DOA Estimation . 28 2.2. State-of-the-Art Automotive Radar Systems . 29 2.2.1. FMCW Radar . 29 2.2.2. Fast-Chirp Radar . 31 2.3. OFDM Radar . 33 2.3.1. OFDM Radar Fundamentals . 33 2.3.2. System Parametrization . 40 2.3.3. CP-OFDM vs. RS-OFDM . 43 2.3.4. Methods for Reduction of PAPR for OFDM Radar . 44 2.4. MIMO Radar . 45 2.4.1. Improved DOA Estimation Based on MIMO Array Processing . 45 2.4.2. Multiplexing of Tx Antennas for MIMO Radar . 46 2.4.3. Multichannel Radar Signal Processing . 47 2.5. Comparison of Digital OFDM Radar to Traditional Fast-Chirp Radar . 48 3. OFDM Radar Signal Model and Signal Processing 51 3.1. Signal Model . 52 3.1.1. Continuous-Time Signal Model . 52 3.1.2. Discrete-Time Signal Model . 54 3.1.3. Signal Model in Matrix Notation . 55 3.2. Classical OFDM Radar Signal Processing . 56 3.2.1. State-of-the-Art Signal Processing Methods for OFDM Radar . 56 3.2.2. Description of the Classical OFDM Radar Processing . 58 3.2.3. Performance of the Classical OFDM Radar Processing . 61 – 6 – 3.3. All-Cell Doppler Correction (ACDC) for ICI-Free OFDM Signal Processing . 64 3.3.1. Requirements for All-Cell Doppler Correction . 65 3.3.2. ACDC based Distance-Velocity Estimation . 65 3.3.3. ACDC based OFDM Radar and Communication System . 69 3.3.4. Simulative Analysis . 71 3.3.5. Concluding Remarks . 74 3.4. All-Cell Migration Compensation (ACMC) for Migration-Free Range-Doppler Processing . 75 3.4.1. State-of-the-Art Methods for Range and Doppler Frequency Migration Compensation . 76 3.4.2. Range and Doppler Frequency Migration . 78 3.4.3. All-Cell Migration Compensation based Range-Doppler processing . 79 3.4.4. ACMC Implementation based on Chirp Z-Transform . 81 3.4.5. Simulative Analysis . 82 3.4.6. Concluding Remarks . 85 3.5. Combination of ACDC and ACMC and Comparison to the Classical Signal Processing . 87 4. OFDM-MIMO Radar 89 4.1. Conventional Multiplexing Methods Applied to OFDM-MIMO Radar . 89 4.1.1. Time Division Multiplexing . 90 4.1.2. Frequency Division Multiplexing . 91 4.1.3. Code Division Multiplexing . 91 4.2. OFDM-MIMO Radar Multiplexed via Equidistant Subcarrier Interleaving . 92 4.3. OFDM-MIMO Radar Multiplexed via Non-Equidistant Subcarrier Interleaving 93 4.3.1. Non-Equidistant Subcarrier Interleaving (NeqSI) . 94 4.3.2. Non-Equidistant Dynamic Subcarrier Interleaving (NeqDySI) . 96 4.4. Optimization of the Interleaving Pattern for Non-Equidistant Interleaving Schemes100 4.4.1. Genetic Algorithms . 100 4.4.2. Formulation of the Optimization Task . 102 4.4.3. Effect of Windowing on the PSL of Non-Equidistant Sampling . 104 4.4.4. Optimization Results for Non-Equidistant Interleaving Schemes . 105 4.5. Application of Sparse Recovery Methods for OFDM-MIMO Radar . 106 4.5.1. Compressed Sensing Overview . 107 4.5.2. Fundamentals of Compressed Sensing . 108 4.5.3. CS based Distance-Velocity Estimation . 114 4.5.4. Simulative Analysis . 119 4.6. Concluding Remarks . 122 5. Interference Mitigation Techniques for OFDM Radar 125 5.1. Influence of Interference on OFDM Radar . 125 5.2. A Narrowband Interference Suppression Method for OFDM Radar . 128 5.2.1. Interference Suppression Algorithm . 128 5.2.2. Simulative Analysis . 130 5.3. OFDM Radar Networks and Methods for Mitigation of OFDM Interference . 132 5.4. Interference-Aware Cognitive OFDM Radar . 133 5.4.1. Cognitive Radar . 134 – 7 – 5.4.2. Waveform Adaptation Methods for Cognitive Radar . 136 5.4.2.1. Carrier Frequency Hopping – Waveform Adaptation . 137 5.4.2.2. Slow-Time Chirp Waveform Adaptation (STC-WA) with Vari- able Symbol Repetition Intervals . 138 5.4.3. Spectrum Sensing . 145 5.5. Concluding Remarks . 147 6. OFDM-MIMO Radar Prototype and Experimental Validation of the Proposed Methods 149 6.1. Description of the System Prototype . 149 6.2. Measurements for Performance Verification of the System Prototype . 153 6.2.1. Measurements in an Anechoic Chamber . 153 6.2.2. Measurements in a Road Scenario . 155 6.3. Experimental Validation of the Proposed Distance-Velocity Estimation Algorithms156 6.3.1. Validation of ACDC in a Road Scenario . 156 6.3.2. Validation of ACMC in a Road Scenario . 159 6.4. Experimental Validation of the Proposed Multiplexing Methods for OFDM- MIMO Radar . 161 6.4.1. Validation of the NeqDySI Multiplexing . 161 6.4.2. Validation of the NeqSI Multiplexing with Sparse Iterative Multidimen- sional Frequency Estimation (SIMFE) Based Processing . 161 6.5. Experimental Validation of the Proposed Interference Mitigation Techniques . 163 6.5.1. Validation of the Proposed Narrowband Interference Suppression Method 163 6.5.2. Verification of the Waveform Adaptation Properties of STC-WA for Cognitive Interference Avoidance . 164 6.6. Concluding Remarks . 167 7. Conclusions 169 7.1. Summary of Key Contributions . 169 7.2. Outlook . 171 A. ACMC Description Based on a Frequency Domain Signal Model 173 B. Estimation Parameters of STC-WA 175 – 9 – List of Symbols and Abbreviations Notation x Scalar x Column vector x Matrix X Set Mathematical Operations x∗ Complex conjugate xT ; xT Transpose of a vector x or a matrix x xH ; xH Hermitian transpose of a vector x or a matrix x jxj Amplitude of a scalar, cardinality of a set kxk `2-norm of a vector kxkp `p-norm of a vector x−1 Inverse of a matrix x+ Moore–Penrose pseudoinverse of a matrix x y Hadamard (elementwise) product of matrices x and y x : / y Elementwise division of matrices x and y hx;yi Scalar (inner) product of vectors x and y diag(x) Diagonal matrix containing the elements of the vector x ¯ ¯ DN (f) Diagonal matrix containing elements of exp(j2πfn); n 2 [0;N − 1] N (x) Nullspace of the matrix x supp(x) Support of a vector x rect(t=T ) Rectangular function of the duration T ΣK Set of all K-sparse signals r Nabla operator r = @ ;:::; @ @x1 @xN F(·) Fourier transform – 10 – F −1(·) Inverse Fourier transform min(·) Minimum with respect to x x max(·) Maximum with respect to x x arg min(·) Argument x, for which the minimum is obtained x arg max(·) Argument x, for which the maximum is obtained x x y Assignment of y to x Frequently Used Symbols a; a¯ Real and complex target amplitudes B Bandwidth B Vector of the magnetic field B Doppler scaling matrix c Speed of propagation of electromagnetic waves c0 Speed of light d Distance of the target du Unambiguous distance range ∆d Distance resolution E Vector of the electric field fc Carrier frequency fc,a Adaptive carrier frequency fD Doppler frequency ¯ fD Normalized Doppler frequency fn Frequency of the n-th OFDM subcarrier FN Matrix of
Load more

Recommended publications
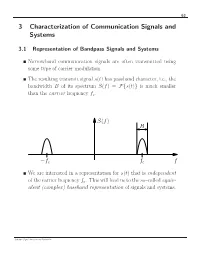
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders
    /7 7.3.5 Fiber-Optic Cables (FO) 7.3.6 Telephone Company Unes (TELCO) 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders 7.4 Transmission Security 8. Consumer Equipment Issues 8.1 Complexity of Receivers 8.2 Receiver Input/Output Characteristics 8.2.1 RF Interface 8.2.2 Baseband Video Interface 8.2.3 Baseband Audio Interface 8.2.4 Interfacing with Ancillary Signals 8.2.5 Receiver Antenna Systems Requirements 8.3 Compatibility with Existing NTSC Consumer Equipment 8.3.1 RF Compatibility 8.3.2 Baseband Video Compatibility 8.3.3 Baseband Audio Compatibility 8.3.4 IDTV Receiver Compatibility 8.4 Allows Multi-Standard Display Devices 9. Other Considerations 9.1 Practicality of Near-Term Technological Implementation 9.2 Long-Term Viability/Rate of Obsolescence 9.3 Upgradability/Extendability 9.4 Studio/Plant Compatibility Section B: EXPLANATORY NOTES OF ATTRIBUTES/SYSTEMS MATRIX Items on the Attributes/System Matrix for which no explanatory note is provided were deemed to be self-explanatory. I. General Description (Proponent) section I shall be used by a system proponent to define the features of the system being proposed. The features shall be defined and organized under the headings ot the following subsections 1 through 4. section I. General Description (Proponent) shall consist of a description of the proponent system in narrative form, which covers all of the features and characteris­ tics of the system which the proponent wishe. to be included in the public record, and which will be used by various groups to analyze and understand the system proposed, and to compare with other propo.ed systems.
    [Show full text]
  • Tracking Non-Cooperative Low Earth Orbit Objects Using GNSS Satellites As a Multi-Static Radar
    Tracking non-cooperative low earth orbit objects using GNSS satellites as a multi-static radar Md Sohrab Mahmud Andrew Lambert Craig Benson [email protected] [email protected] [email protected] School of Engineering and Information Technology University of New South Wales, Canberra Abstract Space debris is a growing hazard since space activity and the amount of space debris are both increasing. If the risks posed by space object collisions cannot be mitigated, this will hinder the future use of space. Accurate knowledge of the trajectory and behavior of satellites and debris is required to mitigate collision risks as the density of space objects increases. This requires space object tracking systems that are both affordable and scale well for very large numbers of objects under observation. Wide field of view, all-weather, passive systems scale well for reliable surveillance of very large numbers of objects. Global Navigation Satellite System (GNSS) satellites have been proposed as potential illuminators of opportunity to track Low Earth Orbit (LEO) debris, paired with ground-based receivers in a bistatic arrangement. In this paper, we discuss the signal characteristics used in these observations, the results of recent relevant laboratory-based experiments, simulation work performed in preparation for on-orbit experiments of these techniques, and our plans for the development of a system capable of tracking LEO debris to enhance space situational awareness. Introduction Space debris is an existing and growing problem for active satellites and future space missions. Since the first ever space mission, Sputnik 1, up to now, the number of tracked objects as small as 10 cm is catalogued as 43,931 (Kelso, 2018).
    [Show full text]
  • Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System
    Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System Kang Hsia Abstract: Telecommunications industry has widely adopted single sideband (SSB or complex quadrature) transmitter and receiver system, and one popular implementation for SSB system is to achieve image rejection through quadrature component image cancellation. Typically, during the SSB system characterization, the baseband fundamental tone and also the harmonic distortion products are important parameters besides image and LO feedthrough leakage. To ensure accurate characterization, the actual frequency locations of the harmonic distortion products are critical. While system designers may be tempted to assume that the harmonic distortion products are simply up-converted in the same fashion as the baseband fundamental frequency component, the actual distortion products may have surprising results and show up on the different side of spectrum. This paper discusses the theory of SSB system and the actual location of the baseband harmonic distortion products. Introduction Communications engineers have utilized SSB transmitter and receiver system because it offers better bandwidth utilization than double sideband (DSB) transmitter system. The primary cause of bandwidth overhead for the double sideband system is due to the image component during the mixing process. Given data transmission bandwidth of B, the former requires minimum bandwidth of B whereas the latter requires minimum bandwidth of 2B. While the filtering of the image component is one type of SSB implementation, another type of SSB system is to create a quadrature component of the signal and ideally cancels out the image through phase cancellation. M(t) M(t) COS(2πFct) Baseband Message Signal (BB) Modulated Signal (RF) COS(2πFct) Local Oscillator (LO) Signal Figure 1.
    [Show full text]
  • Prof. Hugh Griffiths
    Passive Radar - From Inception to Maturity Hugh Griffiths Senior Past President, IEEE AES Society 2017 IEEE Picard Medal IEEE AESS Distinguished Lecturer THALES / Royal Academy of Engineering Chair of RF Sensors University College London Radar Symposium, Ben-Gurion University of the Negev, 13 February 2017 OUTLINE • Introduction and definitions • Some history • Bistatic radar properties: geometry, radar equation, target properties • Passive radar illuminators • Passive radar systems and results • The future … 2 BISTATIC RADAR: DEFINITIONS MONOSTATIC RADAR MULTILATERATION RADAR Tx & Rx at same, or nearly Radar net using range-only data the same, location MULTISTATIC RADAR BISTATIC RADAR Bistatic radar net with multiple Txs Tx & Rx separated by a and/or RXs. considerable distance in order to achieve a technical, operational or cost benefit HITCHHIKER Bistatic Rx operating with the Tx of a monostatic radar RADAR NET Several radars linked together to improve PASSIVE BISTATIC RADAR coverage* or accuracy Bistatic Rx operating with other Txs of opportunity * Enjoys the union of individual coverage areas. All others 3 require the intersection of individual coverage areas. Coverage area: (SNR + BW + LOS) 3 BISTATIC RADAR • Bistatic radar has potential advantages in detection of stealthy targets which are shaped to scatter energy in directions away from the monostatic • The receiver is covert and therefore safer in many situations • Countermeasures are difficult to deploy against bistatic radar • Increasing use of systems based on unmanned air vehicles (UAVs) makes bistatic systems attractive • Many of the synchronisation and geolocation problems that were previously very difficult are now readily soluble using GPS, and • The extra degrees of freedom may make it easier to extract information from bistatic clutter for remote sensing applications 4 4 BISTATIC RADAR • The first radars were bistatic (till T/R switches were invented) • First resurgence (1950 – 1960): semi-active homing missiles, SPASUR, ….
    [Show full text]
  • P-180U and MARS-L Radar Purchase from Ukraine and Turaf PYAS
    P-180U and MARS-L Radar Purchase from Ukraine and TuRAF PYAS Project by İbrahim SÜNNETÇİ According to Ukrainian based combined PSR/ the SSR channel, is given the P-18MA/P-180U radar press, Ukrspetsexport SSR (Primary and as 5,000 hours. system, which is also used (the only institution Secondary Surveillance by the Ukrainian Armed authorized by the Radar) system. The The ground-based VHF Forces, could detect the Ukrainian Government to combined use of primary (metric band) P-180U F-117A Nighthawk Stealth fulfill the export potential and secondary channels (P-18MA) is a long- Fighter from 61km. of Ukraine's military- considerably increases range surveillance radar industrial complex), a the detection range and which provides the radar There are different subsidiary of the Ukrainian accuracy of finding the information and flight speculations regarding state-owned defense coordinates of aerial routes of aerial objects. the procurement company UkroBoronProm objects. Additionally, the The solid-state P-180U of the MARS-L and (UOP), delivered two availability of additional is the modernized and P-180U radars, which P-180U and two MARS-L aircraft information improved version of are considered to be radars to SSTEK Defense such as current altitude, the VHF-Band 2D (two- capable of detecting Industry Technologies in remaining fuel, condition dimensional, provides only stealth aircraft as they late December 2019, under of the onboard systems, azimuth and range data) operate on the L and VHF a contract worth US$11,144 etc., together with P-18 early warning radar bands, by SSTEK Defense million. According to the primary radar information, developed during the Industry Technologies, reports, the total cost of significantly increases Soviet Union.
    [Show full text]
  • Baseband Video Testing with Digital Phosphor Oscilloscopes
    Application Note Baseband Video Testing With Digital Phosphor Oscilloscopes Video signals are complex pose instrument that can pro- This application note demon- waveforms comprised of sig- vide accurate information – strates the use of a Tektronix nals representing a picture as quickly and easily. Finally, to TDS 700D-series Digital well as the timing informa- display all of the video wave- Phosphor Oscilloscope to tion needed to display the form details, a fast acquisi- make a variety of common picture. To capture and mea- tion technology teamed with baseband video measure- sure these complex signals, an intensity-graded display ments and examines some of you need powerful instru- give the confidence and the critical measurement ments tailored for this appli- insight needed to detect and issues. cation. But, because of the diagnose problems with the variety of video standards, signal. you also need a general-pur- Copyright © 1998 Tektronix, Inc. All rights reserved. Video Basics Video signals come from a for SMPTE systems, etc. The active portion of the video number of sources, including three derived component sig- signal. Finally, the synchro- cameras, scanners, and nals can then be distributed nization information is graphics terminals. Typically, for processing. added. Although complex, the baseband video signal Processing this composite signal is a sin- begins as three component gle signal that can be carried analog or digital signals rep- In the processing stage, video on a single coaxial cable. resenting the three primary component signals may be combined to form a single Component Video Signals. color elements – the Red, Component signals have an Green, and Blue (RGB) com- composite video signal (as in NTSC or PAL systems), advantage of simplicity in ponent signals.
    [Show full text]
  • Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
    Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse.
    [Show full text]
  • China's Strategic Modernization: Implications for the United States
    CHINA’S STRATEGIC MODERNIZATION: IMPLICATIONS FOR THE UNITED STATES Mark A. Stokes September 1999 ***** The views expressed in this report are those of the author and do not necessarily reflect the official policy or position of the Department of the Army, the Department of the Air Force, the Department of Defense, or the U.S. Government. This report is cleared for public release; distribution is unlimited. ***** Comments pertaining to this report are invited and should be forwarded to: Director, Strategic Studies Institute, U.S. Army War College, 122 Forbes Ave., Carlisle, PA 17013-5244. Copies of this report may be obtained from the Publications and Production Office by calling commercial (717) 245-4133, FAX (717) 245-3820, or via the Internet at [email protected] ***** Selected 1993, 1994, and all later Strategic Studies Institute (SSI) monographs are available on the SSI Homepage for electronic dissemination. SSI’s Homepage address is: http://carlisle-www.army. mil/usassi/welcome.htm ***** The Strategic Studies Institute publishes a monthly e-mail newsletter to update the national security community on the research of our analysts, recent and forthcoming publications, and upcoming conferences sponsored by the Institute. Each newsletter also provides a strategic commentary by one of our research analysts. If you are interested in receiving this newsletter, please let us know by e-mail at [email protected] or by calling (717) 245-3133. ISBN 1-58487-004-4 ii CONTENTS Foreword .......................................v 1. Introduction ...................................1 2. Foundations of Strategic Modernization ............5 3. China’s Quest for Information Dominance ......... 25 4.
    [Show full text]
  • Regulation on Collective Frequencies for Licence-Exempt Radio Transmitters and on Their Use
    FICORA 15 AIH/2015 M 1 (22) Unofficial translation Regulation on collective frequencies for licence-exempt radio transmitters and on their use Issued in Helsinki on 6 February 2015 The Finnish Communications Regulatory Authority (FICORA) has, under section 39(3 and 4) of the Information Society Code of 7 November 2014 (917/2014), laid down: Chapter 1 General provisions Section 1 The oObjective of the Regulation This Regulation lays down provisions on collective frequencies for as well as use and registration of such radio transmitters whose conformity with requirements has been attested in such a way as laid down in the Information Society Code, and for the possession and use of which a radio licence is not required. Section 2 Scope of application This Regulation applies to the following radio transmitters which operate only on the collective frequencies assigned in this Regulation and whose conformity with requirements has been attested in such a way as mentioned in section 257 or section 352 of the Information Society Code: 1) cordless CT1 telephones taken into use on 31 December 2003 at the latest, cordless CT2 telephones taken into use on 31 December 2004 at the latest, and DECT equipment; 2) mobile terminals and other terminals for GSM, UMTS, digital broadband mobile networks and terrestrial systems capable of providing electronic communications services; 3) LA telephones (national Citizen Band equipment) which have been approved according to the regulations of 25 March 1981 by the General Directorate of Posts and Telecommunications
    [Show full text]
  • Bistatic Radar with Thinned Receiving Phased Array for Airports Surveillance
    BISTATIC RADAR WITH THINNED RECEIVED PHASED ARRAY M. Cherniakov University of Birmingham Edgbaston, B15 2TT, UK [email protected] Abstract The presented concept of bistatic radar can have significant benefit for airport surveillance. It may be described as a bistatic semi-active radar which utilizes one of the available airport area surveillance radars as the transmitter and a receiving only, slave radar. The passive radar contains an electronically scanned antenna phased array which is essentially thinned. The grating lobes are suppressed in this system by the transmitting radar acting as a space filter. At the conceptual level of the paper the advantages and limitations of the proposed radar architecture are considered. 1 Introduction The primary goal of this conceptual paper is to introduce the topology and basic performance analysis of bistatic radar (BR) with essentially different transmitting and receiving antennas. This BR can be described as bistatic semi-active radar that utilize as the illuminator (transmitter) one of the available surveillance radars (master radar - MR) and a passive, receiving only, radar (slave radar - SR). Presumably MR and SR are operating independently, but if expedient or necessary the obtained data could be collected at one position for further data or information fusion. In the SR radar, a phased array is proposed which provides essentially better angle resolution (order or more) in comparison with the master radar within a given sector. 360 0 observation Mechanical scanning MR Synchronization channel :0 SR observation Phased array antenna Electronic scanning Figure 1: System topology An example of possible system topology is shown in Figure 1.
    [Show full text]
  • Understanding Noise Figure
    Understanding Noise Figure Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul One of the most frequently discussed forms of noise is known as Thermal Noise. Thermal noise is a random fluctuation in voltage caused by the random motion of charge carriers in any conducting medium at a temperature above absolute zero (K=273 + °Celsius). This cannot exist at absolute zero because charge carriers cannot move at absolute zero. As the name implies, the amount of the thermal noise is to imagine a simple resistor at a temperature above absolute zero. If we use a very sensitive oscilloscope probe across the resistor, we can see a very small AC noise being generated by the resistor. • The RMS voltage is proportional to the temperature of the resistor and how resistive it is. Larger resistances and higher temperatures generate more noise. The formula to find the RMS thermal noise voltage Vn of a resistor in a specified bandwidth is given by Nyquist equation: Vn = 4kTRB where: k = Boltzmann constant (1.38 x 10-23 Joules/Kelvin) T = Temperature in Kelvin (K= 273+°Celsius) (Kelvin is not referred to or typeset as a degree) R = Resistance in Ohms B = Bandwidth in Hz in which the noise is observed (RMS voltage measured across the resistor is also function of the bandwidth in which the measurement is made). As an example, a 100 kΩ resistor in 1MHz bandwidth will add noise to the circuit as follows: -23 3 6 ½ Vn = (4*1.38*10 *300*100*10 *1*10 ) = 40.7 μV RMS • Low impedances are desirable in low noise circuits.
    [Show full text]