1 Theorizing Teaching Practices in Mathematical Modeling Contexts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Following Are Unofficial Observations Taken During the Past 36 Hours for the Storm That Has Been Affecting Our Region
THE FOLLOWING ARE UNOFFICIAL OBSERVATIONS TAKEN DURING THE PAST 36 HOURS FOR THE STORM THAT HAS BEEN AFFECTING OUR REGION. APPRECIATION IS EXTENDED TO THOSE WHO PROVIDED REPORTS. THIS SUMMARY IS ALSO AVAILABLE ON OUR HOME PAGE AT WEATHER.GOV/BLACKSBURG ********************STORM TOTAL SNOWFALL******************** LOCATION STORM TOTAL TIME/DATE COMMENTS SNOWFALL OF /INCHES/ MEASUREMENT NORTH CAROLINA ...ALLEGHANY COUNTY... SPARTA 5.0 829 AM 2/15 TRAINED SPOTTER 4 SSE SPARTA 4.0 946 AM 2/15 TRAINED SPOTTER ENNICE 4.0 945 AM 2/15 PUBLIC ...ASHE COUNTY... 3 SSE FLEETWOOD 7.0 700 AM 2/15 COCORAHS 6 NW LANSING 6.0 930 AM 2/15 COCORAHS CRUMPLER 5.5 947 AM 2/15 PUBLIC TODD 5.0 1202 PM 2/15 MIXED WITH SLEET 3 SW CRESTON 4.5 915 AM 2/15 COCORAHS 1 ESE WEST JEFFERSON 4.1 700 AM 2/16 COCORAHS GLENDALE SPRINGS 4.0 1247 PM 2/15 PUBLIC ...CASWELL COUNTY... 1 ENE TOPNOT 2.1 747 AM 2/15 LIQ EQUIV 0.20 6 SSE MILTON 1.5 730 AM 2/15 COCORAHS 2 NNE CAMP SPRINGS 1.5 1100 PM 2/14 TRAINED SPOTTER 2 SW YANCEYVILLE 1.0 700 AM 2/15 COCORAHS ...ROCKINGHAM COUNTY... EDEN 3.0 334 PM 2/15 MIXED WITH SLEET 3 NNW REIDSVILLE 2.0 922 AM 2/16 CO-OP OBSERVER 2 S EDEN 1.4 917 AM 2/16 CO-OP OBSERVER ...STOKES COUNTY... SANDY RIDGE 3.0 720 PM 2/15 PUBLIC KING 2.1 923 AM 2/16 CO-OP OBSERVER 3 ENE WESTFIELD 2.0 1247 PM 2/15 PUBLIC 2 WSW FRANCISCO 2.0 826 AM 2/15 TRAINED SPOTTER DANBURY 1.7 916 AM 2/16 CO-OP OBSERVER ...SURRY COUNTY.. -

Visitors Parents and Other Visitors Are ALWAYS Welcome at Israel
Visitors Parents and other visitors are ALWAYS welcome at Israel Putnam. During school hours, all visitors are asked to enter at the main entrance (facing the bus loop), and report to the office so that we know who is in the building at all times. Your cooperation will help support a secure environment for our children. School Hours Grades 1 to 5 Please plan to have your child at school between 8:30 and 8:50. Supervision is provided for students after 8:30. No student should be dropped off at school before 8:30, unless your child is participating in a planned activity. Our hours are as follows: Regular Day Early Dismissal 8:50 - First Bell 9:00 - Late Bell 3:15 - Dismissal 1:20 - Dismissal Morning Kindergarten Please plan to have your child at school between 8:30 and 8:50. Our hours are as follows: Regular Day Early Dismissal 8:50 - First Bell 9:00 - Late Bell 11:45 - Dismissal 11:07 - Dismissal Afternoon Kindergarten Please plan to bring your child to school between 12:20 and 12:30. Our hours are as follows: Regular Day Early Dismissal 12:30 - Students Enter 11:12 Students Enter 3:15 - Dismissal 1:20 Dismissal Step Up to Safety In order to provide for your child's safety while entering in the morning and at afternoon dismissal time, we ask your cooperation. When dropping your child off, please DO... DO NOT... drop your child off after 8:30 drop your child off before 8:30. There will be NO supervision. -

104494 FB MG Text 125-232.Id2
COUGAR RADIO-TV NETWORK THE COUGAR SPORTS RADIO NETWORK 2004 OUTLLOK Cougar football games are broadcast live on the radio throughout the Pacific THE COUGAR SPORTS NETWORK Northwest via The Cougar Sports Radio Network. The 27-station network - one of (Subject to Change) the largest in the Pac-10 - reaches from British Columbia to Nevada and can be heard Location Station Frequency worldwide via the internet. Aberdeen KXRO 1320 AM The KXLY Broadcast Group produces The Cougar Sports Network, which also Bellingham KPUG 1170 AM features radio coverage of WSU men’s basketball, baseball, women’s basketball and Boise, Idaho KCID 1490 AM women’s volleyball, and 30-minute coaches show in the fall and winter seasons. Centralia KELA 1470 AM Cougar football broadcasts begin an hour before kick-off, carry through the game and conclude with post-game interviews with players and coaches and a live call-in Clarkston KCLK 1430 AM 2004 OUTLOOK talk show. Colfax KCLX 1450 AM KXLY, which began a five-year partnership with the Cougars in 2001, also publishes Colville KCVL 1240 AM Crimson & Gray Magazine, the official game-day publication of Cougar football and Everett KRKO 1380 AM WSU COACHES basketball. Grand Coulee KEYG 1490 AM Las Vegas, Nev. KLAV 1230 AM Longview KBAM 1270 AM Moscow, Idaho KZFN 106.1 FM Moscow, Idaho KRPL 1400 AM Moses Lake KBSN 1470 AM Mount Vernon KAPS 660 AM Olympia KGY 96.9 FM Omak KNCW 92.7 FM WSU COACHES Portland, Oregon KFXX 1080 AM Prosser/Sunnyside KZXR 1310 AM Robertson Walden Nameck Quincy KWNC 1370 AM PROFILES PLAYER Seattle KYCW 1090 AM THE BROADCAST TEAM Spokane KXLY 920 AM Bob Robertson Sr. -

The Mountain View Inn!
Welcome to the Mountain View Inn! On behalf of the 75th ABW, the 75th Force Support Squadron, and the Mountain View Inn Staff, welcome to Hill Air Force Base, Headquarters for the Ogden Air Logistics Center. We are honored to have you as our guest and sincerely hope your visit to Hill Air Force Base and the Layton/Salt Lake City area is an exceptional one. Please take a few minutes to review the contents of this book to discover the outstanding services available at both Hill Air Force Base and the surrounding area. If there is anything we can do to make your visit more comfortable, or if you have any suggestions on how we can improve our service, please fill out a Customer Comment Card located in your room or at our Guest Reception Desk. The Mountain View Inn is a recipient of both the prestigious Air Force Material Command Gold Key Award and the Air Force Innkeeper Award. We are truly dedicated to providing quality service to you, our valued guest, and are available 24 hours a day to assist you and make your stay a memorable one. The Mountain View Inn team of professionals wishes you a pleasant stay and a safe journey. We look forward to serving you and hope to see you again in the future! Melissa L. Edwards Lodging Manager 801-777-1844 EXT 2560 Welcome Valued Guest! We have provided you with a few complimentary items to get you through your first night’s stay. Feel free to ask any Lodging team member if you need any of these items replenished. -

EE 321 AM Radio Stations in Spokane Area Fall 2017
EE 321 AM Radio Stations in Spokane Area Fall 2017 Conventional amplitude modulation (AM) radio stations use carrier frequencies spaced 10 kHz apart, over the range of 535 kHz to 1605 kHz. Demodulation occurs by frequency shifting the carrier down to the intermediate frequency (IF) of 455 kHz, and passing the signal through a fixed narrow-band filter with bandwidth 10 kHz, centered at 455 kHz. The ideal frequency response characteristic is the “brick-wall” bandpass filter shown below. The 17 AM radio stations listed below are in the greater Spokane area. Note that two have the same carrier frequency (KOFE at 1240 AM in St. Maries, ID and KCVL at 1240 AM in Colville, WA) with one other station adjacent in frequency (KSBN at 1230 in Spokane, WA). What is the topography of the area between these three locations? Distance from Carrier Callsign Format Spokane City of License 590 AM KQNT Talk 8.5 miles Spokane, WA 630 AM KTRW 4.8 miles Opportunity, WA Airway Heights, 700 AM KXLX Sports 4.8 miles WA 790 AM KJRB Sports 11.9 miles Spokane, WA 840 AM KMAX News/Talk 52.6 miles Colfax, WA 920 AM KXLY Talk 4.8 miles Spokane, WA 970 AM KTTO 4.5 miles Spokane, WA Adult 1050 AM KEYF Standards 5.1 miles Dishman, WA 1080 AM KVNI Oldies 32.4 miles Coeur d'Alene, ID 1230 AM KSBN 1.1 miles Spokane, WA 1240 AM KOFE 47.1 miles St. Maries, ID 1240 AM KCVL Country 62.9 miles Colville, WA 1280 AM KZFS Talk 5.1 miles Spokane, WA 1330 AM KMBI Religious 5.3 miles Spokane, WA 1400 AM KSPT 59.3 miles Sandpoint, ID 1450 AM KCLX 52.6 miles Colfax, WA 1510 AM KGA Sports 11.9 miles Spokane, WA There are 11 AM radio stations within 12 miles of Spokane, with carrier frequencies 590, 630, 700, 790, 920, 970, 1050, 1230, 1280, 1330, and 1510 kHz. -

Stations Monitored
Stations Monitored 10/01/2019 Format Call Letters Market Station Name Adult Contemporary WHBC-FM AKRON, OH MIX 94.1 Adult Contemporary WKDD-FM AKRON, OH 98.1 WKDD Adult Contemporary WRVE-FM ALBANY-SCHENECTADY-TROY, NY 99.5 THE RIVER Adult Contemporary WYJB-FM ALBANY-SCHENECTADY-TROY, NY B95.5 Adult Contemporary KDRF-FM ALBUQUERQUE, NM 103.3 eD FM Adult Contemporary KMGA-FM ALBUQUERQUE, NM 99.5 MAGIC FM Adult Contemporary KPEK-FM ALBUQUERQUE, NM 100.3 THE PEAK Adult Contemporary WLEV-FM ALLENTOWN-BETHLEHEM, PA 100.7 WLEV Adult Contemporary KMVN-FM ANCHORAGE, AK MOViN 105.7 Adult Contemporary KMXS-FM ANCHORAGE, AK MIX 103.1 Adult Contemporary WOXL-FS ASHEVILLE, NC MIX 96.5 Adult Contemporary WSB-FM ATLANTA, GA B98.5 Adult Contemporary WSTR-FM ATLANTA, GA STAR 94.1 Adult Contemporary WFPG-FM ATLANTIC CITY-CAPE MAY, NJ LITE ROCK 96.9 Adult Contemporary WSJO-FM ATLANTIC CITY-CAPE MAY, NJ SOJO 104.9 Adult Contemporary KAMX-FM AUSTIN, TX MIX 94.7 Adult Contemporary KBPA-FM AUSTIN, TX 103.5 BOB FM Adult Contemporary KKMJ-FM AUSTIN, TX MAJIC 95.5 Adult Contemporary WLIF-FM BALTIMORE, MD TODAY'S 101.9 Adult Contemporary WQSR-FM BALTIMORE, MD 102.7 JACK FM Adult Contemporary WWMX-FM BALTIMORE, MD MIX 106.5 Adult Contemporary KRVE-FM BATON ROUGE, LA 96.1 THE RIVER Adult Contemporary WMJY-FS BILOXI-GULFPORT-PASCAGOULA, MS MAGIC 93.7 Adult Contemporary WMJJ-FM BIRMINGHAM, AL MAGIC 96 Adult Contemporary KCIX-FM BOISE, ID MIX 106 Adult Contemporary KXLT-FM BOISE, ID LITE 107.9 Adult Contemporary WMJX-FM BOSTON, MA MAGIC 106.7 Adult Contemporary WWBX-FM -
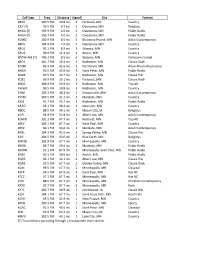
Broadcast Radio
Call Sign Freq. Distance Signal City Format KBGY 107.5 FM 10.8 mi. 5 Faribault, MN Country KJLY (T) 93.5 FM 0.7 mi. 5 Owatonna, MN Religious KNGA (T) 103.9 FM 4.0 mi. 5 Owatonna, MN Public Radio KNGA (T) 105.7 FM 4.0 mi. 5 Owatonna, MN Public Radio KOWZ 100.9 FM 8.5 mi. 5 Blooming Prairie, MN Adult Contemporary KRFO 104.9 FM 2.0 mi. 5 Owatonna, MN Country KRUE 92.1 FM 8.5 mi. 5 Waseca, MN Country KAUS 99.9 FM 31.4 mi. 4 Austin, MN Country KFOW-AM (T) 106.3 FM 8.5 mi. 4 Waseca, MN Unknown Format KRCH 101.7 FM 26.4 mi. 4 Rochester, MN Classic Rock KCMP 89.3 FM 42.6 mi. 3 Northfield, MN Adult Album Alternative KNGA 90.5 FM 45.6 mi. 3 Saint Peter, MN Public Radio KNXR 97.5 FM 43.7 mi. 3 Rochester, MN Classic Hits KQCL 95.9 FM 19.1 mi. 3 Faribault, MN Classic Rock KROC 106.9 FM 52.9 mi. 3 Rochester, MN Top-40 KWWK 96.5 FM 30.8 mi. 3 Rochester, MN Country KYBA 105.3 FM 38.3 mi. 3 Stewartville, MN Adult Contemporary KYSM 103.5 FM 41.2 mi. 3 Mankato, MN Country KZSE 91.7 FM 43.7 mi. 3 Rochester, MN Public Radio KATO 93.1 FM 48.2 mi. 2 New Ulm, MN Country KBDC 88.5 FM 49.1 mi. 2 Mason City, IA Religious KCPI 94.9 FM 31.8 mi. -

Academic Achievement Strategies Accounting
FOR THE MOST CURRENT CLASS LISTINGS AND TO REGISTER, GO TO WWW.CCD.EDU 11009 ....... 07C ........ MTR ....... 1-230 pm Section 07C is a learning community ART ACADEMIC ACHIEVEMENT section with a co-requisite of MAT 050- Center for Arts & Humanities STRATEGIES 07C (CRN 10725), which meets MTR CHR 307 • 303-556-2473 2:40PM-5:00PM. For more information Center for Math & Science contact a Program Advisor. This section is [G] ART 110 Art Appreciation: AH1 ....................... 3 CNF 301 • 303-556-3812 offered in a non-standard part of term. Prerequisite: Grade of C or better in CCR 092, CCR 093, Please check CCD Connect for the start CCR 094, or ENG 090 or equivalent English, Reading, AAA 109 Advanced Academic Achievement......... 3 and end dates. Note: Dropping this course and Writing assessment score placements; or equivalent Prerequisite: Minimum math, reading or English will automatically result in being dropped ACT/SAT scores. assessment score or equivalency required, or chair or from the co-requisite. 10321 ....... 001 ........ TR .......... 1015 am-1215 pm advisor permission. Corequisite: Students must co- enroll in a corresponding section of MAT 050. AAA 109 10837 ....... 002 ........ MW ........ 1230-230 pm is a structured study experience for MAT 050 students. ACCOUNTING 10608 ....... 01A ........ TR .......... 1-530 pm 11006 ....... 01C ........ MTR ....... 1120 am-1250 pm Section 01A is a 5-week accelerated Center for Career & Technical Education Section 01C is a Learning Community course. This section is offered in a non- section with a co-requisite of MAT 05001C CHR 201 • 303-556-2487 standard part of term. -

NATIONAL SHOWS – LIVE and INTERACTIVE – COAST to COAST New York • Los Angeles • Chicago • San Francisco • Philadelphia • Phoenix • +150 More!
NATIONAL SHOWS – LIVE AND INTERACTIVE – COAST TO COAST New York • Los Angeles • Chicago • San Francisco • Philadelphia • Phoenix • +150 more! Ashley Noronha Rome Correspondent Msgr. Stuart Swetland Chief Religion Correspondent JOIN THE CONVERSATION! Call our studio line at 888-914-9149 ET CT Week Days Saturday Sunday MT PT 6a 5a Morning Air® 4a 3a 7a 6a Children’s Rosary 5a 4a Morning Air® 7:30a 6:30a Morning Air® Christopher Closeup 5:30a 4:30a 8a 7a Inspiring, informative, joyful, and family-friendly conversations to start your day. Life is Worth Living 6a 5a 9a 8a Where God Weeps 7a 6a 9:30a 8:30a Word on Fire™ 7:30a 6:30a Patrick Madrid Show 10a 9a The Patrick Madrid Show Sunday Mass 8a 7a 11a 10a Your source for the latest in current events, culture trends, and contemporary issues. The Miracle Hunter® 9a 8a noon 11a The Inner Life® Inner Life® Trending 10a 9a On air spiritual direction from a rotating panel of highly experienced Catholic priests. 1p noon Go Ask Your Father™ Go Ask Your Father™ Dan Cheely Show™ 11a 10a Answers to your questions about faith and morals, doctrine and social teaching. 2p 1p Word on Fire™ noon 11a Father Simon Says™ Father Simon Says™ 2:30p 1:30p St Paul Center Presents 12:30p 11:30a Your daily bible study with Scripture readings, Word of the Day, and faith Q&A. 3p 2p 1p noon 4p 3p The Drew Mariani Show™ Drew Mariani Show™ Drew Mariani Show™ 2p 1p 5p 4p Breaking news coverage and conversation. -

2017 Media Directory
Media Contacts Katrina Thompson Director of Marketing and Communications Phone: 208.331.4738 Email: [email protected] Lorie O’Donley Content Marketing Coordinator Phone: 208.331.4858 Email: [email protected] Idaho Housing and Finance Association Phone: 855.505.4700 Social Media /idahohousing @idahohousing youtube.com/user/IDhousing bitl.y/idahohousing 2017 Directory Page 1 Page 2 Idaho Housing and Finance Association improves lives and strengthens Idaho communities by expanding housing opportunities, building self- sufficiency, and fostering economic development. This directory includes Idaho newspapers, television and radio stations, presented by location according to the regional breakdown below. PAGE REGION 1 6 REGION 2 18 REGION 3 26 REGION 4 43 REGION 5 51 REGION 6 59 We have done our best to provide a comprehensive list of Idaho’s media, but please keep in mind that the media industry can be quite fluid. When possible, the phone number and email provided are direct to the news room of the media outlet. Page 3 Page 4 REGION 1 NORTH IDAHO Coeur d’Alene, Sandpoint, Bonners Ferry Daily Newspapers Bonner County Daily Bee P.O. Box 159 / 310 Church Street Circulation : 6,200 Sandpoint, ID 83864 Phone: (208) 263-9534 Fax: (208) 263-9091 Email: [email protected] Website: www.bonnercountydailybee.com Facebook: /bonnercountydailybee Twitter: @dailybee Coeur d’Alene Press P.O. Box 7000 / 215 N. Second Street Circulation : 22,000 Coeur d’Alene, ID 83814 Phone: (208) 664-8176 Fax: (208) 664-0212 Email: [email protected] Website: www.cdapress.com Facebook: /cdapress Twitter: @cda_press Page 5 Page 6 REGION 1 REGION 1 Spokesman Review North Idaho Business Journal P.O. -

Media Directories
Media Directories Nampa Depot Photo courtesy of Jeff Harvey Region 1: North Idaho Coeur d’Alene, Sandpoint, Bonners Ferry Daily Newspapers Bonner County Daily Bee Spokesman Review P.O. Box 159 P.O. Box 2160 310 Church Street 999 W. Riverside Ave. Sandpoint, ID 83864 Spokane, WA 99210 208-263-9534 509-459-5400/800-789-0029 www.bonnercountydailybee.com www.spokesman.com [email protected] [email protected] Coeur d’Alene Press P.O. Box 7000 215 N. Second Street Coeur d’Alene, ID 83814 208-664-8176 www.cdapress.com [email protected] Non-Daily Newspapers Bonners Ferry Herald Sandpoint Reader P.O. Box 539 111 Cedar Street, Ste. 9 7183 Main Street Sandpoint, ID 83864 Bonners Ferry, ID 83805 208-265-9724 208-267-5521 www.sandpointreader.com www.bonnersferryherald.com [email protected] [email protected] The Sentinel Bonners Ferry News North Idaho College P.O. Box 1640 1000 W. Garden Ave. Bonners Ferry, ID 83805 Coeur d’Alene, ID 83814 208-295-1016 208-769-3228 www.newsbf.com www.nisentinel.com [email protected] [email protected] Shoshone News-Press North Idaho Business Journal P.O. Box 589 P.O. Box 7000 620 E. Mullan Ave. 215 N. Second Street Osburn, ID 83849 Coeur d’Alene. ID 83814 208-752-1120 208-664-0219 www.shoshonenewspress.com www.bookshelf.cdapresshost.com/nibi/ [email protected] index.html [email protected] Spokane Journal of Business 429 E. 3rd Ave. Priest River Times Spokane, WA 99202 P.O. Box 159 509-456-5257 310 Church Street www.spokanejournal.com Priest River, ID 83864 [email protected] 208-448-2431 St. -

The Death Penalty in 2013: Year End Report
! ! THE DEATH PENALTY IN 2013: YEAR END REPORT Media Coverage Summary ! DPIC’s 2013 Year End Report was released on December 19, 2013, receiving extraordinary coverage. Coverage of the report appeared in over 500 media outlets, and was notable in two important respects. First, there was an increase in the amount of news coverage and editorial board attention. Second, 2013 was the year the media reported and underscored our message that “[a] societal shift is underway,” as quoted in the New York Times. Coverage of the 2013 Year End Report included stories in the New York Times, Washington Post, USA Today, Los Angeles Times, Wall Street Journal, Time, CNN, Associated Press, Reuters and AFP, and in hundreds of other articles and editorials. Richard Dieter was interviewed on MSNBC-TV and C-SPAN’s Washington Journal. Stories also ran on NPR (two stories), CBS, ABC, NBC, and Associated Press Radio Networks. As an example of our use of new media, The Guardian (which now has web traffic inside the U.S. similar to the Washington Post and the Los Angeles Times) hosted an online chat about the report with DPIC’s Executive Director. The theme of a fundamental change in the country was echoed widely. For example, newspapers in North Carolina carried DPIC’s observation that the decline of the death penalty was not a "one-year quirk … It's indicative of some broad changes in society.” This theme was reflected in New York Times and Washington Post editorials, as well as editorials in Alabama, Delaware, Florida, Illinois, Nebraska, North Carolina, Ohio, Pennsylvania, and Texas.