Cellular Automata in Cryptographic Random Generators
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
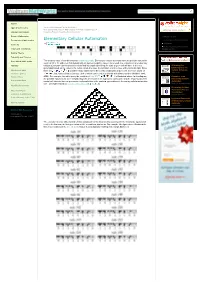
Elementary Cellular Automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations >
Search MathWorld Algebra Applied Mathematics Discrete Mathematics > Cellular Automata > Recreational Mathematics > Mathematical Art > Mathematical Images > elementary cellular automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations > Discrete Mathematics THINGS TO TRY: Foundations of Mathematics Elementary Cellular Automaton elementary cellular automaton 39th prime Geometry do the algebraic units contain History and Terminology Sqrt[2]+Sqrt[3]? Number Theory Probability and Statistics Recreational Mathematics The simplest class of one-dimensional cellular automata. Elementary cellular automata have two possible values for each cell (0 or 1), and rules that depend only on nearest neighbor values. As a result, the evolution of an elementary Topology cellular automaton can completely be described by a table specifying the state a given cell will have in the next A Strategy for generation based on the value of the cell to its left, the value the cell itself, and the value of the cell to its right. Since Exploring k=2, r=2 Alphabetical Index there are possible binary states for the three cells neighboring a given cell, there are a total of Cellular Automata John Kiehl Interactive Entries elementary cellular automata, each of which can be indexed with an 8-bit binary number (Wolfram 1983, Random Entry 2002). For example, the table giving the evolution of rule 30 ( ) is illustrated above. In this diagram, Dynamics of an the possible values of the three neighboring cells are shown in the top row of each panel, and the resulting value the Elementary Cellular New in MathWorld central cell takes in the next generation is shown below in the center. generations of elementary cellular automaton Automaton rule are implemented as CellularAutomaton[r, 1 , 0 , n]. -

Wolfram's Classification and Computation in Cellular Automata
Wolfram's Classification and Computation in Cellular Automata Classes III and IV Genaro J. Mart´ınez1, Juan C. Seck-Tuoh-Mora2, and Hector Zenil3 1 Unconventional Computing Center, Bristol Institute of Technology, University of the West of England, Bristol, UK. Departamento de Ciencias e Ingenier´ıade la Computaci´on,Escuela Superior de C´omputo,Instituto Polit´ecnicoNacional, M´exico. [email protected] 2 Centro de Investigaci´onAvanzada en Ingenier´ıaIndustrial Universidad Aut´onomadel Estado de Hidalgo, M´exico. [email protected] 3 Behavioural and Evolutionary Theory Lab Department of Computer Science, University of Sheffield, UK. [email protected] Abstract We conduct a brief survey on Wolfram's classification, in particular related to the computing capabilities of Cellular Automata (CA) in Wol- fram's classes III and IV. We formulate and shed light on the question of whether Class III systems are capable of Turing universality or may turn out to be \too hot" in practice to be controlled and programmed. We show that systems in Class III are indeed capable of computation and that there is no reason to believe that they are unable, in principle, to reach Turing-completness. Keywords: cellular automata, universality, unconventional computing, complexity, gliders, attractors, Mean field theory, information theory, compressibility. arXiv:1208.2456v2 [nlin.CG] 29 Aug 2012 1 Wolfram's classification of Cellular Automata A comment in Wolfram's A New Kind of Science gestures toward the first dif- ficult problem we will tackle (ANKOS) (page 235): trying to predict detailed properties of a particular cellular automaton, it was often enough just to know what class the cellular automaton was in. -

Complex Systems 530 2/9/21 What Is a Cellular Automaton?
Lecture 5: Introduction to Cellular Automata Complex Systems 530 2/9/21 What is a cellular automaton? • Automata: “a theoretical machine that changes its internal state based on inputs and its previous state” (usually finite and discrete) - Sayama p.185 • Cellular automata: automata on a regular spatial grid, that update state based on their neighbors’ states, using a state transition function • Usually synchronous, discrete in time & space, often deterministic (but not always!) 11.1. DEFINITION OF CELLULAR AUTOMATA 187 Configulation Configulation at time t at time t+1 Neighborhood T L C R B State set State-transition function C TR B L C TR B L C TR B L C TR B L { , } Figure 11.1: Schematic illustration of how cellular automata work. Sayama p. 187 (Chp. 11) Figure 11.2: Examples of neighborhoods often used for two-dimensional CA. Left: von Neumann neighborhood. Right: Moore neighborhood. Cellular automata • Cellular automata can generate highly nonlinear, even seemingly random behavior • Much more complexity than one might expect from simple rules—emergent behavior • To explore this, let’s start with an even ‘simpler’ type of cellular automata—1-dimensional CA and some of the classic work of Stephen Wolfram 1-dimensional CA • We can think of our grid as a string or line of cells • Finite sequence - 1 row of cells, so everyone has 2 neighbors except the end points • Choose how to interpret the ends (lack of neighbors or fixed states at ends) • Ring - all cells have 2 neighbors • Infinite sequence - an infinite number of cells arranged in a row 52 Chapter 6. -

FINITE-WIDTH ELEMENTARY CELLULAR AUTOMATA 1. Introduction Stephen Wolfram's a New Kind of Science Explores Elementary Cellular
FINITE-WIDTH ELEMENTARY CELLULAR AUTOMATA IAN COLEMAN Abstract. This paper is an empirical study of eight-wide elementary cellu- lar automata motivated by Stephen Wolfram's conjecture about widespread universality in regular elementary cellular automata. Through examples, the concepts of equivalence, reversibility, and additivity in elementary cellular au- tomata are explored. In addition, we will view finite-width cellular automata in the context of finite-size state transition diagrams and develop foundational results about the behavior of finite-width elementary cellular automata. 1. Introduction Stephen Wolfram's A New Kind of Science explores elementary cellular au- tomata and universality in simple computational systems [3]. In 1985, Wolfram conjectured that an elementary cellular automaton could be Turing complete, thus capable of universal computation. At the turn of the century, Matthew Cook pub- lished a proof confirming that a particular cellular automaton, known as \Rule 110," was universal [1]. Wolfram currently conjectures that universality in non-trivial cel- lular automata (and other simple systems) is likely to be extremely common. This paper, in addition to an outline of Wolfram's basic work, is an empirical study seeking to add information and insight to the exploration of elementary cellular automata. Elementary cellular automata have become relevant given Wolfram's develop- ment of the Principle of Computational Equivalence. From Wolfram, the Principle of Computational Equivalence states that \almost all processes that are not ob- viously simple can be viewed as computations of equivalent sophistication [3, p. 5 , 716-717]." Wolfram's MathWorld explains further that \the principle of com- putational equivalence says that systems found in the natural world can perform computations up to a maximal (\universal") level of computational power, and that most systems do in fact attain this maximal level of computational power. -

Compression-Based Investigation of the Dynamical Properties of Cellular Automata and Other Systems
Compression-based investigation of the dynamical properties of cellular automata and other systems Hector Zenil Laboratoire d'Informatique Fondamentale de Lille (USTL/CNRS) and Institut d'Histoire et de Philosophie des Sciences et des Techniques (CNRS/Paris 1/ENS Ulm) [email protected] October 19th., 2009 Abstract A method for studying the qualitative dynamical properties of abstract computing machines based on the approximation of their program-size complexity using a general lossless compression algorithm is presented. It is shown that the compression- based approach classifies cellular automata (CA) into clusters according to their heuristic behavior, with these clusters showing a correspondence with Wolfram's main classes of CA behavior. A compression based method to estimate a character- istic exponent to detect phase transitions and measure the resiliency or sensitivity of a system to its initial conditions is also proposed, constituting a compression-based framework for investigating the dynamical properties of cellular automata and other systems. Keywords: cellular automata classification, Wolfram's four classes, phase transition detection, program-size complexity, compression-based clustering, non-linear dynamics, Lyapunov characteristic exponents. 2 ClusteringCAComplexSystems-Zenil.nb Introduction Previous investigations of the dynamical properties of cellular automata have involved compression in one form or another. In this paper, we take the direct approach, experimentally studying the relationship between properties of dynamics and their compression. Cellular automata were first introduced by J. von Neumann[16] as a mathematical model for biological self-replication phenomena, and have played a basic role in understanding and explaining various complex physical, social, chemical, and biological phenomena. -

Part III Complex Systems, Chaos and Fractals
Part III Complex Systems, Chaos and Fractals Chapter 6 Cellular Automata 6.1 Why Study Cellular Automata? The contents of the lecture has been so far – and despite the numerous applica- tions that followed – admittedly rather formal. In contrast, the present chapter on Cellular Automata, building on the theoretical material introduced so far, offers an exciting and visually enthralling way into the theory of complex systems. Complex systems are systems composed of many interconnected simple parts, out of which highly ordered behaviors emerge. Interestingly, complex systems can be found almost everywhere – not only in formal systems such as cellular automata, but also in nature, society and science. Its study has become a very active interdisciplinary field of modern science. This chapter starts by investigating what happens when several finite state au- tomata (the abstract machines we’ve learned to known in Chapter 3) are assembled into an array. Even though we will only study systems being entirely determinis- tic, we are in for big surprises! We’ll discover that already in such systems com- posed of trivially simple elements, self-organization, fractals, chaos and complex behaviors can be observed. 6-1 6-2 CHAPTER 6. CELLULAR AUTOMATA 6.2 Definition of Cellular Automata Cell Lattice Cellular Automata (CA) are mathematical models in which space and time are discrete. Time proceeds in steps and space is represented as a lattice or array of cells (see Figure 6.1). The dimension of this lattice is referred to as the dimension of the CA. Each cell in a particular state that may change over time. -

Code 1599 Cellular Automaton New Patterns
Code 1599 Cellular Automaton New Patterns Minjie Lei University of Michigan Code 1599 is a cellular automaton rule that produces complex patterns that resemble the phenomenon of free will under simple initial condi- tions. However, by expanding the range of initial conditions considered to include complex backgrounds, we find that code 1599 can produce patterns that are entirely different from its ordinary structure, but simi- lar or even structurally identical to some elementary cellular automata rules. 1. Code 1599 Introduction Code 1599 was first introduced by Stephen Wolfram in 1983 [1]. It is a three-color totalistic cellular automaton rule, which means each cell has only three possible colors and depends only on the total sum of the values of its neighboring cells. Figure 1 shows the rule plot for code 1599. Figure 1. Rule plot for code 1599. The plot shows that each color is given a number, and the color number of the next cell is determined by the sum of the color numbers of the previous cell and its neighboring cells. As simple as the rule seems, the patterns produced by code 1599 with simple initial conditions can be very interesting and distinct from other cellular automata rules. The typical code 1599 behavior as dis- cussed in Wolfram’s paper and subsequent discussions about the rule is shown in Figure 2. We can see that the rule evolves into a complex tree-like structure. Yet what makes code 1599 even more fascinating is that for many ini- tial conditions if not all, after very large steps, the complex behavior turns into simple repetitive patterns as shown in Figure 3. -

1-Dimensional Cellular Automata
1-Dimensional Cellular Automata Math Circles 2018 University of Waterloo At first, Zoink was alone. But Budlings have the special power of friendification! I Every Budling can create Budlings beside him. I But if a Budling gets surrounded, he dies! Planet Friendship This is Zoink. He is a Budling from Planet Friendship. I Every Budling can create Budlings beside him. I But if a Budling gets surrounded, he dies! Planet Friendship This is Zoink. He is a Budling from Planet Friendship. At first, Zoink was alone. But Budlings have the special power of friendification! I But if a Budling gets surrounded, he dies! Planet Friendship This is Zoink. He is a Budling from Planet Friendship. At first, Zoink was alone. But Budlings have the special power of friendification! I Every Budling can create Budlings beside him. Planet Friendship This is Zoink. He is a Budling from Planet Friendship. At first, Zoink was alone. But Budlings have the special power of friendification! I Every Budling can create Budlings beside him. I But if a Budling gets surrounded, he dies! First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship First 16 days on Planet Friendship Birth, survival, and death The rules on Planet Friendship are very precise. -

Pseudo Random Number Generation Using Hardware Implementation of Elementary Cellular Automata
Pseudo Random Number Generation Using Hardware Implementation of Elementary Cellular Automata by William A. Schenck A Thesis Submitted in Partial Fulfillment for the Requirements for the Degree of Master of Science in Engineering Technology Middle Tennessee State University December 2016 Thesis Committee: Dr. Karim Salman (Committee Chair) Dr. Walter W. Boles (Dept. Chair) Dr. Saleh M. Sbenaty (Committee Member) To my parents for their love and support. ii ACKNOWLEDGEMENTS I would like to thank Dr. Karim Salman for his invaluable guidance without which this project would have never happened. iii ABSTRACT Stephen Wolfram suggested cellular automata may be a good candidate for generating suitable encrypted data. His work recommends that rule thirty was good enough for data encryption. The production of strong data encryption is the goal of anyone who desires the means of transmitting secure messages. Studies worldwide has generated numerous volumes of research. However, these studies are based on the use of computational machinery to produce these results. This project goes beyond the computational method of pseudo-random number generation. Through the use of VHDL, a working pseudo-random number generator can be designed and programmed into a FPGA device. A pseudo-random number generator (based around elementary cellular automation) has been implemented and it was installed into a FPGA device. This working device produced results that matched the computational methods of a similar pseudo- random number generator. iv TABLE OF CONTENTS Page -

Elementary Cellular Automata with Memory
letourneau_pdf.nb 1 Elementary Cellular Automata with Memory Paul-Jean Letourneau Department of Physics, University of Calgary Elementary Cellular Automata (ECA) In order to explain how an Elementary Cellular Automaton with Memory works, let me put it in the context of an ECA. In an ECA, one has a row of cells, each either black or white. Each cell is updated in parallel according to a simple rule that states what the new color of the cell should be, depending on its current color and that of its left and right neighbors. There are 256 such rules, but only 88 remain after removing cases that are equivalent with respect to left-right reflection and black-white inversion. Elementary Cellular Automata cont'd Although all the cells in a row are updated in parallel in a CA, this animation shows each cell being updated one at a time. The red border shows the cell being updated, along with its neighborhood above it. In the rule table at the bottom, the rule case that's being used for that particular cell is also highlighted in red. letourneau_pdf.nb 2 Elementary Cellular Automata with Memory Here is how I propose to incorporate memory into an ECA. Now the value of the centre cell in the neighborhood will be referenced from a step in the past. Here is an example where the value of the centre cell is taken from two (2) time steps into the past. The "memory" here is therefore 2. letourneau_pdf.nb 3 Notice that we're still using the same rule table. -

Modelling with Cellular Automata
Modelling with cellular automata Modelling with cellular automata Shan He School for Computational Science University of Birmingham Module 06-23836: Computational Modelling with MATLAB Modelling with cellular automata Outline Outline of Topics Concepts about cellular automata Elementary Cellular Automaton Langton's ant Game of life CA for Lotka-Volterra model Conclusion Modelling with cellular automata Concepts about cellular automata What are cellular automata? I cellular automaton: a discrete model consists of a regular grid of cells, each in one of a finite number of states, such as \On" and “Off”. I The grid is usually in 2D, but can be in any finite number of dimensions. I The cells evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells. I Originated from von Neumann, populated in 70s' by John Conway's Game of Life, further researched by Stephen Wolfram I Can be seen as the simplest agent-based models Modelling with cellular automata Concepts about cellular automata Why CA are important? I The best tool to model and study complex system, because: I They are simple; I The mechanisms are completely known; I They can do just about anything I They might help us understand our universe: is the universe a cellular automaton? I They have lots of applications, e.g., random number generator. Modelling with cellular automata Concepts about cellular automata Some CA based biological models I Pattern formation in biology, e.g., Conus textile I Modelling cell interactions: brain tumor growth. Modelling with cellular automata Elementary Cellular Automaton Elementary Cellular Automaton I The simplest: One dimensional; I Two possible states per cell: `0' and `1'; I A cell's neighbors defined to be the adjacent cells on either side of it. -

Collective Behavior Modeling on the Base of Cellular Emotional Automate
E3S Web of Conferences 210, 02002 (2020) https://doi.org/10.1051/e3sconf/202021002002 ITSE-2020 Digitalization of management: collective behavior modeling on the base of cellular emotional automate Vladimir Meshkov1, Natalia Kochkovaya1,*, Irina Usova1, and Liudmila Stolyar1 1Institute of Technologies (branch) of DSTU in Volgodonsk, 347386, Mira avenue, 16, Volgodonsk, Rostov region, Russia Abstract. The paper considers the author's approach to digitalization of management of the emotional state of collectives of individuals. Collective models are built on the basis of the «cellular emotional automatе» proposed by the authors. The possibility of using the standard rules for cellular automatе in modeling the emotional behavior of collectives is shown. The proposed approach can be attributed to artificial intelligence technologies. 1 Introduction One of the main tasks of introducing artificial intelligence technologies into modern life is the task of digitalizing the management of both artificial and natural systems. So, today there are many attempts to use a wide variety of natural computing models in the digitalization of management not only for technical systems, but also for human collectives. The classic sections of natural computing at the moment are: genetic algorithms, cellular automata, artificial neural networks [1-7]. In this work, we will focus on models based on cellular automatе. Cellular automatеs are a discrete system that changes its state step by step using transition rules. We will consider the possibility of constructing «emotional» № cellular automate as models of individuals and models of collectives. Let's consider the models of collective behavior from the point of view of natural computing. What is a collective? How is it organized? On what principles can a team be organized? This is either a hierarchy of random interactions, or object modeling, attribute models, etc.